
Learning Probabilistic Models for Recognizing Faces
under Pose Variations
M. Saquib Sarfraz and Olaf Hellwich
Computer vision and Remote Sensing, Berlin university of Technology
Sekr. FR-3-1, Franklinstr. 28/29, Berlin, Germany
Abstract. Recognizing a face from a novel view point poses major challenges
for automatic face recognition. Recent methods address this problem by trying
to model the subject specific appearance change across pose. For this, however,
almost all of the existing methods require a perfect alignment between a gallery
and a probe image. In this paper we present a pose invariant face recognition
method centered on modeling joint appearance of gallery and probe images
across pose in a probabilistic framework. We propose novel extensions in this
direction by introducing to use a more robust feature description as opposed to
pixel-based appearances. Using such features we put forward to synthesize the
non-frontal views to frontal. Furthermore, using local kernel density estimation,
instead of commonly used normal density assumption, is suggested to derive
the prior models. Our method does not require any strict alignment between
gallery and probe images which makes it particularly attractive as compared to
the existing state of the art methods. Improved recognition across a wide range
of poses has been achieved using these extensions.
1 Introduction
Recent approaches to face recognition are able to achieve very low error rates in the
context of frontal faces. A more realistic and challenging task is to recognize a face at
a non-frontal view when only one (e.g. frontal) training image is available. Pose
variation in terms of pixel appearance, is highly non-linear in 2D, but linear in 3D.
Notable work such as [2] shows good results for recognition in the presence of pose
mismatch. A drawback of this, however, is the requirement of multiple gallery images
or depth information of the subject. From a practical stand point, we have at most a
single 2D gallery image per subject, and thus 2D appearance based methods have to
be further investigated for view independent recognition.
In the context of 2D appearance based methods, approaches addressing pose
variation can be categorized into two main bodies of work. Multi-view face
recognition is a direct extension of frontal face recognition in which the algorithms
require gallery images of every subject at every pose [1]. In this context, to handle the
problem of one training example, recent research direction has been to use specialized
synthesis techniques to generate a given face at all other views and then perform
conventional multi-view recognition[7][4]. Such synthesis techniques, however,
suffers from severe artifacts and are not sufficient to preserve the identity of a person
in general.
Saquib Sarfraz M. and Hellwich O. (2008).
Learning Probabilistic Models for Recognizing Faces under Pose Variations.
In Image Mining Theory and Applications, pages 122-132
DOI: 10.5220/0002341001220132
Copyright
c
SciTePress

The other very recent line of work has been to directly model the local appearance
change, due to pose, across same subjects and among different subjects. Differences
exist among different methods, in how these models are built, but the goal of all is
same i.e. trying to approximate the joint probability of a gallery and probe face across
different pose [5][11][17]. Such an approach is particularly attractive in that it does
not depend on error prone synthesis and it also automatically solves the one training
image problem in a principled way as these appearance models can be learned
effectively from an offline database of representative faces. Another benefit of such a
line of work is that adding a new person’s image in the database does not require
training the models again. We note, however, almost all of these methods proposed in
literature until now intrinsically assume a perfect alignment between a gallery and
probe face in each pose. This alignment is needed, because, otherwise, in current
appearance-based methods it is not possible to discern between the change of
appearance due to pose and change of appearance due to the local movement of facial
parts across pose.
In this contribution, we introduce novel extensions in this line of work and propose
to build models on features which are robust against misalignments and thus do not
require the facial landmarks to be detected as such. Our approach, briefly, is to learn
probabilistic models describing the approximated joint probability distribution of a
gallery and probe image at different poses. Since we address the problem where at
most one training image (e.g. frontal) is available, we learn such models by explicitly
modeling facial appearance change between frontal and other views when identity of
a person is same and when it is different across pose. This is done by computing
similarities between extracted features of faces at frontal and all other views. The
distribution of these similarities is then used to obtain the likelihood functions of the
form.
gp
p
(I ,I |C ), C {S,D}∈
(1)
‘C’ refers to classes where the gallery ‘I
g
’
and probe ‘I
p
’
images are similar (S) and
dissimilar (D) in terms of subject identity. For this purpose an independent generic set
of faces, at views we want to model, is used for offline training.
A contribution is made in this paper towards improved recognition performance
across pose without the need of properly aligning gallery and probe images. To
achieve this, we propose to use an extension of SIFT features [12], that are
specifically adapted for the purpose of face recognition in this work. This feature
description captures the whole appearance of a face in a rotation and scale invariant
manner, and is shown robust with regards to variation of facial appearance due to
localization problems [14]. Furthermore, we propose to synthesize these features at
non-frontal views to frontal by using multivariate regression techniques. The benefit
of this in recognition performance is demonstrated empirically. To approximate the
likelihood functions in equation 1, we propose to use local kernel density estimation
for deriving models as opposed to commonly used Gaussian Model.
123123

2 Modeling whole Face Appearance Change across Pose
Our approach is to extract whole appearance of the face in a manner which is robust
against misalignment due to localization. For this we use feature description [12] that
is slightly adapted for the purpose of face recognition in this work. It models the local
parts of the face and combines them into a global description. We then synthesize
features at non-frontal views to frontal. Computing similarities using these features
between frontal and other poses provides us with prior distribution for each pose.
These distributions are then modeled using a variant of local kernel density estimator
instead of commonly assumed Gaussian model.
We show, in section 2.4, that deriving model using local kernel density results in a
better fit than assumed Gaussian model. The effectiveness of our method is
demonstrated using CMU Pose, Illumination and Expression (PIE) database [15].
2.1 Facial Database
We use CMU PIE database for training and testing of our models. The PIE database
consists of 68 subjects imaged under 13 poses, 21 illumination conditions and 3
expression variations. We use the pose portion of this database with frontal
illumination and neutral expression in all 13 poses. Each pose is approximately 22.5
o
apart.
As depicted in figure 1, the pose varies from pose 1(frontal) to pose 9(left-
profile) with pose 5(Right-profile). Where pose 10, 11, 12 and 13 correspond to up
and down tilt of the face in corresponding poses.
Fig. 1. 13 poses covering left profile (9), frontal (1) to right profile(5), and slightly up/down tilt
in pose 10, 11, 13 and 12 of corresponding poses in 8, 1 and 4 respectively.
Images of half of the subjects are used as offline training set for training of models,
while other half are used for testing. Face windows are cropped from the database
without employing any commonly used normalization procedure. Therefore images
contain typical variations that may arise due to miss-localization like scale, part
clippings and background. All images are then resized to 128x128 pixels.
Typical variations present in the database are depicted in few of the example
images in figure 2.
124124
Fig. 2. Examples of cropped facial images depicting typical variations due to miss-localization
e.g. scale, part clipping, background etc.
Note that, since we do not employ any kind of normalization such as fixing eye
location or eye-distance, face images across pose suffer from typical misalignment.
2.2 Feature Extraction
As described earlier, commonly used facial representations are related directly to
pixel intensities and, as such, are not invariant to changes in scale, position,
orientation, brightness and contrast of a face. Since these types of transformations are
to be expected after a face detector stage, alignment by using several facial landmarks
is needed.
We propose to use a representation based on gradient location-orientation
histogram (GLOH) [12], which is more sophisticated and is specifically designed to
reduce in-class variance by providing some degree of invariance to the
aforementioned transformations. GLOH features are an extension to the descriptors
used in the scale invariant feature transform (SIFT) [9], and have been reported to
outperform other types of descriptors in object recognition tasks [12].
The extraction procedure has been slightly adapted to the task of face recognition
and will be described in the remainder of this section.
The extraction process begins with the computation of scale adaptive spatial
gradients for a given image I(x,y). These gradients are given by
t
w(x, y,t) t L(x, y;t)
xy
xy
t
∇≡ ∇
∑
(5)
where L(x,y; t) denotes the linear Gaussian scale space of I(x,y) [8] and w(x,y,t) is a
weighting, as given in equation 6.
4
t
tL(x,y;t)
xy
w(x, y,t)
4
t
tL(x,y;t)
xy
t
∇
=
∇
∑
(6)
125125

Fig. 3. (a-b) Gradient magnitudes (c) polar-grid partitions (d) 128-dimentional feature vector
(e). Example image.
The gradient magnitudes obtained for two example images (figure 3. e) are shown
in figure 3.b. The gradient image is then partitioned on a grid in polar coordinates, as
illustrated in figure 3.c. The partitions include a central region and seven radial
sectors. The radius of the central region is chosen to make the areas of all partitions
equal. Each partition is then processed to yield a histogram of gradient magnitude
over gradient orientations. The histogram for each partition has 16 bins corresponding
to orientations between 0 and 2π, and all histograms are concatenated to give the final
128 dimensional feature vector, see figure 3.d.
It should be noted that, in practice, the quality of the descriptor improves when
care is taken to minimize aliasing artifacts. The recommended measures include the
use of smooth partition boundaries as well as a soft assignment of gradient vectors to
orientation histogram bins.
2.3 Synthesizing Features at Non-Frontal Views to Frontal
It is well known that when a large number of subjects are considered, the recognition
performance of appearance-based methods deteriorates significantly. It is due to the
fact that distribution of face patterns is no longer convex as assumed by linear models.
By transforming the image in the previous section into a scale and rotation invariant
manner, we assume that there exists a certain relation between these features of
frontal and posed image that we can linearly transform. We justify this assumption by
comparing the similarity distributions estimated from non-synthesized GLOH features
and synthesized features. One simple and powerful way of relating these features is to
use the regression techniques. Let us suppose that we have the following multivariate
linear regression model, for finding relation between the feature vectors of frontal ‘I
F
’
and
any other angle I
P
.
I
F
= I
P
B
(7)
p
T
T
ββ
I1
I
p1 (1,1) (1,D)
F1
=
TT
ββ
II1
(D+1,1) (D+1,1)
F
n
n
⎡⎤⎡ ⎤
⎡
⎤
⎢⎥⎢ ⎥
⎢
⎥
⎢⎥⎢ ⎥
⎢
⎥
⎢⎥⎢ ⎥
⎢
⎥
⎢⎥⎢ ⎥
⎣
⎦
⎣⎦⎣ ⎦
r
r
K
MM MOM
rr
K
(8)
126126

Where n > D+1, with D being the dimensionality of each
F
I
u
ur
and
P
I
u
uv
. B is a pose
transformation matrix of unknown regression parameters, under the sum-of-least-
squares regression criterion, B can be found using Moor-Penrose inverse.
T-1T
PP PF
B=(I I ) I I
(9)
This transformation matrix B is found for each of the poses Ip (±22.5
o
, ±45, ±65
o
,
±90
o
) with frontal 0
o
‘I
F
’.
Given a set of a priori feature vectors (from an offline training set
1
), representing
faces at frontal ‘I
F
’ and other poses ‘I
P
’, we can thus find the relation between them.
Any incoming probe feature vector can now be transformed to its frontal counterpart
using: I
p
=I
P
· B
p
2.4 Obtaining Prior Pose Models for Recognition
We approximate the joint likelihood of a probe and gallery face as:
gp
gp pg gp
p
(I ,I |C,Ø ,Ø ) p( |C,Ø ,Ø )
γ
≅
(10)
Where ‘C’ refers to classes where the gallery ‘I
g
’
and probe ‘I
p
’
images are similar (S)
and dissimilar (D) in terms of subject identity. ‘
pg
γ
’ is the similarity between gallery
and probe image. Cosine measure is used as a similarity metric. These likelihoods for
the similar and dissimilar class are then found by modeling the distribution of
similarities of extracted features between frontal and every pose from offline training
set.
Figure 4 depicts the histograms for the prior same and different distributions of the
similarity ‘
γ
’, for gallery and probe images across a number of pose mismatches.
Note that, the more separated the two distributions are the more discriminative power
it has to tell if the two faces are of same person or not, in that particular pose. It is
clear that the discriminative power decreases as the pose moves away from frontal. As
shown in figure 4, synthesizing features to frontal dramatically improves this
discrimination ability over a wide range of poses.
In order to compute
2
pg p
p
(|S, )
γ
φ
and
pg p
p
(|D, )
γφ
, i.e. conditional probabilities
describing similarity distributions when subject identity is same(S) and when it is
different(D), these distributions must be described by some form. The most common
assumption is the Gaussian. We note, however, employing a normal density results in
a poor fit. We therefore propose to use non-parametric local kernel density estimate.
There exist various methods to automatically estimate appropriate values for the
width σ of the kernel function. In this work, we simply set σ to be the average nearest
neighbour distance: .
1
In order to make the estimation of B feasible, 4 images/subject/pose(expression & illumination variants) are considered
from the PIE database, of the same 34 training subjects, for offline set.
2
n
i
2
nn
i=1
1- 1
p ( ) = k( ), where k( )= .
N(2)
e
υ
γγ
γυ
σσ π
−
∑
(11)
127127
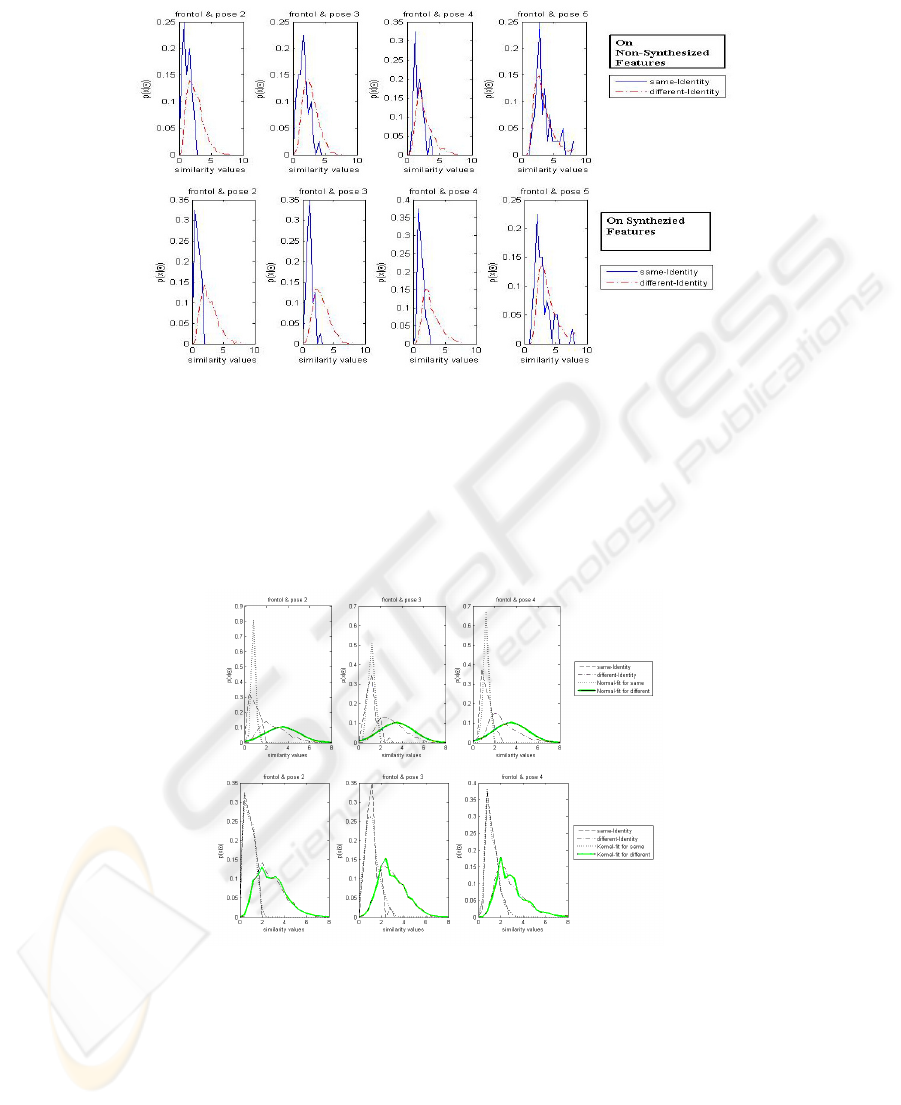
Fig. 4. x-axis denotes the similarity measure ‘γ’ and y-axis denotes the density approximation.
1
st
row depicts histograms for the same and different classes on non-synthesized features across
4 pose mismatches (see figure 1 for the approx. pose angles). 2
nd
row depicts the kind of
separation and improvement we get by using feature synthesis.
As depicted in figure 5, the kernel density estimate is a better fit, this is because the
assumption of Gaussian distribution in such scenarios is generally not fulfilled.
Kernel density estimator, on the other hand, is known to approximate arbitrary
distributions [16].
Fig. 5. 1
st
row shows fitting a normal density, 2
nd
row shows the kernel density fits on the
distribution of similarities obtained previously.
128128

3 Recognition Across Pose
Obtained likelihood estimates
pg p
p
(|S, )
γφ
and
pg p
p
(|D, )
γφ
, in the previous section,
can now be directly used to compute the posterior probability. For a probe image I
p
at
pose ‘
p
φ
’, of unknown identity, we can now decide if it is coming from the same
subject as gallery I
g
, with each of the gallery image, by using this posterior as a
match score.
Employing these likelihoods, using Bayes rule, we write:
(12)
Since the pose
p
φ
of the probe image is in general not known, we can marginalize
over it. In this case the conditional densities for similarity value
pg
γ
can be written as
(13)
(14)
Similar to the posterior defined in equation 12, we can compute the probability of
the unknown probe image coming from the same subject (given similarity
pg
γ
) as
(15)
If no other knowledge about the probe pose is given, one can assume the pose prior
P(
p
φ
) to be uniformly distributed. We, however, use the pose estimates for a given
probe face by our developed front-end pose estimation procedure [13]. Our pose
estimation system provides us with probability scores for each pose that can be used
directly as priors in equation 15. Due to a reasonably high accuracy of our pose
estimates, these probabilities can act as very strong priors and thus increase the
chances of a probe to be recognized correctly.
We compute this posterior for an unknown probe image with all of the
gallery
images and choose the identity of the gallery image with the highest score as
recognition result.
4 Recognition Results
As mentioned earlier, we use half of the subjects (34) in PIE database for training the
models described in the previous section, while images of remaining 34 subjects are
used for testing. As the gallery, the frontal images of all the 68 subjects are used. Note
that, since we do not assume any alignment between gallery and probe images,
therefore models are trained for the main 9 poses i.e. pose 1-9 in figure 1. While pose
10,11,12 and 13 corresponding to up/down tilt of the face are treated as the variations
due to misalignment for corresponding poses in the test set. All 13 poses for a subject
in the test set are therefore considered.
129129
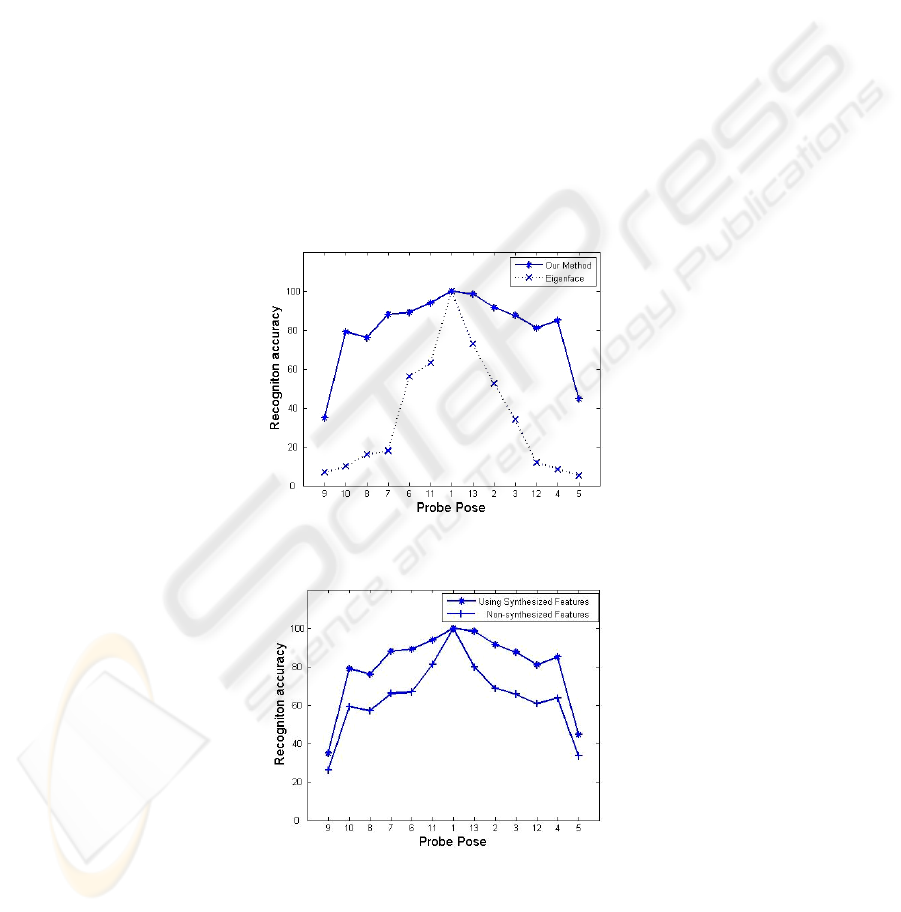
Our results show that using our method one can achieve comparable results
without putting any hard constraints on alignment of facial parts. We, however,
include the Eigenface algorithm [11] for comparison, as it is the common benchmark
in facial image processing.
For our first experiment we assume the pose of the probe images to be un-known.
We therefore use equation 15 to compute the posterior probability that probe and
gallery images come from the same subject, where we use priors P(S)<<1 and
P(D)=1-P(S).
For an incoming probe image, we extract features as described in section 2.2. In
order to synthesize these features to frontal we need to know the probe pose, as we
have to use the corresponding pose transformation matrix B. Since we use a front-end
pose estimation step, as described in previous section that provides us with the
probabilities for different possible poses, we can directly use equation 13 and 14 by
transforming the extracted feature vector of given probe to frontal for all poses. As
these pose prior probabilities P(
p
φ
) act as weights and since they are only high for the
nearest poses, therefore this does not affect the recognition performance much.
Figure 6 summarizes the recognition performance for each of the 13 poses for the
test set.
Fig. 6. Recognition results for our method and Eigenface for unknown probe pose, using
estimated pose probabilities (P(
p
φ
)) as priors.
Fig. 7. comparison between recognition results of our method for with and without feature
synthesis.
130130

For the second experiment, we compare the performance with and without feature
synthesis. Figure 7 shows the performance gain achieved by using feature synthesis.
As much as 20 % of performance gain is observed for probe poses moving away from
frontal.
Note that when a probe is at frontal (pose 1), the scores are 100% since exactly the
same images are used in the gallery for frontal pose.
5 Discussion and Conclusions
Keeping in view the preceding discussion, we can now make some comments on the
performance of our method. Note in figure 6 and 7, as the probe pose moves away
from frontal, the scores deteriorate. The larger the width at which scores remain high,
the more pose invariant the algorithm is. The scores here are presented for the more
practical situation where the probe pose angles are not assumed known a priori. In
order to cope with that, we use marginalization over probe poses. However, since we
use feature synthesis, we need strong priors for the pose angles as opposed to using
uniformly distributed assumption i.e.
p
1
P( ) =
13
φ
(for the 13 poses). As these priors act
as weights while computing the posterior in equation 15, using equal priors for every
pose results in degrading recognition performance. It is because an incoming probe
feature vector has to be transformed first to every pose using corresponding pose
transformation matrix. We have therefore used a front end pose estimation step,
which provides us with probabilities scores for each pose.
The clear advantage of using feature synthesis is shown by comparing recognition
performance with and without synthesis in figure 7. On concluding remarks, we have
presented a pose invariant face recognition method centered on modeling joint
appearance of gallery and probe images across pose in a Bayesian framework. We
have proposed novel extensions in this direction by introducing to use a more robust
feature description as opposed to pixel-based appearances. Using such features we
have proposed to synthesize the non-frontal views to frontal. The clear advantage of
this has been demonstrated experimentally. Furthermore using kernel density
estimate, instead of commonly used normal density assumption, is proposed to derive
the prior models. Our method does not require any strict alignment between gallery
and probe images and that makes it particularly attractive as compared to the existing
state of the art methods. Improved recognition across a wide range of pose has been
achieved using these extensions.
Although, we have presented results by using gallery as fixed at frontal pose, we
note that it is straight forward to use our method for any pose as gallery.
References
1. Beymer D.: Pose-invariant face recognition using real and virtual Views. M.I.T., A.I.
Technical Report No.1574, March 1996.
131131

2. Blanz V. and Vetter T.: Face recognition based on fitting a 3D morphable model. IEEE
Trans. PAMI, vol. 25, no. 9, 2003.
3. Brunelli R. and Poggio T.: Face recognition: Features versus templates. IEEE Trans.
PAMI, vol. 15, no. 10, pp. 1042–1052, 1993.
4. Gross R., Matthews I. and Baker S.: Appearance-based face recognition and light-fields.
IEEE Trans. PAMI, vol. 26, pp. 449–465, April 2004.
5. Kanade T. and Yamada A.: Multi-subregion based probabilistic approach towards pose-
invariant face recognition. in IEEE CIRA, vol. 2, pp. 954–959, 2003.
6. Kim T. and Kittler J.: Locally linear discriminant analysis for multimodally distributed
classes for face recognition with a single model image. IEEE Trans. PAMI, vol. 27, pp.
318–327, March 2005.
7. Lee H.S., Kim D.: Generating frontal view face image for pose invariant face recognition.
PR letters vol.27, No. 7, pp 747-754. 2006.
8. Lindeberg T.: Feature detection with automatic scale selection. Int. Journal of computer
vision, vol. 30 no. 2, pp 79-116, 1998.
9. Lowe D.: Distinctive image features from scale-invariant keypoints. Int. Journal of
computer vision, 2(60):91-110, 2004.
10. Martınez A. M.: Recognizing imprecisely localized, partially occluded, and expression
variant faces from a single sample per class. IEEE Trans. PAMI, vol. 24, no. 6, pp. 748–
763, 2002.
11. Moghaddam B. and Pentland A.: Probabilistic visual learning for object recognition. IEEE
Trans. PAMI, vol. 19, no. 7, pp. 696–710, 1997.
12. Mikolajczyk and Schmid C.: Performance evaluation of local descriptors. PAMI,27(10):31-
47, 2005.
13. Sarfraz M.S., Hellwich O.: Head pose estimation in face recognition across pose scenarios.
Int. conference on computer vision theory and applications VISAPP, 22-25 Jan, 2008.
14. Sarfraz M.S., Hellwich O.: Performance analysis of classifiers on face recognition", 5
th
IEEE AICS, pp. 255-264, 2006.
15. Sim T., Baker S., and Bsat S.: The CMU Pose, Illumination and Expression (PIE) database.
5
th
IEEE FG, pp. 46-51, 2002.
16. Silverman BW., Density estimation for statistics and data analysis. Chapman and Hall. 1992.
17. Vasilescu MA. O. and Terzopoulos D.: Multilinear analysis of image ensembles:
TensorFaces. ECCV, vol. 2350, pp. 447–460, 2002.
132132
