Data

Fusion by Uncertain Projective Geometry in 6DoF

Visual SLAM

Daniele Marzorati

, Matteo Matteucci

, Davide Migliore

and Domenico G. Sorrenti

Dept. Electronics and Information, Politecnico di Milano, Milano, Italy

Dept. Informatica, Sistemistica e Comunicazione, Universit

a di Milano-Bicocca, Milano, Italy

Abstract. In this paper we face the issue of fusing 3D data from different sen-

sors in a seamless way, using the unifying framework of uncertain projective ge-

ometry. Within this framework it is possible to describe, combine, and estimate

various types of geometric elements (2D and 3D points, 2D and 3D lines, and

3D planes) taking their uncertainty into account. Because of the size of the data

involved in this process, the integration process and thus the SLAM algorithm

turns out to be very slow. For this reason, in this work, we propose the use of

an R*-Tree data structure to speed up the whole process, managing in an efﬁ-

cent way both the estimated map and the 3D points clouds coming out from the

stereo camera. The experimental section shows that the use of uncertain projec-

tive geometry and the R*-Tree data structure improves the mapping and the pose

estimation.

1 Introduction

Simultaneous Localization and Mapping, SLAM hereafter, is a well-known problem in

mobile robotics since many years [1], [2], [3]. A very relevant aspect in SLAM con-

cerns the representation of the entries in the world model and the management of their

uncertainty; improper uncertainty management induces errors in robot localization and

in mapping world, which therefore suffers of geometric inconsistencies. These prevent

practical use of mobile robotics technology whenever an a priori and reliable map is not

available.

Marzorati et al. [4] demonstrated that it is possible to provide a general framework

for 3D sensor fusion, in vision based SLAM, that takes into account uncertainty in

projective geometry, providing a mean for seamless integration of several information

sources, e.g. 3D line segments, 3D planes, clouds of 3D points, etc.

The principal problem of the SLAM algorithm proposed in [4] is the lack of an

algorithm evaluation based on real data and the velocity of the algorithm (∼ 2000sec

to complete a loop of 40m), due to the size of the data involved in the process. In par-

ticular, for this last problem, it is possible to identify two bottlenecks: the ﬁrst is the

point-segment association and the second is the map-measurements data association. In

literature it is possible to ﬁnd different kind of solutions, for example, to reduce signiﬁ-

cantly these computational costs, N

uchter et al. [5, 6] proposed to use different methods,

namely point reduction, kd-trees, approximate kd-trees and cached kd-trees. Following

Marzorati D., Matteucci M., Migliore D. and G. Sorrenti D. (2008).

Data Fusion by Uncertain Projective Geometry in 6DoF Visual SLAM.

In VISAPP-Robotic Perception, pages 3-12

DOI: 10.5220/0002341600030012

 SciTePress

a parallel line, in this paper, we propose to use the R*-Tree taking into account the

uncertainty of the data involved in the process while indexing percepts.

2 Uncertain Projective Geometry

Uncertain projective geometry is a framework used to represent geometric entities and

their relationship introduced by Heuel [7, 8]. This framework is able to describe, com-

bine, and estimate various types of geometric elements (e.g. 2D and 3D points, 2D and

3D lines, 3D planes) taking uncertainty into account. These elements are represented

using homogeneous vectors, allowing the derivation of simple bilinear expressions to

represent join and intersection operators. This is obtained using only three matrices

(called construction matrix): S(·) (for 2D points and 2D lines), O(·) (for 3D lines)

and Π(·) (for 3D points and 3D planes). To get a line from two 2D points we can use

operator

l = x ∧ y = S(x)y (1)

S(x) =

∂x ∧ ∂y

∂y





0 −x

−x





, (2)

the same holds to join two 3D points into a 3D line:

L = X ∧ Y = Π(X)Y, (3)

Π(X) =

∂X ∧ ∂Y

∂Y







0 0 X

0 W

0 −Y

0 0 W

−Z

0 −Z

0 −X

−Y

0 0







. (4)

Again we can join a 3D point with a 3D line into a 3D plane:

A = X ∧ L = O(L)X, (5)

O(L) =

∂X ∧ ∂L

∂X







0 L

−L

0 L

−L

0 −L







. (6)

These construction matrices are useful tools to derive new geometric entities from

other ones, e.g. a 3D line from two 3D points, a 3D point from the intersection of two

3D lines, etc.; at the same time, being bilinear equations these operators represent the

Jacobian of the very same transformation that could be used for uncertainty propagation

in the construction process as well. Moreover, these matrices can be used to express

various geometric relations between pair of elements: incidence, identity, parallelism

and orthogonality.

Using these relations we can generate probabilistic tests to verify the relationships

between entities and to formulate a simple estimation process, to ﬁt an unknown entity

β to a set of observations ˜y constrained by a set of relationship w(˜y, β). Suppose, in

fact, to have a set of observations, described by equation:

˜y

= y

+ e

, (7)

where e

∼ N (0, Q) . To estimate the unknown entity it is possible to use a simple,

two steps, iterative algorithm:

1. Estimate the unknown entity using the relationship between the unknown and the

observations w(˜y, β) = 0 and the homogeneus constraint h(β) = 0. This can be

obtained by minimizing

Θ(˜y, β, λ, µ) = (8)

(y − ˜y)

−1

(y − ˜y) + λ

w(˜y, β) + µ

h(β),

where λ and µ are Lagrangian multipliers, respectively for the relationship and the

constraints.

2. Re-evaluate the constraints on the observations by another iterative process, updat-

ing observations by the use of the relationship, the homogeneus constraint and the

new entity estimated.

Being bilinear operators, we can estimate any new entity z, from two entities x and

y, with a simple matrix multiplication. In general we have:

z = f(x, y) = U(x)y = V (y)x, (9)

where U (x) and V (y) are, at the same time, the bilinear operators and the Jacobian of

the x and y entity respectively. Assuming entities to be uncertain, the pairs (x, Σ

(y, Σ

) and, possibly, the covariances Σ

between x and y are required for computing

the error propagation using the following simple equation:

(z, Σ

) = (10)

U(x)y, [V (y), U(x)]

¶·

(y)

(x)

¸¶

in case of independence between x and y we obtain:

(z, Σ

) =

U(x)y, U (x)Σ

y y

(x) + V (y)Σ

(y)

. (11)

Since we have estimated uncertainty, to check the geometric relationship between

two geometric entities, it is possible to use a statistical test on the distance vector d

(being this an entity deﬁned as the previous bilinear equation as well). In particular

such relationship can be assumed to hold if the hypothesis

: d = U (x)y = V (y)x = 0 (12)

cannot be rejected. Notice that the hypothesis H

can be rejected with a signiﬁcance

level of α when

T = d

−1

d > ε

= χ

1−α;n

, (13)

Obtaining the covariance matrix Σ

of d by ﬁrst order error propagation as

= U(x)Σ

(x) + V (y)Σ

(y).

In the general case Σ

may be singular; this happens if d is a n x 1 vector, r is is the

degree of freedom of the relation R and r < n. The singularity causes a problem, as

we have to invert the covariance matrix, but, at least for projective relations, it can be

guaranteed that the rank of Σ

is not less than r (see Heuel [7, 8]).

3 6DoF Visual SLAM

Our interest in the framework described in the previous section comes from the issue of

integrating 3D points, sensed by a stereo camera like the one in [9], with the 3D seg-

ments used in a previously developed algorithm for 6DoF hierarchical SLAM, sensed

basing on trinocular stereo vision, like in [10]. The algorithm uses hierarchical map

decomposition, uncertainty modeling for trinocular 3D data, and 6DoF pose represen-

tation.

In [11] we discussed in details some algorithms for data association and the impor-

tance of using a proper criterion to match features in the view with features in the map.

Usually the point-to-point distance is considered as an appropriate criterion for single

segment matching and much of the effort is devoted in ﬁnding a good association strat-

egy for dealing with the exponential complexity of ﬁnding the best match for the whole

view. In that paper we showed how a better criterion for 3D segment matching results

in a better data association almost independently from the algorithm for interpretation

tree traversal (i.e., data association algorithm).

The approach we proposed is based on a multi-criteria evaluation, for associating

segments in the view with map segments. The reason for discarding the point-to-point

criterion is mainly due to the problem of the moving-ﬁeld-of-view in the sensing sys-

tem, which turns in a moving window on the world feature(s). More precisely, the seg-

ment extrema are induced by the reduced ﬁeld of view and are not always related to real

extrema of feature in the world; when the sensing system moves it senses new extrema,

which could result in new segments, at each step; this can easily become a problem for

the classical point-to-point distance

Our proposal is of interest also for 2D-3DoF SLAM systems which groups 2D data points into

2D lines, because this moving-ﬁeld-of-view issue applies there too.

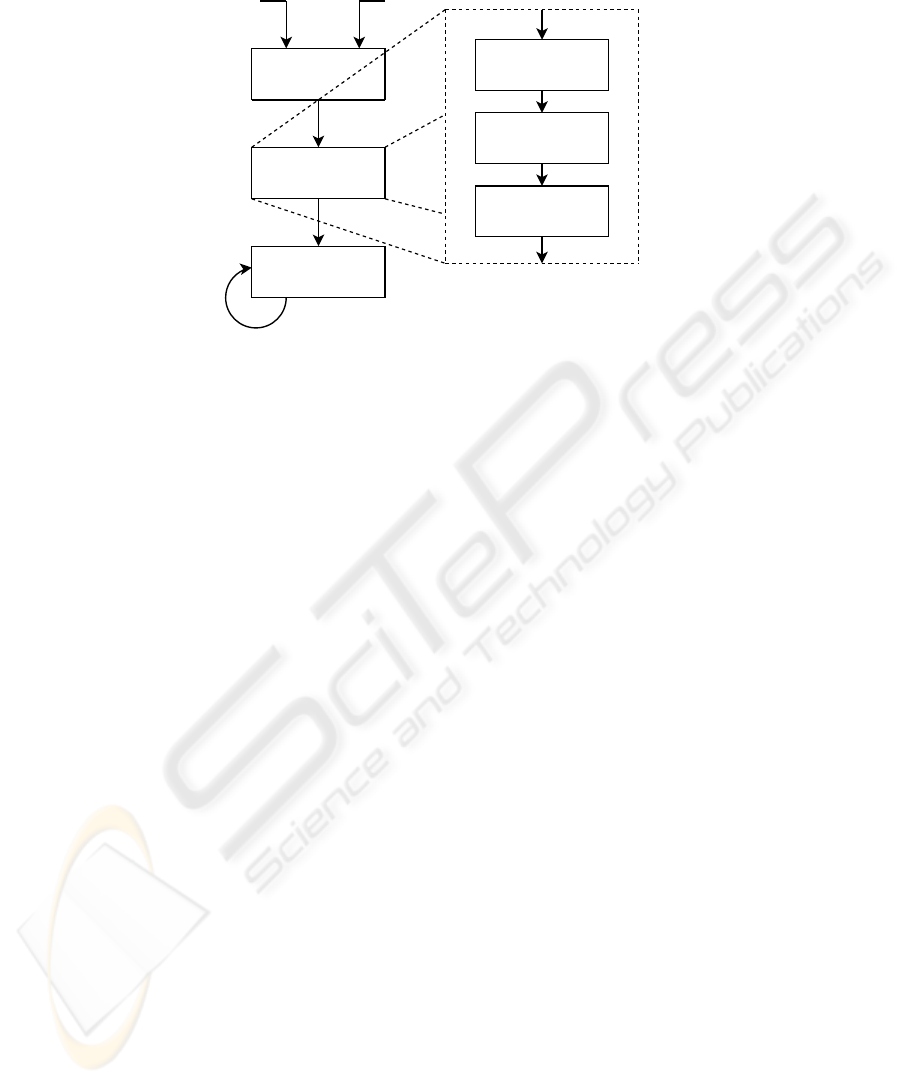
Data Association

(SUGR Framework)

Measure Estimation

(SUGR Framework)

Segment-based

Hierarchical EKF SLAM

Segments Points cloud

Segments

& Points cloud

Segment estrema

projection on the plane

Segment estimation

from projections

Plane estimation

from points cloud

Fig. 1. The sensor fusion mechanism.

By using the uncertain projective geometry framework we are able to extend the

original system by integrating the 3D segments coming from the feature-based trinocu-

lar stereo with the 3D points detected by the correlation-based stereo camera. Our idea

is to improve our original SLAM algorithm by integrating segments and points into 3D

segments; this is done by using the math introduced in Section 2, before introducing this

more reliable data in the EKF-based state ﬁlter. In this way we can reuse the original

ﬁlter, since we still base on segments to perform the SLAM. Moreover, being uncertain

projective geometry a probabilistic framework, we can also take into account uncertain-

ties in percepts, so to have a consistent estimate of the measurement uncertainties in the

ﬁlter.

3.1 Sensor Fusion Mechanism

Sensor fusion is performed before the measure of each segment is passed to the SLAM

algorithm; we say the fusion is performed “outside of the ﬁlter”. Following the ﬂowchart

in Figure 1, we perform hypothesis test to assign a sets of points to each segment by

using the Statistically Uncertain Geometric Reasoning (SUGR) framework. In this data

association phase, we identify three sets of points for each segment, using three hypoth-

esis tests: two tests, one for each extrema, are devoted to check if there are points to be

fused with the segment extrema, ehile the third test aims at searching points incident

to the support line in between the two extrema. It is important to notice that the SUGR

framework allows us to estimate, in a simple way, the 3D support line passing trough

the two extrema and its uncertainty as well. It is therefore possible to identify points

incident to the line by taking into account also the uncertainty in line estimation.

Having performed such tests, we are able to integrate each set of points with the

corresponding segment, updating both the position and the uncertainty of its extrema.

This activity is also performed “outside of the ﬁlter” and aims at generating a new

measure for the perceived 3D segments.

To have a more robust segment estimation, we decided to perform the integration by

following the three steps procedure outlined herefter. This is mainly due to the presence

of points that satisfy the test because of their large uncertainty: they usually belong to

the plane incident with the segment, but not necessary to the segment itself. For each

segment we:

1. Estimate a 3D plane incident to each point in the subset matching the incidence

hypothesis test.

2. Estimate the new extrema of the segment, estimating the two points incident to the

plane and equal to the old extrema, i.e., the point sets that passed the ﬁrst two tests.

3. Estimate the new segment by using these two projected extrema.

Now it is possible to pass the segments as new improved measures for the EKF in

the segment-based Hierachical SLAM algorithm described in [12, 11].

3.2 Using R*-Tree to Speed Up Slam Process

One of the problem of the SLAM process described in the previous sections is its com-

putational complexity. This is due to the huge size of 3D points clouds involved (i.e.,

a single acquisition with a correlation based sensor consists of ∼ 100K points). For

this purpose we decided to improve the algorithm by using an optimized data structure,

speeding up data association and segment-point fusion processes.

We propose the use of R*-Tree [13], a tree data structure that keeps data spatially

sorted and allows searches, insertions, and deletions in logarithmic amortized time.

Usually it is used in spatial access methods (i.e., for indexing spatial information like

the one in geographical information systems) and, in this case, we use it to index points

clouds acquired with che correlation based sensor, and the maps of segments as well.

The R*-Tree data structure splits space with hierarchically nested, and possibly

overlapping, minimum bounding rectangles (MBR); we have modiﬁed the original al-

gorithm to take into account the uncertainty of the data in the size of the MBR. Each

node of this tree has a variable number of entries (up to some pre-deﬁned maximum)

and each entry within a non-leaf node stores two pieces of data: the identiﬁer of a child

node, and the bounding box of all entries within this child node.

The insertion and deletion algorithms use the bounding boxes from the nodes to en-

sure that elements close in space are placed in the same leaf node (in particular, a new

element will go into the leaf node that requires the least enlargement in its bounding

box). Each entry within a leaf node stores again two pieces of information: the indenti-

ﬁer of actual data element (which, alternatively, may be placed directly in the node) and

the bounding box of the data element. Similarly, the searching algorithm, in this case a

K-Nearest Neighbor, uses the bounding boxes to decide whether or not to search inside

a child node. Most of the nodes in the tree are never “touched” during a search. The

R*-Tree attempts to reduce both coverage and overlap to improve further on the perfor-

mance, using a combination of a revised node split algorithm and the concept of forced

reinsertion at node overﬂow. This is based on the observation that tree structures are

highly susceptible to the order in which their entries are inserted, so an insertion-built

(rather than bulk-loaded) structure is likely to be sub-optimal. Deletion and reinsertion

of entries allows them to “ﬁnd” a place in the tree that may be more appropriate than

their original location.

(a) Comparison with ground truth for trinocular (b) 3D map from trinocular

based on simulated data

Fig. 2. Map estimated taking in input simulated data, in particular the input is just the segments

from the trinocular data.

(a) Comparison with ground truth for sensor fusion (b) 3D map from sensor fu-

sion based on simulated data

Fig. 3. Map estimated taking in input simulated data, in particular the input is the data fused

(segments+points) by using the uncertain geometry framework proposed.

4 Experimental Validation

In this section we show the capabilities of the framework presented in this paper, using

simulated and real data. Given a map of segments and the robot trajectory, we simulated

the image formation process on the two devices, as well as the uncertain measurements

of the world. The reason for using a simulated environment, to test the proposed method,

(a) 3D map from trinocular based on real data

(b) 3D map from sensor fusion based on real data

Fig. 4. Comparison between the same SLAM system, which takes in input different real data.

Top: the input is just the set of segments from the trinocular system. Bottom: the input is the

set of fused data (i.e., segments + points) obtained by using the framework proposed (only the

segments with at least ten associated points were used).

is to have access to the ground truth and perform, in this way, a numerical comparison

about the consistence of the EKF.

The two algorithm, i.e. the one with and the one without sensor fusion, have been

compared on the very same data. We expect that the differences between the two will

increase even more with real data.

In Figure 2 and Figure 3 it is possible to compare the results of the approach pro-

posed in this paper with our previous work on the trinocular based SLAM algorithm.

The plots refer to a circular trajectory of 40m and the SLAM algorithm has been stopped

before loop closure to underline the relevance of the approach. In Figures 2(a) and 3(a),

we plotted the ±3σ conﬁdence ellipse around the estimated robot pose. It can be noticed

how the estimate of robot pose with the trinocular based system eventually becomes in-

consistent; on the other hand, using sensor fusion helps in maintaining it consistent.

Figures 2(b) and 3(b) allow mapping comparison. Notice that by using trinocular

data and SVS points we are able to reduce the uncertainty in the segment extrema

(ellipses in the plots) and to improve the overall accuracy.

In Figure 4 it is possible to compare the results based on real data acquired in a

corridor. The measured segments and points, in this case, are more noisy than simulated

ones and it is common to obtain, before the fusion step, “spurious” segments. To reduce

this undesired effect, we decided to ﬁlter the segments using a simple criterion: use only

1010

the segments with at least ten points associated. This allows to estimate a map with

less ”spurious” segments than that obtained using only trinocular segments. Figure 4

demonstrates the quality that can be reached with the proposed approach, which allows

to combine non-homogeneous features of the scene, i.e., 3D segments and 3D points,

into a single representation, segment-based in our case

5 Conclusions and Future Works

This paper presents a 6DoF SLAM algorithm that exploits the uncertain projective ge-

ometry framework to perform sensor fusion of 3D data coming from different sensors.

The framework allows to represent 3D segments and 3D points with their associate

uncertainty. Although the algorithm presented in this paper deal with vision data, it is

straightforward to include other source of 3D information in the framework. For in-

stance, laser scans could be integrated either using single measures as points, extracting

3D lines, or computing 3D planes, when dealing with 3D laser scans.

We faced sensor fusion by exploiting uncertain projective geometry, outside the

SLAM EKF state ﬁlter, to provide a new “virtual” sensor with the purpose of reduc-

ing measurement errors and improving the results obtained with the SLAM algorithm.

The described framework could be used within the SLAM algorithm as well, for data

association, trough hypothesis test, and ﬁlter update.

Moreover we demonstrated that it is possible to use this algorithm also with real

data, using points not only to improve the estimated map, but also to remove erroneous

measurements from data.

In the last years many researchers have demonstrated that it is possible to use picto-

rial features from a monocular camera to perform SLAM as well. Notable examples are

the works of Lacroix et al.[14], Davison et al.[15] and Lowe et al.[16]. The key idea, in

this kind of approaches, is to use interest points as features, trying to fulﬁll the data as-

sociation task by the use of image descriptors or correlation based methods. Usually, to

have signiﬁcant landmarks, these descriptors are chosen to be invariant to image scale,

rotation, and partially invariant (i.e. robust) to changing viewpoints, or illumination.

From a SLAM point of view this is very useful not only for the data association but also

because it allows the robot to identify possible loop closures.

We are presently working on the integration of these pictorial feature in the frame-

work proposed by this paper. Manipulating uncertain geometric entities, we are able

to treat interest points as delimited portions of uncertain planes, enriched by an ap-

pearance information represented by the image patch located around the point on the

image plane. Performing the data association among frames, we could estimate the

most probable plane where the feature lies and, at the same time, update the appearance

information depending on its position relative to the camera orientation.

Acknowledgements

This work has partially been supported by the European Commission, Sixth Frame-

work Programme, Information Society Technologies: Contract Number FP6-045144

(RAWSEEDS), and by Italian Istitute of Tecnologogy (IIT) grant.

1111

References

1. Durrant-Whyte, H.F.: Integration, coordination and control of multi-sensor robot systems.

Kluwer Academic (1987)

2. Lu, F., Milios, E.: Globally consistent range scan alignment for environment mapping. Au-

tonomous Robots 4 (1997) 333–349

3. Tard

os, J.D., Castellanos, J.A.: Mobile robot localization and map building: a multisensor

fusion approach. Kluwer Academic (1999)

4. Marzorati, D., Matteucci, M., D. Migliore, D.G.S.: Integration of 3d lines and points in 6dof

visual slam by uncertain projective geometry. European Conference on Mobile Robotics

(2007) 96 – 101

5. N

uchter, A., Lingemann, K., Hertzberg, J.: 6D SLAM with Cached kd-tree Search. Number

06421 in Dagstuhl Seminar Proceedings. Internationales Begegnungs- und Forschungszen-

trum f

ur Informatik (IBFI), Schloss Dagstuhl, Germany, Dagstuhl, Germany (2007)

6. N

uchter, A., Lingemann, K., Hertzberg, J., Surmann, H.: 6d slam with approximate data

association. 12th International Conference on Advanced Robotics, 2005. ICAR ’05. Pro-

ceedings (2005) 242–249

7. Heuel, S.: Points, Lines and Planes and their Optimal Estimation. Number 2191 in LNCS.

Springer (2001)

8. Heuel, S.: Uncertain Projective Geometry: Statistical Reasoning for Polyhedral Object Re-

construction. Springer (2004)

9. Konolige, K.: Small vision system. hardware and implementation. In: ISRR, Hayama, Japan

(1997)

10. Ayache, N., Lustman, F.: Trinocular stereo vision for robotics. IEEE Trans. on PAMI 12

(1991)

11. Marzorati, D., Sorrenti, D.G., Matteucci, M.: Multi-criteria data association in 3d-6dof hier-

archical slam with 3d segments. In: Proc. of ASER06 Conf. (2006)

12. Marzorati, D., Sorrenti, D.G., Matteucci, M.: 3d-6dof hierarchical slam with trinocular vi-

sion. In: Proc. of ECMR. (2005)

13. Beckmann, N., Kriegel, H.P., Schneider, R., Seeger, B.: The r*-tree: An efﬁcient and robust

access method for points and rectangles. SIGMOD Conference (1990) 322–331

14. Lemaire, T., Lacroix, S., Sola, J.: A practical 3d bearing-only slam algorithm. In: Proc. of

IROS. (2005)

15. Davison, A.: Real-Time Simultaneous Localisation and Mapping with a Single Camera. In:

Proc. of ICCV. (2003) 1403–1410

16. Se, S., Lowe, D., Little, J.: Global localization using distinctive visual features. In: Proc. of

IROS, Lausanne, Switzerland (2002)

1212