Mutual Calibration of a Camera and a Laser

Rangeﬁnder

Vincenzo Caglioti, Alessandro Giusti and Davide Migliore

Politecnico di Milano, Dipartimento di Elettronica e Informazione, Italy

Abstract. We present a novel geometrical method for mutually calibrating a

camera and a laser rangeﬁnder by exploiting the image of the laser dot in relation

to the rangeﬁnder reading.

Our method simultaneously estimates all intrinsic parameters of a pinhole natural

camera, its position and orientation w.r.t. the rangeﬁnder axis, and four parame-

ters of a very generic rangeﬁnder model with one rotational degree of freedom.

The calibration technique uses data from at least 5 different rangeﬁnder rota-

tions: for each rotation, at least 3 different observations of the laser dot and the

respective rangeﬁnder reading are needed. Data collection is simply performed

by generically moving the rangeﬁnder-camera system, and does not require any

calibration target, nor any knowledge of environment or motion.

We investigate the theoretical limits of the technique as well as its practical ap-

plication; we also show extensions to using more data than strictly necessary or

exploit a priori knowledge of some parameters.

1 Introduction

We consider a rangeﬁnder-camera system and a solidal frame of reference F ; the range-

ﬁnder itself can rotate around a generic axis solidal to F . After the mutual calibration

is completed, we can:

– recover the viewing ray (in the reference frame F ) associated to any image point

(camera calibration);

– recover the measuring ray (in the reference frame F ) associated to any rangeﬁnder

angle, and a point on this ray which returns a zero reading (rangeﬁnder calibration).

Mutual rangeﬁnder-camera calibration is needed for relating rangeﬁnder readings to

the respective image points; this is a prerequisite for correlating rangeﬁnder and image

data, which is useful for many practical tasks such as obstacle detection and characteri-

zation, 3D shape and texture reconstruction, robot self-localization, odometry and map-

ping. Our proposed solution does not require any speciﬁc calibration object, and can be

performed automatically by just sampling rangeﬁnder readings and camera images dur-

ing generic relative motion of the rangeﬁnder-camera system or the surrounding scene:

the only requirement is that you get at least three different range readings for each of

ﬁve different rangeﬁnder angles.

Caglioti V., Giusti A. and Migliore D. (2008).

Mutual Calibration of a Camera and a Laser Rangeﬁnder.

In VISAPP-Robotic Perception, pages 33-42

DOI: 10.5220/0002341700330042

 SciTePress

The problem is hard since it is characterized by many variables and degrees of free-

dom, related to the camera characteristics, camera position, and rangeﬁnder construc-

tion. In its most general form, the problem assumes almost no knowledge on the system

characteristics and environment parameters; on the other hand, each of our observations

is very basic and it only consists in a point on the image and the related rangeﬁnder

reading. When compared to the problem of calibrating a camera alone without any

prior knowledge of the environment (autocalibration), our technique is surprising for its

simplicity, expecially if accounting for the additional degrees of freedom which char-

acterize this scenario. This is intuitively explained by considering that our technique

exploits some properties of the rangeﬁnder function (such as the linearity of the mea-

suring ray): therefore, while being calibrated, it also provides constraints for camera

calibration, and vice-versa. An intersting related work from this point of view is [8],

which calibrates a camera using a laser pointer as a calibration device.

Our work heavily relies on known techiques in projective geometry [5]. In particu-

lar, our camera calibration technique is related to the method introduced by Colombo

et al. in [2], which calibrates a camera using coaxial circles; other interesting alge-

braical properties of coplanar circles for camera calibration and 3D structure extraction

are presented in [4, 6]. The problem of simultaneously calibrating a camera and a laser

rangeﬁnder has been recently challanged with several approaches: in [9], a checker-

board calibration pattern is used, and its images and distance proﬁles are related in

order to ﬁnd the camera position and orientation w.r.t. the rangeﬁnder; in [1] a special

3D calibration object allows to automatically calibrate a laser rangeﬁnder. Our tech-

nique is different in that it does not use any explicit calibration target, but exploits the

visible image of the laser dot; a similar approach is found in [7], where some alge-

braic constraints on the camera-rangeﬁnder calibration due to the laser dot visibility are

derived.

In Section 2 we formally deﬁne the problem and its parameters and variables. Sec-

tion 3 presents our technique, and sketches the extension to 2-DOF rangeﬁnders. Sec-

tion 4 discusses the results, and proposes variations for calibrating only a subset of the

parameters, and using more data than strictly needed.

2 Deﬁnitions, Model and Data

2.1 System Model

We consider a camera-rangeﬁnder system; the rangeﬁnder has 1 rotational DOF around

a generic axis; the rangeﬁnder rotation angle φ is not calibrated – i.e., the actual angle

is not necessarily known, but repeatable.

We deﬁne a reference frame F as follows:

– F

coincides with the rangeﬁnder rotation axis;

– F

is parallel to the projection on the xy plane of the rangeﬁnder ray when φ = 0;

– the origin is placed at the nearest point on the rotation axis to any telemeter ray.

3434

Fig. 1. Left: geometrical model of the system. Right: the minimal number of observations. For

each of the observed laser dots, the corresponding rangeﬁnder measure is known. At least three

points are needed for each of 5 rangeﬁnder angles.

2.2 System Parameters

Let r be a generic rangeﬁnder ray; the rangeﬁnder parameters are the following:

– the distance d

between r and F

;

– the angle η between r and F

;

– the distance d

between the point on r originating a zero rangeﬁnder reading and

the point on r nearest to F

The camera parameters are expressed by the familiar perspective camera calibration

matrix P . More speciﬁcally, the intrinsic parameters are summarized by the K matrix,

on which we assume null skew factor, resulting in 4 degrees of freedom: aspect ratio a,

focal length f , and the principal point coordinates u

, v

. By considering 6 additional

degrees of freedom for the camera generic position and rotation w.r.t. F , the camera

model is characterized by 10 degrees of freedom.

In total, we are going to estimate a total of 13 system parameters.

2.3 Observation Model

The calibration procedure is based on a set of observations. Each observation o is char-

acterized by:

– a rangeﬁnder rotation angle φ, not necessarily calibrated but repeatable;

– a rangeﬁnder reading m;

– an image point p = (u, v), where the laser dot is observed.

We assume that the rangeﬁnder reading is linear w.r.t. the actual distance in the scene,

up to the constant additive factor modeled by the rangeﬁnder parameter d

φ and m identify a point in space, therefore they uniquely deﬁne the image point p

through the camera calibration matrix P and the rangeﬁnder parameters.

3535

3 Calibration Procedure

3.1 Data Gathering

Our calibration procedure uses at least 15 observations; in Section 4 we show how the

procedure is extended in order to take advantage of additional observations or parame-

ters known a priori.

We consider 5 different φ angles φ

i = 1..5. For each i, we need 3 observations

i,j

j = 1..3 characterized by different m values. These observations can be easily

automatically gathered by simply moving the camera-rangeﬁnder system in an environ-

ment, or by moving large objects in front of the still system.

i,j

= {i, m

i,j

, p

i,j

} (1)

3.2 Recovering Images of Coaxial Circles

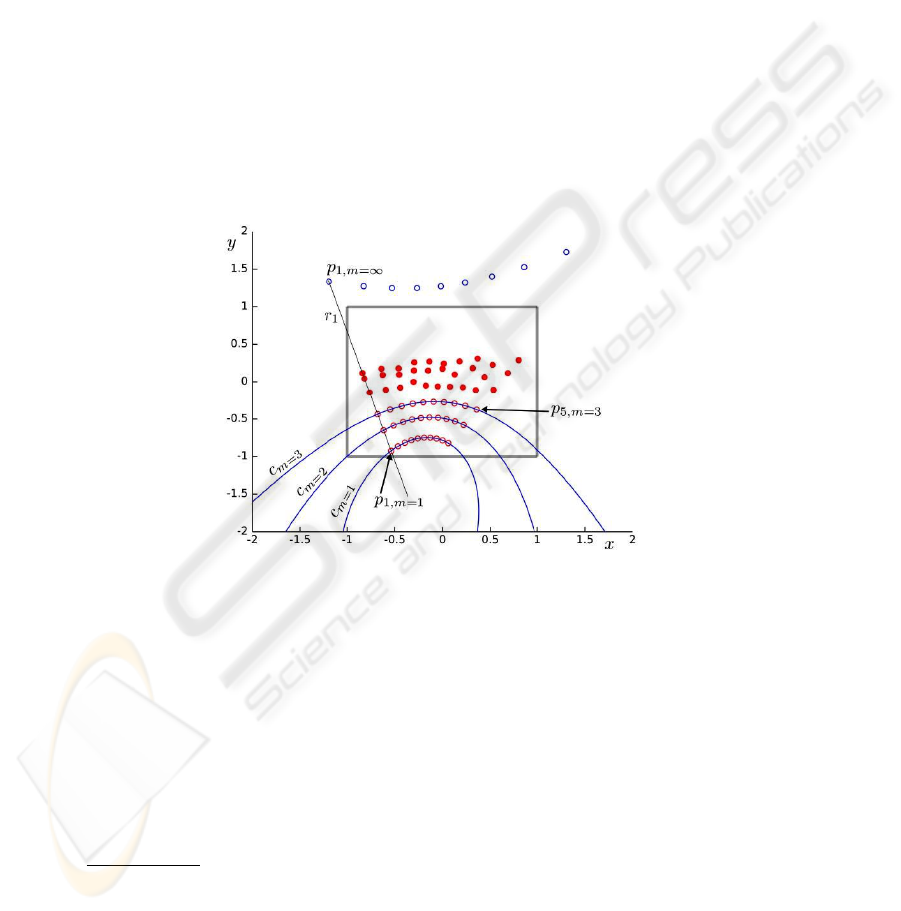
Fig. 2. Three conics can be recovered by exploiting the cross ratio invariance under perspective

transformations. Note that in this ﬁgure, observations for more than 5 angles are depicted.

i,1

, p

i,2

, p

i,3

are image points all lying on the same image line r

because they

are projections of scene points P

i,1

, P

i,2

, P

i,3

(the laser dots) lying on the same scene

line, i.e. the rangeﬁnder ray R

. The distances between scene points P

i,1..3

are known

from the respective rangeﬁnder readings m

i,1..3

: therefore, by exploiting the cross ra-

tio invariance under a perspective transformation, any point on image line r

can be

associated to the related rangeﬁnder reading.

Let p

i,m=x

be the image point projection of the laser dot associated to rangeﬁnder

reading x. We can now retrieve p

i,m=x

for any x. Then we compute p

i,m=1

, p

i,m=2

and

i,m=3

Even if the camera-rangeﬁnder system is moved for gathering the observations, we are cur-

rently considering reference frame F , which is solidal with the system itself

3636

The procedure can be repeated for all of the 5 angles φ

i = 1..5. As a result, we get

another set of 15 points, corresponding to the projections of the laser dots associated to

the rangeﬁnder readings m = 1, m = 2 and m = 3 for each of the 5 φ

angles. Note

that some of these image points may lie outside the imaged part of the image plane.

The 5 image points p

i,m=x

(with i = 1..5) all lie on a conic c

m=x

, because they

are projections of scene points lying on a circumference C

m=x

in the scene. The axis

of C

m=x

is the rangeﬁnder rotation axis F

. We can reconstruct c

m=1

, c

m=2

and c

m=3

as we have 5 points belonging to each.

3.3 Computing the Camera Intrinsic Parameters

The images c

m=1

, c

m=2

and c

m=3

of three coaxial circles allow to calibrate the camera

parameters, and to recover the camera position with respect to the rangeﬁnder. The

ﬁrst step is to exploit c

m=1

, c

m=2

and c

m=3

in order to identify some vanishing points

representing orthogonal directions; then, the intrinsic camera parameters are determined

by exploiting the image of the absolute conic. We now describe the procedure in grater

detail.

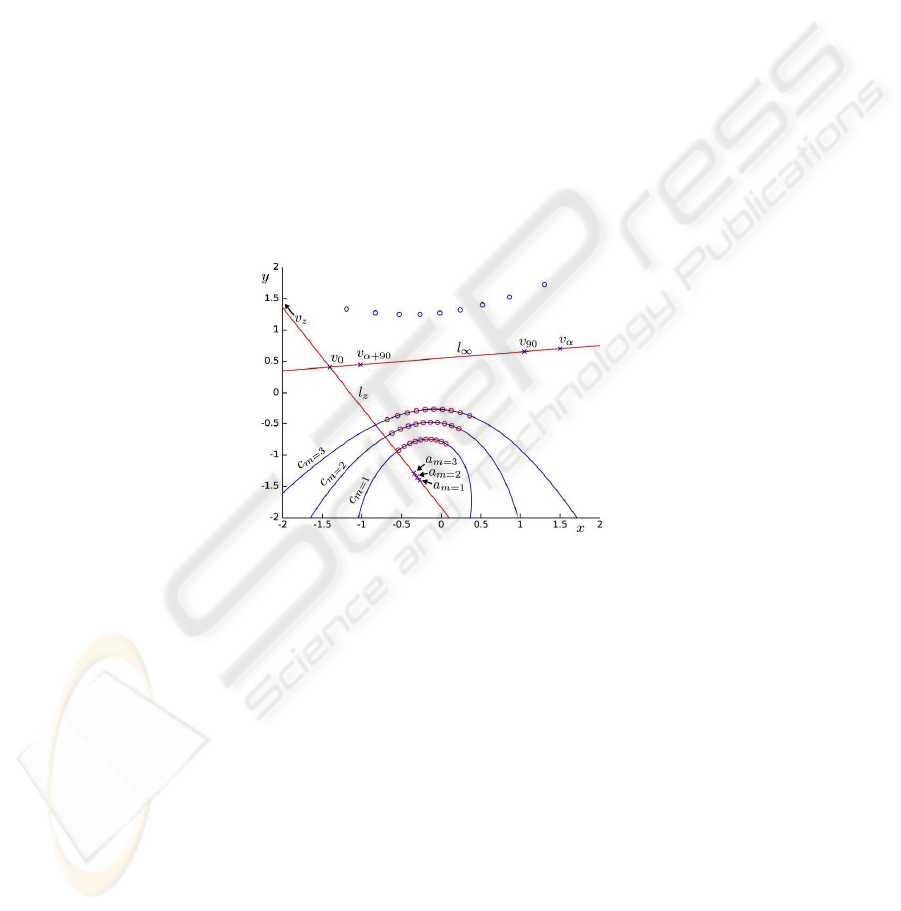
Fig. 3. The three conics allow us to derive a number of vanishing points, from which the camera

intrinsic parameters can be computed.

At ﬁrst, we compute the intersection points of the three conics. The only two com-

mon intersection points are the projections of the two circular points of the xy plane;

they deﬁne the line at the inﬁnity l

∞

of the xy plane in the image (horizon).

Let A

m=x

be the center of C

m=x

, and a

m=x

its projection. a

m=1

m=2

, a

m=3

) is

easily found as the pole of l

∞

with respect to c

m=1

m=2

, c

m=3

Let l

be the projection of the F

axis in the image. Since A

m=1

, A

m=2

and A

m=3

are aligned and lying on F

, l

is determined as the line passing through the a

m=x

points.

We name v

the intersection of l

with l

∞

, representing the horizontal vanishing

point associated to a direction belonging to the symmetry plane which is deﬁned by

the camera center and rangeﬁnder rotation axis. A vanishing point v

perpendicular to

such symmetry plane is found as the pole of l

with respect to any of the c

m=x

conics.

3737

Let v

be a different vanishing point randomly chosen on l

∞

; the vanishing point

α+90

is found as the intersection of l

∞

with the polar line of v

with respect to any of

the c

m=x

conics. v

α+90

represents a direction parallel to the xy plane and perpendicular

to the direction associated to v

Let v

be the vanishing point representing the F

direction. v

lies on l

; its exact

position can be recovered by considering points a

m=1

, a

m=2

and a

m=3

, which are

projections of equidistant points on F

; by means of the cross-ratio invariance, v

easily determined.

In order to ﬁnd the camera intrinsic parameters, we exploit the image ω of the

absolute conic [5, 2]. ω can be recovered by exploiting orthogonality relations between

couples of the ﬁve vanishing points v

, v

0, v

, v

90+α

and v

, which translate to four

linear equations: v

ωv

α+90

= 0; v

ωv

= 0; v

ωv

= 0; and v

ωv

= 0

Once ω is known, the matrix K containing the camera intrinsic parameters can be

found using the Cholesky decomposition since ω = K

−T

−1

3.4 Recovering the Rangeﬁnder Parameters

Computing η. The η angle between rangeﬁnder rays and the rotation axis F

is eas-

ily recovered as the angle between the direction associated to a point p

i,m=∞

(which

represents a vanishing point of a rangeﬁnder ray direction) and the direction associated

to v

; the angle between said directions can be computed since the camera intrinsic

parameters are now known.

i,m=∞

also allows us to recover the actual value of φ

, which was not previously

known: in fact, the projection of R

’s direction on the xy plane is identiﬁed by a van-

ishing point at the intersection between l

∞

and the join of p

i,m=∞

and v

; we can then

measure φ

in relation to the direction identiﬁed by v

The Radius of Circles C

m=x

. In order to recover the remaining rangeﬁnder parame-

ters, we need to recover the radius of circles C

m=x

Fig. 4. The shape of the locus of rangeﬁnder rays (a ruled quadric). The three circumferences

m=1

, C

m=2

and C

m=3

are shown. Note that their radius varies along the F

axis as an hyper-

bola.

We consider the two circles C

m=1

and C

m=2

, and the points P

1,m=1

, P

1,m=2

lying

on them, belonging to rangeﬁnder ray R

. Let λ be the radius of C

m=1

: we are going to

3838

recover λ by writing an equation involving the length of the projection on the xy plane

of segment P

1,m=1

1,m=2

Let γ

m=1

be the (horizontal) direction of the radius A

m=1

1,m=1

. γ

m=1

is easily

recovered as the direction associated to the vanishing point found at the intersection

between l

∞

and the line on which said radius lies; the same holds for direction γ

m=2

of the radius A

m=2

1,m=2

Let κ be the ratio between radii κλ = A

m=2

1,m=2

and λ = A

m=1

1,m=1

. κ

can be recovered as follows: consider the image line bitangent to c

m=1

and c

m=2

at the

same side w.r.t. l

; let a

be the intersection point between said bitangent and l

, and A

its backprojection on F

. κ is now found as the ratio between the lengths of segments

m=2

and A

m=1

, which is computed exploiting the cross ratio invariance as:

κ = 2 ·

m=2

· a

m=0

m=1

· a

m=0

m=2

. (2)

We ﬁnally get a single equation in the single unknown λ, which leads to:

λ = cos(η)/



κ cos(γ

m=1

) − cos(γ

m=2

)

κ sin(γ

m=1

) − sin(γ

m=2

)



. (3)

Once λ is known, the radii of C

m=2

and C

m=3

are easily found.

Computing d

and d

. We can now consider the function y = f(x) relating a

rangeﬁnder measure x to the radius of C

m=x

: it is a hyperbola with vertical axis, and

asymptotes forming an angle η with the x axis. Since we also have three points, we can

identify the hyperbola. Its vertex’ x and y coordinates are the rangeﬁnder parameters

−d

and d

, respectively. Alternatively, d

can be recovered as the distance between the

3D line overlapping F

and the measuring ray which is easily identiﬁed by using the

data computed so far. d

immediately follows.

This concludes the calibration of the rangeﬁnder parameters.

3.5 Recovering the Camera Position and Rotation

Recovering the camera position and rotation in the reference frame F is now possible.

The camera rotation matrix is easily computed from the location of vanishing points v

and v

. In order to compute the camera position, we can exploit the image of one of the

diameters of C

m=1

, whose 3D coordinates are now known.

4 Extensions, Discussion and Practical Issues

4.1 Degenerate Cases

If the camera center lies on the F

axis, the centers of all circumferences C

m=x

project

to the same image point; therefore, the presented technique does not apply.

Another degenerate case happens if η = 0 deg: then, the described procedure does

not allow the camera intrinsic parameters to be calibrated. Still, the ﬁrst steps of our

3939

technique still allow us to recover a set of concentric, coplanar circles: by gathering

a ﬁrst complete set of observations followed by another set acquired with a different

camera pose, the camera parameters can be calibrated and the rest of the procedure

follows with trivial modiﬁcations.

4.2 Exploiting Additional Observations

Since data gathering is such an easy and practical task, many additional observations

may be available in most scenarios with little additional effort. Our technique is easily

adapted to exploiting them, in order to improve the results accuracy and robustness to

noise.

For each of the φ

angles, we require at least three observations in order to recover

i,m=x

points by exploiting cross ratio invariance. If more than three different obser-

vations for a given φ

angle are available, the cross ratio can be estimated robustly to

noise. Note that measurement errors originate both from noise on the rangeﬁnder read-

ings, and from uncertainty in the laser dot localization in the image.

If at least three observations are provided for more than ﬁve different φ angles, each

of the additional angles provides one extra point for estimating c

m=x

conics, which im-

proves noise resilience as well; then, known conic ﬁtting techniques [3] can be applied.

Each of the p

i,m=x

points may be weighted differently, based on its conﬁdence.

4.3 Exploiting a Priori Knowledge

In many scenarios, some of the system parameters may be known a priori; then, our

technique can be adapted in order to exploit this knowledge, in order to improve noise

resilience. Some common scenarios follow:

= 0 : in this case, the surface deﬁned by the rangeﬁnder rays is a cone: the last

part of the calibration can therefore be skipped; in fact, once λ is computed, d

immediately found.

Rangeﬁnder parameters known: if all the rangeﬁnder parameters are known a priori

and the φ angle of each observation is calibrated, rangeﬁnder rays and laser dot

coordinates can be localized in reference frame F . Camera calibration then reduces

to the well-studied scenario in which all of the observed points have a known 3D

position.

Camera intrinsic parameters known : in this case, the ﬁrst steps of the technique can

be skipped.

4.4 Visibility and Localization of the Laser Dot

Localizing the laser dot in an image is a task which is easily made automatic even in

lit environment: a simple solution, also suggested in [7] is shooting two images, one

with the laser on and one with the laser off; the difference image between the two then

isolates the laser dot, whose exact coordinates can be taken either by ﬁrst binarizing the

image then using the skeletonize morphological operator, or by computing the barycen-

ter of the spot.

4040

In order to localize the dot, an obvious prerequisite is that it is actually visible in the

image: this may be a problem when using a laser working in the near-infrared wave-

lengths, whose dots will therefore irradiate light outside the visible part of the elec-

tromagnetic spectrum: although image sensors are very sensible to such wavelengths,

sometimes cameras use ﬁlters to minimize their effect, which should be removed.

5 Experimental Results and Implementation Notes

First, the technique has been validated by implementing a matlab-based simulator of the

camera-rangeﬁnder system, also accounting for a customizable amount of normally-

distributed noise affecting both the image coordinates of the laser dot projection and

the readings of the rangeﬁnder; we also developed a matlab implementation of the cali-

bration technique. When operating on clean data, the procedure yields results perfectly

adhering to ground truth (up to negligible errors due to numerical precision issues); this

validates the soundness of our approach. Figures 1 (right), 2 and 3 are related to such

experiments, with the following parameters: d

= 2, d

= 1, η = π/8, and a natural

camera with the principal point at the center of the image plane and focal length 0.55

times the image width. When adding noise, the quality of results drops rather dramat-

ically, due to the geometrical nature of the technique which is not resilient to noise.

In particular, intersecting conics returns unreliable circular points. Implementing the

techniques introduced in Section 4.2 allows to exploit additional observations, thus im-

proving noise resilience.

Fig. 5. Left: addition of many images shot in a dark room: the laser dots and their alignment are

visible; the dataset associates a range measurement with each. Right: part of the construction in

another real setting, on the background of one of the 92 images comprising the dataset; observa-

tions (red dots) and ﬁtted lines (black); computed image points corresponding to 200mm, 400mm

and 600mm measures (red circles); ﬁtted conics (blue ellipses); l

∞

is over the top of the image.

Note signiﬁcant span of φ angles, which enables a much improved conic ﬁtting.

We also applied the technique to camera images, acquired in two different sets with

different parameters, composed by 77 and 92 observations, respectively. Due to noise

in the image and rangeﬁnder readings, all the observations must be exploited in order to

complete the calibration procedure correctly. However, we identiﬁed that some steps of

4141

the technique, such as the intersection of conics for ﬁnding l

∞

, are acting as bottlenecks

and being severely affected by noise. Such steps of the algorithm are currently being

improved and substituted with noise-resilient implementations in order to improve cal-

ibration accuracy in presence of noise.

6 Conclusions and Future Works

We developed a geometrical technique for mutually calibrating a camera and a laser

rangeﬁnder. The technique is attractive because of its generality, and because it does

not assume anything about the environment; the data collection step is also extremely

simple and straightforward.

We validated the technique by using both real and simulated data: the results conﬁrm

the correctness of the approach, but also highlight the expected weakness to noise in

the data when using the minimal amount of observations. In order to be practical in

real scenarios, we described a number of possible improvements aimed at increasing

robustness to noise; in particular, since data collection is fast and simple, the process

can be automated and may gather a large amount of observations.

We are currently implementing modiﬁcations to the technique in order to maxi-

mally exploit all available data, and replacing steps heavily affected by noise with noise-

resilient alternatives. Moreover, we are planning an extension for the mutual calibration

of a camera and a SICK laser rangeﬁnder, whose scans are visible in the images as

jagged lines.

References

1. M. Antone and Y. Friedman. Fully automated laser range calibration. In Proc. of BMVC 2007.

2. Carlo Colombo, Dario Comanducci, and Alberto Del Bimbo. Camera calibration with two

arbitrary coaxial circles. In Proc. of ECCV 2006.

3. Andrew W. Fitzgibbon and Robert B. Fisher. A buyer’s guide to conic ﬁtting. In Proceedings

of BMVC 1995.

4. Pierre Gurdjos, Peter Sturm, and Yihong Wu. Euclidean structure from n >= 2 parallel

circles: Theory and algorithms. In Proc. of ECCV 2006.

5. R. I. Hartley and A. Zisserman. Multiple View Geometry in Computer Vision. 2004.

6. G. Jiang, H. Tsui, L. Quan, and A. Zisserman. Geometry of single axis motions using conic

ﬁtting. 2003.

7. C. Mei and P. Rives. Calibration between a central catadioptric camera and a laser range ﬁnder

for robotic applications. In Proc. of ICRA 2006.

8. Tom

s Svoboda, Daniel Martinec, and Tom

s Pajdla. A convenient multi-camera self-

calibration for virtual environments. PRESENCE: Teleoperators and Virtual Environments.

9. Qilong Zhang and R. Pless. Extrinsic calibration of a camera and laser range ﬁnder (improves

camera calibration). In Proc. of IROS 2004.

4242