AUTOMATIC RECOGNITION OF LEAVES BY SHAPE

DETECTION PRE-PROCESSING WITH ICA

Jordi Solé-Casals

Signal Processign Group, University of Vic, Sagrada Família 7, E-08500, Vic, Spain

Carlos M. Travieso, Miguel A. Ferrer, Jesús B. Alonso

Department of Signals and Communications, Technological Centre for Innovation on Communication (CeTIC)

University of Las Palmas de Gran Canaria, Campus de Universitario

Tafira s/n, E-35017, Las Palmas de Gran Canaria, Spain

Juan Carlos Briceño

Computer Science Department. University of Costa Rica

Sede "Rodrigo Facio Brenes", Montes de Oca, Post-Code 2060, San José, Costa Rica

Keywords: Independent Component Analysis, Pattern Recognition, Leaves Recognition, Parameterization, Artificial

Neural Networks.

Abstract: In this work we present a simulation of a recognition process with perimeter characterization of a simple

plant leaves as a unique discriminating parameter. Data coding allowing for independence of leaves size and

orientation may penalize performance recognition for some varieties. Border description sequences are then

used to characterize the leaves. Independent Component Analysis (ICA) is then applied in order to study

which is the best number of components to be considered for the classification task, implemented by means

of an Artificial Neural Network (ANN). Obtained results with ICA as a pre-processing tool are satisfactory,

and compared with some references our system improves the recognition success up to 80.8% depending on

the number of considered independent components.

1 INTRODUCTION

Recognition of tree varieties using samples of

leaves, in spite of its biological accuracy limitations,

is a simple and effective method of taxonomy (Lu et

al., 1994). Laurisilva Canariensis is a relatively

isolated tree species, in the Canary Islands,

biologically well studied and characterized. Twenty-

two varieties are present in the archipelago and have

simple and composed regular leaves. Our study

takes into account sixteen of the twenty-two simple

leaf varieties, with totals of seventy-five individuals

per each one. They have been picked over different

islands, pressed (for conservation purposes) and

scanned in gray tonalities.

From a biological perspective, attention has to be

brought to the fact that emphasis on structural

characteristics, which are consistent among

individuals of a species, instead of quality

parameterization (as colour, size or tonality),

improves recognition performance.

Quality parameterization lack of accuracy is due

to the fact of leaves individual variability on the

same variety as well on leaf variability on a single

plant. Plant age, light, humidity, context behaviour

or distribution of soil characteristics, among other

things, contributes for such anomaly.

In spite of the fact that we may consider several

biological parameters, as we have done previously

(Loncaric, 1998), in order to generalize such study,

in this paper we have just considered a border

parameterization. This system was classified by

Hidden Markov Model (HMM) (Rabiner et al.,

1998) achieving a success of 78.33% (Briceño et al.,

2002), and by SVM (Burges, 1998) with Principal

Component Analysis (PCA) (Jolliffe, 2002) as pre-

processing, achieving a success of 90.54%. (Solé-

Casals et al., 2008)

462

Solé-Casals J., Travieso C., Ferrer M., Alonso J. and Briceño J. (2009).

AUTOMATIC RECOGNITION OF LEAVES BY SHAPE DETECTION PRE-PROCESSING WITH ICA.

In Proceedings of the International Conference on Bio-inspired Systems and Signal Processing, pages 462-467

DOI: 10.5220/0001430404620467

 SciTePress

In this present work, we have improved previous

studies using the transformation and reduction of

border parameterization using Independent

Component Analysis (ICA) (Jutten et al., 1991)

(Hyvärinen et al., 2001) and classifying its result

with a Multilayer Perceptron Neural Network (MLP)

(Duda et al., 2000) (Bishop, 1996).

Figure 1: Images of the 16 varieties of canariensis

laurisilva considered for the present study. Images are

presented regardless of size.

2 LEAVES DATABASE

In order to create a recognition system of different

vegetable species it is necessary to build a database.

This database should contain the samples of the

different species of study. The number of samples

will be large enough to, first train the classifier with

guarantees and second, test this classifier to assess

the results obtained. On top of this, the amount of

chosen samples, for each vegetable species must

cover the largest amount of shapes and structures

that this unique specie can take. In this way, a robust

study of the different vegetable species is ensured.

Attending to this reasoning, the sample

collection was made at different times of the year,

trying in this way to cover all the colours and shapes

that the leaves take throughout the four seasons.

Besides, a special attention was made to reject those

samples that were degraded so that the selected

samples were in good condition.

Therefore, this database is composed of 16

classes (see Figure 1), with 75 samples each one.

The images that form the database has been stored in

a grey scale using a "jpeg" format (Joint

Photographic Experts Group) with Huffman

compression. The images have been digitalized to

300 dpi, with 8 bit accuracy.

3 PARAMETERIZATION

SYSTEM

We have considered just the leaf perimeter. This

image is considered without its petiole that has been

extracted automatically from the shadow image.

Leaves are scanned fixed on white paper sheets,

placed more or less on the center, upward (petiole

down) and reverse side to scan.

Border determination as (x,y) positioning

perimeter pixels of black intensity, has been

achieved by processes of shadowing (black shape

over white background), filtering of isolated points,

and perimeter point to point continuous follow.

3.1 Perimeter Interpolation

As shown in table 1, perimeter size variability

induces us to consider a convenient perimeter point

interpolation, in order to standardize perimeter

vector description. For an interpolating process, in

order to achieve reconstruction of the original shape,

we may use any of the well known algorithms as

mentioned in (Lu et al., 1994), (Loncaric, 1998),

(Huang et al., 1996), but a simple control point’s

choice criterion in 1-D analysis allows for an

appropriate performance ratio on uniform control

point’s number and approximation error for all

individuals of all varieties studied.

The general idea, for such choice, is to consider

(x,y) positional perimeter points as (x,F(x)) graph

points of a 1-D relation F.

Consideration of y coordinate as y = F(x) is

done, because of the way, leaves images are

presented in our study: leaves have been scanned

with maximum size placed over x ordinate.

For a relation G to be considered as a one-

dimensional function, there is need to preserver a

correct sequencing definition (monotonic

behaviour). That is: A graph

)}(/),(,..1{

xniG =

(1)

AUTOMATIC RECOGNITION OF LEAVES BY SHAPE DETECTION PRE-PROCESSING WITH ICA

463

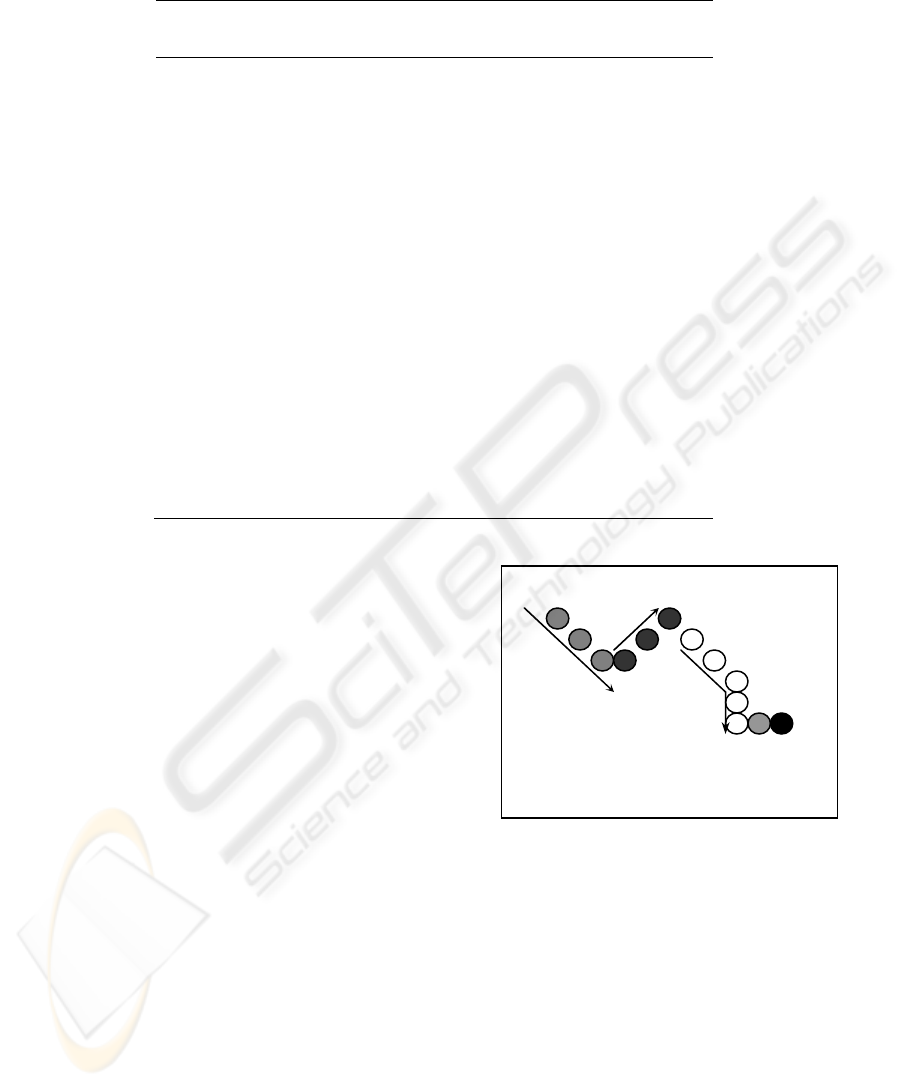
Table 1: A comparative table of mean error, obtained from a uniform criterion of control point selection and the monotonic

way.

It is the description of a function f if ordinate

points

nix

..1, = must be such that:

1..1,

−=<

nixx

. We consider then the border

relation F as a union of piece like curves (graphs)

preserving the monotonic behaviour criterion, i.e.

∪

∈

(2)

where

JjFG

∈∀⊆ , and

}/),(,{

jjjj

fyyxJG

jjj

=∈=

ααα

For convenient sets of index J, J

and restriction

functions

}|{|

Jxj

∈

, such that the next point

following the last of G

is the first one of G

j+1

. G

graphs are correct f

functions descriptions.

Building the G

sets is a very straightforward

operation:

• Beginning with a first point we include the

next one of F.

• As soon as this point doesn’t preserve

monotonic behaviour we begin with a new

j+1

• Processes stop when all F points are

assigned.

Figure 2: Example of an F relation decomposed in graphs

with a correct function description.

In order to avoid building G

reduced to

singletons, as show in figure 2 (G

and G

) the

original F relation may be simplified to preserve

only the first point of constant x ordinate series.

Afterwards, spreading of a constant number of

points is done proportional to the length of the G

and always setting in it is first one.

The point’s choice criterion mentioned before

allows, in two-dimensional interpolation, for taking

account on points where reverse direction changes

take place. Irregularity, of the surface curve, is taken

into account with a sufficient number of

interpolating points, as done in the uniform

Class Mean size

Mean Erro

Unifor

Monotonic

01 2665.6 9.1474 2.0226

02 1885.1067 3.5651 0.43655

03 2657.68 11.0432 5.3732

04 2845.8133 31.6506 2.8447

05 1994.68 1.8569 0.42231

06 2483.04 0.4425 0.71093

07 2365.2667 9.711 0.68609

08 3265.48 0.4753 0.49015

09 2033.2267 19.7583 3.4516

10 2258.2533 3.9345 2.4034

11 1158.9867 5.4739 1.0286

12 1934 1.3393 0.40771

13 1183.4 1.2064 0.39012

14 981.4 0.2752 0.23671

15 3159.08 11.575 8.8491

16 1973.3733 47.4766 6.6833

F = G

∪ G

BIOSIGNALS 2009 - International Conference on Bio-inspired Systems and Signal Processing

464

spreading way. Results on table 1 allows for

comparison between choice of control points with

the criterion motioned before and the uniform one.

Such results show the benefit of choosing control

points with the monotonic criterion instead of the

uniform one.

The 1-D interpolation has been perform using

359 control points, with spline, lineal or closest

interpolated point neighbourhood, depending on the

number of control points present in the decomposed

curve. As a reference at 300 dpi a crayon free hand

trace is about 5 to 6 points wide.

Table 1 also shows size variability of the

different varieties ranging in mean, between 981

pixels for class 14 to 3255 for class 8. With 359

points chosen with the monotonic criterion, all

perimeter point vectors have a standard size and

errors representation is negligible.

Due to perimeter size variability inside a class,

for example in class 15 ranging between 2115 points

to 4276 with a standard deviation of about 521,

coding of (x,y) control perimeter points have been

transformed taking account for size independence.

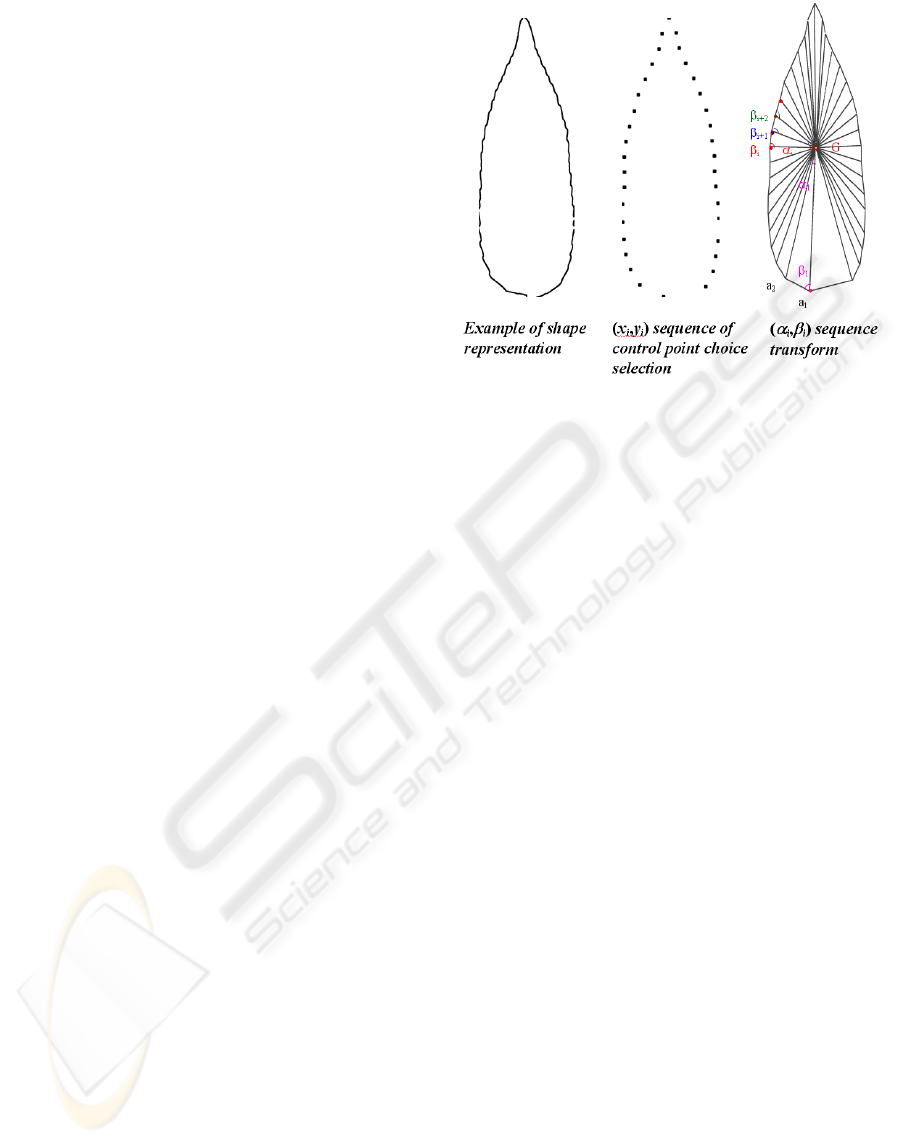
Considering the following definitions:

Γ the set of n, a fixed number, of control points,

)},(/{

..1 iiini

yxXX ==Γ

Where (x

) are point

coordinates of control perimeter points.

the central point of the

set:

),)(/1(

..1..1

∑∑

nini

yxnC

, /

∈

= niii

..1

),(

)(),(

1010 ++

iiiiii

XCXangleXXCangle

angles

defined for each interpolating points of

Γ .

An example is shown in figure 3. Sequences of

) positional points are then transformed in

sequence of

()

, angular points.

The choice of a starting and a central point

accounts for scale and leaf orientation. Placement of

both points sets the scale: its distance separation.

Relative point positioning sets the orientation of the

interpolating shape. Given a sequence of such angles

and

, it’s then possible to reconstruct the

interpolating shape of a leaf. Geometrical properties

of triangle similarities make such sequence size and

orientation free.

4 REDUCTION PARAMETERS

The problem of classification consists on deciding a

class membership of an observation vector (Duda et

al., 2000). Usually this observation vector consists

Figure 3: Example of an angular coding for a 30 control

points selection.

of features that are related. The classification

algorithm has to take a decision after the analysis of

several features even though they can be mutually

related in difficult ways.

The dependencies between the features have an

influence on the learned classifier. It is well known

that there is a relationship between the complexity of

a classifier and the generalization error (Mitchell,

1997).

We propose transforming the input so that the

resulting vector has the property that each

component is independent of the others. We shall do

this by means of ICA. In the case of training a

multilayer perceptron, the inference of the weights is

made by a gradient search, which is known to be

very inefficient if the features are highly correlated

(Duda et al., 2000). It is also known that the

incorrelation pre-processing of the inputs of a

multilayer perceptron improves the convergence of

the algorithm because near a minimum the form of

the error function can be approximated locally by a

hyper-parabola. This explains the improvement that

can be achieved by the use of algorithms such as the

conjugate gradient or the Levenberg-Marquardt.

Notice that the characteristics of these algorithms

are adapted to the fact that the data can have

correlated features. So a process of whitening the

data or using these improvements of the gradient

algorithms means that we are making a strong

hypothesis about the data.

In the past, ICA has been used as a pre-

processing technique for classification (Sanchez-

Poblador et al., 2004), where the authors proposed

the use of the independent component analysis

AUTOMATIC RECOGNITION OF LEAVES BY SHAPE DETECTION PRE-PROCESSING WITH ICA

465

technique for improving the classification rate of

decision trees and multilayer perceptrons. We

propose to follow the same idea to pre-process the

data in such a way that the features will be mutually

independent, and therefore the gradient descent will

follow a smooth surface, even if high order moments

between features are present in the original pattern.

See (Jutten et al., 1991) (Hyvärinen et al., 2001)

for a detailed explanation of ICA theory and

algorithms. In all the experiments the ICA

transformation was done by means of the JADE

algorithm (Cardoso et al., 1996).

5 CLASSIFICATION

An Artificial Neural Network (ANN) can be defined

as a distributed structure of parallel processing,

formed by artificial neurons, interconnected by a

great number of connections (synapses) (see Fig. 4).

Figure 4: General Neural Network structure.

Feed-Forward networks consist of layers of

neurons where the exit of a neuron of a layer feeds

all the neurons on the following layer. The

fundamental aspect of this structure is that feedback

unions do not exist. The so called Multilayer

Perceptron (MLP) is a type of Feed-forward ANN,

where the threshold function is a nonlinear but

differentiable function. This nonlinear differentiable

function is necessary to assure that the gradient can

be calculated, in order to find the good values for all

the parameters of the network.

For the classification system we have used a 2-

layer feed-forward perceptron trained by means of

conjugated gradient descent algorithm (Bishop,

1996), with 50 neurons in the hidden layer and

hyperbolic tangent tanh(.) as a nonlinear function for

these units. The number of input neurons fits in with

the number of components (from 1 to 15), and the

number of output neurons with the number of leaves

classes (16 in our application).

Approximately half of the database (37) was used

in the training process and the rest of the examples

(38) for testing the network.

6 EXPERIMENTS AND RESULTS

We did several experiments in order to find the best

dimension reduction for leaves automatic

recognition. In our experiments we observed that the

first column of each sample, that corresponds to the

interior angles α

are not useful for the classification

purpose. Hence, we use only exterior angles β

To apply ICA to these values we construct a

global matrix with 37 of 75 different samples that

we have for each class, arranged in rows, resulting in

a 592x359 global matrix. ICA algorithm, as detailed

in Section 4, is then applied to this matrix in order to

obtain the projected data by using the subspace

spanned from 5 to 15 independent components (only

odd numbers in our experiment).

Data processed with ICA is used then with a

neural network and results are shown in Table 2. For

each number of components we trained 10 different

networks and we calculated the success of the

classification procedure, showing the success rate

and standard devition value for each case.

We obtained better results compared with these

obtained in (Briceño et al., 2002) where a HMM of

40 stages was used in the best case, giving a success

rate of 78.33% ± 6.06.

With the new ICA pre-processing procedure we

outperform previous results in success rate and we

diminish the variance as well. With 15 independent

components we obtain 80.77% ± 0.29 of success, in

the classification of leaves for 10 different trained

neural networks. The variance in the classification is

strongly diminished from 6.06 for the HMM

(Briceño et al., 2002) to less than 0.80 in all the

cases.

Table 2: Results with MLP classifier.

umber of

Components

Success rate

ICA 5 74.93 % ± 0.75

ICA 7 75.76 % ± 0.62

ICA 9 78.01 % ± 0.55

ICA 11 79.10 % ± 0.51

ICA 13 80.40 % ± 0.78

ICA 15 80.77 % ± 0.29

BIOSIGNALS 2009 - International Conference on Bio-inspired Systems and Signal Processing

466

Also is interesting to observe that with 13

independent components we obtain a very good

result of 80.40% ± 0.78 that outperforms the

previous results showed in (Briceño et al., 2002). As

the number of components is small, we simplify the

classification step.

7 CONCLUSIONS

In this present work, we have presented an

improvement of an automatic leaves recognition

system using Independent Component Analysis and

classifying with multilayer perceptron neural

network. The transformation and reduction of data

contribute to increase its discrimination, from

78.33% using contour parameterization + HMM

(Briceño et al., 2002), to 80.77% using contour

parameterization + ICA + Neural Network.

The advantage of using ICA is twofold: first, we

increase the classification results, specially

diminishing the variance, and second we reduce the

features dimension, giving as a result a less complex

classifier.

Future work will be done exploring other

different ICA algorithms combined with other

classifiers in order to diminish the complexity of the

whole classification system.

ACKNOWLEDGEMENTS

The first author acknowledges support from the

Ministerio de Educación y Ciencia of Spain under

the grant TEC2007-61535/TCM, and from the

Universitat de Vic under the grant R0912.

REFERENCES

Lu, F., Milios, E. E., 1994. Optimal Spline Fitting to

Planar Shape. In Elsevier Signal Processing, No. 37,

pp 129-140.

Loncaric, S., 1998. A Survey of Shape Analysis

Techniques. In Pattern Recognition, Vol. 31 No. 8, pp

983-1001.

Rabiner, L., Juang, B H., 1993. Fundamentals of Speech

Recognition. Prentice Hall, Englewood Cliffs, New

Jersey.

Briceño, J. C., Travieso, C. M., Ferrer, M. A., 2002.

Automatic Recognition of Simple Laurisilva

Canariensis Leaves, by Perimeter Characterization. In

IASTED International Conference on Signal

Processing, Pattern Recognition and its Applications,

pp. 249 – 254.

Burges, C.J.C., 1998. A Tutorial on Support Vector

Machines for Pattern Recognition. In Data Mining and

Knowledge Discovery, Vol. 2, Nº2, pp. 121-167.

Jolliffe I.T., 2002. Principal Component Analysis. Series:

Springer Series in Statistics, Springer, NY 2nd edition.

Jutten, C., Herault, J., 1991. Blind separation of sources,

Part 1: an adaptive algorithm based on neuromimetic

architecture. In Signal Processing (Elsevier), Vol. 24,

Issue 1, pp. 1-10

Hyvärinen, A., Karhunen, J., Oja, E., 2001. Independent

Component Analysis, New York, USA: John Wiley &

Sons.

Duda, R.O., Hart, P.E., Stork, D.G., 2000. Pattern

Classification. Wiley Interscience, 2nd Edition.

Bishop, C., 1996. Neural Networks for Pattern

Recognition. Clarendon, UK: Oxford University Press.

Lu, F., Milios, E.E., 1994. Optimal Spline Fitting to Planar

Shape. In Elsevier Signal Processing No. 37, pp. 129-

140.

Loncaric, S., 1998. A Survey of Shape Analysis

Techniques. In Pattern Recognition. Vol. 31 No. 8,

pp. 983-1001.

Huang, Z., Cohen, F., 1996. Affine-Invariant B-Spline

Moments for Curve Matching. In IEEE Transactions

on Image Processing, Vol. 5. No. 10. pp. 824-836.

Mitchell, T.M., 1997. Machine Learning. McGraw-Hill.

Sanchez-Poblador, V., Monte-Moreno, E., Solé-Casals, J.,

2004. ICA as a preprocessing technique for

Classification. In Independent Component Analysis

and Blind Signal Separation, Lecture Notes in

Computer Science, Springer-Verlag Volume

3195/2004, pp. 1165-1172.

Cardoso, J.F., Souloumiac, A., 1996. Jacobi angles for

simultaneous diagona-lization, In SIAM. Journal

Mathematics Analysis Application, pp. 161-164.

AUTOMATIC RECOGNITION OF LEAVES BY SHAPE DETECTION PRE-PROCESSING WITH ICA

467