COHERENCY AND SHARPNESS MEASURES BY USING ICA

ALGORITHMS

An Investigation for Alzheimer’s Disease Discrimination

Jordi Sol´e-Casals

, Franc¸ois Vialatte

, Zhe Chen

and Andrzej Cichocki

Signal Processing Group, University of Vic, Sagrada Fam´ılia 7, 08500 Vic, Spain

RIKEN Brain Science Institute, LABSP, 2-1 Hirosawa, Saitama, 351-0106 Wako-Shi, Japan

Neuroscience Statistics Research Lab., Dept. of Brain and Cognitive Sciences, MIT, Cambridge, MA 02139, U.S.A.

Keywords:

EEG, Alzheimer disease, ICA, BSS, Feature extraction.

Abstract:

In this paper, we present a comprehensive study of different Independent Component Analysis (ICA) algo-

rithms for the calculation of coherency and sharpness of electroencephalogram (EEG) signals, in order to

investigate the possibility of early detection of Alzheimer’s disease (AD). We found that ICA algorithms can

help in the artifact rejection and noise reduction, improving the discriminative property of features in high fre-

quency bands (specially in high alpha and beta ranges). In addition to different ICA algorithms, the optimum

number of selected components is investigated, in order to help decision processes for future works.

1 INTRODUCTION

Alzheimer’s disease (AD) is the most prevalent form

of neuropathology leading to dementia; it affects ap-

proximately 25 million people worldwide and is ex-

pected to have a fast recrudescence in the near future

(Ferri et al., 2006). Numerous clinical methods that

are now available to detect this disease include brain

imaging (Alexander, 2002), (Deweer et al., 1995), ge-

netic studies (Tanzi and Bertram, 2001), and other

physiological markers (Andreasen et al., 2001). How-

ever, these methods cannot be employed for the mass

screening of a large population. A combination of

psychological tests, such as Mini-mental score eval-

uation (MMSE), with electrophysiological analysis

(e.g. electroencephalogramorEEG), wouldbe a more

efﬁcient and inexpensive screening approach for de-

tecting elderly subjects affected by AD.

The purpose of this study is to make quantita-

tive comparisons of different independent component

analysis (ICA) algorithms and to investigate their po-

tential efﬁciency for preprocessing (such as noise re-

duction and feature extraction) the EEG data. The ob-

jective is to improve the discrimination between AD

patients and age-matched control subjects.

2 EXPERIMENTAL DATA

In the course of a clinical study, mutlichan-

nel EEG measurements (Deltamed EEG machine)

were recorded from 37 elderly patients affected by

Alzheimer’s disease with a clinical follow-up treat-

ment (labeled AD set) as well as from 39 age-matched

controls (labeled Control set). The electrodes were lo-

cated on 19 sites according to the 10-20 international

system. Reference electrodes were placed between

Fz and Cz, and between Cz and Pz. The sampling

frequency was 256 Hz, with bandpass ﬁlter 0.17-100

Hz. When possible, three periods of 5 seconds were

selected in a ”rest eyes-closed” condition for each

patient—only 4 subjects from the Alzheimer group

did not allow us to extract three 5-second sessions and

therefore were discarded in the current study. Hence,

two groups of three 5-second signals were obtained

for each of the 39 Controls, and 33 AD. The three in-

dependent sessions were chosen so as to minimize the

presence of artifacts.

468

Solé-Casals J., Vialatte F., Chen Z. and Cichocki A. (2009).

COHERENCY AND SHARPNESS MEASURES BY USING ICA ALGORITHMS - An Investigation for Alzheimer’s Disease Discrimination.

In Proceedings of the International Conference on Bio-inspired Systems and Signal Processing, pages 468-475

DOI: 10.5220/0001430904680475

 SciTePress

3 INDEPENDENT COMPONENT

ANALYSIS AND BLIND

SOURCE SEPARATION

3.1 Data Model

The experimental data are assumed to be generated by

a probabilistic generative model that is described by

two equations as follows:

= µ+ Bz

+ ε

, (1)

= As

, (2)

where t denotes the time index. Equation (1) is es-

sentially a factor analysis (FA) model, where z ∈ R

are the hidden variables called “factor”; the m×n ma-

trix B is called the “loading matrix”; x

∈ R

denote

the observed multi-channel signals measured in the

electrodes; µ ∈ R

denotes the constant mean vector

that is often assumed to zero; and ε

∈ R

denotes the

additive uncorrelated noise that corrupts the measure-

ments. The equation (2) describes a linear mixture

model that is related to the blind source separation

(BSS) problem of our interest that will be discussed

later, where s ∈ R

denote the independent source

signals originated from the brain; A denotes a lin-

ear mixing matrix that models the mixing process and

the stationary propagation or scattering effect within

a short timescale; and the mixed signals consist of the

hidden factor z obtained in (1). Here, we assume a

square mixing/demixing setting, in which m > n = N.

3.2 Procedure

At the ﬁrst stage, we apply principal factor analysis

or principal component analysis (PCA) to perform di-

mensionality reduction. This is done by whitening the

hidden factor z

given x

, assuming that noise ε

is un-

correlated.

Speciﬁcally, given observed samples {x

}

t=1

, we

can calculate the sample covariance matrix (assuming

zero mean) and conduct its eigenvalue decomposition

(EVD) as follows

∑

t=1

= UΛU

, (3)

where U is the m× m orthogonal matrix that consists

of eigenvectors as its column vectors, Λ is a diagonal

matrix that consists of the diagonal entries as eigen-

values. Let U

denote an m× n matrix that consists

of the ﬁrst n dominant eigenvectors, then we can esti-

mate the noise covariance by

Σ =

− U

, (4)

and the loading matrix by

B = U

1/2

. (5)

Finally, the whitened factor variable z is produced by

a linear transformation

= Qx

, (6)

where Q = (

−1

At the second stage, an ICA algorithm is imple-

mented to perform BSS. Speciﬁcally, given z

, we in-

tend to ﬁnd an optimal demixing matrix W, operated

on the whitened signal by y

= Wz

, such that the

components in y

are mutually uncorrelated or inde-

pendent. The estimated output signal y

are assumed

to be the source signals of interest up certain scaling

and permutation ambiguity.

Upon PCA and ICA stages, we can apply a

deﬂation procedure to identify the individual orig-

inal source in the sensor space by backward pro-

jection. Speciﬁcally, given the output signal y

(t),y

(t),... ,y

(t)]

, we can also reconstruct the

incomplete hidden factor by projecting the ith compo-

nent of y

, denoted by y

(t), backward onto the sub-

space

= W

−1

[0,... , 0,y

(t),0,... , 0]

≡



−1



(t), (7)

where



−1



denotes the ith column vector of

the matrix W

−1

. Furthermore, we can reconstruct the

speciﬁc source of interest in the observed data space

(i.e., the scalp signals contributed merely to the ith

source)

= Q

†

= Q

†

−1

[0,.. ., 0,y

(t),0,.. .,0]

= (WQ)

†

[0,.. ., 0,y

(t),0,.. ., 0]

, (8)

where Q

†

denotes the pseudoinverse of matrix Q.

Hence, by projecting

to the original channels’ posi-

tions, we essentially identify the source(s) of interest.

In addition, if we are only interested in denois-

ing or getting rid of a speciﬁc component, we can

set that speciﬁc output signal (say y

) to zero while

keeping other components intact, and apply the same

above-described back projection procedure to recover

the original scene. In our experiments, by ranking

the output components, we always select the one that

has the least absolute kurtosis value (i.e., the one

close to Gaussian by assuming zero kurtosis statis-

tic for Gaussian signal, positive kurtosis statistic for

super-Gaussian signal, and negative kurtosis for sub-

Gaussian signal).

COHERENCY AND SHARPNESS MEASURES BY USING ICA ALGORITHMS - An Investigation for Alzheimer's

Disease Discrimination

469

3.3 Selection of CANDIDATE

ALGORITHMS

For comparison, we have selected eight representative

ICA algorithms.

The selection criteria for these algorithms are

based on several factors: (i) computationally efﬁ-

ciency; (ii) robustness; (iii) fewer degree of freedom

(such as the choices of learning rate parameter, non-

linearity, or number of iterations); (iv) preference to

batch method.

Speciﬁcally, the following eight ICA/BSS algo-

rithms are among some of the most popular BSS

methods in the literature. A brief description and con-

ﬁguration setup of each method is given below:

1. AMUSE (Algorithm for Multiple Unknown Sig-

nals Extraction)(Tong et al., 1991): A second-

order batch BSS algorithm based on a two-stage

eigenvalue decomposition.

2. SOBI (Second-Order Blind Identiﬁcation) (Be-

louchrani et al., 1997): A second-order batch BSS

algorithm based on joint diagonalization of time-

delayed signal covariance matrices. In our exper-

iments, the number of time-delay covariance ma-

trices is set to be 30.

3. JADE (Joint Approximate Diagonalization of

Eigen-matrices) (Cardoso and Souloumiac,

1993): A high-order statistics (HOS)-based

ICA algorithm based on joint diagonalization

of second- and fourth-order cross-cummulants.

As a batch method, JADE algorithm requires no

parameter tuning; however, it is computationally

expensive and memory-storage demanding (with

an order of O (n

)).

4. Pearson-ICA (Karvanen et al., 2000): An itera-

tive ICA algorithm based on Pearson system; the

maximum number of iterations is set to be default

value, 1000.

5. FastICA (Hyvarinen and Oja, 1997): A ﬁxed-

point ICA method for sequential source extrac-

tion, the ﬁxed point is sought by maximizing the

“negentropy” of each mixture. We used default

parameter setup with

tanh

nonlinearity and max-

imum number of iterations as 1000.

6. Thin-ICA : (Cruces-Alvarez et al., 2004): A batch

ICA algorithm for simultaneous blind signal ex-

traction based on thin QR and SVD factorizations.

The selection of the ICA algorithms here is by no

means exhaustive and it mainly reﬂects our preference cri-

teria. For instance, some iterative ICA algorithms like Info-

max or natural gradient were not chosen here because they

typically have slow convergence speed.

7. CCA-BSS (Canonical Correlation Analysis-based

BSS) (Borga and Knutsson, 2001): A second-

order BSS algorithm based on canonical correla-

tion of temporal observations.

8. TFD-BSS (Time-Frequency Distribution Joint

Diagonalization-based BSS) (F´evotte and Don-

carli, 2004): This method takes account of infor-

mation in time and frequency and the source sep-

aration criterion is conducted in time-frequency

domain based on joint diagonalization of the spa-

tial time-frequency distribution.

The detailed description of algorithms are beyond

the scope here; for relevant references, see (Cichocki

and Amari, 2002). All of algorithms are implemented

in MATLAB, some of them are available for down-

load from the original contributors or in the ICALAB

package (Cichocki et al., WWW).

For each algorithm, we have varied the number of

independent components extracted (namely, n), from

3 to 10, and searched for the optimum within this

range. It was found that almost all algorithms con-

verge within our experimental setup, except for the

FastICA algorithm which sometimes failed to con-

verge; in which cases FastICA was excluded from the

comparisons.

4 PERFORMANCE EVALUATION

4.1 Coherency

Coherency is an informative measure that character-

izes how the phases of two time series (in our cases,

two electrodes’ recordings) are coupled to each other,

hence it was often used for measuring interactions of

two signals. Coherency or coherence is also closely

related to the terms “phase locking” and “phase syn-

chrony” that were proposed in the literature. Interest-

ingly, Coherence is often viewed as an important mea-

sure for distinguishing AD and MCI in EEG analysis

of clinical practice (Koenig et al., 2005), (Babiloni

et al., 2006).

In consistent with the terminology in Nolte et al.

(2004), given two electrodes’ recordings x

(t) and

(t), let X

(ω) and X

(ω) denote their corresponding

Fourier transforms; then the coherency between x

(t)

and x

(t) is deﬁned as the normalized cross-spectrum

(ω) =

(ω)

(ω)S

j j

(ω)

, (9)

where S

(ω) =



(ω)X

∗

(ω)



denotes the cross-

spectrum, and





represents the expectation average.

BIOSIGNALS 2009 - International Conference on Bio-inspired Systems and Signal Processing

470

Averaged alpha−range (8−12 Hz) coherence of AD patients

5 10 15

0.5

0.55

0.6

0.65

0.7

0.75

0.8

0.85

0.9

0.95

Averaged alpha−range (8−12 Hz) coherence of control subjects

5 10 15

18 0.5

0.55

0.6

0.65

0.7

0.75

0.8

0.85

0.9

0.95

Figure 1: The mean alpha-range (8-12 Hz) coherence with

raw EEG recordings (Left) averaged over all 33 AD pa-

tients, and (Right) averaged over all 39 control subjects.

And coherence is deﬁned as the absolute value (or

the magnitude) of the coherency, namely, Coh

(ω) =

(ω)|.

In measuring the total coherence across the 19

electrodes, we are interested in comparing the “aver-

aged coherence” of the original raw EEG recordings

and that of the ICA-processed signals (by discarding

one Gaussian-like component with the least absolute

kurtosis statistic). The values of mutual coherence be-

tween electrodes are stored in a 19-by-19 symmetric

matrix, with diagonal values being unity.

Speciﬁcally, we pay special attention to the alpha-

range (8-12 Hz) coherence. The reasons for choosing

the alpha-range are twofold: (i) The alpha wave is less

noisy and therefore more reliable in the EEG record-

ings (because the subjects were all in rest conditions);

(ii) The alpha-coherence is believed to a useful mea-

sure in characterizing AD subjects (Babiloni et al.,

2006). Figure 2 illustrates the averaged alpha-range

coherence (displayed in a 19-by-19 matrix) among

all 33 AD patients using the raw EEG recordings.

As seen in the ﬁgure, typically, neighboring channels

have relatively high coherence values.

4.2 Spatial Sharpness Measure for ICA

Sources

After ICA source extraction, components are obtained

which are hoped to be representative of independent

brain activities. However, all mathematical methods

rely on mathematical assumptions and criteria which

are not necessarily realistic in a real-world setting.

Therefore we are also interested in investigating the

biological plausibility of the ICA components.

One way to assess the plausibility of ICA com-

ponents is to observe their spatial distribution—since

brain activity arises from a speciﬁc area and then

spreads over a larger region in the brain. During a

given short time interval, it is likely that brain activ-

ity shall be located in delimited areas. After apply-

ing ICA and back-projecting the components, each

three situations can be observed for each source dur-

ing short time windows:

1. The source is spatially delineated in a localized

and peaky area.

2. The contributing electrodes are spread all over the

scalp without peaks.

3. The source is a combination of more than one

peak in several separated locations.

The ﬁrst situation is the only one that could be plau-

sibly attributed to brain activity – note that sources

representative of known EEG artifacts are also often

spatially delineated, with a very sharp location (De-

lorme et al., 2001) – so that ICA algorithms extracting

spatially sharp sources will provide good information

both for brain signal analysis, and for artifact rejec-

tion. The second situation is the worst scenario: such

a source is very unlikely to be attributed to brain ac-

tivity, and would not be easily construed. The third

situation is also unlikely to be representative of brain

activity, and probably accounts for several indepen-

dent activities which were not accurately separated by

the ICA algorithm.

Naturally, we would need a measure that charac-

terizes the “peakiness” of a distribution in a 2D repre-

sentation of the scalp. Ideally, this measure shall keep

the 2D structural information (note that 2D peak and

2D scrambled peak are not the same distributions),

therefore the standard kurtosis measure for 1D signal

is not suitable. Furthermore, this measure should re-

ject the cases where the 2D distribution has multiple

peaks.

To measure the spatial sharpness (or sparseness)

of the extracted independent components, we conduct

the following two-step procedure.

1. Gaussian smoothing

2. Calculating the kurtosis statistic of the Gaussian

smoothed matrix

In the ﬁrst step, after removing the source that has

the least absolute kurtosis value (representing close-

to-Gaussian noise), we extract the 2D topological in-

formation of each source. To this end we apply a bi-

dimensional Gaussian smoothing procedure (Gonza-

lez and Woods, 1992). In our case, with a small num-

ber of electrodes, we represent the spatial information

of each source with a matrix of spatial source distribu-

tion D, an ℓ

× ℓ

matrix (in our case, it is a 5× 5 ma-

trix reﬂecting the electrode layout, unused border po-

sitions are set to zero to obtain a square matrix). For

each source, we convolve the matrix D with a Gaus-

sian kernel G. G is a 2D isotropic Gaussian distri-

bution discretized over a square matrix whose dimen-

sion is d, with d = max(ℓ

,ℓ

), and whose standard

deviation σ = (d−1)/2 such that 2σ encompasses the

COHERENCY AND SHARPNESS MEASURES BY USING ICA ALGORITHMS - An Investigation for Alzheimer's

Disease Discrimination

471

a1) Peaky distribution

2 4 6 8 10

a2) Gaussian smoothing

5 10 15

0 0.02 0.04

100

150

200

250

300

a3) Kurtosis = 11.4

b1) Random distribution

2 4 6 8 10

b2) Gaussian distribution

5 10 15

0 0.02 0.04

100

150

b3) Kurtosis = −0.6

c1) Abnormal distribution (2 peaks)

2 4 6 8 10

c2) Gaussian distribution

5 10 15

0 0.02 0.04

100

150

200

250

c3) Kurtosis = 4.2

Figure 2: Illustrations of the kurtosis measure to Gaussian

smoothed matrixes.

whole matrix D:

G(x,y) =

2πσ

2σ

(10)

The smoothed matrix O is obtained by convolving

the Gaussian kernel G and the spatial distribution of

the source D:

O(x,y) =

∑

i=1

∑

j=1

G(k,l)D(x− i,y− j) (11)

This matrix has interesting properties for our purpose:

for “ﬂattened” D, the smoothed matrix O remains ﬂat.

For peaky D, the smoothed matrix remains peaky;

see Figure 2 for an illustration. For multiple peaks,

the smoothed matrix’s peaks are ﬂattened. Therefore,

matrix O roughly represents the spatial distribution

information we are interested in extracting.

After the spatial informationhas been extracted by

smoothing, the sparseness is computed in the second

step using the conventional kurtosis measure. At this

step the 2D spatial distribution does not matter any-

more, therefore the kurtosis measure becomes well

suited. Finally we obtain a single spatial sharpness

measure for each source s, denoted by κ

(sparseness

of the smoothed matrix), using the kurtosis excess

(Kenney and Keeping, 1962) for the matrix O

(which

represents the smoothed back-projected matrix from

the source s):

)

− 3, (12)

where µ

) and µ

) are the second and fourth

order moments of the elements of O

The absolute value of the measure κ

is close to

zero for “ﬂat distributed” elements in the matrix D

(see second row illustration in Figure 2). On the

other hand, the measure κ

is highest when there is

only one peak, and the measure value decreases when

more peaks appear. After calculating this measure for

each source (except for the rejected one), the averaged

absolute value is used as an indicator of the spatial

sharpness for all the sources

κ =

∑

s=1

|κ

|. (13)

This value will be also averaged within a moving tem-

poral window across the complete duration of the data

(explained later in experimental section).

5 EXPERIMENTAL RESULTS

5.1 Comparison on Coherence Change

We back projected the ICA components (by discard-

ing only one component with the least absolute kur-

tosis statistic) to the original 19 electrodes. By com-

paring the original coherence matrix, we can calculate

the relativepositive increase of alpha-rangecoherence

as well as the relative decrease of alpha-range coher-

ence; they are summed over and then averaged over

the total number of subjects and the counted number

of electrodes (each with increased or decreased coher-

ence value) based on 5 seconds of EEG recordings.

In total, for each ICA algorithm with one speciﬁc

number of n (i.e., the number of independent compo-

nents), we calculate two statistics (mean±STD), one

pair for the averaged coherence increase, and another

pair for the averaged coherence decrease. The same

procedure is applied to each independent session of

EEG recordings. The mean statistics of averaged co-

herence increase and averaged coherence decrease are

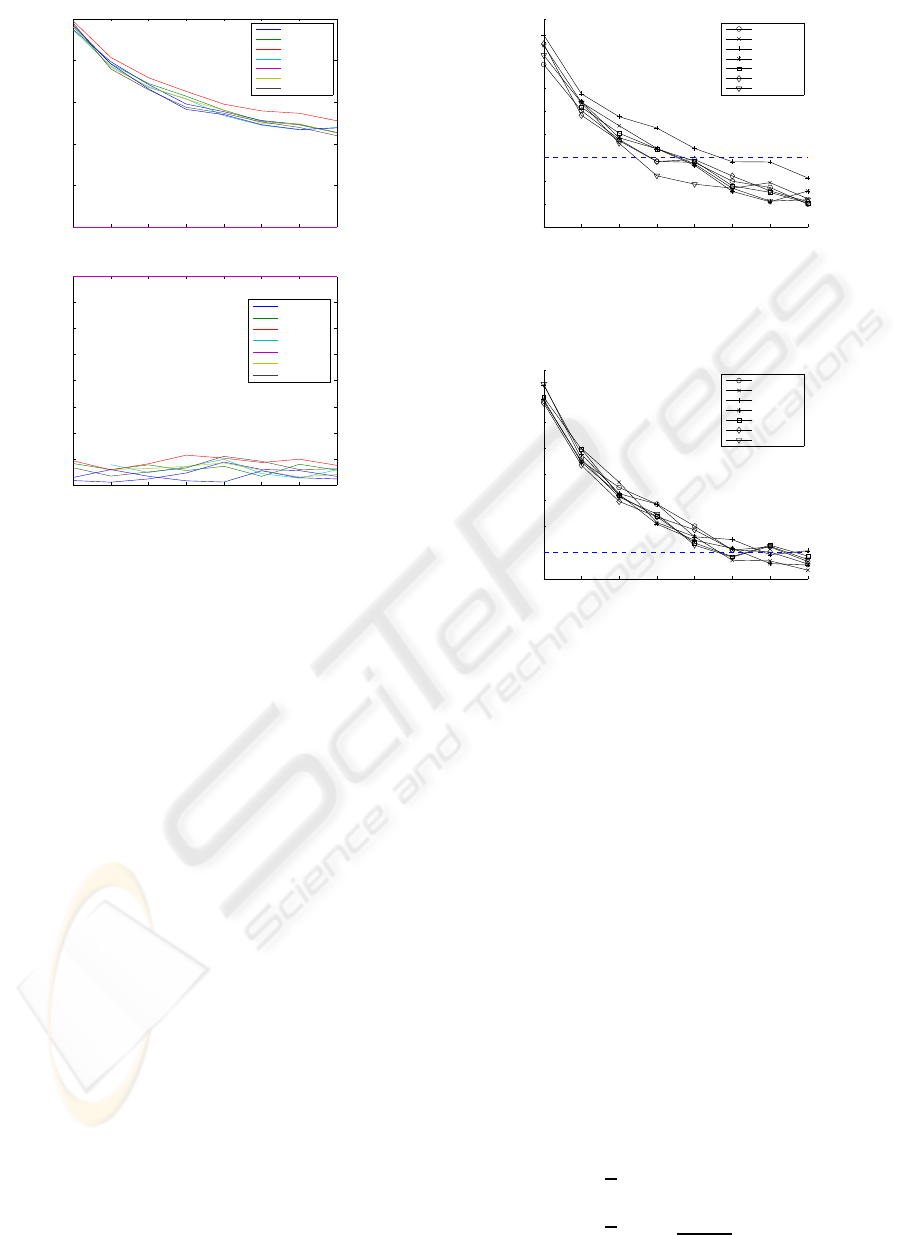
shown in Figure 3. As seen in the ﬁgure, for all ICA

algorithms, the relative (averaged) coherence increase

values drop down as the number of independent com-

ponents increase, whereas the relative (averaged) co-

herence decrease values remain approximately con-

stant regardless of the number of independent com-

ponents. However, the overall positive coherence in-

crease is much greater than the overall negative co-

herence decrease, thereby resulting a net increase of

coherence for all channels. This phenomenon is an-

ticipated because the employed PCA/ICA procedure

essentially discard the noise components and keep the

other components intact; on the other hand, the effect

of noise reduction (and therefore coherence increase)

is more pronounced when the reduced dimensionality

is signiﬁcant (i.e., with a small number of independent

components). It is also noted that although Figure 3

only illustrates the result of the EEG recordings in one

session, similar phenomena were also found in other

two sessions.

BIOSIGNALS 2009 - International Conference on Bio-inspired Systems and Signal Processing

472

3 4 5 6 7 8 9 10

0.05

0.1

0.15

0.2

0.25

Number of independent components

Averaged coherence increase

AMUSE

SOBI

JADE

Pearson−ICA

thin−ICA

CCA−BSS

TFD−BSS

3 4 5 6 7 8 9 10

−0.16

−0.14

−0.12

−0.1

−0.08

−0.06

−0.04

−0.02

Number of independent components

Averaged coherence decrease

AMUSE

SOBI

JADE

Pearson−ICA

thin−ICA

CCA−BSS

TFD−BSS

Figure 3: Top panel: performance comparison of averaged

alpha-range coherence increase (mean statistics). Bottom

panel: performance comparison of averaged alpha-range

coherence decrease (mean statistics). The comparison was

made between 7 ICA algorithms (excluding FastICA) on

AD subjects.

Using averaged positive coherence increase value

as an indicator of efﬁciency, by comparing different

ICA/BSS algorithms, it was found that the JADE al-

gorithm is the best, followed by two second-order

statistic based ICA algorithms: SOBI and CCA-BSS.

Interestingly, all of these three algorithms exploit in-

formation of temporal correlation, and two second-

order ICA/BSS algorithms are very computationally

efﬁcient (compared to others except for AMUSE). By

summing together the averaged relative coherence in-

crease and the averaged relative coherence decrease,

we obtain the result shown on Figure 4. In this case,

JADE algorithm remains the best in achieving the

highest net increased coherence, followed by SOBI

and thin-ICA. As seen in the ﬁgure, in order to obtain

net positive alpha-range coherence change, an opti-

mum number of independent components is around

5 or 6. Interestingly, this number is consistent with

other earlier investigations using the same EEG data

set (Sol´e-Casals et al., 2008) (Cichocki et al., 2005)

(Vialatte et al., 2005).

Likewise, for the control subjects, we can conduct

the same analysis; the performance comparison of av-

erage net alpha-range coherence between seven ICA

algorithms is shown in Figure 5. It seems that the

3 4 5 6 7 8 9 10

−0.06

−0.04

−0.02

0.02

0.04

0.06

0.08

0.1

0.12

Number of independent components

net change of coherence

AMUSE

SOBI

JADE

Pearson−ICA

thin−ICA

CCA−BSS

TFD−BSS

Figure 4: Performance comparison of averaged net alpha-

range coherence change between 7 ICA algorithms (exclud-

ing fastICA) on AD subjects.

3 4 5 6 7 8 9 10

−0.02

0.02

0.04

0.06

0.08

0.1

0.12

0.14

Number of independent components

net change of coherence

AMUSE

SOBI

JADE

Pearson−ICA

thin−ICA

CCA−BSS

TFD−BSS

Figure 5: Performance comparison of averaged net alpha-

range coherence change between 7 ICA algorithms (exclud-

ing fastICA) on control subjects.

ICA component threshold for attaining positive co-

herence is slightly increased to around 7 or 8. This

also implies that the EEG recordings of the AD sub-

jects are less coherent than those of the control sub-

jects because there are more source componentsin the

recorded signals.

5.2 Comparison on the Spatial

Sharpness Measure

When the spatial sharpness measure is applied to

ICA components, the time evolution of the compo-

nent has to be taken into account: it is not unlikely

that a brain activity may ﬂow from one brain area

to another area. We used overlapping shifted time-

windows of w=500 msec over the total T=5 seconds,

and measured the spatial power distribution of the

back-propagatedsource on the scalp at each time step.

At each step, a sharpness measure value κ is obtained

for each source, the ﬁnal result will be given by the

average sharpness

κ:

κ =

T−w

∑

t=1

κ(t, w)

T − w

(14)

COHERENCY AND SHARPNESS MEASURES BY USING ICA ALGORITHMS - An Investigation for Alzheimer's

Disease Discrimination

473

3 4 5 6 7 8 9 10

4.5

5.5

6.5

Nb component

source spatial peaknes

Figure 6: Relation between the number of components ex-

tracted and the average sharpness κ

of the sources. Stars

represents average for all algorithms, error bars represents

the standard deviation for all algorithms.

where κ(t,w) is the smoothed kurtosis for the source

from time t to time t + w.

In order to obtain a fair comparison, we select the

AD patients (33 subjects) as the experimental data

since it was found that these recordings have gener-

ally poorer signal-to-noise ratio (SNR) than the con-

trol subjects. For each patient, three sessions of 5 sec-

onds are used. For each session, the median value of

33 sharpness measure values for each patient is re-

trieved. This median value yields the representative

value of sharpness for a given session. Since we are

interested in a generally well-suited algorithm, and

the goal is to search for the most consistent results,

the ﬁnal indicator will be given by the average κ

each session:

+ κ

, N ∈ [3,10] (15)

where N denotes the number of selected components,

and κ

,κ

denote the value κ

for sessions 1,

2, and 3, respectively. The value κ

is computed for

each algorithm, and for all possible numbers (3∼10)

of components.

Figure 6 displays the overall result obtained from

this indicator. The straight line is obtained by a lin-

ear least square regression, showing a linear increase

(Pearson R

= 0.74, p < 0.05). Therefore, the more

sources are extracted, the more spatially sharp solu-

tion is obtained. Standard deviation of κ

over the

ICA algorithms is best for 5 to 7 components: within

this range all ICA algorithms produce similar results,

which indicates that the underlined true number of

sources is likely to be close to this range.

When taken independently, each algorithm does

not show the same performance. Figure 7 represents

the distributions of κ

for all algorithms. The overall

increasing reported in Figure 6 is visible, as well as

the consistency over components 5 to 7.

According to this measure, the overall winner is

ThinICA and the overall worst algorithm is TFBSS.

When analyzing the most stable period (5 to 7 compo-

nents),the best algorithms, in decreasing order of ef-

ﬁciency, would be CCABSS, ThinICA, AMUSE and

JADE.

3 4 5 6 7 8 9 10

4.3

4.7

5.3

5.7

Nb component

sources spatial peaknes

AMUSE

SOBI

JADE

Pearson ICA

ThinICA

CCABSS

TFBSS

Figure 7: Spatial sharpness k

of the sources, depending

on the chosen algorithm. Sharpness is reported using the

overall median kurtosis measure presented above. Except

for ThinICA, for 3 components the results are poor; in gen-

eral, the best algorithm depends on the selected number of

components.

6 CONCLUSIONS

In this paper, we have proposed several measures or

criteria to compare several popular ICA algorithms

in an investigation of feature extraction of EEG sig-

nals for the purpose of discriminating Alzheimer’s

disease. As a powerful signal processing tool used

in the preprocessing step, ICA was found useful in

artifact rejection, improving SNR, and noise reduc-

tion, all of which are important for feature selection

at the later stage. We also investigate the neurophys-

iological plausibility of the ICA outputs in terms of

the sharpness measure.

It was found that, in general, ICA algorithms

are particularly useful for feature extraction in high

frequency bands, especially in high alpha and beta

ranges; in contrast, in low-frequency bands, little gain

has been obtained compared to the baselines. This

fact is more or less anticipated, because EEG signals

are usually contaminated by noise at high-frequency

bands, but are more resistant to noise at low frequency

bands. Moreover, the optimum number of selected

components seem to depend on the selected algo-

rithms, but the overall observations seem to indicate

the number should be in the range from 4 to 7. In

terms of the overall average performance, it seem that

the JADE, SOBI, thinICA, and CCABSS algorithms

give more consistent and better results.

ACKNOWLEDGEMENTS

First autor acknowledges support from the Ministe-

rio de Educaci´on y Ciencia of Spain under the grant

TEC2007-61535/TCM, and from the Universitat de

BIOSIGNALS 2009 - International Conference on Bio-inspired Systems and Signal Processing

474

Vic under the grant R0912.

REFERENCES

Alexander, G. E. (2002). Longitudinal pet evaluation of

cerebral metabolic decline in dementia: A poten-

tial outcome measure in alzheimer’s disease treatment

studies. In American Journal of Psychiatry, vol. 159,

pp. 738-745.

Andreasen, N., Minthon, L., Davidsson, P., Vanmechelen,

E., and et al. (2001). Evaluation of csf-tau and csf-a?2

as diagnostic markers for alzheimer disease in clinical

practice. In Am Med Assoc, vol. 58, pp. 373-379.

Babiloni, C., Ferri, R., Binetti, G., Cassarino, A., Forno,

G. D., Eercolani, M., Ferreri, F., Frisoni, G., and et al.

(2006). Fronto-parietal coupling of brain rhythms in

mild cognitive impairment: A multicentric eeg study.

In Brain Research Bulletin, pp. 63–67.

Belouchrani, A., Abed-Meraim, K., Cardoso, J.-F., and

Moulines, E. (1997). A blind source separation tech-

nique using second-order statistics. In IEEE Trans.

Signal Processing, vol. 45, pp. 434–444.

Borga, M. and Knutsson, H. (2001). A canonical correla-

tion approach to blind source separation. In Technical

Report LiU-IMT-EX-0062, Department of Biomedical

Engineering.

Cardoso, J. F. and Souloumiac, A. (1993). Blind beam-

forming for non-gaussian signals. In IEE Proceedings

- Part F, 140, 362–370.

Cichocki, A. and Amari, S. (2002). Adaptive Blind Signal

and Image Processing. Wiley, New York.

Cichocki, A., Amari, S., Siwek, K., and

et al., T. T. (WWW). Icalab toolboxes.

http://www.bsp.brain.riken.jp/ICALAB.

Cichocki, A., Shishkin, S. L., Musha, T., Leonowicz, Z.,

Asada, T., and Kurachi, T. (2005). Eeg ﬁltering based

on blind source separation (bss) for early detection

of alzheimer’s disease. In Clinical Neurophysiology,

116, pp. 729–737.

Cruces-Alvarez, S. A., Cichocki, A., and Lathauwer, L. D.

(2004). Thin qr and svd factorizations for simultane-

ous blind signal extraction. In Proc. European Signal

Processing Conference (EUSIPCO), Vienna, Austria,

pp. 217–220.

Delorme, A., Makeig, S., and Sejnowski, T. (2001). Auto-

matic artifact rejection for eeg data using high-order

statistics and independent component analysis. In 3rd

ICASSP International Workshop, San Diego,.

Deweer, B., Lehericy, S., Pillon, B., Baulac, M., and et al.

(1995). Memory disorders in probable alzheimer’s

disease: the role of hippocampal atrophy as shown

with mri. In British Medical Journal, vol. 58, p. 590.

Ferri, C. P., Prince, M., Brayne, C., and et al., H. B. (2006).

Global prevalence of dementia: a delphi consensus

study. In The Lancet, vol. 366, pp. 2112-2117.

F´evotte, C. and Doncarli, C. (2004). Two contributions to

blind source separation using time-frequency distribu-

tions. In IEEE Signal Processing Letters, 11, pp. 386–

389.

Gonzalez, R. and Woods, R. (1992). Digital Image Process-

ing. Addison-Wesley.

Hyvarinen, A. and Oja, E. (1997). A fast ﬁxed-point algo-

rithm for independent component analysis. In Neural

Computation, 9(7) pp. 1483–1492.

Karvanen, J., Eriksson, J., and Koivunen, V. (2000). Pear-

son system based method for blind separation. In

Workshop on Independent Component Analysis and

Blind Signal Separation, ICA2000, Helsinki, pp. 585–

590.

Kenney, J. F. and Keeping, E. S. (1962). Mathematics of

Statistics. Part 1. Van Nostrand, Princeton, NJ.

Koenig, T., Prichep, L., Dierks, T., Hubl, D., Wahlund, L.,

John, E., and Jelic., V. (2005). Decreased eeg synchro-

nization in alzheimer’s disease and mild cognitive im-

pairment. In Neurobiology of Aging, 26, pp. 165–171.

Sol´e-Casals, J., Vialatte, F., and Cichocki, Z. C. A. (2008).

Investigation of ica algirithms for feature extraction of

eeg signals in discrimination of alzheimer disease. In

Proc. International Conference on Bio-Inspired Sys-

tems and Signal Processing, Biosignals, pp. 232–235.

Tanzi, R. E. and Bertram, L. (2001). New frontiers in

alzheimer’s disease genetics. In Neuron, vol. 32, pp.

181-184.

Tong, L., Soon, V., Huang, Y. F., and Liu, R. (1991). Inde-

terminacy and identiﬁability of blind identiﬁcation. In

IEEE Trans. CAS, vole. 38, pp. 499–509.

Vialatte, F., Cichocki, A., Dreyfus, G., Musha, T.,

Rutkowski, T., and Gervais, R. (2005). Blind source

separation and sparse bump modelling of time fre-

quency representation of eeg signals: New tools for

early detection of alzheimer’s disease. In Proc. IEEE

Workshop on Machine Learning for Signal Process-

ing, pp. 27–32.

COHERENCY AND SHARPNESS MEASURES BY USING ICA ALGORITHMS - An Investigation for Alzheimer's

Disease Discrimination

475