MAPPING LANDMARKS ON TO THE FACE

G. M. Beumer, R. N. J. Veldhuis and B. J. Boom

Signals and Systems Group, University of Twente, P.O. Box 217 7500 AE, Enschede, The Netherlands

Keywords:

Landmarking, Face recognition, Biometrics.

Abstract:

Landmarking can be formalised as calculating the Maximum A-posteriori Probability (MAP) of a set of land-

marks given an image (texture) containing a face. In this paper a likelihood-ratio based landmarking method

is extended to a MAP-based landmarking method. The approach is validated by means of experiments. The

MAP approach turns out to be advantageous, particularly for low quality images, in which case the landmark-

ing accuracy improves signiﬁcantly.

1 INTRODUCTION

An important prerequisite for reliable face recogni-

tion is that the face is registered prior to recognition.

Registration is the alignment of the face to a ﬁxed

position, scale and orientation. Registration in face

recognition is usually based on landmarks, which are

stable points in the face that can be found with sufﬁ-

cient accuracy, e.g. the eyes. A reliable method for

automatic landmarking and registration is essential

for the automatic face recognition. The accuracy of

the landmarking has been shown to have a strong re-

lation to the recognition result (Beumer et al., 2005).

Work on landmarking includes, amongst others,

(Everingham and Zisserman, 2006), in which the

authors compare a regression method, a Bayesian

method, and ﬁnally a discriminative method for land-

marking. Work by (Cristinacce and Cootes, 2006) fo-

cuses on both multiple templates of the landmark and

the landmark coordinates to constrain the search area.

The above approaches do not explicitly use the proba-

bility of the landmark coordinates. In this paper these

will be exploited by extending a method based on a

log likelihood ratio to a Maximum A-posteriori Prob-

ability (MAP) approach (van Trees, 1968).

In (Bazen et al., 2003) image data at each posi-

tion in a region of interest is compared to a landmark

template by a log-likelihood ratio based detector. The

position at which the log-likelihood ratio is highest

is taken as the position of the landmark. This ap-

proach has been further developed to the Maximally

Likely Landmark Locator (MLLL) and extended with

a subspace-based outlier-correction method called

BILBO in (Beumer et al., 2006).

The maximization of the likelihood ratio is a

heuristic approach, not necessarily leading to the best

position for the landmark. Note that any position

characterized by a likelihood ratio above a pre-set

threshold can be a landmark with certain probabili-

ties of false acceptance and false rejection, dependent

on the threshold. Therefore, we will reformulate the

likelihood-ratio based methods in (Bazen et al., 2003)

and (Beumer et al., 2006) to a MAP approach, thus

giving it a solid theoretical foundation, taking the a-

priori probability of a landmark location into account.

This will prove to make the method robust against

outliers. In a ﬁrst attempt to validate this approach we

performed a simple experiment. Its results show that

the new method performs signiﬁcantly better than the

likelihood-ratio based methods, in particular on low

quality images.

2 THEORY

The shape

s of a face is deﬁned as the collection of

landmark coordinates, arranged into a column vector.

The landmark coordinates belong to a facial area with

texture ~x, measured in a certain region of interest and

also arranged into a column vector. The MAP esti-

mate,

∗

, given a certain texture ~x, can be written as

∗

= argmax

s|~x) (1)

According to Bayes rule, Equation 1 can be written as

∗

= argmax

p(~x|

p(~x)

s), (2)

Beumer G., Veldhuis R. and Boom B. (2009).

MAPPING LANDMARKS ON TO THE FACE.

In Proceedings of the International Conference on Bio-inspired Systems and Signal Processing, pages 12-17

DOI: 10.5220/0001431100120017

 SciTePress

where p(~x|

s) is the probability of the texture ~x given a

landmark location; p(~x) is the background probabil-

ity; and q(

s) is the probability of the shape as func-

tion of the location

s. The quotient Equation 2 is the

likelihood-ratio of the texture belonging to shape

over the overall texture probability. The last factor

takes the probability of the shape at location

s into

account. Ideally, one would like to compute

s from

Equation 2, given all probabilities. This, however

would be prohibitively complex. Therefore a number

of simpliﬁcations are introduced.

Let

∈ R

denote the column vector containing

the spatial coordinates of landmark i = 1...l and ~x

∈

the column vector containing the n pixel values

from the texture in a region of interest surrounding the

assumed landmark i. These landmarks are illustrated

in Figure 1.

Figure 1: Left: the landmarks used from the BioID database

-dots- and from the FRGC -circles-. Right: The shape dis-

tributions map showing the 17 landmarks.

We assume that ~x

only depends on

and that ~x

and~x

, i 6= j, are independent. The latter is plausible if

there is no overlap between~x

and~x

. We also assume

that the landmarks locations are mutually indepen-

dent, though we know this assumption to be incorrect.

However, this assumption creates an easer framework

because then q(

s) can be written as

∏

). In later

work this assumption will be dropped. The distri-

bution of the shapes q(

) is determined empirically

through histograms. This results in a two-dimensional

landscape for each landmark representing the proba-

bility distribution. The probability distributions q(

)

for a number of landmarks can be seen in Figure 1.

With these simpliﬁcations Equation 2 can be rewrit-

ten as:

∗

= argmax

∏

i=1

p(~x

)

p(~x

)

) (3)

The quotients in the product are optimized by the

MLLL algorithm by (Beumer et al., 2006).

3 IMPLEMENTATION

Equation 3 can be rewritten as

∗

= argmax

∑

i=1



log(p(~x

)) −

log(p(~x

)) + log(q(

))



(4)

We assume that p(~x

) is Gaussian with mean µ

l,i

and covariance Σ

l,i

and, likewise, that p(~x

) is Gaus-

sian with mean µ

b,i

and covariance Σ

b,i

. Gaussian

mixture models might model the data better, but they

would also be much more complex. Because of the

assumed mutual independence of the landmarks, the

terms in Equation 3 can be maximized independently.

This makes that the estimation of the shape, for all

landmarks i = 1 . . .l, now is simpliﬁed to

∗

= argmax



−

− µ

l,i

)

−1

l,i

− µ

l,i

) +

− µ

b,i

)

−1

b,i

− µ

b,i

) +

log(q(

s))



(5)

for all landmarks i = 1 . . .l.

3.1 Dimensionality Reduction

Because ~x

consists of a large number of statistically

dependent pixels it is possible and useful to perform

a dimensionality reduction. The covariance matri-

ces, Σ

and Σ

, need to be estimated from training

data. Due to their size, direct evaluation of Equa-

tion 5 would be a high computational burden. Due

to the limited number of training samples available

in practice, they would be rank-deﬁcient or, if not,

too inaccurate to obtain a reliable inverse, which is

needed in Equation 5. For example, a typical train-

ing image consists of between 1000 and 5000 pixels

while there are only 3042 (see Section 4) landmark

samples. Therefore, prior to evaluation of Equation 5,

the vector ~x will be projected onto a lower dimen-

sional subspace. This subspace should have several

properties. First of all, its basis should contain the

signiﬁcant modes of variation of the landmark data.

Secondly, it should contain the signiﬁcant modes of

variation of the background data. Finally, it should

contain the difference vector between the landmark

and the background means for good discrimination

between landmark and background data. The modes

of variation are found by principal component analy-

sis (PCA). See Appendix A for details.

Finally, the landmark and background densities

are simultaneously whitened such that the landmark

covariance matrix becomes a diagonal matrix, Λ

and the background covariance matrix becomes an

identity matrix.

MAPPING LANDMARKS ON TO THE FACE

3.2 Feature Extraction

and Classiﬁcation

The entire process of dimensionality reduction and si-

multaneous whitening can be combined into one lin-

ear transformation with a matrix T

∈ R

n×m

, with n

the dimensionality of the training templates and m the

ﬁnal number of features after reduction.

˜µ

l,i

= T

l,i

, ˜µ

b,i

= T

b,i

(6)

l,i

= T

l,i

b,i

= T

b,i

(7)

(

) = T

~x(

) (8)

For the i-th landmark Equation 5 now becomes

∗

= argmax



−

(~y

(

s) − ˜µ

l,i

)

−1

l,i

(~y

(

s) − ˜µ

l,i

)

(~y

(

s) − ˜µ

b,i

)

(~y

(

s) − ˜µ

b,i

)

+log(q(

s))



(9)

The feature vector,~y

(

s), at location

s for the i-th land-

mark is extracted from texture date in the region of

interest, ~x

(

s). The detailed calculation of the feature

reduction transformation T

is given in Appendix A.

Note that although Equation 9 resembles Equation 5,

the result will be different due to the dimensionality

reduction. This form is however computationally far

more efﬁcient then Equation 5.

4 EXPERIMENTS

Two databases were used. The BioID database (Hu-

manScan, ) was used for training the algorithms, i.e.

estimating T

, ˜µ

l,i

, ˜µ

b,i

l,i

and

b,i

. The FRGC

database (Phillips et al., 2005) was used to test the

algorithms.

The BioID consists of 1521 images of 22 per-

sons. The BioID images have 20 labelled landmarks

of which 17 are used: the eye centres, inner and outer

eye corners, inner of outer ends of the eyebrows, both

nostrils, the tip of the nose, both mouth corners and

the centre of both the upper lip and the lower lip.

For each of these 17 landmarks a MAP classiﬁer was

trained. From each image two positive samples were

taken for each landmark, both symmetrical and asym-

metrical. For all symmetrical landmarks a mirrored

version of the landmark has been added. Asymmet-

rical landmarks, such as the eyes, come in pairs. For

all asymmetrical landmarks a mirrored version of the

other has been added. For example a mirrored ver-

sion of the left eye was used as a right eye. For each

landmark this gives 3042 landmark samples.

The background samples are taken randomly and

uniformly from an area around the landmark location.

Around each landmark from each image ten negative

samples were taken. The minimal and maximal dis-

tance from the landmark location to the centre of the

background training image were ﬁxed. The minimal

distance was 0.25 times the size of the training image.

The maximum distance was the width of the image it-

self. This is illustrated in Figure 2.

Figure 2: The rectangle landmark sample is shown as a solid

line. The + denotes the centre of the image. The grey area

shows the possible locations of the centre of the background

samples. Three possible background samples are shown by

dashed lines.

The FRGC 2.0 database consists of a controlled

set of images with high quality and an uncontrolled

set of images with low quality. Both sets will be used

separately in the experiment. In total the FRGC 2.0

database contains 39328 images, roughly one third

are low quality images and two third are high quality

images. The FRGC 2.0 images have ground truth co-

ordinates for the eyes, nose and mouth. A (Viola and

Jones, 2001) classiﬁer from the OpenCV library (In-

tel, ) was used to locate the face in each image. The

algorithm was run on each face correctly found by the

Viola and Jones classiﬁer (38829, 98.7% of all im-

ages). Since the algorithm always produces an esti-

mate, there are 38829 sets of coordinates to evaluate.

There is a difference between the ground truth co-

ordinates in the FRGC 2.0 database and the landmarks

in the BioID training data. Therefore, we converted

the landmarks found to FRGC ground truth. Several

of the coordinates found by the algorithms are aver-

aged into one compound coordinate, which is com-

pared to the ground truth data. In Table 1 an overview

is given.

Table 1: Overview of the compound coordinates.

FRGC Landmarks found and averaged

Eye Both eye corner and the eye centre.

Nose Tip of the nose and both nostrils.

Mouth Upper lip, lower lip and both mouth corners.

In order to evaluate the quality of the methods

used we used the same measure as in (Cristinacce and

BIOSIGNALS 2009 - International Conference on Bio-inspired Systems and Signal Processing

Cootes, 2006):

n∆

ocl

∑

i=1

i,x

+ δ

i,y

(10)

where n is the number of landmarks, ∆

ocl

the inter oc-

ular distance in the ground truth data, δ

i,x

and δ

i,y

the

displacements of the i-th landmark. This number is

calculated for each image and each landmark. From

the error a bias had to be removed. This was to com-

pensate for offsets in the error due to compounding.

The average of the three points on the nose is not the

same as the tip of the nose. Also both databases could

be labelled differently, what in the BioID is consid-

ered the tip of the nose is not necessary what the mak-

ers of the FRGC 2.0 considered to be the tip of the

nose.

Both MAP and MLLL were run individually and

in combination with BILBO (Beumer et al., 2006).

Original versions of MLLL and BILBO were kindly

availed to us by the authors. All results were evalu-

ated and compared to each other.

5 RESULTS

Figure 1 shows an example of a set of found land-

marks. The red dots denote the estimated landmark

locations and the green circles show the ground truth

data. In Table 1 the relation between the 17 estimates

and the 4 ground truth labels is deﬁned. Most land-

marks estimated were rather accurately and a few are

slightly off.

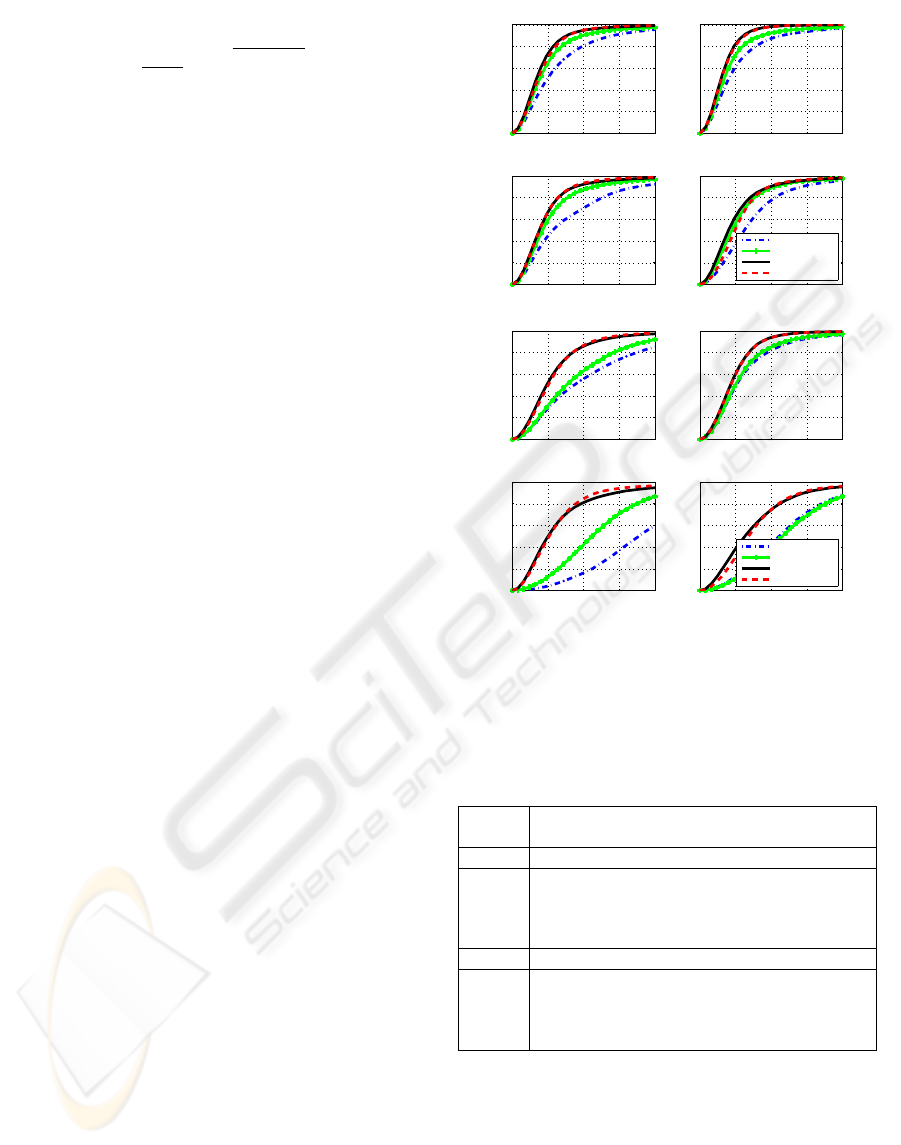
In Figure 3 the cumulative error plots are shown.

They are split into two sets. The top block of 4

plots shows the cumulative errors for the high qual-

ity images and the bottom block of 4 plots for the low

quality images. The upper right plot of each block

of 4 plots shows the overall error. The upper left

plot shows the error for the eyes. The bottom plots

show the graphs for the nose and mouth. In each plot

there are curves for MLLL, MLLL+BILBO, MAP

and MAP+BILBO.

The results are also shown in Table 2. This table

shows the average error for a certain landmark. In or-

der to compare the results, the average errors obtained

by MLLL and BILBO algorithms are also presented.

5.1 Discussion

The MAP method performs better than MLLL on

both the high quality images and the low quality im-

ages. Interestingly, the improvement on the low qual-

ity data is far greater than on the high quality data.

The robustness of the MAP approach is better than

0 5 10 15 20

100

Portion errors

Error in % of the interocular distance

High quality images − All

0 5 10 15 20

100

Portion errors

Error in % of the interocular distance

Eyes

0 5 10 15 20

100

Portion errors

Error in % of the interocular distance

Nose

0 5 10 15 20

100

Portion errors

Error in % of the interocular distance

Mouth

1−MLLL

2−MLLL+BILBO

3−MAP

4−MAP+BILBO

0 5 10 15 20

100

Portion errors

Error in % of the interocular distance

Low quality images − All

0 5 10 15 20

100

Portion errors

Error in % of the interocular distance

Eyes

0 5 10 15 20

100

Portion errors

Error in % of the interocular distance

Nose

0 5 10 15 20

100

Portion errors

Error in % of the interocular distance

Mouth

1−MLLL

2−MLLL+BILBO

3−MAP

4−MAP+BILBO

Figure 3: The cumulative error. Top rows: high quality

images. Bottom rows: low quality images.

Table 2: The average error for the three methods. Total

means the mean RMS error for all coordinates together. The

bracketed number gives the relative improvement of both

MAP and MAP+BILBO compared to MLLL+BILBO.

MLLL MLLL+ MAP MAP+

BILBO BILBO

High quality images

Total 6.8 5.2 4.3 (17%) 4.4 (15%)

Eye 5.7 4.6 3.4 (26%) 3.5 (24%)

Nose 8.2 5.8 4.9 (16%) 4.7 (19%)

Mouth 7.7 5.8 5.4 (7 %) 5.9 (-2%)

Low quality images

Total 11.3 9.6 6.3 (34%) 6.3 (34%)

Eye 6.8 6.5 5.1 (22%) 5.0 (23%)

Nose 18.9 12.6 7.2 (43%) 6.7 (47%)

Mouth 12.6 13.1 8.1 (38%) 8.4 (36%)

that of MLLL. For MAP the gap between the perfor-

mance on the high quality images and the low quality

images is signiﬁcantly reduced compared to MLLL

and MLLL+BILBO. This can be attributed to the a

priori term q(

s). When the likelihood term is rather

ﬂat as a function of

s, the inﬂuence of the q(

s) is

strongest. This seems to occur more often in the low

quality ies than in high quality images.

MAPPING LANDMARKS ON TO THE FACE

Region of intrest

−2

−1

A priori landscape

−30

−20

−10

Likelihood landscape

−100

−80

−60

−40

−20

MAP landscape

−150

−100

−50

Figure 4: The top row shows an eye on the left and on

the right the a priori landscape is presented. The bottom

row presents the likelihood landscape on the left and ﬁnally

the MAP landscape. The blue circles denote the maximum

in that landscape while red dots are the landscape maxima,

shown for easy reference.

In Figure 4 a detailed example for one landmark,

an eye, can be seen. In the upper right corner we see

a region of interest for the eye. The upper right shows

the a priori landscape for this landmark. The lower

left corner shows the likelihood-ratio landscape. This

is the sum of the ﬁrst two terms of Equation 9. Finally,

in the lower right corner the resulting MAP landscape

is shown. In each landscape the location of the max-

imum value is denoted by a large blue circle. In each

of the four images the maxima of the three landscapes

are plotted as a red dot for easy reference. The max-

ima of the likelihood ratio landscape and the MAP

landscape are shown as the two red dots. It can clearly

be seen that because of the inﬂuence of the q(

s) MAP

gives a better estimate of the centre of the eye. It is,

however, also true that the ﬁnal inﬂuence of the q(

term is not always as substantial as in Figure 4. MAP

improves the result here because the likelihood land-

scape is rather uniform in the entire eye region. It

is reasonably save to assume that a part of the im-

provement with regards to MLLL and BILBO can be

attributed to better implementation of the feature ex-

traction then the one in the original MLLL. If a likeli-

hood ratio landscape has a sharp maximum, as in high

quality images, there is not much contribution of the

shape probability to the ﬁnal MAP landscape.

Finally, two interesting observations can be made.

First, applying BILBO is not always beneﬁcial. Ap-

plying BILBO to the MLLL and MAP data makes in-

creases the error for the mouth except for MLLL in

the high quality images. This can be seen in both

Table 2 and Figure 3. Possible explanations for this

effect can be that landmark locations on the mouth

are falsely corrected by BILBO because of grand er-

rors on for instance the nose. Secondly, it is clear that

BILBO does not signiﬁcantly improves MAP while

it does improve the results of the MLLL algorithm.

From this we can conclude that MAP has less severe

outliers and that the limit of BILBO is being reached.

Also, with MAP the shape is already taken into ac-

count more than with MLLL alone. On the other

hand, the fact that using a shape based outlier detec-

tion sometimes still improves the results proves that

there is still room for improvement of the current im-

plementation of the MAP algorithm.

5.1.1 Future Improvements

This method can be further improved by dropping

the assumption made in Section 3 that the landmarks

are independent. This requires a more elaborate op-

timization method for solving Equation 2. Also the

quality of the training data is not sufﬁcient. The

BioID database only contains landmarks from 22 per-

sons. Training on a different database with a bigger

variety of persons might improve the results signiﬁ-

cantly.

Further improvement can be reached by making

an iterative implementation of the algorithm. In the

current implementation, the algorithm trained solely

on registered images. The algorithm responds works

less good on unregistered faces. This has a twofold

negative effect. First the likelihood landscape is cal-

culated for a type of image it has not been trained

to recognize. Secondly the probability distribution of

the shape assumes the head to be aligned. When the

MAP algorithm is used iteratively, an image is better

aligned each run. Thus it has a better ﬁt to the model,

improving the overall accuracy.

6 CONCLUSIONS

We formulated a solid MAP frame work for ﬁnding

the landmarks in a facial image. Our implementation,

however, is only a ﬁrst step towards a complete MAP

landmark location estimator. It shows that using the

MAP probability actually improves the performance

of the MLLL and BILBO algorithms on frontal still

images. MAP has turned out to be more robust be-

cause the performance on the low quality images im-

proved a lot, narrowing the performance gap with the

high quality images. The assumption that we made

that the landmark locations are independent is incor-

rect. The next step will be to introduce the dependen-

cies between the landmarks in order to improve the

estimates of q(

s). Also making an iterative implemen-

tation can improve the MAP approach. Nevertheless

the results are promising.

BIOSIGNALS 2009 - International Conference on Bio-inspired Systems and Signal Processing

REFERENCES

Bazen, A. M., Veldhuis, R. N. J., and Croonen, G. H.

(2003). Likelihood ratio-based detection of facial fea-

tures. In Proc. ProRISC 2003, 14th Annual Workshop

on Circuits, Systems and Signal Processing, pages

323–329, Veldhoven, The Netherlands.

Beumer, G. M., M.Bazen, A., and Veldhuis, R. N. J. (2005).

On the accuracy of eers in face recognition and the

importance of reliable registration. In SPS 2005. IEEE

Benelux/DSP Valley.

Beumer, G. M., Tao, Q., Bazen, A. M., and Veldhuis, R.

N. J. (2006). A landmark paper in face recognition. In

Automatic Face and Gesture Recognition, 2006. FGR

2006. 7th International Conference on, Southampton,

UK, Los Alamitos. IEEE Computer Society Press.

Cristinacce, D. and Cootes, T. F. (2006). Facial feature

detection and tracking with automatic template se-

lection. In FGR ’06: Proceedings of the 7th Inter-

national Conference on Automatic Face and Gesture

Recognition (FGR06), pages 429–434, Washington,

DC, USA. IEEE Computer Society.

Everingham, M. and Zisserman, A. (2006). Regression and

classiﬁcation approaches to eye localization in face

images. In FGR ’06: Proceedings of the 7th Inter-

national Conference on Automatic Face and Gesture

Recognition (FGR06), pages 441–448, Washington,

DC, USA. IEEE Computer Society.

HumanScan. Bioid face db. http://www.humanscan.de/.

Intel. Open computer vision library. http:// source-

forge.net/projects/opencvlibrary/.

Phillips, P. J., Flynn, P. J., Scruggs, T., Bowyer, K. W.,

Chang, J., Hoffman, K., Marques, J., Min, J., and

Worek, W. (2005). Overview of the face recognition

grand challenge. In In Proceedings of IEEE Confer-

ence on Computer Vision and Pattern Recognition.

van Trees, H. (1968). Detection, Estimation and Modula-

tion Theory, Part I. John Wiley and Sons, New York.

Viola, P. A. and Jones, M. J. (2001). Rapid object detection

using a boosted cascade of simple features. In CVPR

(1), pages 511–518.

APPENDIX

A Dimensionality Reduction

The subspace should contain a good representation of

the variations of both the landmark data, X

, and the

background data, X

. Each column of data matrices

and X

is a single training sample x

. Therefore,

two projections matrices U

and U

follow from the

singular value decomposition (SVD)

(l,b)

l,b

= (X

l,b

− M

l,b

), (11)

where M

l,b

= µ

l,b

[1. . . 1], i.e. a matrix whose

columns are the column average of X. For reasons

of computational complexity we only keep the ﬁrst

columns of U

and U

, which represent a ﬁxed amount

of the variance. Here that is 90% of the landmark vari-

ance and 98% of the background variance. The num-

ber of kept columns varies per landmark. So U

and

are not mutually orthogonal and may have possible

overlap

The basis should also contain the difference vector

between both means. Therefore, we add

− µ

|µ

− µ

, (12)

which is the normalised difference between the two

landmark means. Next, we transform [U

] so that

it is orthogonal to u

and obtain

= (I − u

)[U

] (13)

and turn U

into an orthonormal basis of U

= U

(14)

The ﬁnal basis is given by

U = [u

] (15)

Now we reduce the number of features to n by keep-

ing only the ﬁrst n columns of U representing 98% of

the variance.

MAPPING LANDMARKS ON TO THE FACE