THERMOGRAPHIC BODY TEMPERATURE MEASUREMENT

USING A MEAN-SHIFT TRACKER

Guillaume-Alexandre Bilodeau

, Maxime Levesque

, J. M. Pierre Langlois

Pablo Lema

and Lionel Carmant

D´epartement de g´enie informatique et g´enie logiciel,

Ecole Polytechnique de Montr´eal

P.O. Box 6079, Station Centre-ville, Montr´eal (Qu´ebec), H3C 3A7, Canada

Pediatry, Sainte-Justine Hospital, 3175, Cˆote Ste-Catherine, Montr´eal (Qu´ebec), H3T 1C5, Canada

Keywords:

Thermography, Mean-Shift Tracker, Temperature measurement, Epilepsy.

Abstract:

In epilepsy research, using a wide range of sensors can help to automatically detect the occurrence of seizures

and to understand their underlying mechanisms. One such sensor is a thermographic camera that can measure

the surface temperature of the body. This sensor may have an important role in investigating seizures as

studies have shown that they can affect the body temperature of a patient. Furthermore, it has also been

shown that kainic acid, a drug used to provoke seizures in animals, has an impact on rat body temperature.

Consequently, there is a need to continuously measure the evolution of the body temperature of an animal

during seizures. In this paper, we present our developed methodology to measure the temperature of a moving

rat using a thermographic camera. To accurately measure the body temperature, we propose a methodology

using a Mean-Shift tracker. The obtained measures are compared with a ground truth. The method is tested

on a 2-hour video, and it is shown that the Mean-Shift tracker achieves an RMS error of approximately 0.1

◦

1 INTRODUCTION

Neonatal seizures are convulsive events in the ﬁrst

28 days of life in term infants or for premature in-

fants within 44 completed weeks of conceptional age.

Neonatal seizures are the most frequent major man-

ifestation of neonatal neurologic disorders (Volpe,

1989). Population-based studies of neonatal seizures

in North America report rates between 1 and 3.5 per

1000 live births. Most neonatal seizures begin early,

with almost half on the ﬁrst day of life and two-thirds

within the ﬁrst 2 days of life. During the neonatal

period, the brain is most susceptible to the occur-

rence of seizures because of an excess of excitatory

neurons and the inhibitory neurotransmitter GABA

plays an excitatory role. Initially thought to have lit-

tle long-term consequences, we have more and more

evidence that these seizures are deleterious to the de-

veloping brain (Carmant, 2006). Therefore, more

emphasis is put on the treatment of these early life

seizures. However, due to the immature connections

in the neonatal brain, these seizures exhibit unusual

clinical patterns, mimic normal movements and have

primitive EEG patterns that are not easily recogniz-

able. Therefore, one would be required to monitor all

at-risk newborns continuously to conﬁrm the epilep-

tic nature of their events. At Ste-Justine Hospital,

in Montreal, Canada, this typically represents 40 pa-

tients at any one time. For this reason, several au-

thors have addressed automatic detection of neonatal

seizures using video recordings or electroencephalo-

gram (EEG) pattern recognition (Karayiannis et al.,

2001; Karayiannis et al., 2006; Celka and Colditz,

2002; Faul et al., 2005).

Preliminary data from our laboratories on an an-

imal model of neonatal seizures suggest that by us-

ing advanced signal processing, computer vision and

multimodal detection techniques, we can improve the

automatic detection of signiﬁcant clinical events. We

hypothesize that body temperature monitoring may

signiﬁcantly improve the detection and recognition

of neonatal seizures. In fact, it has been shown that

seizures can affect the body temperature of a patient

(Sunderam and Osorio, 2003). It has also been shown

that kainic acid (KA), a drug used to provoke and

study seizures in animals, has a direct impact on the

body temperature of a laboratory rat (Ahlenius et al.,

2002).

Bilodeau G., Levesque M., Langlois J., Lema P. and Carmant L. (2009).

THERMOGRAPHIC BODY TEMPERATURE MEASUREMENT USING A MEAN-SHIFT TRACKER.

In Proceedings of the International Conference on Bio-inspired Systems and Signal Processing, pages 18-24

DOI: 10.5220/0001431300180024

 SciTePress

This paper is part of the ﬁrst phase for testing

our hypothesis with an animal model. It proposes

a method to continuously measure body temperature

using thermography by measuring the temperature of

a signiﬁcant region in each image. Continuous mon-

itoring of body temperature should facilitate the in-

vestigation of its correlation with seizures. In KA-

based studies, it can also help researchers determine

whether the drug has been successfully injected into

the animal.

There are few related works. In a work with

humans (Sunderam and Osorio, 2003), thermal im-

ages of the faces of six patients were acquired ev-

ery hour and during seizure events as indicated by

real-time EEG analysis. Thermal images were ﬁl-

tered manually to removeimages where occlusion oc-

cured. Since the face was in the middle of the image,

the temperature measured is the maximum in the cen-

ter region and there were no tracking requirements.

Other works in avian ﬂu (Camenzind et al., 2006) and

breast cancer (Amalu, 2004) detection using thermog-

raphy have not addressed automated continuous tem-

perature monitoring. In our case, we are interested in

continually monitoring the temperature of a rat that

can move inside a perimeter, so we have to devise a

more automated tracking and measuring method.

The paper is structured as follows. Section 2

presents our measurement methodology. Experimen-

tal results are presented and discussed in section 3.

Section 4 concludes the paper.

2 METHODOLOGY

In this section, we ﬁrst present the acquisition setup

and then we present our measurement methodology.

2.1 Data Acquisition

Our temperature sensor is a Thermovision A40M

thermographic camera (FLIR Systems, Wilsonville,

OR, USA). Before acquiring animal videos, we ﬁrst

assessed the measurement error of the sensor. That

is, we evaluated the measurement precision for a still

object in order to develop a baseline performance ref-

erence. From the manufacturer speciﬁcations, the ac-

curacy is ± 2%. The precision is not speciﬁed. To

evaluate the camera’s precision, we captured thermo-

graphic images of a wood tabletop from a ﬁxed point

of view continuously (at 27 frames/s) for approxi-

mately 30 minutes in a room at about 24

◦

C. The

room temperature was not controlled. We selected

an area of 20 × 20 pixels in the middle of the im-

age. The camera was conﬁgured with a linear mea-

0 200 400 600 800 1000 1200 1400 1600

23.55

23.6

23.65

23.7

23.75

23.8

Seconds

Figure 1: Temperature measured of a tabletop during 1509

seconds, and ﬁtted polynomial to evaluate the measurement

error.

surement range of 20

◦

C to 40

◦

C, and pixels were

quantiﬁed with 8 bits. That is, pixel values of 0 and

255 correspond to temperatures of 20

◦

C and 40

◦

C, re-

spectively. This range provides a reasonable interval

around the expected rat body temperature of approxi-

mately 30

◦

C. The interval between two adjacent pixel

values is 0.078

◦

C. Without averaging a pixel region,

the precision should be one-half of this interval, that

is 0.039

◦

C. By averaging over a region, we may ob-

tain a precision slightly better. The temperature of

the tabletop in each frame is estimated by calculat-

ing the mean of the 10 hottest pixels in the region

of interest. We computed the regression of the data

using a 7

order polynomial and computed the av-

erage ﬁtting error. We used regression because the

temperature of the tabletop is not controlled and we

assume that it changes smoothly. The average pre-

cision is the average ﬁtting error, which is 0.021

◦

with a standard deviation of 0.026

◦

C. Figure 1 shows

the measured temperature and the ﬁtted polynomial.

We did not validate the accuracy as we do not have

the equipment to do so. In our measurements, we are

only interested in the temperature variation, not in its

absolute value. However, in a previous work with the

same camera, the accuracy was evaluated to 0.13

◦

(Camenzind et al., 2006). From the same study, the

drift is said to be negligible.

To acquire thermographic images during animal

experiments, the rat is placed in a metal mesh cubic

cage with an open top (see ﬁgure 2) and the thermo-

graphic camera is angled down toward the cage. The

usual plexiglas cage cannot be used as this material

almost totally reﬂects the heat radiation of the rat and

it is not visible thru it. Furthermore, heat reﬂections

from the rat are also visible on the side walls. Metal

mesh walls do not cause this effect. The camera is

on a 525MV tripod (Manfrotto, Bassano del Grappa

THERMOGRAPHIC BODY TEMPERATURE MEASUREMENT USING A MEAN-SHIFT TRACKER

Figure 2: Camera setup and mesh cage.

(VI), Italy) and pointed toward the open top of the

cage with an angle around 20

◦

with the vertical.

During initial experiments, we quicklydetermined

that the rat fur prevented precise measurements of

the body temperature. Temperature measures on the

whole body are not reliable as they depend on the

thickness of the fur and visible area. We concluded

that the rat should have an area of approximately 10

that is shaved to measure precisely its tempera-

ture. Indeed, the head of the rat, another interesting

region, which is warmer because it has less fur, is not

always visible and it is occluded by a device (Neural-

ynx Cheetah System, Bozeman, MT, USA) to record

local ﬁeld potentials (LFP) signal on the head of the

rat. Observing the rat from the top and shaving a re-

gion on its back give better results, as this region is

almost constantly visible since the rat tends to remain

on its four feet. However, using this strategy means

that we have to use a tracking algorithm to follow the

shaved patch and discriminate it from the head. Fig-

ure 3 shows typical frames that must be processed.

The shaved patch is sometimes severely occluded by

the LFP recording device.

2.2 Measurement Area Tracking

Given the experimental setup and the measurement

strategy, computer vision is needed to track the area

for which we wish to measure temperature. Our work

is based on the following assumptions:

• the images are grayscale, with white (255) mean-

ing hot, and black (0) meaning cold in a given

range;

• the temperature of the rat is higher than its sur-

rounding,particularlyforthe shaved patch and the

head;

• the shaved patch can be occluded by the LFP

(a)

(b)

Figure 3: Two frames of shaved patch to track. (a) With-

out occlusion, (b) with occlusion from the LFP recording

device.

recording device on the head of the rat;

• the rat is always in the camera ﬁeld of view.

Based on these assumptions, we have devised a

tracking method. Ideally, to get automatic measure-

ment for the complete duration of a video, the track-

ing algorithm must not loose track of the patch, and

it must not be distracted by other hot areas like the

head, which may be at a different temperature. For

tracking, we have implemented a Mean-Shift tracker

(Comaniciu et al., 2003).

Our Mean-Shift tracker follows an initially man-

ually selected area. To model the area, we assume

that the temperature inside the patch is mostly similar

for all pixels, and that the area is hotter than the sur-

rounding fur. Hence, a complex kernel and color or

texture modeling is not necessary and, in practice, do

not improve performance. Instead, we use a uniform

kernel and we calculate the probability density func-

tion (pdf) of the pixels with (x,y) coordinates inside

the area A using an histogram with n bins with

Temperature

pd f

(n) = |(x, y)|A(x, y) = n|. (1)

This histogram gives the weight w(x,y) =

Temperature

pd f

(i) of a pixel at coordinates (x,y) in

the area A with a value of i. The weight is equal to

the probability of a given pixel value estimated by the

number of its occurrence. Since most pixels have the

same values, the pixels of the shaved patch have much

BIOSIGNALS 2009 - International Conference on Bio-inspired Systems and Signal Processing

larger weights compared to the surrounding fur. For

each new frame, the histogram is back-projected in

the candidate area, and the Mean-Shift procedure is

applied. After convergence, we estimate the tempera-

ture based on the mean value of the hottest pixels. The

tracking algorithm can be summarized as follows:

1. Initialisation. Manually select the shaved patch

and compute the histogram of the selected area A

of size A

size

For each new frame f :

2. Back-project the histogram in the search area A;

that is replace a pixel value i at position (x,y)

with its number of occurrences in the histogram

(w(x,y) = Temperature

pd f

(i)).

3. Compute the location (x

) of the mean weight

in the search area using the Mean-Shift procedure

with

∑

x× w(x,y)

∑

w(x,y)

(2)

and

∑

y× w(x,y)

∑

w(x,y)

. (3)

4. Center the search area at (x

5. Repeat steps 2, 3 and 4 until convergence. That

is (x

) changes by a value V

less than a given

threshold.

6. Calculate the temperature T

in the search area A

at frame f with

( f) = T

min

+ ((mean(A)/255) ∗ (T

max

− T

min

))

(4)

where T

min

and T

max

are the minimum and maxi-

mum value of the temperature range selected for

the camera.

The tracking algorithm follows an area that in-

cludes more pixels with values that have occurred

very often in the selected region in step 1. Since

the patch is about of constant temperature, the tracker

should follow it continuously. This assumption is val-

idated in the next section.

3 EXPERIMENTATION

In this section, we present the experimentation

methodology, results, and a discussion.

3.1 Experimentation Methodology

To test our measurement method, we have shot a 1h57

video of a Sprague-Dawleyrat(Charles River Labora-

tories, St-Constant, Qu´ebec, Canada) duringan exper-

imentation using 6 mg/kg i.p. of kainic acid (Sigma-

Aldrich Canada Ltd, Oakville, Ontario, Canada). All

experimental procedures conformed to institutional

policies and guidelines (Sainte-Justine Research Cen-

ter, Universit´e de Montr´eal, Qu´ebec, Canada).

The camera setup was described in section 2.1.

The video has 90706 frames at 12.89 frame per sec-

ond with a 320 × 240 resolution and compressed

with Xvid FFDshow encoder (Quality: 100%)

(http://sourceforge.net/projects/ffdshow). The video

was then processed with the Mean-Shift tracking al-

gorithm implemented in Matlab (The MathWorks,

Natick, MA, USA). We used 64 uniformbins (n = 64)

for the histogram. For convergence, we used 0.5 pixel

= 0.5). Temperature calculations were based on

the 10 hottest pixels in the tracked area. T

min

was 20

and T

max

was 40. The size of A was A

size

= 30 (i.e.

30× 30 pixels).

Since we have a large quantity of data, to measure

the performance of our tracking algorithm we used

two metrics. For the ﬁrst metric, we generated a par-

tial ground truth by selecting frames at random over

the whole video sequence. The four corners of the

patch were selected to build a bounding polygon and

the temperature value was calculated as in equation 4.

This gives a set of groundtruth temperatures T

. We

selected F (F = 450) frames. The temperature mea-

surements by the tracking algorithm for these frames

were then compared with the ground truth. The eval-

uation metric is the root mean square error deﬁned as

rms

∑

i=1

(i) − T

(i))

. (5)

The second metric is based on the assumption that

the temperature of the rat’s body changes smoothly.

We computed the regression of the temperatures us-

ing a 23

order polynomial (largest well-conditioned

polynomial). Then, we compute the ﬁtting error. This

gives the average precision µ

and its standard devi-

ation σ

. This ﬁtting error is then compared with the

ﬁtting error obtained for a static target (a tabletop, see

section 2.1) and for the ground truth. If tracking is

good, we expect the average precision (ﬁtting error)

values to be of the same magnitude. That is, we ex-

pect a similar precision in the measurement.

THERMOGRAPHIC BODY TEMPERATURE MEASUREMENT USING A MEAN-SHIFT TRACKER

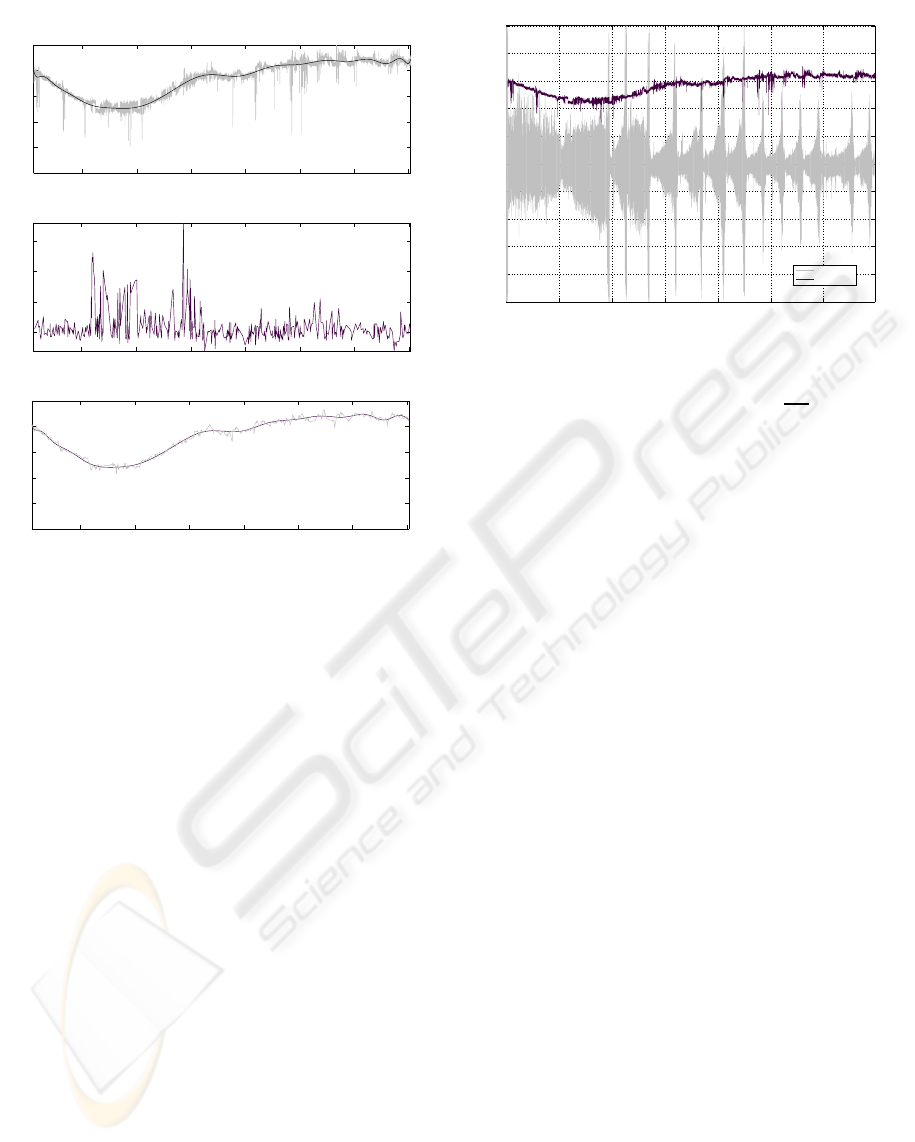
1000 2000 3000 4000 5000 6000 7000

0.2

0.4

0.6

Seconds

1000 2000 3000 4000 5000 6000 7000

Seconds

1000 2000 3000 4000 5000 6000 7000

Seconds

Figure 4: Results from our tracker compared to ground

truth. a) Temperature values obtained with our Mean-Shift

tracker and regression result. b) Errors for the 450 ground

truth points. c) Ground truth temperature values and regres-

sion result.

3.2 Results and Discussion

Figure 4 shows the results obtained for our test video.

The global decrease of the temperature between 0

and about 1800 seconds is caused by the kainic acid.

This phenomenon was previously observed (Ahlenius

et al., 2002) with a rectal thermometer at 15-30 min-

utes intervals. The local changes in temperature ob-

served from 3000 seconds up to the end seem to be

correlated with some seizure events (see ﬁgure 5).

This needs to be investigated further and with more

experiments.

By comparing ﬁgure 4a) and ﬁgure 4c), one can

notice that the tracker result is noisier then the ground

truth. Sudden drops of temperature of more than 1

◦

are caused by tracking errors or occlusions. For ex-

ample, at around 150, 1850, 2100, 4850 and 5100

seconds, the measure is not accurate because of occlu-

sion by the LFP recording device. In such cases, only

a portion of the patch is clearly visible. Sometimes

(e.g., at around 650, 4850 and 5700 seconds), the

tracker is distracted by the rat’s head. The head being

at a different temperature (also depending on its vis-

ibility) it causes a drop in the measured temperature.

1000 2000 3000 4000 5000 6000

−10

−8

−6

−4

−2

time (s)

z−scores (σ) / Temperature (

Intensity

Temperature

Figure 5: Results from our tracker synchonized with LFP

recordings. Temperatures were shifted by -27

◦

C. The LFP

recordings were normalized around a mean µ of 0 and a

standard deviation σ of 1 (Z-scores: z =

x−µ

). Z-scores

larger than ±2σ correspond to seizure events.

Other tracking errors are caused by the frame rate. In

this experiment, the frame rate was only 12.89 frames

per second because the thermographic images were

captured simultaneously with visible images from a

high resolution camera on the same computer. This

low frame rate causes tracking errors when the rat

moves too quickly because it results in a large dis-

placement in the image. In this experiment, it is the

case for the typical wet dog shakes (at about 3800,

4200, 4550, 5350, 6000, 6050 and 6700 seconds)

that follows some seizures. Note that the tempera-

ture measures are not ﬁltered to remove outlier data.

Figure 4b) shows that the errors are mostly positive

with respect to the ground truth. This is because the

tracking errors are caused by erroneously tracking the

head which is slightly warmer than the shaved patch.

Some negative errors are not represented on this graph

since the ground truth is composed of points selected

at random and do not include all the tracking errors.

Table 1 gives the values obtained for the met-

rics deﬁned in section 3.1. First, if we consider the

root mean square error (RMS), our mean-shift tracker

with A

size

= 30 has a value of 0.107

◦

C. This means

that, compared to ground truth, we have an error of

approximately 0.1

◦

C. The impact of this error de-

pends on the temperature changes caused by inter-

esting seizure-related phenomena. If we consider our

tracker with other parameters, using a smaller region

size

= 10) than the shaved patch gives a larger RMS

error. This is because the region is smaller than many

spatial instantaneous position changes of the patch.

Thus, the patch is not in the tracker region of interest

and hence Mean-Shift does not converge to its center.

This results in a measurement area that is often not on

the patch. A

size

should be at least as large as the mo-

BIOSIGNALS 2009 - International Conference on Bio-inspired Systems and Signal Processing

Table 1: Average precision and root mean square error for

each method and for the still object of section 2.1. µ

: av-

erage precision, σ

: standard deviation, T

rms

: root mean

square error.

Method µ

(σ

) (

◦

C) T

rms

(

◦

Still object (section 2.1) 0.021(0.026)

Ground truth 0.079(0.100) 0.000

Mean-Shift A

size

= 10 1.212(1.661) 4.601

Mean-Shift A

size

= 20 0.093(0.159) 0.110

Mean-Shift A

size

= 30 0.090(0.129) 0.107

Mean-Shift A

size

= 40 0.094(0.140) 0.144

tion of the center of the shaved area. If A

size

is selected

too large, the tracker will be distracted very often by

the head of the rat. Thus, the measurement is not reli-

able (A

size

= 40). Recall that the head is not a good re-

gion to track becauseit suffers morefrom LPF record-

ing device occlusion and from occlusions by the rat’s

body. Furthermore, when the tracker jumps from the

patch to the head, there is a measurement error since

they are not at the same temperature.

Table 1 also gives the average precision and stan-

dard deviation based on a regression with a polyno-

mial assuming smooth changes in temperature. Com-

pared to ground truth, our Mean-Shift tracker with

size

= 30 has an average precision about 15% larger

and standard deviation about 30% larger. Precision is

not too far from the ground truth data, but measures

are noisier because of tracking errors. Interestingly,

the ground truth precision is larger than the average

precision obtained for a still object. At this point, we

may hypothesize that it is because the shaved area is

deformable and its normal is not always aligned with

the camera sensor’s normal. Hence, the infrared radi-

ation measured by the camera changes with the angle

of the shaved area. Furthermore, as the shaved area

is deformable, the skin thickness may vary regularly

as it stretches depending on the rat position and atti-

tude. Another possibility is that seizure events cause

temperature changes that violate the smoothness con-

straints and increase the ﬁtting error. We will test a rat

in a control condition (without kainic acid) to verify

the attainable precision with a moving target. Given

these results with our equipment, capture setup, and

assuming smooth temperature change, we can expect

to observe phenomena that cause sudden temperature

changes over a few frames larger than 0.2

◦

Tracking results couldbe improvedtowardground

truth by either improving tracking or by ﬁltering the

temperature values. To improve tracking, the focus

should be to reduce distraction by other warm areas

such as the head. This could be accomplished by ac-

counting for the trajectory of the shaved patch and us-

ing a smoothness constraint. Severe occlusions and

large position changes could be ﬁltered using the pre-

Table 2: Computation times of the Mean-Shift tracker for

the test video sequence (1h57, 90706 frames).

Method Time (s) Frames/s

Mean-Shift A

size

= 10 16100 5.6

Mean-Shift A

size

= 20 15854 5.7

Mean-Shift A

size

= 30 16365 5.5

Mean-Shift A

size

= 40 16087 5.6

vious and following frames over a time window. A

higher frame rate would also reduce the occurrence

of large position changes.

Table 2 shows the computation times required to

process the whole test sequence using MATLAB on

a Opteron 250 2.4 GHz computer (Advanced Mi-

cro Devices, Sunnyvale, CA, USA). We can process

approximately 5.6 frames/s. The processing time is

mostly constant for the tested values of A

size

. This is

because the processing time is related to convergence

of the Mean-Shift procedure (step 5 in section 2.2)

more than to processing a larger number of pixels in

area A.

4 CONCLUSIONS

This paper presented a methodology to measure the

body temperature of a moving animal in a laboratory

setting. Because of the experimental setup, uneven

thickness of the fur with viewpoint and the possibil-

ity of occlusion, we have concluded that we needed

to shave a region on the back of the rat. Since the

head and this shaved region can have different tem-

peratures, tracking is required to measure temperature

on the same body region continuously. We proposed

a Mean-Shift tracker based on the probability density

function of the temperature of a manually selected

area.

Our method was tested on a 2-hour video se-

quence with a rat having seizures at regular intervals.

Results show that our tracker achieves measurements

with an RMS error of 0.1

◦

C. Errors are caused by se-

vere occlusions or by distracting warm regions such

as the head. Although we estimate we can observe

phenomena causing changes of more than 0.2

◦

C, we

do not obtain a precision similar to a still object. Part

of this difference with camera precision is caused by

the tracker, while another part is caused by other rea-

sons. We hypothesize that changes in the orientation

of the measured surface cause measurement errors, so

it may not be possible to attain the precision obtained

on a still object. Furthermore, in the test video, tem-

perature changes may not be smooth and they may

increase the ﬁtting error by a polynomial.

THERMOGRAPHIC BODY TEMPERATURE MEASUREMENT USING A MEAN-SHIFT TRACKER

Future works include the improvement of the

tracking algorithm by adding trajectory smoothness

constraints. That is, the change in position in the im-

age of the tracked area should be smooth. Further-

more, ﬁltering will be applied to the temperature mea-

sures to remove outliers. We will also investigate the

impact of changes of orientation of the measured sur-

face. Finally, we want to apply this methodology in

more experiments and automatically detect abnormal

events based on changes in the body temperature.

ACKNOWLEDGEMENTS

We would like to thank the Canada Foundation for

Innovation (CFI) for their support (grant 10420).

REFERENCES

Ahlenius, S., Oprica, M., Eriksson, C., Winblad, B., and

Schultzberg, M. (July 2002). Effects of kainic acid

on rat body temperature: unmasking by dizocilpine.

Neuropharmacology, 43(1):28–35.

Amalu, W. (2004). Nondestructive testing of the hu-

man breast: the validity of dynamic stress testing in

medical infrared breast imaging. In Engineering in

Medicine and Biology Society, 2004. IEMBS ’04. 26th

Annual International Conference of the IEEE, vol-

ume 2, pages 1174–1177.

Camenzind, M., Weder, M., Rossi, R., and Kowtsch, C.

(2006). Remote sensing infrared thermography for

mass-screening at airports and public events: Study to

evaluate the mobile use of infrared cameras to identify

persons with elevated body temperature and their use

for mass screening. Technical Report 204991, EMPA

Materials Science and Technology.

Carmant, L. (2006). Mechanisms that might underlie pro-

gression of the epilepsies and how to potentially alter

them. Advances in neurology, 97:305–314.

Celka, P. and Colditz, P. (May 2002). A computer-aided de-

tection of eeg seizures in infants: a singular-spectrum

approach and performance comparison. Biomedical

Engineering, IEEE Transactions on, 49(5):455–462.

Comaniciu, D., Ramesh, V., and Meer, P. (May 2003).

Kernel-based object tracking. Pattern Analysis

and Machine Intelligence, IEEE Transactions on,

25(5):564–577.

Faul, S., Boylan, G., Connolly, S., Marnane, L., and Light-

body, G. (July 2005). An evaluation of automated

neonatal seizure detection methods. Clinical Neuro-

physiology, (7):1533–1541.

Karayiannis, N., Srinivasan, S., Bhattacharya, R., Wise,

M., Frost, J.D., J., and Mizrahi, E. (Sep 2001). Ex-

traction of motion strength and motor activity signals

from video recordings of neonatal seizures. Medical

Imaging, IEEE Transactions on, 20(9):965–980.

Karayiannis, N., Tao, G., Frost, J.D., J., Wise, M.,

and Mizrahi, E. (July 2006). Automated detec-

tion of videotaped neonatal seizures based on mo-

tion segmentation methods. Clinical Neurophysiol-

ogy, (7):1585–1594.

Sunderam, S. and Osorio, I. (August 2003). Mesial tempo-

ral lobe seizures may activate thermoregulatory mech-

anisms in humans: an infrared study of facial temper-

ature. Epilepsy and Behavior, 49(4):399–406.

Volpe, J. J. (1989). Neonatal Seizures: Current Concepts

and Revised Classiﬁcation. Pediatrics, 84(3):422–

428.

BIOSIGNALS 2009 - International Conference on Bio-inspired Systems and Signal Processing