
PREDICTING THE OUTCOME OF TUBERCULOSIS
TREATMENT COURSE IN FRAME OF DOTS
From Demographic Data to Logistic Regression Model
Sharareh R. Niakan Kalhori and Xiao-Jun Zeng
School of Computer Science, Oxford Road, University of Manchester, Manchester, M13 9PL, U.K.
Keywords: Predicting, Tuberculosis, DOTS, Demographic Data, Logistic Regression.
Abstract: About fifteen years after the start of WHO’s DOTS strategy, tuberculosis remains a major global health
threat. Patients vary considerably in their performance in completing treatment course of tuberculosis.
Defect in treatment completion have serious undesirable consequences. Although several studies have
predicted outcome of treatment for pulmonary tuberculosis, few tools are available to identify high risk
patients in finishing treatment course and getting cure prospectively. A logistic regression model proposed
to predict the given outcome applying patient demographic characteristics related to just less than 10,000
tuberculosis patients diagnosed by Iranian health surveillance system in 2005. Several tests validate the
developed model, X
2
(6) = 351.902, P < 0.0001. Also, the model confirmed the significant role of
considered factors, calculating the odds ratio of outcome occurring based on each category of variables and
explaining the possibility of using the model in other similar patient population. In brief, to support the
decision of how intensive the carrying out of DOTS should be for each patient, the predictive models like
logistic regression could be useful.
1 INTRODUCTION
Tuberculosis (TB) caused by Mycobacterium
tuberculosis, still is a serious world’s public health
problem, particularly in middle-and low-income
countries, known as the ninth leading cause of death
and disability in the whole world (Obermeyer et al.,
2008). The control of TB is mainly based on early
detection and complete treatment of active cases,
reducing transmission by control and prevention
strategies. Since 1993, Directly-observed treatment,
short-course strategy (DOTS) has been an
international approach to control of tuberculosis
(TB), aimed to prevent the transmission of M.
tuberculosis by emphasizing on passive case
detection and standardized, directly observed
treatment of sputum smear positive cases. In spite of
the impressive progress in DOTS implementing,
there is an estimation of around 9 million people
developed TB for the first time and 1.7 million
people died with or from the disease globally
(Harries & Dye, 2006). Although about one-third of
the world’s population is infected with M.
tuberculosis, patients who have not received
completed treatment course transmit the disease
actively enhanced by other risk factors like
HIV/AIDS pandemy. In fact, uncompleted treatment
course and not entirely cured cases, not only do not
remove themselves from the prevalent pool but are
going to add more infected cases. Moreover,
multidrug-resistance TB (MDR-TB) and HIV-
associated TB can be accounted as problems resulted
from failure of TB control properly (Juzar, 2005).
Hence, the World Health Organization put the
Standardized treatment with supervision and patient
support which is one of the DOTS elements (WHO,
2006).
Some studies focused on developing models to
predict tuberculosis control situation under the
WHO`s DOTS strategy either globally or regionally
in an epidemiological approach. Dye et al. (1998)
explored the characteristics of tuberculosis control
under DOTS and predict the effect of improved case
finding and cure on tuberculosis epidemics for each
of the six WHO regions through developing an age-
structured mathematical model. The result of this
study showed that during the years from 1998 to
2020 the annual incidence of TB is expected to grow
by 41%, minimum 7.4 million per year even though
129
R. Niakan Kalhori S. and Zeng X. (2009).
PREDICTING THE OUTCOME OF TUBERCULOSIS TREATMENT COURSE IN FRAME OF DOTS - From Demographic Data to Logistic Regression
Model.
In Proceedings of the International Conference on Health Informatics, pages 129-134
DOI: 10.5220/0001431401290134
Copyright
c
SciTePress

WHO`s efforts prevent 23% or 48 million cases by
2020. This study applied time as a parameter to
develop the model and it was only able to forecast
the condition of TB control based on the affected or
dead population for different age groups and not for
discrete sex. Another study developed an
epidemiological model to predict the number of TB
related cases and deaths for five regions of the world
between 1998 and 2030 (Murray & Salomon, 1998).
In contrast of these two population based studies,
there are some investigations to predict the outcome
of TB through focusing on the patients status. One
of these studies which just considered pulmonary
tuberculosis was aimed to develop a multivariate
model predicting the response to therapy
prospectively. The subject of study was restricted to
42 non HIV infected cases with drug resistance TB.
The source of data was a prospective study
conducted in Uganda and Brazil. To predict the
duration of positive culture for considered patients,
multiple linear regression analysis was carried out
(Wallis et al., 2000).
In order to developing a correct model, counting
the correct predicting factors is very crucial.
Predictive factors for non-completion of tuberculosis
treatment course have been investigated in a study
among 2201 HIV-infected TB patients in Barcelona
during the years 1987- 1996. The investigators
compared patients who finished treatment course
properly to those who gave up using
2
x test in a
bivariate analysis. The main criterion to measure the
associations was odd ratios (OR) with 95%
confidence internal (CI) revealing these results that
intravenous drug using (IDU), area of residency and
the level of socio-economic status, homelessness,
history of TB, and having presented with a current
TB episode during the years of study were known as
risk factors for quitting the course treatment
(Tanguis et al., 2000). HIV positive patients and
those who don’t obey all treatment rules and
regulations have been reported as high risk cases for
recurrence of tuberculosis (Picon et al., 2007).These
studies showed the factors which are influential on
the given outcome; however, predicting models to
determine patients’ success treatment course
completion and getting cured in more detail using
the patients characteristics have been lacking.
Besides, the purpose of present study was to develop
and validate a logistic regression model to verify
predictors of tuberculosis treatment completion
outcome, how the relationship of them were with
considered outcome with 95% CI, and calculating
the probability of successes in completing the course
of treatment and getting cure. This statistical model
can then be used in making decision about how
intensive should be the DOTS following up
activities for TB affected patients. Hence, this study
aims to exploit available knowledge of risk factors
for occurrence of TB to develop a model predicting
the treatment success in patients who have applied
DOTS.
2 SUBJECTS AND METHODS
2.1 Data
A retrospective analysis was performed in 9886
subjects who were involved in the process of DOTS
from registration stage to diagnosis and treatment of
TB. In fact, the derivation data set was composed of
all reported cases in Iran from whole country in
2005. Novel professional software, ‘Stop TB’, third
edition, version 2.1.3.102 particularly developed for
data collection of TB treatment process based on
DOTS in 2003 was used. Demographical data as
independent variables including Age, Sex, Weight,
Area of residency, History of prison, and Nationality
were applied. Also, for each patient dependent
variable was recorded whether or not the patient
finished the treatment course and get cured.
2.2 Logistic Regression Model
To quantify the association of each independent
variable with outcome, a logistic regression model
was developed. In this model, probability of
completed treatment course and cure was function of
each independent variable as mentioned above.
Initially, since several epidemiological case-control
studies addressed demographical characteristics as
influential factors effecting on tuberculosis
incidence rate (Davidow et al., 2003; Buskin et al.,
1994), they were applied to develop a predicting
binary logistic regression model.
The binary logistic regression equation is as
follows when there is:
inn
XbXbXbb
e
YP
ε
+++++−
+
=
....(
22110
1
1
)(
(1)
In which P(Y) is the probability of Y occurring,
series of predictor variables (X
1,
X
2,
…,Xn)
,
to predict
the probability of Y, e is the base of natural
logarithms, b
0
which is a Constance, a predictor
variable (X
1
), and a coefficient for every predictor
like b
1,
or b
n
(Field, 2005). To develop the model, the
HEALTHINF 2009 - International Conference on Health Informatics
130

Statistical Package for the Social Sciences (SPSS for
windows, release 15) was applied. Regression
analysis can occasionally be improperly affected by
variables that are not normally distributed, or by a
small number of outlying observations; thus, several
tests were performed to examine these concerns.
Having analysed the prepared data in SPSS, the
estimated coefficients and their associated standard
errors were calculated in addition to the covariance
and 95% Confidence Interval (CI) around the
estimated probabilities of considered outcome for
each case. Data entered in Forward Stepwise
fashion. In order to assess the model, the log-
likelihood statistics, Hosmer & Lemeshow`s R
2
L
,
Cox& Snell `s R
2
CS,
and Nagelkarke R Square were
calculated. Also, to check the fitness of model and
the contribution of predictors Hosmer &
Lemeshow`s goodness-of-fit and Wald statistics test
were tested. Value of EXP (β) was an indicator of
the validity of model, similar to the b-coefficient,
expressing the odds of occurring the concerned
outcome and the utility of model in other similar
patient population with 95% Confidence Interval
(95.0% C.I. for EXP (β)). Furthermore, in order to
multicollinearity diagnosis, the tolerance and VIF
were checked.
3 RESULTS
According to obtained result, the overall fit of the
model was significant for all entered variables.
-2LogLikelihood decreased from 10892 in block 0 to
10541 at the last step of the first block. In fact, this
change of 351 was the amount of the model’s chi-
square, X
2
(6) = 351.902, P < 0.0001.
The classification test showed that 90% of cases
could be correctly classified using these predictors.
Hosmer & Lemeshow`s goodness-of-fit statistic test
checked the hypothesis that the observed data were
significantly different from the predicted value from
the model. Non-significant value for Hosmer and
Lemeshow`s goodness-of-fit test refused the
hypothesis that the observed data were significantly
different from the predicted values from the model.
Therefore, no significant result, the X
2
(8) =14,
P=0.065 indicated that the model did not differ
significantly from the observed data, predicting the
real world data fairly well. The significant value of
the Wald statistics for each predictor demonstrated
that all considered parameters were able to predict
the outcome of TB treatment significantly, (P<0.007)
and applied variables contributed significantly to the
predictive ability of the model.
As shown in table 1, B values are the values
which should be used in equation 1 to calculate the
probability of a case falling into a specific category.
The confidence interval for EXP (ß) associated to all
6 targeted parameters didn’t not cross 1, giving this
confidence that the relationship between each of
them and outcome of interest revealed in this sample
would be found in 95% of samples from the same
population.
The value of Exp (ß) for age was less than 1,
which means that if age increases by one year, then
the odds ratio of positive outcome decrease (Exp
ß=0.988, CI
0.96
= 0.986 to 0.991). That is, getting
older has negative effect on patient success to end
the course of treatment and get cure.
Also, the value of Exp ß for nationality was less
than 1 (Exp ß=0.988, CI
0.95
= 0.986 to 0.991) which
revealed the negative relationship between this
variable and considered outcome. In other words,
when the nationality changes from Iranian to
Afghani, Pakistani, and Iraqi, the odds of successful
completion of tuberculosis treatment course is more
decreased respectively. In brief, as nationality
changes from Iranian to Afghani, Pakistani, or Iraqi
subjects are about 0.98% times less likely to have
successful completion of their Tuberculosis
treatment.
Another predictor with Exp ß less than 1 and
negative relationship was the recent stay in prison
(Exp ß= 0.815, CI
0.95
= 0.721 to 0.921). This result
reveals that if the prison residency increases by one
point, then the odds of given outcome decreases. It
means that being in prison decreases the probability
of completed treatment course; prison can be
considered as a risk factor to fail completing
treatment course and cure the disease 0.815 times
more than others.
Gender (Exp ß= 0.455, CI
0.95
= 0.408 to 0.507)
showed that if it changes from male to female, the
odds of positive outcome decreased and females
0.455 time less likely to have completed treatment
course and cure rather than males.
Exp ß for Weight and Area were a little greater
than 1, 1.023 and 1.174 respectively. It shows that
they have a slight effect on the odds of the
considered outcome.
PREDICTING THE OUTCOME OF TUBERCULOSIS TREATMENT COURSE IN FRAME OF DOTS - From
Demographic Data to Logistic Regression Model
131
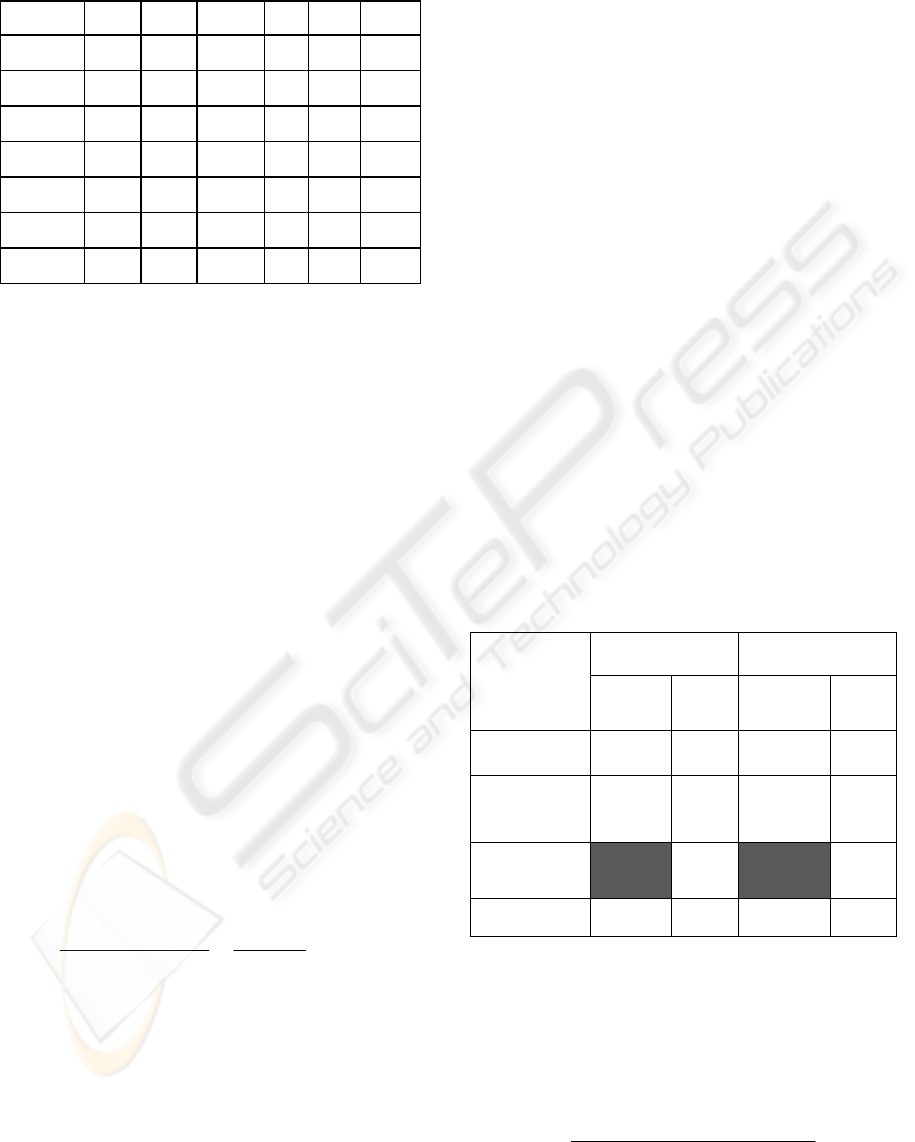
Table 1: Patient demographic characteristics as variables
in the equation.
B S.E. Wald df Sig. Exp ß
Constant 2.1 .159 179 1 .000 8.433
Age -.01 .001 88 1 .000 .988
Weight .02 .002 111 1 .000 1.023
N
ationality .02 7.3 1 .007 .948
Area .16 .05 9.2 1 .002 1.174
Prison -.2 .06 10.7 1 .001 .815
Gender -.7 .05 200 1 .000 .455
The result of the analysis to reveal multicollinearity
addressed that there was not any collinearity among
the variables. According to the Menard suggestion in
1995, the cut-off point for tolerance value is 0.1 and
VIF value greater than 10 is cause for concern (Field,
2005). The tolerance values for all variables were
close to 1; all the value of VIF criterion were less
than 10. In company with Collinearity Diagnosis
output, there were Eigenvalues of the scaled, the
condition index and the variance proportions for
each predictor. If each of the Eigenvalues is much
larger than others, then the uncentred cross-products
matrix is said to be ill-conditioned, which mean the
solutions of the regression parameters can be greatly
affected by small changes in the predictors or
outcome. Here, the final dimension had a condition
index of 22.418 which wasn’t really different from
the other dimensions verifying there wasn’t any
collinearity among the considered variables. Having
looked at the variance proportion, it was clear that
there wasn’t any dependency of variances of their
regression coefficients because of the lack of
predictors that have high proportions on the same
small Eigenvalues.
The measure of Hosmer and Lemeshow`s R
2
calculated as following equation:
967.0
9.10892
9.10541
)(2
)(2
2
==
−
−
OriginalLL
ModelLL
R
L
(2)
This criterion can vary between 0 and 1 expressing
that the predictors are useless or perfect at predicting
the outcome respectively. In this case, the model
could predict the outcome well since its value was
almost 1.
3.1 Validation
Train and Test is the most common approach to
assess a predictive model pursuing the goals of
reducing model over-fit, providing a realistic
estimate of model accuracy and improving
generalization when the model is used on new data .
This method is composed of building a predictive
model with training sample and then validates the
model using an independent test sample. Therefore,
whole data set was divided in three parts, using 70%
of them for training and 30% as testing sample. As
shown in table 2, chi square for both training and
testing model both are significant , 222.3 and 123.4
respectively when p<0.000, df=6 are same for both.
The amount of Standard Error for both training and
test models became less from original to final model.
Furthermore, the value of
2
R
calculated through
dividing the chi-square by the original -2 log
likelihood states either training or test models can
account for more than 40% of the variance of
desirable outcome for treatment course of
tuberculosis and about 60% of what makes an
completed treatment course and cure for a patient is
still unknown. This model can correctly classify
most cases, just under 90%.
Table 2: Comparative results of training and testing data to
show the model’s validation.
Training Data Testing Data
Original
Model
Final
Model
Original
Model
Final
Model
-2Log
likelihood
6096.9 5874.6 2672.9 2549.5
SE
(Standard
Error)
0.033 0.257 0.049 0.421
Correlation
Coefficient
(R
2
)
0.41
0.45
Classification
Rate
82.2 90.5 82.1 89.8
Moreover, data of testing data were applied for
training model and the significant percent of
probability of outcome of successful completion for
treatment or getting cure were forecast for patients,
sing information of table 1 and equation 1 as follows:
P (completion treatment course or getting cures)
)....(
22110
1
1
ε
+++++−
+
=
nn
XbXbXbb
e
HEALTHINF 2009 - International Conference on Health Informatics
132

Hence, for a female, 79 year old patient with 33 kg
weight and Iranian nationality , living in rural area
with no history of being recently in prison, using the
value of
0
b =1.58,
age
b =-0.012,
gender
b = 0.807,
ynationalit
b = -.039,
prision
b = -0.263,
area
b =0.15,
weight
b =0.021 we will have
Y=
)15.003.026.07.094.061.158.1(
1
1
+−−+−+−
+ e
= 80%
Therefore, there is 80% chance that she will have a
completed course for TB treatment or be cured
entirely.
4 DISCUSSIONS
Pursue high-quality DOTS expansion and
enhancement is one of the most crucial components
of revised Stop TB strategy, as developed by the
World Health Organization in 2006, for reaching the
Millennium Development Goals to control of
tuberculosis by 2015 (WHO, 2006).It has several
prominent features as an internationally well known
approach to control of TB, implemented in 182
countries by 2003. However, Degree of DOTS
success varies in deferent situations and regions. For
instance, in 2002, despite high level of overall
frequency of treatment success under DOTS, close
to the 85%, it has been reported that 20% of TB
patient were lost to follow-up and over the same
period in Europe, 6% of patients failed treatment by
the time of relatively common of drug resistance
cases (Obermeyer et al., 2008). Although these
mentioned failures may be attributed to different
reasons, DOTS is relatively passive services and all
patients` following up is difficult in practice. Fully
implementing this strategy, on the other hand, is not
cheap process. Based on the conducted studies, It
has been estimated that to carry out DOTS strategy
practically in 22 high–burden country which
accommodated approximately 80% of the world’s
TB patients, $1 billion annually is needed during the
years 2001-2005, as well as $ 0.2 billion for other
left countries in the same time per year. Thus, about
$ 300 million per year is accounted as a resource gap
(Floyd et al., 2002). Deliberation and assessment of
the output of present study ensured that all targeted
demographic data have significant role to predict the
outcome of tuberculosis treatment P<0.05 and can
be applied to a patient specific consultation as one
type of decision support functions. In other words,
using this model make the opportunity to find the
patient with high risk of fail in completing treatment
course in DOTS and determining how much
intensive care is required for each patient. Even
though numerous studies in developing model with
predictive ability exist (Abu-Hanna& Lucas, 2001),
this model is simply using the demographic
parameters which can be accessible in many health
care systems. However, in the area of prediction,
particularly in medicine, the logistic regression
method is typically used to estimate the probability
of a dichotomous outcome of interest. Because of
this limitation, more sophisticated modelling
techniques with ability of predicting other type of
given outcome are required.
ACKNOWLEDGEMENTS
We are grateful to Iranian Ministry of Health and
Medical Education for funding; department of
tuberculosis and Leprosy control for data Access,
helps and advice.
REFERENCES
Abu-Hanna, A., Lucas, P.J.F., 2001. Prognostic Models in
Medicine, AI and Statistical Approaches. Methods of
Information in Medicine, 40 ,1-5.
Buskin, S.E., Gale, J.L., Weiss, N.S., Nolan, C.M., 1994.
Tuberculosis Risk Factors in Adults in King County,
Washington, 1988 through 1990. American Journal of
Public Health, 84(11), 1750-1756.
Davidow, A.L., Mangura, B.T., Napolitano, E.C.,
Reichman, L.B., 2003. Rethinking the
Socioeconomics and Geography of Tuberculosis
among Foreign-born Residents of New Jersey, 1994-
1999. American Journal of Public Health, 93(6), 1007-
1012.
Dye,C., Garnett G.p., Sleeman K., Williams B.G., 1998.
Prospects for Worldwide Tuberculosis Control under
the WHO DOTS Strategy. The Lancet, 352(12), 1886-
1891.
Field A., 2005. Discovering Statistics Using SPSS. SAGE
Publication LTD, London, 2
nd
edition.
Floyd, K., Blanc, L., Raviglione, M., Lee, J. 2002.
Resource Required for Global Tuberculosis Control.
Science, 295, 2040- 2041.
Harries, A.D., Dye, C., 2006. Tuberculosis. Annals of
Tropical Medicine & Parasitology, 100(5, 6), 415-30.
Juzar, A., 2005. The Many Faces of Tuberculosis Control
and the Challenges Faced. Business Briefing: US
Respiratory Care, 1-4.
Murray C. J. L., Salmon J.A. 1998. Modelling the Impact
of Global Tuberculosis Control Strategies.
Proceedings of the National Academy of Sciences of
PREDICTING THE OUTCOME OF TUBERCULOSIS TREATMENT COURSE IN FRAME OF DOTS - From
Demographic Data to Logistic Regression Model
133

the United States of America, 95(11)13881-13886.
Obermeyer, Z., Abbott-Klafter, J., Murray, C.J.L., 2008.
Has the DOTS Strategy Improved Case Finding or
Treatment Success? An Empirical Assessment. PloS
ONE, 3 (3), e1721.
Picon, P.D., Bassanesi, S. L., Caramori, M. L. A., Ferriera,
R. L. T., Jarczewski, C. A., Vieira, P. R. B., 2007.
Risk factors for recurrence of tuberculosis. J. Bras
Pneumol, 33(5): 72-578.
Tanguis, H.G., Cayla, J. A., Garcia de Olalla, P., Jansa
J.M., Brugal, M.T., 2000. Factors predicting non-
completion of tuberculosis treatment among HIV-
infected patients in Barcelona (1987-1996).
International Journal of Tuberculosis and Lung
Disease, 4(1), 55-60.
Wallis R.S., Perkins M.D., Phillips M., Joloba M.,
Namale A., Johnson J.L., Whalen C.C., Teixeira L.,
Demchuk B., Dietze R., Mugerwa R.D., Eisenach K.,
Ellner J.J., 2000. Predicting the Outcome of Therapy
for Pulmonary Tuberculosis. American Journal of
Respiratory and Critical Care Medicine, 161, 1076-
1080.
World Health Organization, 2006. The Stop TB Strategy,
Document WHO/HTM/TB/2006.35. Geneva: WHO.
HEALTHINF 2009 - International Conference on Health Informatics
134
