MODELING OF MERIDIAN CHANNELS

imin Wang

1,2

, Yonghong Tan

2∗

School of Electronic Engineering, Xidian University, Xi’an, 710071, China

Miyong Su

College of Mechanical and Electronic Engineering, Shanghai Normal University, Shanghai, 201814, China

Keywords:

System identiﬁcation, Modeling, Meridian systems, Acupuncture points.

Abstract:

In this paper, the auto-regressive and moving average (ARMA) models are constructed for the meridian chan-

nels based on the measuring data obtained from the acupoints in the Lung Channel of Hand-Taiyin (LU),

the Pericardium Channel of Hand-Jueyin (PC). For comparison, the ARMA models for the contrastive non-

acupoints around the measured acupoints are also obtained. Then, the analysis based on the zeros-poles

distribution of the obtained models is implemented.

1 INTRODUCTION

With the development of the research in the tradi-

tional Chinese medicine, many research reports had

shown great interest in the acupuncture-therapy. It

has been found that the acupuncture points (for ab-

breviation, we call them as acupoints) are distributed

in the meridian system of the human body. Moreover,

meridian system is an independent system which ex-

ists in parallel with neural systems and blood circu-

lation systems. The acupuncture points distributed

in the meridian system possesses many distinctive

ways for transferring signals and processing infor-

mation including electrical information (J. Julia and

FACOG, 1998). Moreover, the experimental results

have shown that the meridian system is an optimum

path for transferring information and works with a

close relation to the cerebral cortex and whole neu-

ral systems.

So far, the investigations on the meridian system

for acupuncture points are mainly concentrated on

the measurement of the resistance and potential, ca-

pacitance and conductivity distribution between acu-

points (F. III John and Erlichman, 2005; Yang, 1997;

W.Zhang and Zhu, 1999). However the research

on the features as the electrical signal transmission

through the meridian system with acupuncture points

has seldom been involved. Motivated by the phe-

nomenon that the meridian system is an optimum path

for transferring information, in this paper, we use a

sequence of pseudo-random signal to stimulate the

Lung Channel of the Hand-Taiyin (LU) and the Peri-

cardium Channel of the Hand-Jueyin (PC). Then the

corresponding responses of the acupoints on those

channels are measured. Based on the obtained data,

the corresponding ARMA models are constructed by

using least squares algorithm. Those derived ARMA

models can be used to analysis the static and dynamic

characteristics of the meridian channels.

The paper is organized as follows. Section II

describes the experimental conﬁguration for electric

stimulation and measurement of the corresponding re-

sponses of the acupoints and non-acupoints. Then the

AMRA models obtained based on measured data are

illustrated in Section III. In Section IV, the conclusion

will be given.

2 EXPERIMENTAL

CONFIGURATION

In this paper, a method based on three detecting elec-

trodes is used to measure the stimulation and the

corresponding response of the acupuncture points on

meridian systems. The architecture of the measure-

ment for meridian signal is shown in ﬁgure 1. The

167

Wang Z., Tan Y. and Su M. (2009).

MODELING OF MERIDIAN CHANNELS.

In Proceedings of the International Conference on Biomedical Electronics and Devices, pages 167-172

DOI: 10.5220/0001433001670172

 SciTePress

three-electrode method of detecting the acupoint sig-

nal has the advantage of good operability and high

signal accuracy. The signal captured was affected by

skin moisture and electrode contact pressure. In order

to reduce the impact of test environment, we keep the

same test condition on every volunteer.

Figure 1: Acupoint signal measuring method using three-

electrodes.

The stimulation signal was a sequence of pseudo-

random current signal produced by a computer. This

signal is shown in ﬁgure 2.

Figure 2: The stimulation signal fed to acupoints.

In this experiment, the pseudo-random currents

through two electrodes stimulate acupoint 1 and acu-

point n of the measured meridian. Then detecting

electrode was used to measure the response of acu-

point m located in between acupoint 1 and acupoint

n. The outputs of the measured acupoints were trans-

ferred through a current/voltage conversion circuit

then sampled by an analog / digital convertor. The

sampled signals were sent to the computer for fur-

ther processing. There were 20 healthy volunteers ac-

cepted the test. Before the test, the volunteers were

relaxed to avoid the strenuous disturbance. Based on

the theory of Chinese medicine, there are 11 acupoints

in the Lung Channel of Hand-Taiyin. In this experi-

ment, the stimulating acupoints are Tianfu (LU 3) and

Taiyuan (LU 9) which is considered as the ground, the

detecting acupoints are Xiabai(LU 4), Chize (LU 5),

Kongzui (LU 6), Lieque (LU 7) and Jinqu (LU 8) re-

spectively. The Pericardium Channel of Hand-Jueyin

includes a total of 9 acupoints. In the experiment,

Tianquan (PC 2) and Laogong (PC 8) are respectively

the stimulating point and ground. The detecting acu-

points are respectively Quze (PC 3), Ximen (PC 4),

Jianshi (PC 5), Neiguan (PC 6), and Daling (PC 7).

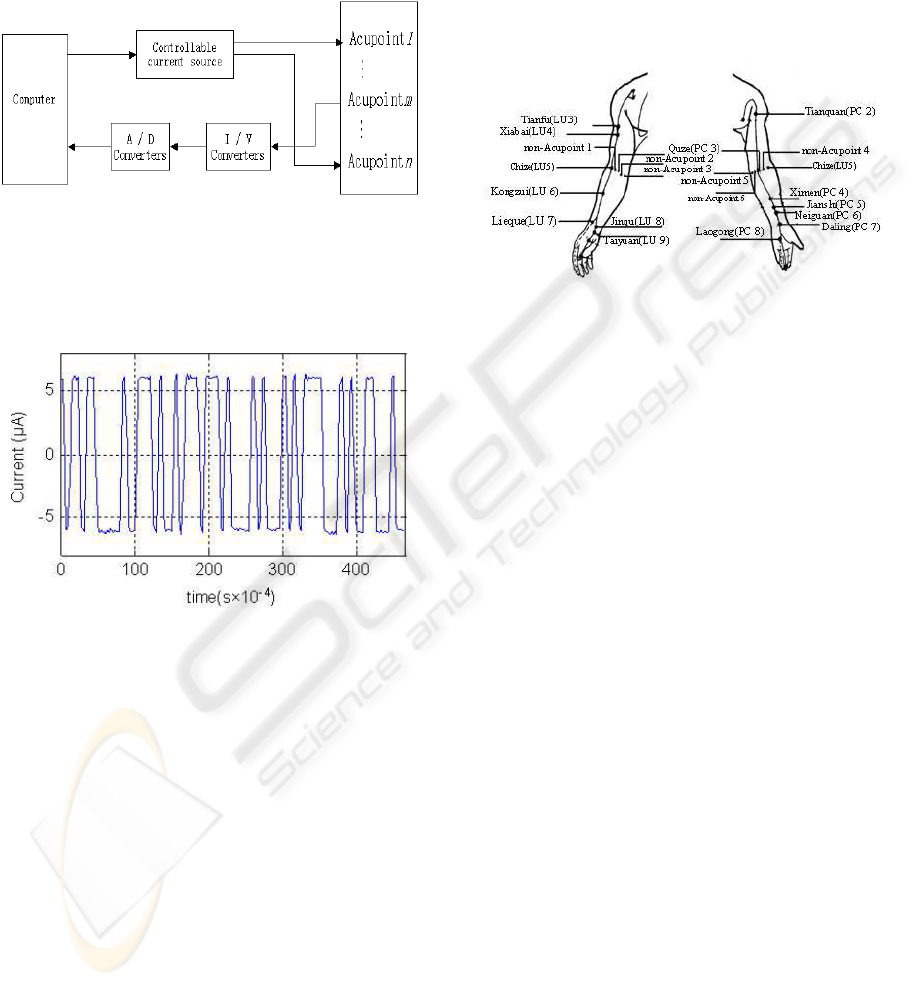
To test the signal of non-acupoint, ﬁve contrast points

of non-acupoints are selected. All the acupoints and

non-acupoints used for experiment in this paper are

shown in Figure 3.

Figure 3: The acupoints of LU, PC and non-acupoints.

Due to the limited space, we only illustrate one

of the measuring results of the responses of acupoints

and non-acupoints here. The response measured from

acupoint Chize (LU 5) is shown in Figure 4. On the

other hand, the corresponding response of the non-

acpoint 1 which is 3cm away from acupoint Chize

(LU 5) is illustrated in Figure 5. The purpose of this

investigation is to look for some differences between

the meridian system and the contrast tissue around the

meridian. From ﬁgures 4 and 5, it can be seen that

there are some differences between the responses of

the acupoint and that of the non-acupoint. In our pre-

vious works, we have applied technique of wavelet

transform to the derived signals to ﬁnd the different

characteristic of those two kinds of signals. In the fol-

lowing, we will analyze the AMRA model parameters

of the acupoint signals and contrastive non-acupoint

signals.

3 PARAMETER MODEL OF

MERIDIAN CHANNELS

According to the theory of Chinese medicine, the

meridian system contains different channels. There

are several acupoints distributed in each channel. Nat-

urally, it motivates us to investigate the characteristic

of these channels when electric signals pass by. In

this section, the auto-regressive and moving average

(ARMA) model is utilized to describe the dynamic

features of the meridian channels. It is known that

the autoregressive part of the ARMA model with a

BIODEVICES 2009 - International Conference on Biomedical Electronics and Devices

168

non-trivial denominator polynomial A(z) (’all-pole’

model) is very appropriate to describe spectra with

high and narrow peaks (Korosec, 2000), each sharp

spectrum peak corresponds to the pole located close

to unit circle at certain frequency.

Figure 4: The response of acupoint Chize (LU 5).

Figure 5: The response of non-acupoint 1.

The moving average part of the model is that,

for which a numerator polynomial B(z) exists. Pre-

dominant features of their spectra are ’valleys’, cor-

responding to the 0 near the unit circle at the spe-

ciﬁc frequencies. On many occasions, a series is

not exclusively ﬁtted to one model, but rather various

models may equally well ﬁt the series (I. Rojasa and

M.Pasadasb, 2007; Hwang, 2001). If we follow the

norms of Box and Jenkins, the model chosen is nearly

always the simplest one, i.e. that involving the fewest

terms (GEP Box and Reinsel, 1994). The ARMA

model used to describe the dynamic behaviour of the

meridian channels is described by

y(t) + a

y(t − 1) + ... + a

y(t − n

)

= b

u(t − 1) + ... + b

u(t − n

+ 1) + e(t) (1)

where y(t) is the output at time t, n

and n

are

orders of the polynomials A(z

−1

) = 1 + a

−1

+ +

−n

and B(z

−1

) = b

−1

+ + b

−n

, and e(t) is

the white-noise disturbance value. To determine the

orders of the ARMA model, the Akaike Information

Criterion (AIC) (Akaike, 1969) to perform a relative

comparison of models with different structures is ap-

pled. Smaller value of AIC indicates a better model.

Figure 6: Order identiﬁcation for acupoint signal using

AIC.

By comparing the AIC values between the differ-

ent orders of ARMA model, ﬁnally na and nb, are

respectively set to na=5 and nb=4 for the model to de-

scribe the behaviour of the transmission channel be-

tween acupoints Tianfu (LU3) and Chize (LU 5).

Figure 7 demonstrates the model validation re-

sult of the channel between acupoints Tianfu (LU3)

and Chize (LU 5). Figure 8 shows the correspond-

ing model residual. It can be seen that the obtained

model can describe the dynamic characteristic of the

measured meridian channel quite well.

Figure 7: Model validation result of the model.

The identiﬁed model coefﬁcients are illustrated in

Table 1. Based on the obtained model, the corre-

sponding poles-zeros distribution chart is shown in

Figures 9. We can see that this channel is a sta-

ble system since all the poles are located within the

unit circle. However, the response of this channel

may demonstrates some oscillation since the complex

poles are included in this model.

For comparison, the measured point 3cm away

from acupoint Chize (LU5) is deﬁned as non-acupoint

MODELING OF MERIDIAN CHANNELS

169

Figure 8: Residual of the obtained model.

Figure 9: Poles and zeroes of the model for the channel

between LU3 and LU5.

Figure 10: Poles and zeroes of the model for the channel

between LU3 and non-acupoint 1.

1. The measured data from this point is also used

to identify the model between the stimulated point

(LU3) and non-acupoint 1. The identiﬁcation proce-

dure is similar to what has been shown-above. The

obtained model parameters can also be seen in Table

Figure 10 shows the corresponding zeros and

poles distribution chart of the model to describe the

dynamic feature beyween the stimulation point LU3

and the non-acupoint 1.

From Figures 9 and 10, we note that the models,

which respectively to describe the behaviour of the

channels on the meridian system and non-meridian

system, have shown quite different characteristics.

We also identify the channel between the stimu-

lation point LU3 and the measured acupoint Xiabai

(LU4) with an ARMA model. The corresponding

zeros-poles distribution chart is shown in Figure 11.

By comparing with Figure 9, it is seen that the model

between LU 3 and LU5 and the model between LU3

and LU4 have the rather similar zeros- poles distribu-

tions.

Moreover, the locations of zeros-poles shown in

Figure 11 are also rather different from those shown

in Figure 10.

Figure 11: Poles and zeroes of the model between LU3 and

acupoint Xiabai.

The zeros-poles distribution charts of the model of

the channel between Tianquan (PC 2) and Quze (PC

3), as well as the model of the channel between Tian-

quan (PC 2) and Ximen (PC 4) are shown in Figures

12 and 13.

Figure 12: Poles and zeroes of the model for the channel

between PC2 and PC4.

Moreover, the zeros-poles distribution chart of the

model between Tianquan (PC 2) and non-acupoint 5

is illustrated in Figure 14.

From the zeros-poles distribution charts shown-

above, we know that there exist some differences be-

tween the models on the meridian channels and the

BIODEVICES 2009 - International Conference on Biomedical Electronics and Devices

170

Figure 13: Poles and zeroes of the model for the channel

between PC2 and PC5.

Figure 14: Poles and zeroes of the model between PC2 and

non-acupoint 5.

models on non-acupoints.

The obtained models can also demonstrate the dy-

namic performance of the meridian channels when

electric signals pass through. Based on the obtained

models, one can further analyze the characteristic of

the meridian systems. Especially, they would be a po-

tential ways when we intend to use them for disease

diagnosis and treatment.

Table 1: The comparison of the ARMA parameters between

acupoint and contrast non-acupoint signal.

ARMA Acupoint Non-Acupoint

Parameters signals signals

a1 -0.3819 -0.2639

a2 -0.0800 -0.4880

a3 -0.0490 -0.0687

a4 -0.0175 0.0043

a5 -0.0046 0.0131

b0 1.1158 1.2334

b1 -0.3857 -0.1057

b2 -0.0526 -0.5601

b3 -0.0721 -0.1239

4 CONCLUSIONS

In this paper, based on the electric-stimulation, the

signal characteristics of the meridian system in the

human body are presented. Based on the measured

data, the corresponding ARMA models for the merid-

ian channels between the stimulating points and the

measured acupoints are constructed. Then models be-

tween the stimulating points and the measured non-

acupoints are also identiﬁed in order to make compar-

ison.

According to the zeros-poles charts of the ob-

tained models, we can see some difference existing

in the meridian channel models and the non-accupoint

models. Some similarity seems to be observed among

the meridian channel models.

Those phenomenamay havesome potential to ﬁnd

a new way for disease diagnosis and treatment.

However, what we present in this paper is just a

primal investigation. The further research should be

implemented to see more details of the meridian sys-

tems.

ACKNOWLEDGEMENTS

This research is partially supported by Guangxi Sci-

ence Foundation (GXSF Grant No.: 0728210) and

Guilin University of Electronic Technology Research

Foundation (Z20507).

REFERENCES

Akaike, H. (1969). Fitting autoregressive models for pre-

diction. In Annals of the Institute of Statistical Math-

ematics.

F. III John, Trentini, B. T. and Erlichman, J. S. (2005). The

antinociceptive effect of acupressure in rats. In The

American Journal of Chinese Medicine. World Scien-

tiﬁc Publishing Company.

GEP Box, G. J. and Reinsel, G. (1994). Time Series Anal-

ysis: Forecasting and Control. Prentice-Hall, Engle-

wood Cliffs, New Jersey.

Hwang, H. (2001). Insights into neural-network forecasting

time series corresponding to arma (p,q) structures. In

Omega 29.

I. Rojasa, O. Valenzuelab, F. R. A. G. L. H. H. P. L. and

M.Pasadasb (2007). Soft-computing techniques and

arma model for time series prediction. In Neurocom-

puting.

J. Julia, M. T. and FACOG (1998). A modern interpreta-

tion of acupuncture and the meridian system. In 2nd

International Conference on Bioelectromagnetism.

MODELING OF MERIDIAN CHANNELS

171

Korosec, D. (2000). Parametric estimation of the continu-

ous non-stationary spectrum and its dynamics in sur-

face emg studies. In International Journal of Medical

Informatics.

W.Zhang, R. X. and Zhu, Z. (1999). The inﬂuence of

acupuncture on the impedance measured by four elec-

trodes on meridians. In Acupunct and Electro-Therap

Res. Int.J.

Yang, H. (1997). The research and application of the dy-

namic testing system for point skin resistance. In Jour-

nal of Biomedical Engineering.

BIODEVICES 2009 - International Conference on Biomedical Electronics and Devices

172