
MODELING AND SIMULATION OF BIODEGRADATION
OF XENOBIOTIC POLYMERS BASED ON EXPERIMENTAL
RESULTS
Masaji Watanabe
Graduate School of Environmental Science, Okayama University
1-1, Naka 3-chome, Tsushima, Okayama 700-8530, Japan
Fusako Kawai
Kyoto Institute of Technology, Kyoto, Japan
Keywords:
Biodegradation, Polyethylene Glycol, Mathematical modeling, Numerical simulation.
Abstract:
Biodegradation of polyethylene glycol is studied mathematically. A mathematical model for depolymerization
process of exogenous type is described. When a degradation rate is a product of a time factor and a molecular
factor, a time dependent model can be transformed into a time independent model, and techniques developed
in previous studies can be applied to the time independent model to determine the molecular factor. The time
factor can be determined assuming the exponential growth of the microbial population. Those techniques are
described, and numerical results are presented. A comparison between a numerical result and an experimental
result shows that the mathematical method is appropriate for practical applications.
1 INTRODUCTION
Biodegradation is an essential factor of the environ-
mental protection against undesirable accumulation
of xenobiotic polymers. It is particularly important
for water soluble polymers, because they are not suit-
able for recycling nor incineration. It is also impor-
tant for water-insoluble polymers, so-called plastics,
because they are not completely recycled nor incin-
erated, and a significant portion of products remains
in the environment after use. Microbial depolymer-
ization processes are generally classified into either
one of two types: exogenous type or endogenoustype.
In an exogenous depolymerization process, monomer
units are separated from the terminals of molecules
stepwise. The β-oxidation of polyethylene (PE) is an
example of exogenous depolymerization process. Mi-
crobial depolymerization processes of PE are based
on two primary factors : the gradual weight loss of
large molecules due to the β-oxidation and the di-
rect consumption or absorption of small molecules by
cells. On the other hand, one of characteristics of
endogenous depolymerization processes is the rapid
breakdown of large molecules due to internal sep-
arations to yield small molecules. The enzymatic
degradation of polyvinyl alcohol (PVA) is an exam-
ple of endogenous depolymerization process. Mathe-
matical models for those depolymerization processes
have been proposed, and those models are analyzed to
study the biodegradation of the xenobiotic polymers.
In this paper, the study of exogenous depolymer-
ization processes is continued to cover the biodegra-
dation of polyethylene glycol (PEG). PEG is one of
polyethers which are represented by the expression
HO(R-O)
n
H, e.g., PEG: R= CH
2
CH
2
, polypropylene
glycol (PPG): R = CH
3
CHCH
2
, polytetramethylene
glycol (PTMG): R = (CH
2
)
4
(Kawai, 1993). Those
polymers are utilized for constituents in a number of
products including lubricants, antifreeze agents, inks,
and cosmetics. They are either water soluble or oily
liquid. Some portion of products are eventually dis-
charged through sewage to be processed, while some
others enter streams, rivers, and coastal areas. and
therefore it is especially important to evaluate their
biodegradability. PEG is produced more than any
other polyethers, and the major part of production is
consumed in production of nonionic surfactants. PEG
is depolymerized by releasing C
2
compounds, either
aerobically or anaerobically (Kawai, 1995; Kawai,
2002; Kawai and Xenobiotic Polymers, 2002) (Fig-
ure 1).
High performanceliquid chromatography(HPLC)
25
Watanabe M. and Kawai F. (2009).
MODELING AND SIMULATION OF BIODEGRADATION OF XENOBIOTIC POLYMERS BASED ON EXPERIMENTAL RESULTS.
In Proceedings of the International Conference on Bio-inspired Systems and Signal Processing, pages 25-34
DOI: 10.5220/0001433100250034
Copyright
c
SciTePress

CH
2
HOCH
2
CH O
CH
2
O
R
H
Cobalamin
CH
2
CH
3
CH O
CH
2
O R
OH
HOCH
2
CH
3
CHO
CH
2
O
R
+
HO(CH
2
CH
2
O)
n
CH
2
CH
2
OH
HO(CH
2
CH
2
O)
n
CH
2
CHO
(1)
(2)
HO(CH
2
CH
2
O)
n
CH
2
COOH
(3)
HOOCCH
2
O(CH
2
CH
2
O)
n-1
CH
2
COOH
CHOCOOH
HO(CH
2
CH
2
O)
n-1
CH
2
OH
HO(CH
2
CH
2
O)
n-1
CH
2
COOH
(1) PEG dehydrogenase
(2) PEG-aldehyde dehydrogenase
(3) PEG-carboxylate dehydrogenase
Figure 1: Anaerobic metabolic pathway (left) and Aerobic metabolic pathway (right) of PEG.
patterns were introduced into analysis of an exoge-
nous depolymerization model to set the weight distri-
bution of PEG with respect to the molecular weight
before and after cultivation of a microbial consortium
E1 (Figure 2).
In the previous studies (Watanabe and Kawai,
2004), the degradation rate was assumed to be inde-
pendent of time. The time dependent degradation rate
was considered in a recent study assuming a logis-
tic growth in a microbial population (Watanabe and
Kawai, 2005), and using a cubic spline to take the
change of microbial population into considerateion
(Watanabe and Kawai, 2007). In this paper, the math-
ematical study of biodegradation of PEG is contin-
ued with the time dependent degradation rate incor-
porated into the exogenous depolymerization model.
A change of variable reduces the model into the one
for which the degradation rate is time independent.
The techniques developed previously were applied to
solve an inverse problem to determine the time in-
dependent degradation rate for which the solution of
an initial value problem satisfies not only the initial
weight distribution but also the weight distribution af-
ter cultivation. The time factor was determined by as-
suming the exponential growth of the microbial pop-
ulation. Once the degradation rate was found, the
transition of the weight distribution was simulated by
solving the initial value problem numerically.
2 MODEL WITH TIME
DEPENDENT DEGRADATION
RATE
The PE biodegradation model (1) is based on two
essential factors: the gradual weight loss of large
molecules due to terminal separations (β-oxidation)
and the direct consumption of small molecules by
cells (Kawai et al., 2002; Watanabe et al., 2003;
Kawai et al., 2004).
dw
dt
(t,M) = −α(M)w(t,M)
+β(M+ L)
M
M + L
w(t,M + L).
(1)
Here t and M represent the time and the molecular
weight respectively. Let a M-molecule be a molecule
with molecular weight M. Then w(t,M) represents
the total weight of M-molecules present at time t.
Note that w(t,M) is a function of time variable t, and
that it also depends on the parameter M. The param-
eter L represents the amount of the weight loss due to
the β-oxidation. The variable y denotes w(t,M + L),
and it is the total weight of (M + L)-molecules present
at time t. The function α(M) denotes ρ(M) + β(M),
where the function ρ(M) represents the direct con-
sumption rate, and the function β(M) represents the
rate of the weight conversion from the class of M-
molecules to the class of (M − L)-molecules due to
the β-oxidation. The left-hand side of the equation
(1) represents the rate of change in the total weight
BIOSIGNALS 2009 - International Conference on Bio-inspired Systems and Signal Processing
26
0
0.005
0.01
0.015
0.02
0.025
3.1 3.2 3.3 3.4 3.5 3.6 3.7 3.8 3.9 4 4.1 4.2
COMPOSITION (%)
LOG M
BEFORE CULTIVATION
AFTER 1-DAY CULTIVATION
AFTER 3-DAY CULTIVATION
AFTER 5-DAY CULTIVATION
AFTER 7-DAY CULTIVATION
AFTER 9-DAY CULTIVATION
Figure 2: Weight distribution of PEG before and after cultivation of a microbial consortium E1 for one day and three days.
of M-molecules. The first term on the right-hand side
of the equation (1) represents the amount lost by the
direct consumption and the β-oxidation in the total
weight of M-molecules per unit time, and the second
term represents the amount gained by the β-oxidation
of (M + L)-molecules per unit time. The mathemat-
ical model (1) was originally developed for the PE
biodegradation, but it can also be viewed as a gen-
eral biodegradation model involving exogenous de-
polymerization processes. In the exogenous depoly-
meization of PEG, a PEG molecule is first oxidized
at its terminal, and then an ether bond is split. It fol-
lows that L = 44 (CH
2
CH
2
O) in the exogenous de-
polymerization of PEG. PEG molecules studied here
are lagre molecules that can not be absorbed directly
through membrene into cells. Then ρ(M) = 0, and
α(M) = β(M).
The equation (1) is appropriate for the depolymer-
ization processes over the period after the microbial
population is fully developed. However the change of
microbial population should be taken into considera-
tion for the period in which it is still in a developing
stage, and the degradation rate should be time
dependent. Then the exogenous depolymerization
model becomes
dw
dt
(t,M) = −β(t,M) w(t,M)
+β(t,M + L)
M
M + L
w(t,M + L).
(2)
to model the change of weight distribution of PEG.
The solution x = w(t,M) of (2) is associated with the
initial condition:
w(0,M) = f (M), (3)
where f (M) is some prescribed function that repre-
sents the initial weight distribution. Given the the
degradation rate β(t,M), the equation (2) and the ini-
tial condition (3) form an initial value problem to find
the unknown function w(t,M).
A time factor of the degradation rate such as mi-
crobial population, dissolved oxygen, or tempera-
ture should affect molecules regardless of their sizes.
Then the dependence of the degradation rate on those
time factors must be uniform over all the molecular
weight classes, and the degradation rate should be a
product of a time dependent part σ(t) that represents
MODELING AND SIMULATION OF BIODEGRADATION OF XENOBIOTIC POLYMERS BASED ON
EXPERIMENTAL RESULTS
27

the magnitude of degradability, and a molecular de-
pendent part λ(M) that represents the molecular de-
pendence of degradability:
β(t,M) = σ(t)λ(M). (4)
Let
τ =
Z
t
0
σ(s) ds, (5)
and
W (τ,M) = w(t,M),
X = W (τ,M) ,
Y = W (τ,M + L).
Then
dX
dτ
=
dx
dt
dt
dτ
=
1
σ(t)
dx
dt
.
It follows that
dX
dτ
= −λ(M) X + λ(M + L)
M
M + L
Y. (6)
This equation governs the transition of weight dis-
tribution W (t,M) which changes with the time in-
dependent or time averaged degradation rate λ(M).
Given the initial weight distribution f (M), The solu-
tion of the initial value problem is the solution of the
equation (6) subject to the initial condition
W (0,M) = f (M). (7)
The solution of the inverse problem is the degradation
rate λ(M) for which the solution of the initial value
problem (6), (7) also satisfies the final condition
W (T ,M) = g(M). (8)
When the solution W (τ,M) of the initial value prob-
lem (6), (7) satisfies this condition, the solution
w(t,M) of the intiail value problem (2), (3) satisfies
the condition
w(T,M) = g(M), (9)
where
T =
Z
T
0
σ(s) ds (10)
The inverse problem consisting of the equation (6)
and the conditions (7) and (8) was solved numerically
with techniques developed in previous studies. Fig-
ure 3 shows the graph of the function λ(M) based on
the weight distribution before and after cultivation for
three days (Watanabe and Kawai, 2004).
3 TIME FACTOR OF
DEGRADATION RATE
A microbial population grows exponentially in a de-
veloping stage. Since the increase of biodegradability
results from increase of microbial population, it is ap-
propriate to assume that the time factor of the degra-
dation rate σ(t) is an exponential function of time:
σ(t) = e
at+b
. (11)
Then in view of the equation (5)
τ =
Z
t
0
σ(s) ds =
Z
t
0
e
as+b
ds =
e
b
a
e
at
− 1
.
Suppose that the weight distribution is given at t =
T
1
and t = T
2
, where 0 < T
1
< T
2
, and let
T
1
=
Z
T
1
0
σ(s) ds, (12)
T
2
=
Z
T
2
0
σ(s) ds (13)
It follows that
σ(t) = e
b
e
at
=
aT
1
e
at
e
aT
1
− 1
(14)
and
τ = T
1
e
at
− 1
e
aT
1
− 1
(15)
Now the equation (13) leads to
T
2
= T
1
e
aT
2
− 1
e
aT
1
− 1
,
which is equivalent to the equation
h(a) = 0, (16)
where
h(a) =
e
aT
2
− 1
e
aT
1
− 1
−
T
2
T
1
.
Since
h
′
(a) =
T
2
e
aT
2
e
aT
1
− 1
− T
1
e
aT
1
e
aT
2
− 1
(e
aT
2
− 1)
2
,
h
′
(a) > 0 if and only if
T
1
e
aT
1
e
aT
2
− 1
<
T
2
e
aT
2
e
aT
2
− 1
For x > 0
q(x) =
xe
ax
e
ax
− 1
=
x
1− e
−ax
Then
q
′
(x) =
1− e
−ax
− axe
−ax
(1− e
−ax
)
2
=
e
−ax
(e
ax
− 1− ax)
(1− e
−ax
)
2
> 0.
BIOSIGNALS 2009 - International Conference on Bio-inspired Systems and Signal Processing
28

0
20
40
60
80
100
120
140
160
180
200
3.1 3.2 3.3 3.4 3.5 3.6 3.7 3.8 3.9 4 4.1 4.2
DEGRADATION RATE [1/DAY]
LOG M
PEG EXOGENOUS DEGRADATION RATE
Figure 3: Degradation rate based on the weight distribution of PEG before and after cultivation of a microbial consortium E1
for three days.
It follows that the q(x) is a strictly increasing
function, and it follows that h
′
(a) > 0.
It is easily seen that
lim
a→∞
h(a) = ∞
Suppose that
T
2
T
1
<
T
2
T
1
(17)
Then by L’Hospital’s rule
lim
a→0+
h(a) = lim
a→0+
e
aT
2
− 1
e
aT
1
− 1
−
T
2
T
1
= lim
a→0+
e
aT
2
− 1
e
aT
1
− 1
−
T
2
T
1
= lim
a→0+
T
2
e
aT
2
T
1
e
aT
1
−
T
2
T
1
=
T
2
T
1
−
T
2
T
1
< 0
(18)
It follows that the condition (17) is a necessary and
sufficient condition for the equation (16) to have a
unique positive solution.
In order to determine a and b, the values of T
1
,
T
2
, T
1
, and T
2
must be set. Let T
1
= T
1
= 3. The
initial value problem (6), (7) was solved numerically
with the degradation whose graph is shown in Figure
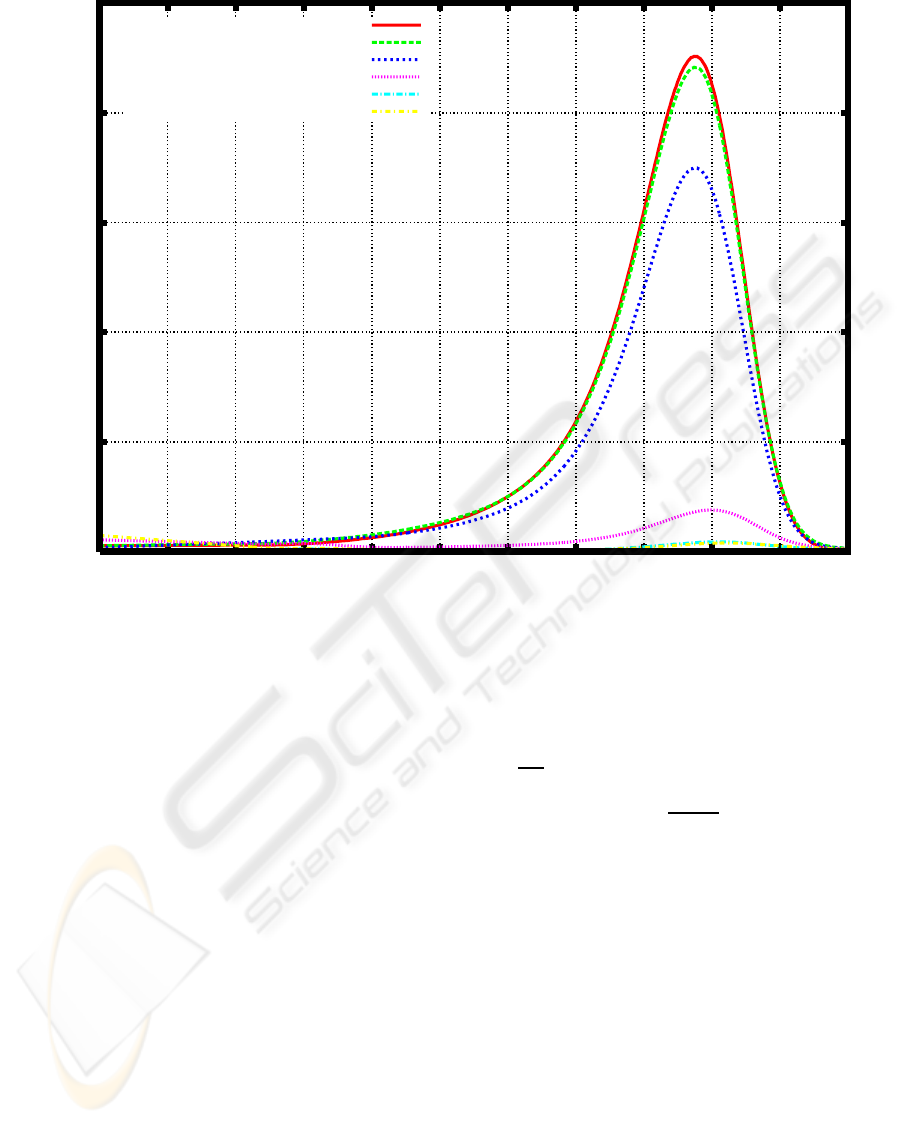
3 to find the weight distribution at τ = 30 (Figure 4).
Figure 4 also shows the weight distribution after cul-
tivation for five days.
Figure 4 shows that it is appropriate to set T
2
= 5
and T
2
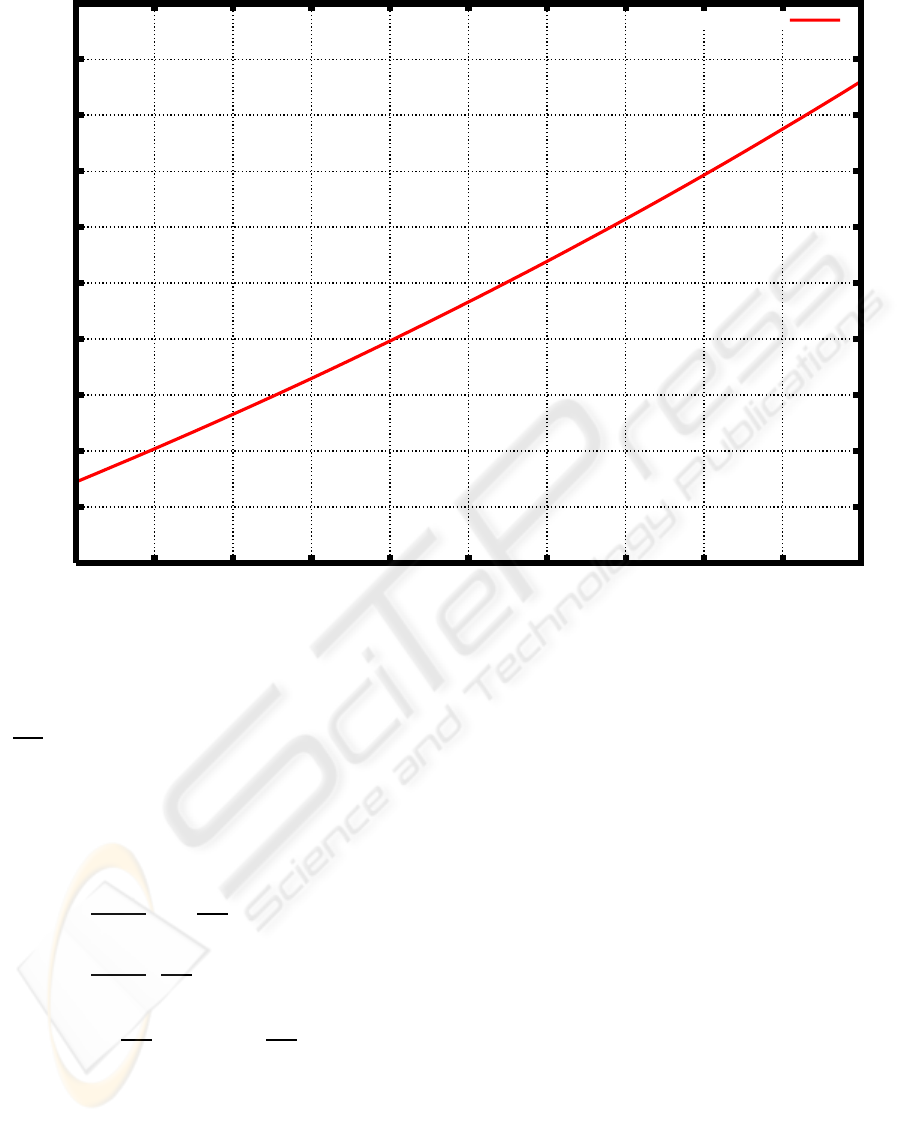
= 30. Figure 5 shows the graph of h(a) with
those values of parameters.
Figure 5 shows that there is a unique solution of
the equation (16). It was solved numerically with the
Newton’s method, and a numerical solution, which
was approximately equal to 1.136176 was found.
MODELING AND SIMULATION OF BIODEGRADATION OF XENOBIOTIC POLYMERS BASED ON
EXPERIMENTAL RESULTS
29

0
0.005
0.01
0.015
0.02
0.025
3.1 3.2 3.3 3.4 3.5 3.6 3.7 3.8 3.9 4 4.1 4.2
COMPOSITION (%)
LOG M
AFTER 5-DAY CULTIVATION
SIMULATION: 30 DAY
Figure 4: Weight distribution of PEG after cultivation for 30 days according to the time independent model based on the initial
value problem (6), (7), and the degradation rate shown in Figure 3. The experimental result obtained after cultivation for 5
days is also shown.
4 SIMULATION WITH TIME
DEPENDENT DEGRADATION
RATE
Once the degradation rate σ(t)λ(M) are given, the
initial value problem (2) and (3) can be solved di-
rectly to see how the numerical results and the ex-
perimental results agree. Here the initial value prob-
lem was solved numerically with techniques base on
previous results (Watanabe et al., 2003; Kawai et al.,
2004; Watanabe et al., 2004).
Choose a positive integer N and set
∆M =
b− a
N
M
i
= a + i∆M, i = 0, 1,2,· · · ,N.
An approximate solution of the differen-
tial equation (1) at M = M
i
is denoted by
w
i
= w
i
(t) (i = 0,1,2,· · · ,N). There is a non-
negative integer K and a constant R such that
L = K∆M + R, 0 ≤ R < ∆M, and that the inequalities
M
i+K
≤ M
i
+ L < M
i+K+1
hold. Then approximate values of w(t, M
i
+ L) and
β(M
i
+ L) can be obtained by using the approxima-
tions
w(t,M
i
+ L) ≈
1−
R
∆M
w(t,M
i+K
)
+
R
∆M
w(t,M
i+K+1
),
λ(M
i
+ L) ≈
1−
R
∆M
λ(M
i+K
)
+
R
∆M
λ(M
i+K+1
).
Substituting these expressions in the differential
equation (2) and setting M = M
i
, we obtain the linear
BIOSIGNALS 2009 - International Conference on Bio-inspired Systems and Signal Processing
30
-3
-2.5
-2
-1.5
-1
-0.5
0
0.5
1
1.5
2
1 1.02 1.04 1.06 1.08 1.1 1.12 1.14 1.16 1.18 1.2
h(a)
a
Graph of h(a)
Figure 5: Graph of h(a) with T
1
= T
1
= 3, T
2
= 5 and T
2
= 30.
system:
dw
i
dt
= σ(t) (−α
i
w
i
+ β
i
w
i+K
+ γ
i
w
i+K+1
),
i = 0, 1,2,· · · , N.
(19)
The coefficients α
i
, β
i
, and γ
i
are given by
α
i
= λ(M
i
),
β
i
= φ
i
M
i
M
i
+ L
1−
R
∆M
,
γ
i
= φ
i
M
i
M
i
+ L
·
R
∆M
,
φ
i
=
1−
R
∆M
λ(M
i+K
) +
R
∆M
λ(M
i+K+1
).
Approximate values of the degradation rates
λ(M
i
) can be obtained from the numerical solution
of the inverse problem by the linear approximation.
For all sufficiently large M, the oxidation rate be-
comes 0. In particular, we may assume that the last
two terms on the right-hand side of the equation (19)
are absent when i+ K exceeds N, so that the system
(19) becomes a closed system to be solved for un-
known functions w
i
= w
i
(t), i = 0,1,2,. .. ,N. In view
of the condition (3), these functions are subject to the
initial condition
w
i
(0) = f
i
= f (M
i
). (20)
Given the initial weight distribution shown in Fig-
ure 2, the degradation rate λ(M) shown in Figure
3, and the function σ(t) given by the equation (14)
with the value of a obtained numerically, the ini-
tial value problem (19) and (20) was solved numeri-
cally implementingthe forth-orderAdams-Bashforth-
Moulton predictor-corrector in PECE mode in con-
junction with the Runge-Kutta method to generate
approximate solutions in the first three steps (Lam-
bert, 1973) by using N = 10000, and a time interval
∆t = 5/24000. Figure 6 shows the transition of the
weight distribution during cultivation of the microbial
consortium E-1 for five days.
Figure 7 shows the numerical result and the ex-
perimental results for the weight distribution after one
day cultivation of the microbial consortium E1.
MODELING AND SIMULATION OF BIODEGRADATION OF XENOBIOTIC POLYMERS BASED ON
EXPERIMENTAL RESULTS
31

0
0.005
0.01
0.015
0.02
0.025
3.1 3.2 3.3 3.4 3.5 3.6 3.7 3.8 3.9 4 4.1 4.2
COMPOSITION (%)
LOG M
BEFORE CULTIVATION
AFTER 5-DAY CULTIVATION
SIMULATION: 1 DAY
SIMULATION: 2 DAY
SIMULATION: 3 DAY
SIMULATION: 4 DAY
SIMULATION: 5 DAY
Figure 6: The weight distribution of PEG before and after 5-day cultivation, and the transition of the weight distribution based
on the initial value problem (2), (3) with σ(t) = e
at+b
, a ≈ 1.136176, b = ln
aT
1
/
e
aT
1
− 1
, T
1
= T
1
= 3.
5 DISCUSSION
Early studies of biodegradation of xenobiotic poly-
mers are found in the second half of the 20th cen-
tury. It was found that the linear paraffin molecules
of molecular weight up to 500 were utilized by sev-
eral microorganisms (Potts et al., 1972). Oxida-
tion of n-alkanes up to tetratetracontane (C
44
H
90
,
mass of 618) In 20 days was reported (Haines et al.,
1974). Biodegradation of polyethylene was shown by
measurement of
14
CO
2
generation (Albertsson et al.,
1987). The weight distribution of polyethylene be-
fore and after cultivation of the fungus Aspergillus
sp. AK-3 for 3 weeks was introduced into analysis
based on the time dependent exogenous depolymer-
ization model. The transition of weight distribution
for 5 weeks was simulated with the degradation rate
based on the initial weight distribution and the weight
distribution after 3 weeks of cultivation. The numer-
ical result was found to be acceptable in comparison
with an experimental result (Watanabe et al., 2004).
The result shows that the microbial population was
fully developed in 3 weeks, and that the biodegrada-
tion was with the constant rate.
The degradation rate changed over the cultivation
period in the depolymerizationprocesses of PEG. The
development of microbial population accounts for the
increase of degradability overthe first five days of cul-
tivation. In a depolymerization process where the mi-
crobial population becomes an essential factor, it is
necessary to consider the dependence of the degrada-
tion rate on time. The numerical results based on the
time dependent exogenous depolymerization model
show reasonable agreement with the experimental re-
sults. Those results show that it is appropriate to as-
sume that the degradation rate is a product of a time
factor and a molecular factor. It has also been shown
that the molecular factor can be determined by the
weight distribution before and after cultivation exper-
imentally. In the environment or sewer disposal, the
time factor should also depends on other factors such
as temperature or dissolved oxygen. Once those es-
sentials are incorporated into the time dependent fac-
tor, the time dependent exogenous depolymerization
BIOSIGNALS 2009 - International Conference on Bio-inspired Systems and Signal Processing
32

0
0.005
0.01
0.015
0.02
0.025
3.1 3.2 3.3 3.4 3.5 3.6 3.7 3.8 3.9 4 4.1 4.2
COMPOSITION (%)
LOG M
AFTER 1-DAY CULTIVATION
SIMULATION: 1 DAY
Figure 7: The weight distribution of PEG after 1-day cultivation, and the weight distribution based on the initial value problem
(2), (3) with σ(t) = e
at+b
, a ≈ 1.136176, b = ln
aT
1
/
e
aT
1
− 1
, T
1
= T
1
= 3, t = 1.
model and the techniques based on the model should
be applicable to assess biodegradability of xenobiotic
polymers.
REFERENCES
Potts, J.E., Clendinning, R.A., Ackart W.B. and Niegishi,
W.D., The biodegradability of synthetic polymers,
Polym Preprints 1972; 13; 629-34.
Haines, J.R. and Alexander, M., Microbial degradation of
high-molecular-weight alkanes, Appl Microbiol 1974;
28; 1084-5.
Albertsson, A-C, Andersson SO and Karlsson, S, The
mechanism of bioidegradation of plyethylene, Polym
Degrd Stab 1987; 18; 73-87.
Fusako Kawai, Masaji Watanabe, Masaru Shibata, Shi-
geo Yokoyama, Yasuhiro Sudate, Experimental anal-
ysis and numerical simulation for biodegradability of
polyethylene, Polymer Degradation and Stability 76
(2002) 129-135.
Masaji Watanabe, Fusako Kawai, Masaru Shibata, Shigeo
Yokoyama, Yasuhiro Sudate, Computational method
for analysis of polyethylene biodegradation, Journal
of Computational and Applied Mathematics, Volume
161, Issue 1, 1 December 2003, 133-144.
Fusako Kawai, Biodegradability and chemical structure of
polyethers, Kobunshi Ronbunshu, 50(10), 775-780
(1993) (in Japanese).
Fusako Kawai, Breakdown of plastics and polymers by
microorganisms, Advances in Biochemical Engineer-
ing/Biotechnology, Vol. 52, 151-194 (1995).
F. Kawai, Microbial degradation of polyethers, Applied Mi-
crobiology and Biotechnology (2002) 58:30-38.
Lambert, J. D., Computational Methods in Ordinary Differ-
ential Equations, John Wiley Sons, Chichester, 1973.
Fusako Kawai, Masaji Watanabe, Masaru Shibata, Shigeo
Yokoyama, Yasuhiro Sudate, Shizue Hayashi, Com-
parative study on biodegradability of polyethylene
wax by bacteria and fungi, Polymer Degradation and
Stability 86 (2004), 105-114.
Masaji Watanabe, Fusako Kawai, Masaru Shibata, Shigeo
Yokoyama, Yasuhiro Sudate, Shizue Hayashi, Analyt-
ical and computational techniques for exogenous de-
polymerization of xenobiotic polymers, Mathematical
Biosciences 192 (2004) 19-37.
F. Kawai, Xenobiotic polymers, in: T. Imanaka, ed., Great
Development of Microorganisms, (NTS. Inc., Tokyo,
2002) 865-870 (in Japanese).
MODELING AND SIMULATION OF BIODEGRADATION OF XENOBIOTIC POLYMERS BASED ON
EXPERIMENTAL RESULTS
33

M. Watanabe, F. Kawai, Numerical simulation of microbial
depolymerization process of exogenous type, Proc.
of 12th Computational Techniques and Applications
Conference, CTAC-2004, Melbourne, Australia in
September 2004, Editors: Rob May and A. J. Roberts,
ANZIAM J. 46(E) pp.C1188–C1204, 2005. (http://
anziamj.austms.org.au/V46/CTAC2004/Wata)
M. Watanabe, F. Kawai, Mathematical study of the
biodegradation of xenobiotic polymers with ex-
perimental data introduced into analysis, Proceed-
ings of the 7th Biennial Engineering Mathemat-
ics and Applications Conference, EMAC-2005,
Melbourne, Editors: Andrew Stacey and Bill
Blyth and John Shepherd and A. J. Roberts,
ANZIAM J. 47 pp.C665–C681, 2007. (http:// anzi-
amj.austms.org.au/V47EMAC2005/Watanabe)
Masaji Watanabe, Fusako Kawai, Numerical study of
biodegradation of xenobiotic polymers based on ex-
ogenous depolymerization model with time dependent
degradation rate, Journal of the Faculty of Environ-
mental Science and Technology, Okayama University,
Vol. 12, No. 1, pp. 1-6, March 2007.
BIOSIGNALS 2009 - International Conference on Bio-inspired Systems and Signal Processing
34
