A MULTIVARIATE STATISTICAL ANALYSIS OF MUSCULAR

BIOPOTENCIAL FOR HUMAN ARM MOVEMENT

CHARACTERIZATION

Giuliano Alves da Silva, Maria Cláudia Ferrari de Castro and Carlos Eduardo Thomaz

Department of Electrical Engineering, Centro Universitário da FEI

Av. Humberto A.C. Branco, 3972, São Bernardo do Campo, São Paulo, CEP 09850-901, Brazil

Keywords: Electromyography, Biceps, Triceps, Linear Transformation, PCA, MLDA, Bhattacharyya Distance.

Abstract: Pattern recognition of electromyographic signals consists of a hard task due to the high dimensionality of

the data and noise presence on the acquired signals. This work intends to study the data set as a multivariate

pattern recognition problem by applying linear transformations to reduce the data dimensionality. Five

volunteers contributed in a previous experiment that acquired the myoelectrical signals using surface

electrodes. Attempts to analyse the groups of acquired data by means of descriptive statistics have shown to

be inconclusive. This works shows that the use of multivariate statistical techniques such as Principal

Components Analysis (PCA) and Maximum uncertainty Linear Discriminant Analysis (MLDA) to

characterize the acquired set of signals through low dimensional scatter plots provides a new understanding

of the data spread, making easier its analysis. Considering the arm horizontal movement and the acquired

set of data used in this research, a multivariate linear separation between the patterns of interest quantified

by the distance of Bhattacharyya suggests that it’s possible not only to characterize the angular joint

position, but also to confirm that different movements recruit similar amounts of energy to be executed.

1 INTRODUCTION

The human movement characterization represents a

great challenge and a relatively new field in the

scientific investigation. Several techniques have

been used in the attempt to describe and classify

these movements (Kleissen et al., 1998; Bittar and

Castro, 2008).

The study of muscular bio-potentials has been

developed impelled by the diagnosis of

neuromuscular disturbances and by the development

of mechanical prostheses for amputees. The

myoelectric signal, through the electromyography,

helps to describe, standardize and define the

operation of the muscular movement. The

electromyography consists of acquiring and

registering the electric signals emitted by the

muscular cells.

Electric signals, generated by motor units in the

skeleton muscles, control the position and the

movements of the limbs, while traveling between the

muscles and the peripheral/central nervous system

(Henneberg, 2000). By acquiring and studying these

signals through the electromyography, it’s possible

to determine patterns of interest and use such

discriminative information to control a wide variety

of devices. Unfortunately this information is not

totally reliable due to a great susceptibility to noise,

redundancy, and the small sample size inherent to

the acquired data set.

This paper introduces some techniques that aim

to improve the understanding and reliability of the

acquired data set by applying multivariate linear

transformations such as Principal Components

Analysis (PCA) (Fukunaga, 1990) and Maximum

uncertainty Linear Discriminant Analysis (MLDA)

(Thomaz et al., 2005). Experiments mixing the

signals provided by the biceps and triceps, in an

experience that intends to identify the angular

position of the arm, have shown that it’s possible to

have a good and reliable separation of myoelectric

signals for further classification.

227

Silva G., Castro M. and Thomaz C. (2009).

A MULTIVARIATE STATISTICAL ANALYSIS OF MUSCULAR BIOPOTENTIAL FOR HUMAN ARM MOVEMENT CHARACTERIZATION.

In Proceedings of the International Conference on Bio-inspired Systems and Signal Processing, pages 227-232

DOI: 10.5220/0001433802270232

 SciTePress

2 EXPERIMENTS

AND METHODS

2.1 Experiments

For the extraction and analysis of myoelectric

signals used in this experiment, five volunteers were

submitted to tests in a previous research that

evaluated the contribution of the muscles biceps and

triceps during voluntary flexion and extension elbow

movements (Bittar and Castro, 2008).

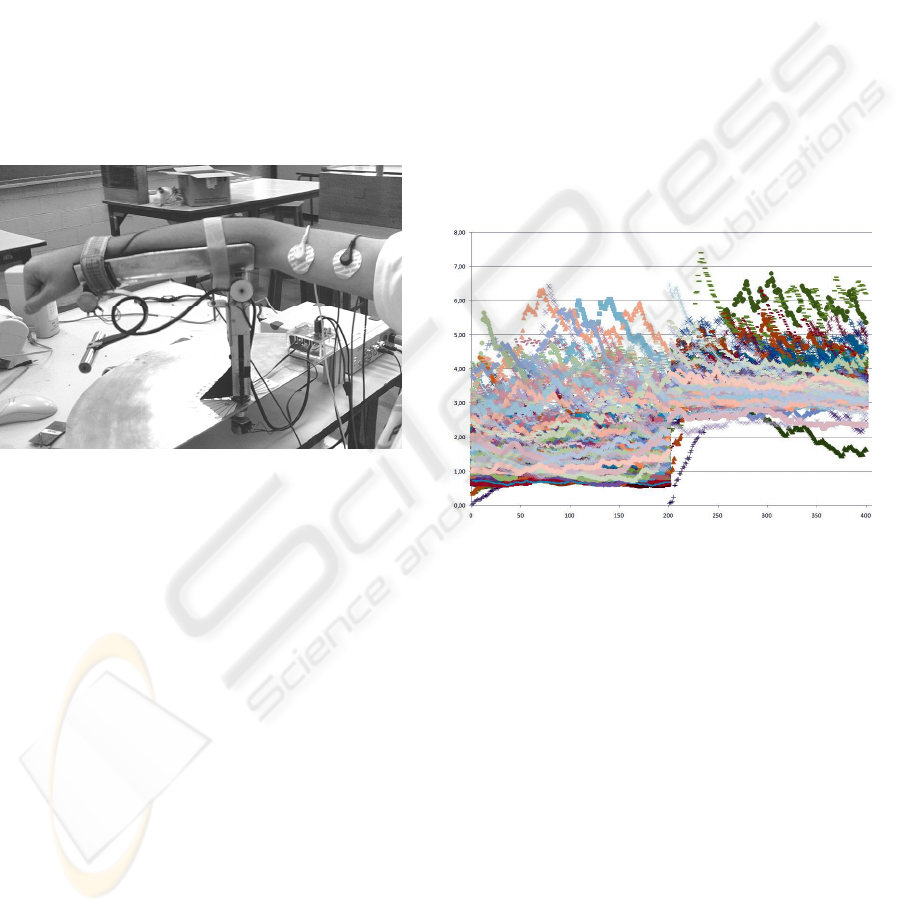
Figure 1 illustrates the device used in the

experiment, developed to minimize the interferences

in the movement performed by the volunteer and

guarantee the angular position of the arm, making

easier the control over the acquired data.

Figure1: Horizontal myographic signals acquisition.

Each volunteer was submitted to 3 types of tests

repeated 3 times in the vertical and horizontal plans.

In this work, we only consider the tests in the

horizontal plan, according to the following

description:

- Test 1 (BT1): The first test consists of moving

the arm in a 10° shift on every 3 seconds going to

90° and returning to the extension position by the

same way. This test generated a subset of data, here

called BT1, which have been labeled as 3 different

groups of signals: 0° to 10°, 40° to 50° and 80° to

90°;

- Test 2 (BT2): In the second test, the volunteer

repeated the movement from 0° to 90°, but this time

without pauses, in a continuous way and in the space

of ten seconds. This test generated the BT2 subset of

data, which have been labeled accordingly to the

following 3 groups of signals: 0° to 10°, 40° to 50°

and 80° to 90°;

- Test 3 (BT3): In the third test, the movement

should be done moving the arm from the initial point

in a 10° shift and returning to the origin and

repeating again from the origin to 20° and back, so

forth until achieving 90°. This test generated the

BT3 subset data, which have been labeled

accordingly to the following 3 groups of signals: 0°

to 10°, 0° to 50° and 0 to 90°.

The myoelectric signals were tabulated to

simplify the data set manipulation. A data set BTG

(BT1+BT2+BT3) was created considering the

simultaneous analysis of biceps and triceps signals

to characterize the arm angular position. Figure 2

shows a representation of the BTG group, obtained

from the combined signals of triceps and biceps

muscles in movements from 0° to 10°, 40° to 50°

and 80° to 90° (BT1+BT2) and 0° to 10°, 0° to 50°

and 0° to 90° (BT3), through a dispersion graph. It

can be seen that due to the high dimensionality of

the data and noise presence on the acquired signals,

the characterization of the patterns of interest is a

challenging multivariate data analysis task.

Figure 2: BTG biceps (left) and triceps (right) signals.

2.2 Methods

In statistical pattern recognition, a myographic

signal with n variables or parameters can be treated

as a point in an n-dimensional space called the

original space. The coordinates of this point

represent the values of each variable of the signal

and form a high dimensional vector

[

]

xxxx ,,,

…=

, where n>>1. Since n-

dimensional myographic signals are highly

redundant, we can project such multivariate data

onto a lower dimensional space without significant

loss of information. In this section, we describe the

multivariate statistical techniques used in this work

to analyze and characterize the acquired set of

signals through low dimensional linear

transformations.

BIOSIGNALS 2009 - International Conference on Bio-inspired Systems and Signal Processing

228

2.2.1 Principal Components Analysis (PCA)

PCA is a feature extraction procedure concerned

with explaining the covariance structure of a set of

variables through a small number of linear combina-

tions of these variables. It is a well-known statistical

technique that has been used in several pattern

recognition problems, especially for dimensionality

reduction. A comprehensive description of this

multivariate statistical analysis method can be found

in (Fukunaga, 1990).

Let an

N x n training set matrix

composed of

N input signals with n variables.

This means that each column of matrix

represents the values of a particular variable

observed all over the

N signals. Let this data matrix

have covariance matrix S with respectively

and

eigenvector and eigenvalue matrices, that is,

Λ=SPP

. (1)

It is a proven result that the set of m (

≤

)

eigenvectors of

S , which corresponds to the m

largest eigenvalues, minimizes the mean square

reconstruction error over all choices of

orthonormal basis vectors (Fukunaga, 1990). Such a

set of eigenvectors that defines a new uncorrelated

coordinate system for the training set matrix

known as the principal components.

Therefore, although n variables are required to

reproduce the total variability (or information) of the

sample

, much of this variability can be

accounted for by a smaller number m of principal

components. That is, the m principal components

can then replace the initial n variables and the

original data set, consisting of

N measurements on

variables, is reduced to a data set consisting of N

measurements on

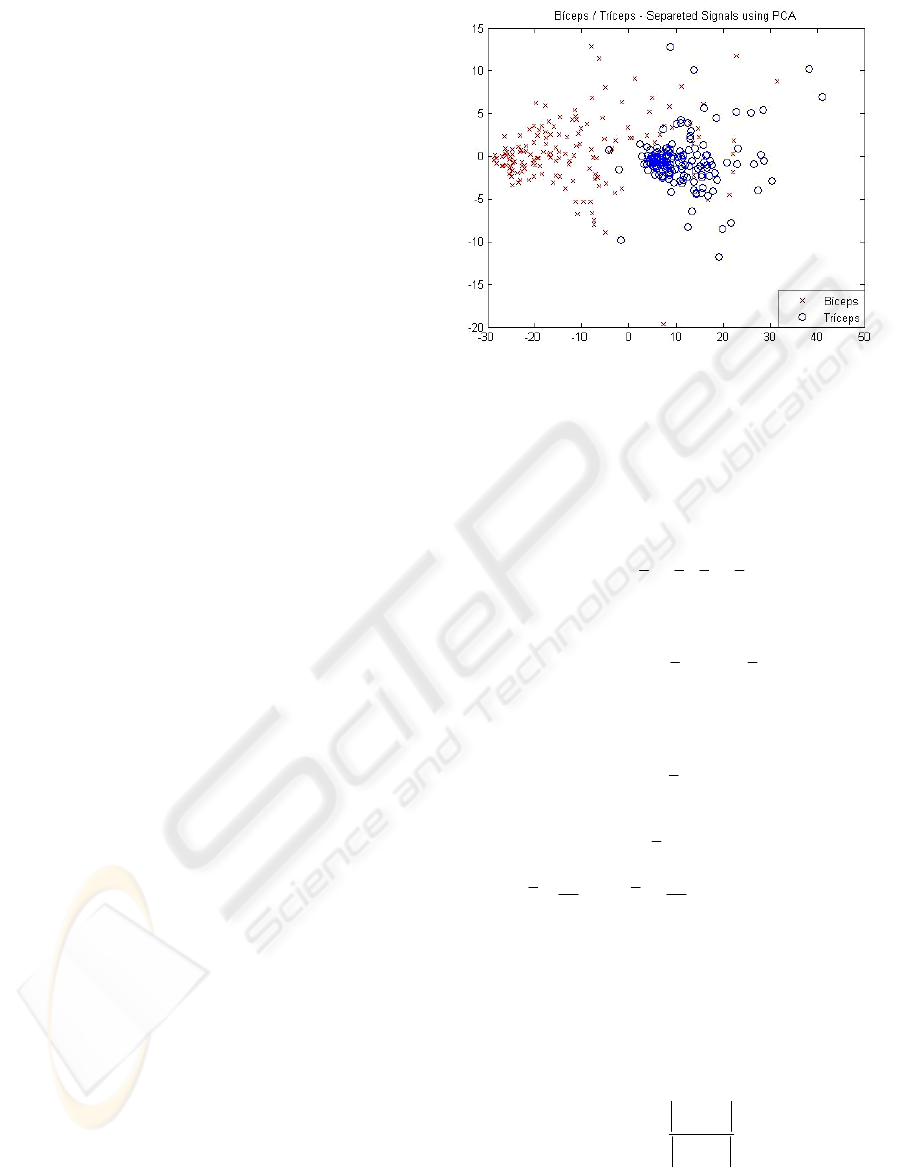
principal components. Figure 3

shows the representation of the BTG data set

focusing on the analysis of the biceps and triceps

signals on the first two principal components (m=2).

However, since PCA explains the covariance

structure of all the data its most expressive

components, that is, the first principal components

with the largest eigenvalues, do not necessarily

represent important discriminant directions to

separate groups of patterns.

2.2.2 Maximum Uncertainty LDA (MLDA)

A common practice to identify the important linear

directions for separating groups of patterns is to use

Fisher's Linear Discriminant Analysis (LDA) rather

than PCA. The primary purpose of LDA is to sepa-

Figure 3: BTG biceps and triceps signals on the first two

principal components.

rate samples of distinct groups by maximizing their

between-class separability while minimizing their

within-class variability.

Let the between-class scatter matrix

S be

defined as

∑

−−=

iiib

xxxxNS

))(( (2)

and the within-class scatter matrix

S be defined as

∑∑

−−=

iji

ijiw

xxxxS

)()( , (3)

where

is the m-dimensional pattern j from

class

N is the number of training patterns from

class

, and

is the total number of classes or

groups. The vector

x and matrix

S are

respectively the unbiased sample mean and sample

covariance matrix of class

(Fukunaga, 1990).

The grand mean vector

x is given by

∑∑∑

===

, (4)

where

N is the total number of samples, that is,

NNNN



The main objective of LDA is to find a

projection matrix

lda

that maximizes the ratio of the

determinant of the between-class scatter matrix to

the determinant of the within-class scatter matrix

(Fisher’s criterion), that is,

PSP

lda

maxarg=

(5)

However, the performance of the standard LDA

can be seriously degraded if there is only a limited

number of total training observations

N compared

to the dimension of the feature space m . Since the

A MULTIVARIATE STATISTICAL ANALYSIS OF MUSCULAR BIOPOTENTIAL FOR HUMAN ARM

MOVEMENT CHARACTERIZATION

229

within-class scatter matrix

is a function of

)( gN − or less linearly independent vectors, its

rank is

)( gN − or less. Therefore,

S is a singular

matrix if

N is less than )( gm + , or, analogously,

might be unstable if

N is not at least five to ten

times

)( gm + (Jain and Chandrasekaran, 1982).

To avoid the aforementioned critical issues of

the standard LDA in the limited sample and high

dimensional problem investigated here, we have

calculated

lda

by using a maximum uncertainty

LDA-based approach (MLDA) that considers the

issue of stabilising the

estimate with a multiple

of the identity matrix (Thomaz et al., 2004; Thomaz

and Gillies, 2005).

The maximum uncertainty LDA is constructed

by replacing

S with its regularization version in

the Fisher’s criterion formula described in equation

(5). A comprehensive description of this multivariate

statistical analysis method can be found in (Thomaz

and Gillies, 2005).

3 RESULTS

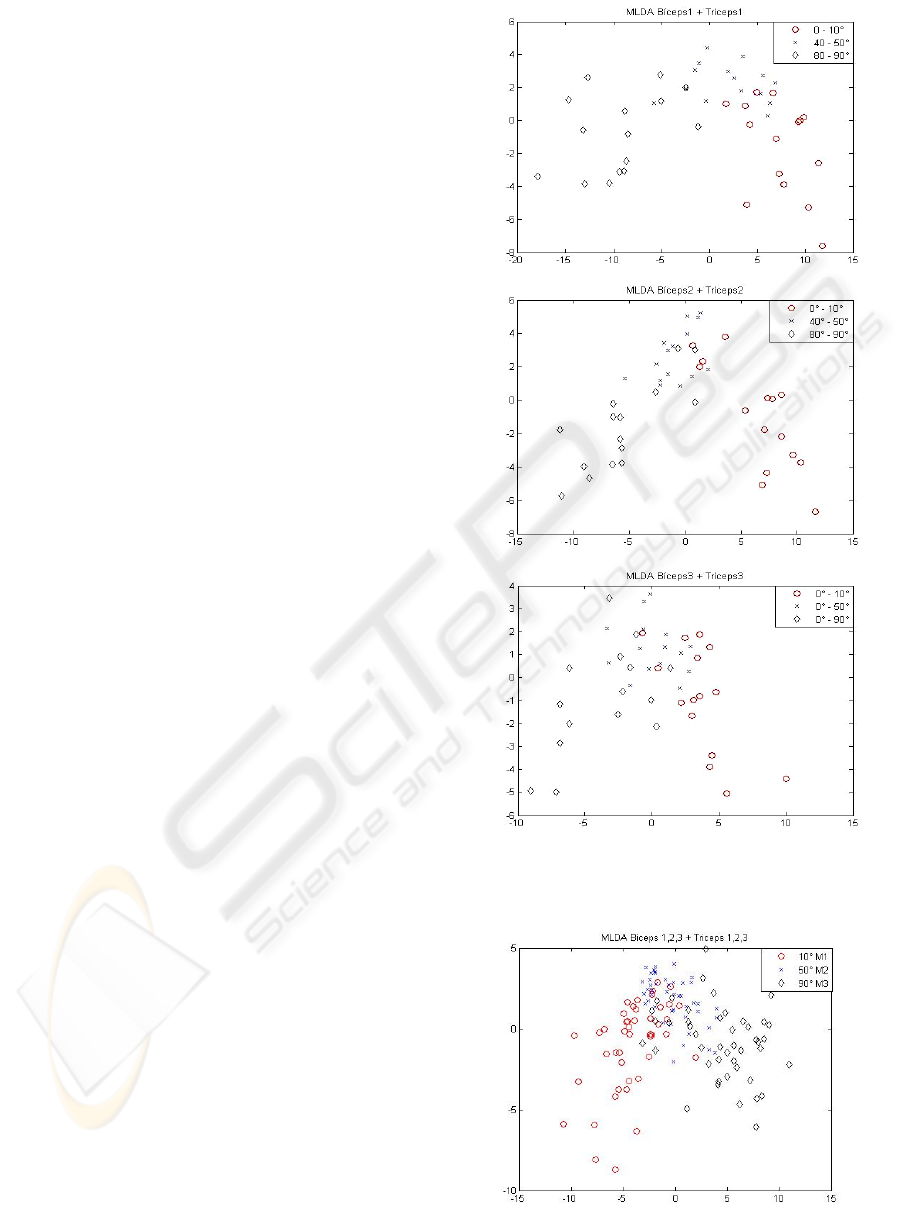
Figure 4 shows the PCA+MLDA transformation of

biceps and triceps signals treated together in tests 1,

2 and 3.

The two-stage PCA+MLDA multivariate linear

transformation reduces the dimensionality of the

original data and extracts the most discriminant

information from the patterns of interest. We have

retained all the PCA eigenvectors with non-zero

eigenvalues, that is,

1−

Nm , to reproduce the

total variability of the samples with no loss of

information.

BTG group was then analyzed, intending to

investigate the possibility of characterizing the

groups of movements based only on the executed

angular position instead of the muscle and the

related movement. Thus, by naming the classes with

the corresponding angular position and group labels

and considering three main groups as follows:

(M1) all the movements aiming 10º,

(M2) all the movements aiming 50º,

(M3) all the movements aiming 90º,

Figure 5 shows that even when analyzing the

different data set groups BT1, BT2 and BT3 on the

same 2D scatter plot it is still possible to see the 3

classes of data, which represent the final joint

position of the arm.

Figure 4: BT1 (top), BT2 (middle) and BT3 (bottom)

signals on the two PCA+MLDA most discriminant

components.

Figure 5: BTG biceps and triceps signals on the first two

PCA+MLDA most discriminant components.

BIOSIGNALS 2009 - International Conference on Bio-inspired Systems and Signal Processing

230

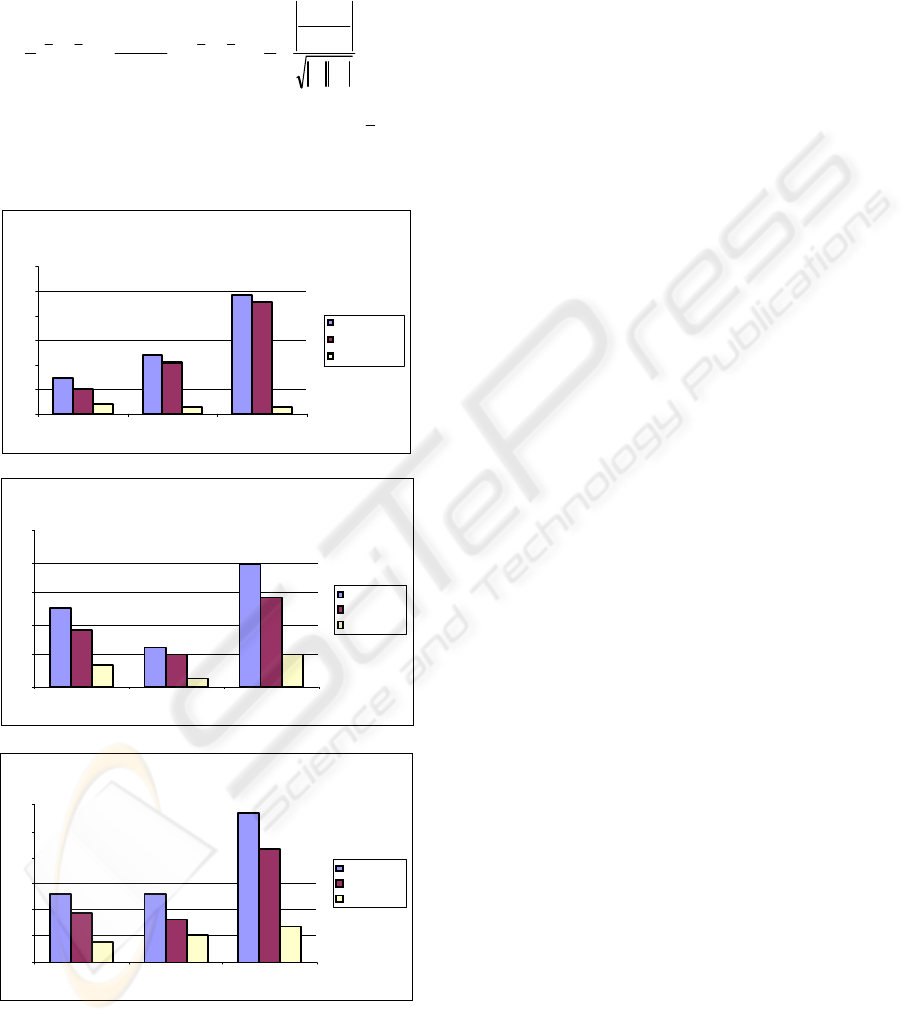
To quantify the PCA+MLDA linear separation

between the groups visually inspected in Figure 4,

we have used the Bhattacharyya distance (Fukunaga,

1990). The Bhattacharyya distance between two

groups of patterns can be defined as

(6)

where the notation “|.|” denotes the determinant of a

matrix. As described previously, the vector

x and

matrix

S are respectively the unbiased sample

mean and covariance matrix of class

(i = 1,2,3).

BT1 - Bhattacharyya Distance

0.5

1.5

2.5

M1 - M2 M2 - M3 M1 - M3

BT1 - MLDA d

BT1 - MLDA md

BT1 - MLDA cd

B T 2 - Bhatt acharyya D istance

0, 5

1, 5

2, 5

M1 - M2 M2 - M3 M1 - M3

BT2 - MLDA d

BT2 - MLDA md

BT2 - MLDA cd

B T 3 - Bhatt acharyya D istance

0, 2

0, 4

0, 6

0, 8

1, 2

M1 - M2 M2 - M3 M1 - M3

BT3 - MLD A d

BT3 - MLD A md

BT3 - MLD A cd

Figure 6: Quantification of the BTG biceps and triceps

signals separation on the PCA+MLDA linear

transformation using the Bhattacharyya distance.

Figure 6 illustrates the Bhattacharyya distance

calculated pairwisely between classes M1, M2 and

M3. For each group BT1 (top), BT2 (middle) and

BT3 (bottom), there is a measure of the total

Bhattacharyya distance (d), the Bhattacharyya

distance considering only its component related to

the mean differences (md), and the one related to

covariance differences (cd) only.

4 DISCUSSION

Initially, the acquired data was plotted in a

dispersion graph, as previously illustrated in Figure

2. As it can be seen, it was not possible to extract

any useful discriminant information from these

graphs because there was a lot of redundancy on it,

due to noise and the nature of the data itself. This

picture becomes more confused as the number of

samples increases.

To simplify and make possible this analysis, it was

used a two-stage linear transformation to reduce the

data set dimensionality and extract discriminant

information between the patterns of interest. First,

PCA was used making much easier the

understanding of the data group representation by

using a bi-dimensional space to represent the groups

of data on the first two principal components.

Afterwards, MLDA was used to improve the results

through the data discriminant analysis. Then, we

analyzed the biceps and triceps muscles to

investigate whether the signals could be roughly

separated. The signals provided by both muscles

could be linearly separated, as shown in Figure 3,

motivating the use of a combination of these signals

to discriminate the sets to determine the angular

joint arm position.

Figure 4 shows a clear separation of the studied

groups 0º-10º, 40º-50º and 80º-90º, which had been

very difficult to detect before using such two-stage

linear transformation. As it can be seen, there is a

little spot concentration in some points of the BT3

multivariate data analysis. This happens because, in

this case, the movement performed by the volunteers

started always at the same point, that is, 0º-10º, 0º-

50º and 0º-90º, and such experiment can make

harder to differentiate one movement from the other.

By applying all groups BT1, BT2 and BT3 in a new

bigger group BTG, whose aiming was to condense

the data and verify their class-separability, it was

still possible to determine the concentration regions

of the studied classes. However, there has been still

a slight overlap on these regions, as it was observed

on the separated groups BT1, BT2 and BT3.

)(

xxd

+−

⎟

⎠

⎞

⎜

⎝

⎛

−=

−

A MULTIVARIATE STATISTICAL ANALYSIS OF MUSCULAR BIOPOTENTIAL FOR HUMAN ARM

MOVEMENT CHARACTERIZATION

231

The Bhattacharyya distance was then calculated

to quantify the data group separation visually

inspected. The results on Figure 6 show that the

separation between groups M1 and M3 are bigger,

while the overlap is more evident between groups

M1- M2 and M2-M3. Therefore, as the movements

involved are more distant or different from each

other, more the set of signals become separated in its

own group or intra-class. This result was expected

but the experiment, especially with BTG group, has

showed the possibility of discriminating different

sets of data from different tests and obtaining a

reasonably understandable set of data, where classes

and groups could be linearly separated.

5 CONCLUSIONS

Our experimental results have suggested that

analyzing a given myoelectrical set of signals by

descriptive statistical tools is a hard task due to a

high data dimensionality and noise presence.

Acquiring myoelectrical signals with superficial

electrodes means to deal with a highly noisy

susceptible set of data due to electrical variances of

the skin and electrodes displacements during muscle

movements. The use of linear transformation can

make the multivariate data set analysis easier.

Considering the arm horizontal movement and

the acquired set of data used in this research, a

discriminant linear analysis showed that it is

possible not only to characterize the angular joint

position, but also to infer that different movements

recruit similar amounts of energy to be executed.

Our experimental results confirm that using

multivariate statistical analysis, myoelectric signal

recognition can be significantly improved after

linear transformations, which are practical and

feasible methods to analyze such multivariate high

dimension and small sample size data for further

classification.

ACKNOWLEDGEMENTS

The authors would like to thank the support

provided by the State of São Paulo Research

Foundation (FAPESP) under the grant 05/02899-4.

REFERENCES

Bittar, L. M. and Castro, M. C. F., 2008. Elbow Flexion

and Extension Movements Characterization by Means

of EMG. Biodevices 2008, Portugal, pp. 147-150.

Fukunaga, K., 1990. Introduction to statistical pattern

recognition, 2

edition. Academic Press, Boston.

Hargrove, L., Englehart, K. and Hudgins, B., 2008. A

training strategy to reduce classification degradation

due to electrode displacements in pattern recognition

based myoeletric control. Biomedical Signal

Processing and Control, 3(2), pp.175-180.

Henneberg, K., 2000. Principles of Electromyography. In:

Bronzino, J. D. (Eds.), The biomedical Engineering

Handbook, Vol. 1, 2

edition. CRC Press, New York.

cap. 14.

Jain, A. K. and Chandrasekaran, B., 1982, Dimensionality

and Sample Size Considerations in Pattern

Recognition Practice. In: Krishnaiah, P. R. and Kanal,

L. N. (Eds.), Handbook of Statistics, Vol. 2. North-

holland, Amsterdam. pp. 835-855.

Kleissen, R. F. M., Buurke, J. H., Harlaar, J., Zivold, G. ,

1998. Electromyography in the biomechanical analysis

of human movement and its clinical application. Gait

and Posture, 8(2), pp.143-158.

Thomaz, C. E. and Gillies, D. F., 2005. A Maximum

Uncertainty LDA-based approach for Limited Sample

Size problems - with application to Face Recognition.

In: Proceedings of SIBGRAPI’05, IEEE CS Press, pp.

89-96.

Thomaz, C. E., Gillies, D. F. and Feitosa, R. Q., 2004. A

New Covariance Estimate for Bayesian Classifiers in

Biometric Recognition, IEEE Trans. Circuits Syst.

Video Techn., 14(2), pp. 214-223.

BIOSIGNALS 2009 - International Conference on Bio-inspired Systems and Signal Processing

232