
TRANSFER FUNCTION OF THE HEART RATE CONTROL
SYSTEM WITH RESPIRATORY INPUT
The Classical Engineering Approach
Evgeny G. Vaschillo and Bronya Vaschillo
Center of Alcohol Studies, Rutgers, The State University of New Jersey, 607 Allison Road, Piscataway, NJ 08854, U.S.A.
Keywords: HR control system, Transfer function, Fourier filtration, HRV biofeedback, Resonance frequency.
Abstract: The classic “control system theory” approach was used to find the transfer function (TF) of the HR control
system with respiratory input. Eight healthy subjects, ages 19–40 participated in the study. Paced breathing
at seven frequencies in 0.5– 0.04 Hz range was used as sine-wave stimuli to assess the HR control system.
The sine-wave HR oscillation in response to each stimulus as the system’s output was recorded. Amplitude
and phase TFs were calculated for each frequency separately. The Fourier filtration procedure was used for
TF calculation. Experimentally obtained TFs revealed the same important features in all participants: 1) the
amplitude TF had its peak in a narrow frequency range around 0.1 Hz; 2) the phase TF successively
changed from positive to negative when breathing frequency increased, and passed “0” at frequency where
the amplitude TF peaked; 3) the peak frequency and magnitude were unique for each participant. These
features are evidence for the resonance property of the HR control system at a frequency around 0.1 Hz.
This study suggests that accurate identification of an individual’s resonance frequency can be found using
the TF features of HR control system and controlled breathing techniques.
1 INTRODUCTION
Respiratory activity continually perturbs the
cardiovascular system. Respiration modulates the
activity of most sympathetic and vagal efferents
through direct coupling between the respiratory and
autonomic centers and through modulation of central
sensitivity to baroreceptors and other afferent inputs
(Clynes, 1960; Saul et al., 1991). The autonomic
efferents, in turn, modulate peripheral vascular
resistance, heart rate (HR), and other autonomic
functions with respiratory periodicities. Thus,
respiration appears to actively participate in
autonomic and, in particular, HR regulation through
a very complex multiple-loops control system.
Respiration is a voluntary, controllable function and
thus can be exploited by researchers and clinicians
to develop novel approaches for correcting abnormal
autonomic regulation. For example, heart rate
variability (HRV) biofeedback can be used to
normalize autonomic regulation, increase baroreflex
gain and peak expiratory flow (Lehrer et al., 2003),
and treat asthma (Lehrer et al., 2004), major
depression (Karavidas et al., 2007), fibromyalgia
(Hassett et al., 2007), neurosis (Chernigovskaya et
al., 1990), and hypertension (McCrady et al., 2001).
Autonomic variability as well as the frequency
dependence of autonomic reactions to respiration are
critical factors in the development of such methods.
Accordingly, the classic engineering approach may
be useful in furthering our knowledge of this
system’s features.
The goal of this study is to assess the transfer
functions (TF) of the HR control system, using
breathing as the forcing function and heart rate as
the system response.
2 METHOD
The classic “control system theory” approach was
used to examine the transfer function of the HR
control system with respiration input. Sine-wave
stimuli of various frequencies were sent in-series to
the input of the system. The sine-wave HR
oscillation in response to each frequency stimulus
was recorded as the system’s output. Amplitude
(ratio of the amplitudes of the output and input sine-
wave signals) and phase (phase shift between the
233
G. Vaschillo E. and Vaschillo B. (2009).
TRANSFER FUNCTION OF THE HEART RATE CONTROL SYSTEM WITH RESPIRATORY INPUT - The Classical Engineering Approach.
In Proceedings of the International Conference on Bio-inspired Systems and Signal Processing, pages 233-238
DOI: 10.5220/0001434002330238
Copyright
c
SciTePress
sine-wave signals) transfer functions were calculated
separately for each frequency.
2.1 Participants and Procedure
Eight healthy subjects (5 males and 3 females), ages
19 – 40 (average 27.5) participated in the study. The
experimental session lasted one hour. Before the
session each participant was taught to breathe slowly
but not too deeply. A sine-wave pacer as well as the
participant’s current respiration curve were
presented on a computer screen. The participant was
instructed to follow the pacer with his/her breathing
such that his/her respiration curve precisely copied
the pacer’s amplitude and frequency. During the
experiment participants performed 7 paced breathing
tasks at 7 randomly presented frequencies (0.5,
0.25, 0.143, 0.11, 0.077, 0.055, and 0.04 Hz,
which corresponded to 30, 15, 5.6, 6.6, 4.6, 3.3,
and 2.4 breaths per minute). Each task included at
least 10 breaths and lasted for 3-5 minutes with 2
minutes break between them. The amplitude of the
pacer’s sine-wave curve was the same at all
frequencies and corresponded to approximately 1050
ml of tidal volume to provide relatively comfortable
breathing without hyperventilation.
2.2 Physiological Record
A J&J Engineering (Poulsbo, WA) I-330 DSP-12
physiograph was used to collect electrocardiogram
(ECG) and respiration data. ECG data were
collected from electrodes on the right arm and left
leg (Lead II), digitized at the rate of 1024 Hz. A
respiration strain gauge belt was attached around the
participant's chest. Respiration and pacer sine-wave
curves were digitized at the rate of 4 Hz.
Physiological data were collected during the whole
experiment and divided by tasks for data analysis.
2.3 Data Analysis
Beat-to-beat RR intervals (RRI) of the ECG signal
were measured and recalculated to heart rate [beats
per minute]. Cubic interpolation of the non-
equidistance HR sequence was completed, and the
HR curve was re-sampled at the rate of 4 Hz. The
TFs were calculated separately at each tested
frequency. The Fourier filtration algorithm (Eykhoff,
1974; Vaschillo et al., 2002) was applied for TF
calculation because it allowed more precise and easy
estimation of the amplitude and phase relation
between two sine-wave signals than cross-spectral
Fourier analysis. The algorithm was used to compute
two auxiliary TFs: (1) between the pacer as the input
and respiration as the output [TF(pr-resp)], and (2)
between the pacer as the input and HR as the output
[TF(pr-HR)]. This study targeted the TF of the HR
control system [TF(resp-HR)], which was calculated
by dividing TF(pr-HR) by TF(pr-resp), i.e. by
dividing the TF amplitudes and subtraction of the TF
phases.
3 RESULTS
The paced breathing exercise resulted in the sine-
wave oscillation in the participant’s HR paralleling
the sine-wave respiration curve. The amplitude and
phase relation between the pacer curve, respiration
curve, and sine-wave HR oscillation was strongly
dependent on pacer frequency.
3.1 Transfer Function of the Paced
Breathing
The TF(pr-resp) that reflects the participant’s ability
for precise pacer breathing is illustrated in Figure 1.
Participants were able to accurately maintain the
depth of breathing requested by the pacer, but
always preceded the pacer when asked to breathe at
a rate of less than 18 breaths per minute.
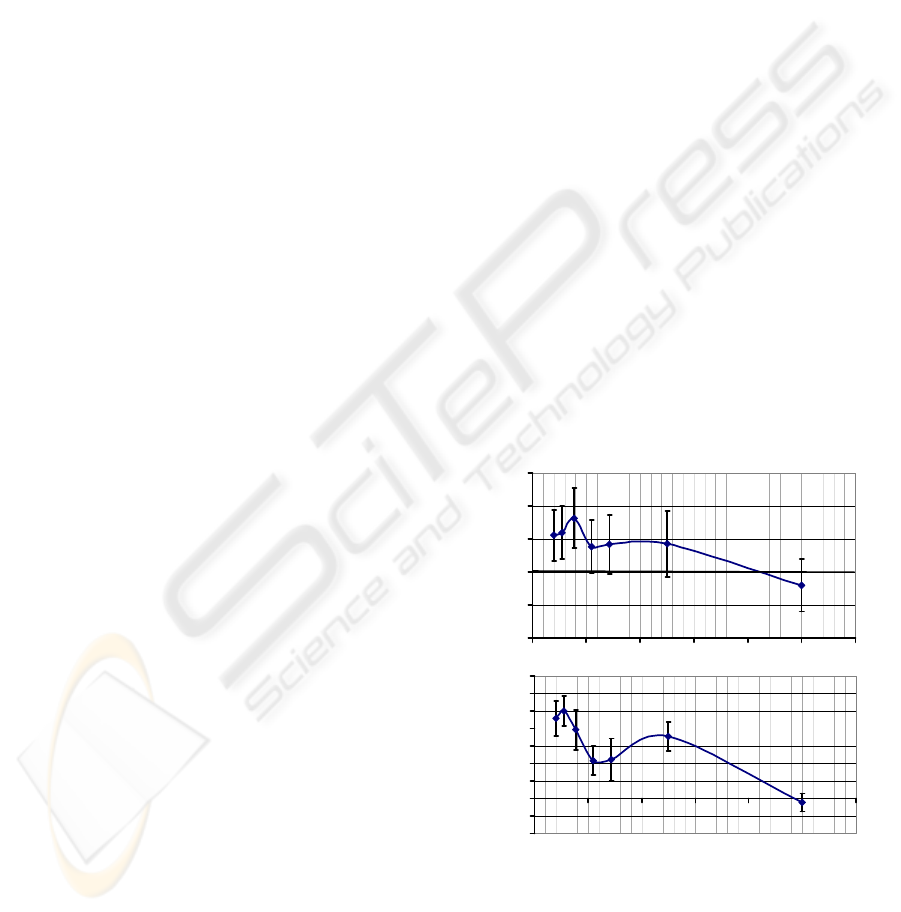
Figure 1: Transfer function of the paced breathing TF(pr-
resp) averaged across 8 participants: input – pacer, output
– respiration. Equality of the pacer and respiration curve
amplitudes correspond to value “1” of the amplitude
TF(pr-resp). Positive phase means that respiration
preceded the pacer.
0.9
0.95
1
1.05
1.1
1.15
0 0.1 0.2 0.3 0.4 0.5 0.6
Amplitude [arb]
-10
-5
0
5
10
15
20
25
30
35
0 0.1 0.2 0.3 0.4 0.5 0.6
Frequency [Hz]
Phase [degree]
BIOSIGNALS 2009 - International Conference on Bio-inspired Systems and Signal Processing
234
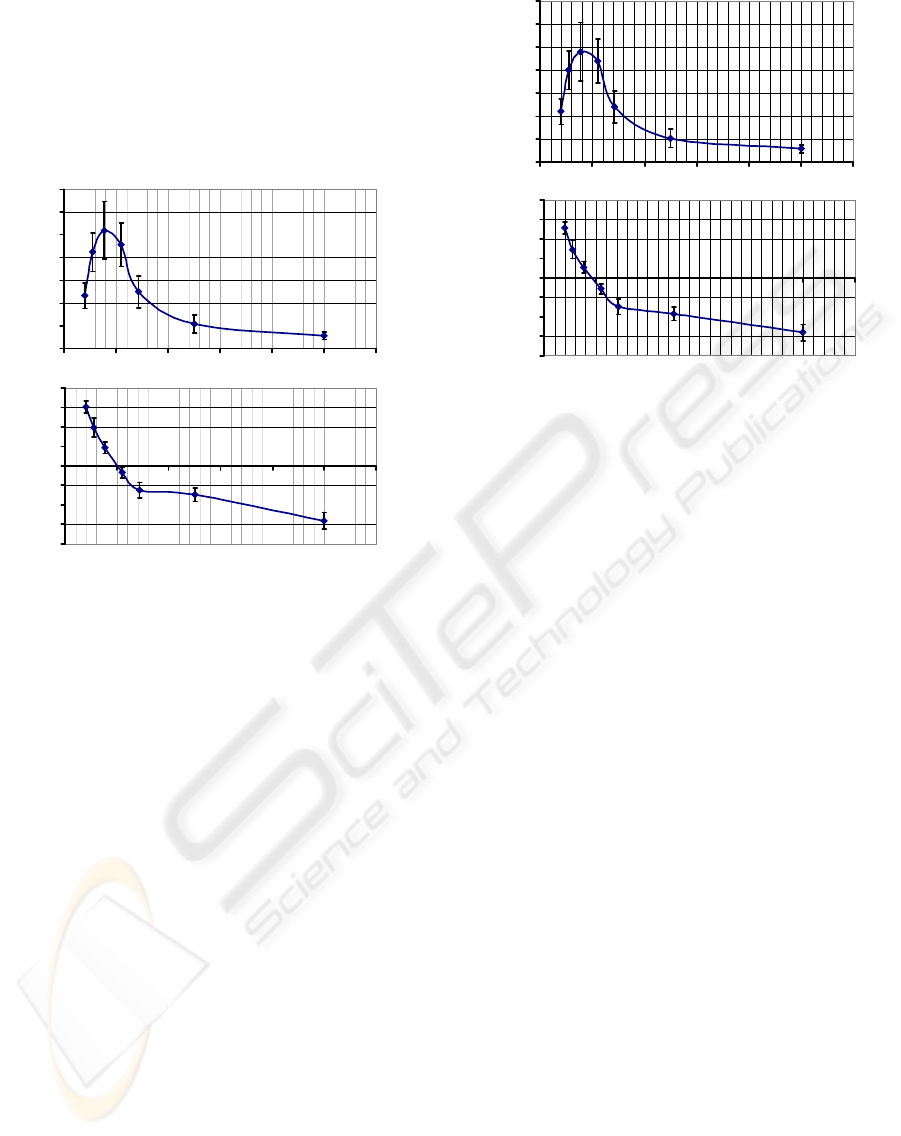
3.2 Transfer Function between the
Pacer and Heart Rate (Auxiliary)
Figure 2 presents the auxiliary TF(pr-HR), which
does not have any physiological meaning but is
necessary to calculate the targeted TF of the HR
control system in the Fourier filtration procedure.
Figure 2: Transfer function TF(pr-HR) averaged across 8
participants: input – pacer, output – heart rate.
3.3 Transfer Function of the Heart
Rate Control System
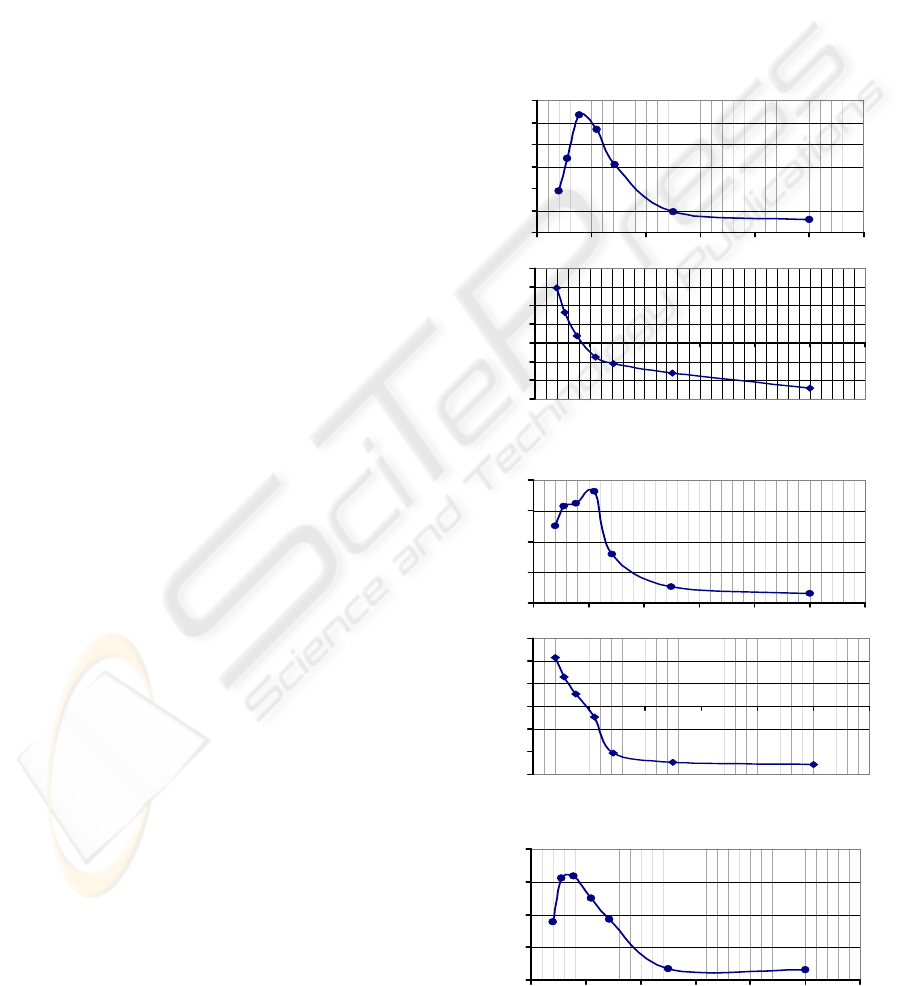
Figure 3 presents TF(resp-HR) and shows how
respiration affected HR. HR response to respiration
was strongest when participants were breathing at
frequencies around 0.1 Hz. Full synchronization of
sine-wave HR oscillation with respiration (phase TF
(resp-HR) is 0˚) occurred at only one frequency,
named as resonance frequency. At this frequency,
the amplitude of the TF(resp-HR) reached its
maximum. The HR curve preceded the respiration
curve at frequencies lower than the resonance
frequency and lagged behind the respiration curve at
frequencies higher than the resonance frequency.
Individual TF(resp-HR) graphs are presented in the
appendix; these figures show that the resonance
frequency and HR oscillation amplitude at resonance
frequency were unique for each participant.
Figure 3: Transfer function of the HR control system
TF(resp-HR) averaged across 8 participants: input –
respiration, and output – heart rate. The amplitude of the
TF(resp-HR) shows the amplitude of sine-wave HR
oscillation elicited by respiration at the corresponding
frequency. The zero phase of the TF(resp-HR)
corresponds to full synchronization of respiration with the
sine-wave HR oscillation; that is, HR goes up with
inhalation and down with exhalation.
4 DISCUSSION
The Amplitude and Phase Transfer Functions of the
HR control system [TF(resp-HR)] that were found in
this study reflect the relationship between respiration
and HR oscillation in 0.04-0.5 Hz frequency range.
As illustrated by the TF(resp-HR), the amplitude of
the respiration-dependent HR oscillations and the
phase between the HR oscillation and respiration
curves both depend on respiration frequency.
While the present amplitude TF findings are
consistent with the results of other studies (Angelone
and Coulter, 1963), (Cook et al., 1998), (Hirsch and
Bishop, 1981), (Saul et al., 1991), the phase TF
findings reported herein are only partially supported
by prior research. These results are in close
agreement with the sympathetically-controlled TFs
reported by Saul et al. (1991). However, they differ
from Angelone and Coulter (1963), who found that
respiration and HR oscillation were in phase at
frequencies lower than 0.05 Hz and, that at ~0.1 Hz,
the phase angle was about -90º. They also differ
from Eckberg (1983) who reported the 0º phase
between respiration and HR oscillation occurred at
the ~0.2 Hz frequency.
-200
-150
-100
-50
0
50
100
150
200
0 0.1 0.2 0.3 0.4 0.5 0.6
Frequency [Hz]
Phase [degree]
-200
-150
-100
-50
0
50
100
150
200
0 0.1 0.2 0.3 0.4 0.5 0.6
Frequency [Hz]
Phase [degree]
0
0.05
0.1
0.15
0.2
0.25
0.3
0.35
0 0.1 0.2 0.3 0.4 0.5 0.6
Ampitude [arb]
0
0.05
0.1
0.15
0.2
0.25
0.3
0.35
0 0.1 0.2 0.3 0.4 0.5 0.6
Amplitude [arb]
TRANSFER FUNCTION OF THE HEART RATE CONTROL SYSTEM WITH RESPIRATORY INPUT - The Classical
Engineering Approach
235

These discrepancies can be explained in part by
the findings of Saul et al. (1991) who noted a
dramatic difference between the TF(resp-HR) that is
only under sympathetic control (parasympathetic
blockade) and the TF that is under vagal control.
Indeed, most prior studies, including Angelone and
Coulter (1963) and Eckberg (1983), did not control
sympathetic and vagal activity in their studies. In the
present study, the paced breathing procedure was
challenging enough to activate sympathetic and
depress parasympathetic systems. Moreover,
discrepancies may exist due to the use of cross-
spectral Fourier analysis in these earlier studies,
which may not have provided accurate phase
estimation. The present study used more precise
Fourier filtration procedures to estimate phase
relations, and was thus able to obtain individual TFs
that were stable for all participants.
The TF(resp-HR)s reported in our study
consistently demonstrated that: 1) the amplitude TF
has its peak in a narrow frequency range around 0.1
Hz; 2) the phase TF successively changed from
positive to negative when breathing frequency
increased, and passed “0º” at same frequency where
the amplitude TF peaked; 3) the frequency and
magnitude of the peak were unique for each
participant. These findings lend support for the
identification of the resonance property of the HR
control system at a frequency of approximately 0.1
Hz.
It is known that HR baroreflex closed-loop
provides the ~0.1 Hz resonance properties in the HR
control system (Cevese et al., 2001), (Vaschillo,
Vaschillo, & Lehrer, 2006). Earlier studies showed
that HR resonance can be triggered not only by
respiration, but by other rhythmical stimuli, such as
rhythmical emotional stimulation (Vaschillo et al.,
2008) or rhythmical muscle tension (Vaschillo et al.,
2007). This suggests that the resonance property of
the HR control system does not depend on
respiration and the TF(resp-HR) reflects properties
of the HR baroreflex.
The studies also revealed that the ~0.1 Hz
resonance oscillation in HR usually is accompanied
by the same frequency high amplitude oscillation in
other cardiovascular functions (e.g., in arterial blood
pressure and in vessel tone (
Cooke et al., 1998; Lehrer
et al., 2003, 2004).
HRV biofeedback is used to train participants to
control breathing such that they can harness the 0.1
Hz resonance in the cardiovascular system. The
therapeutic effects of HRV biofeedback occur as the
result of generalized high-amplitude oscillations in
autonomic functions elicited by the biofeedback
procedure (Chernigovskaya et al., 1990; Lehrer et
al., 2003, 2004). These oscillations train autonomic
reflexes, and systematic training of autonomic
reflexes normalizes and improves autonomic
regulation. To maximize oscillations and,
accordingly, the therapeutic effects of biofeedback,
the patient’s precise resonance frequency should be
determined; however this historically has been
difficult to assess (Vaschillo, et al., 2002, 2006).
This study suggests that knowledge of the TF(resp-
HR) features and the use of controlled breathing
techniques may allow more accurate identification
of an individual’s resonance frequency.
5 CONCLUSIONS
Classical control system theory applied to the
investigation of physiological systems can be a
useful tool for the medical practice. Physiological
systems function via closed-loop reflexes within a
very narrow frequency range, thereby suggesting
that application of sine-wave stimuli with Fourier
filtration procedure may be more effective for
testing such systems than multi-frequency stimuli
with the cross-spectral Fourier analysis.
ACKNOWLEDGEMENTS
This research was supported by grants from the
National Institute of Alcohol Abuse and Alcoholism
(R01 AA015248 and K02 AA00325) and the
National Institute of Drug Abuse (P20 DA017552).
REFERENCES
Angelone, A., & Coulter, N. A. Jr., 1964. Respiratory
sinus arrhythmia: A frequency depended phenomenon.
Journal of Applied Physiology, 19, 479–82.
Chernigovskaya, N. V., Vaschillo, E. G., Rusanovsky, B.
B., & Kashkarova, O. E., 1990. Instrumental
autotraining of mechanisms for cardiovascular
function regulation in treatment of neurotics. The SS
Korsakov's Journal of Neuropathology and
Psychiatry, 90, 24–28.
Cevese A, Gulli G, Polati E, Gottin L, Grasso R. 2001.
Baroreflex and oscillation of heart period at 0.1 Hz
studied by alpha-blockade and cross-spectral analysis
in healthy humans. The Journal of Physiology. 15;
531(Pt1); 235-244.
Clynes, M., 1960. Respiratory sinus arrhythmia: laws
derived from computer simulation. Journal of Applied
Physiology,15(5): 863-874.
BIOSIGNALS 2009 - International Conference on Bio-inspired Systems and Signal Processing
236
Cooke, W. H., Cox, J. F., Diedrich, A. M., Taylor, J. A.,
Beightol, L. A., Ames, J. E. 4th, Hoag, J. B., Seidel,
H., & Eckberg, D. L., 1998. Controlled breathing
protocols probe human autonomic cardiovascular
rhythms. American Journal of Physiology, 274(2 Pt 2),
H709–18.
Eckberg, D.L., 1983. Human sinus arrhythmia as an index
of vagal cardiac outflow. Journal of Applied
Physiology, 54, 961-966.
Eykhoff P., 1974. The book, System identification:
parameter and state estimation. Chichester, England:.
Wiley, 555 p.
Hassett, A.L, Radvanski, D.C., Vaschillo, E., Vaschillo,
B., Sigal, L., Karavidas, M., Buyske, S., Lehrer, P.M.,
2007. A pilot study of the efficacy of heart rate
variability biofeedback in patients with fibromyalgia
syndrome. Applied Psychophysiology and
Biofeedback, 32(1): 1-10.
Hirsh, J.N., and Bishop, B., 1981. Respiratory sinus
arrhythmia in humans:how breathing pattern
modulates heart rate. American Jurnal of Physiology,
241(10): 620-629.
Karavidas, M.K., Lehrer, P.M., Vaschillo, E., Vaschillo,
B., Marin, H., Buyske, S., Radvanski, D., Hasset, A.,
2007. Preliminary results of an open label study of
heart rate variability for the treatment of major
depression. Applied Psychophysiology and
Biofeedback, 32(1): 19-30.
Lehrer, P. M., Vaschillo, E., Vaschillo, B., Lu, S. E.,
Eckberg, D. L., Edelberg, R., Shih, W. J., Lin, Y.,
Kuusela, T. A., Tahvanainen, K. U. O., & Hamer, R.,
2003. Heart rate variability biofeedback increases
baroreflex gain and peak expiratory flow.
Psychosomatic Medicine, 65, 796–805.
Lehrer, P., Vaschillo, E., Vaschillo, B., Lu, S., Scardella,
A., Siddique, M., & Habib, R., 2004. Biofeedback
treatment for asthma. Chest, 126, 352–361.
McCraty, R., Atkinson, M., & Tomasino, D., 2003. Impact
of a workplace stress reduction program on blood
pressure and emotional health in hypertensive
employees. The Journal of Complementary and
Alternative Medicine, 9, 355–369.
Saul, J. P., Berger, R. D., Albrecht, P., Stein, S. P., Chen,
M. H., Cohen, R. J., 1991. Transfer function analysis
of the circulation: unique insights into cardiovascular
regulation. American Journal of Physiology, 261(4 Pt
2), H1231–1245.
Vaschillo, E.G., Bates, M.E., Vaschillo, B., Lehrer, P.,
Udo, T., Mun, E.Y., & Ray, S., 2008. Heart rate
variability response to alcohol, placebo, and emotional
picture cue challenges: Effects of 0.1 Hz stimulation.
Psychophysiology, 45(5), 847-858.
Vaschillo, E., Vaschillo, B., Bates, M.E., Lehrer, P.,
France, Ch., & Trost, Z. Rhythmical muscle tension
mimics heart rate variability biofeedback. 2007.
Applied Psychophysiology and Biofeedback. 32(2),
132-133.
Vaschillo, E., Vaschillo, B., & Lehrer, P., 2006.
Characteristics of resonance in heart variability
stimulated by biofeedback. Applied Psychophysiology
and Biofeedback, 31(2, 129-142
.
Vaschillo, E., Lehrer, P., Rishe, N., & Konstantinov, M.,
2002. Heart rate variability biofeedback as a method
for assessing baroreflex function: a preliminary study
of resonance in the cardiovascular system. Applied
Psychophysiology and Biofeedback, 27, 1–27.
APPENDIX
Individual Transfer Functions for 8
Participants
Participant A
Participant B
Participant C
0
0.05
0.1
0.15
0.2
0.25
0.3
0 0.1 0.2 0.3 0.4 0.5 0.6
Amplitude
-150
-100
-50
0
50
100
150
200
0 0.1 0.2 0.3 0.4 0.5 0.6
Frequency (Hz)
Phase (Degree)
0
0.05
0.1
0.15
0.2
0 0.1 0.2 0.3 0.4 0.5 0.6
Ampliyude
-150
-100
-50
0
50
100
150
0 0.1 0.2 0.3 0.4 0.5 0.6
Phase (Degree)
0
0.05
0.1
0.15
0.2
0 0.1 0.2 0.3 0.4 0.5 0.6
Amplitude
TRANSFER FUNCTION OF THE HEART RATE CONTROL SYSTEM WITH RESPIRATORY INPUT - The Classical
Engineering Approach
237
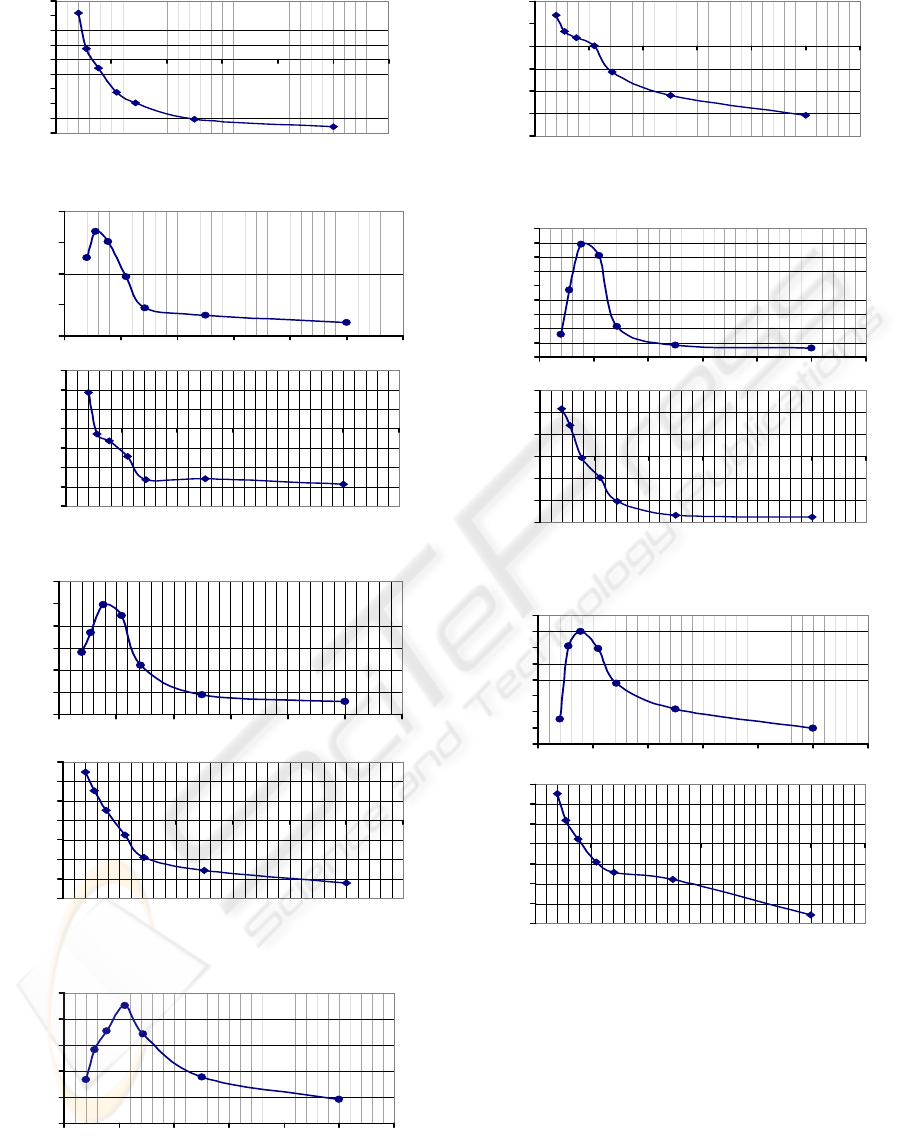
Participant D
Participant E
Participant F
Participant G
Participant H
-100
-80
-60
-40
-20
0
20
40
60
80
0 0.1 0.2 0.3 0.4 0.5 0.6
Phasa (Degree)
0
0.05
0.1
0.15
0.2
0 0.1 0.2 0.3 0.4 0.5 0.6
Amplitude
-200
-150
-100
-50
0
50
100
150
0 0.1 0.2 0.3 0.4 0.5 0.6
Phase (Degree)
0
0.05
0.1
0.15
0.2
0.25
0.3
0 0.1 0.2 0.3 0.4 0.5 0.6
Amplitude
-200
-150
-100
-50
0
50
100
150
0 0.1 0.2 0.3 0.4 0.5 0.6
Phase (Degree)
0
0.05
0.1
0.15
0.2
0.25
0 0.1 0.2 0.3 0.4 0.5 0.6
Amplitude
0
0.05
0.1
0.15
0.2
0.25
0.3
0.35
0.4
0.45
0 0.1 0.2 0.3 0.4 0.5 0.6
Amplitude
-150
-100
-50
0
50
100
150
0 0.1 0.2 0.3 0.4 0.5 0.6
Phase (Degree)
0
0.05
0.1
0.15
0.2
0.25
0.3
0.35
0.4
0 0.1 0.2 0.3 0.4 0.5 0.6
Amplitude
-200
-150
-100
-50
0
50
100
150
0 0.1 0.2 0.3 0.4 0.5 0.6
Phase (Degree)
-200
-150
-100
-50
0
50
100
0 0.1 0.2 0.3 0.4 0.5 0.6
Phase (Degree)
BIOSIGNALS 2009 - International Conference on Bio-inspired Systems and Signal Processing
238
