
CMB ANISOTROPIES INTERPOLATION
Svitlana Zinger
1
, Jacques Delabrouille
2
, Michel Roux
3
and Henri Maˆıtre
3
1
Eindhoven University of Technology, P.O. Box 513, 5600 MB Eindhoven, Netherlands
2
CNRS, Laboratoire APC, 10 rue Alice Domon et L´eonie Duquet, 75205 Paris Cedex 13, France
3
Ecole Nationale Sup´erieure des T´el´ecommunications, 46 rue Barrault, 75634 Paris Cedex 13, France
Keywords:
Interpolation, Cosmic Microwave Background, Binning, Kriging.
Abstract:
We consider the problem of the interpolation of irregularly spaced spatial data, applied to observation of
Cosmic Microwave Background (CMB) anisotropies.The well-known interpolation methods and kriging are
compared to the binning method which serves as a reference approach. We analyse kriging versus binning
results for different resolutions and noise level in the original data. Most of the time, kriging outperforms the
other methods for producing a regularly gridded, minimum variance CMB map.
1 INTRODUCTION
In this article we consider the problem of the inter-
polation of a set of data points for mapping Cosmic
Microwave Background (CMB) anisotropies.
CMB is a relic radiation emitted when the Uni-
verse was about 380,000 years old. Almost homo-
geneous and isotropic, it has small brightness irreg-
ularities of the order of one part per 100000, which
are imprinted by the tiny inhomogeneities which will
give rise to the large scale structures observable in the
Universe today, about 12 billion years later (Barreiro,
2000).
The observation of these anisotropies permits to
constrain the possible scenarios for describing the
content and evolution of our Universe. Many exper-
iments dedicated to these measurements have been
conducted in the past 20 years, included two space
missions and many ballon-borne or ground-based ex-
periments. ESA is planning launch the Planck space-
craft, for yet another space mission for observing
these signals with unprecedented accuracy. The scan-
ning strategy, which defines the scanning pattern on
the sky, is set by external constraints, which results in
general in somewhat irregularly gridded observations.
For this paper, we will investigate the problem of
interpolation on synthetic data sets which features a
few of the main difficulties encountered in real CMB
experiments.
2 DATA DESCRIPTION
The “data” used in this work is a simulated data set
covering a portion of the sky small enough to be
approximated by a tangent plane. The astrophysi-
cal signal comprises a 2-dimensional random field
∆T
T
(~n) ≡
T(~n)−T
0
T
0
, where ~n is a unit vector on the
sphere. In addition, the map comprises emission from
about a thousand point sources, one of which is strong
enough to be representative of a bright planet. The
original sky map is convolved with a gaussian ker-
nel, to simulate the effect of the finite resolution of
the experiment. The original sky map is “observed”
in a number of points, arranged on fractions of circu-
lar scans. This is representative of the scanning of a
typical CMB instrument as Archeops. The real mea-
surements of CMB experiments are affected by noise.
This is modelled by adding a Gaussian noise with the
standard deviation in the range 0.2 to 1, so that the
SNR of measurements is typically between unity and
a few (units are arbitrary in the simulation). Although
the real cosmological measurements are made on a
sphere and therefore are determined using angles, we
consider local Cartesian coordinates. The simulated
measurements are the x,y coordinates and the corre-
sponding anisotropy. Figure 1 shows x coordinates
plotted versus y coordinates of the data. From this
plot one can see the lines formed by the scanning pat-
tern. The total amount of points is 47914, 13 of them
correspond to the large point source in the data.
155
Zinger S., Delabrouille J., Roux M. and Maître H. (2009).
CMB ANISOTROPIES INTERPOLATION.
In Proceedings of the First International Conference on Computer Imaging Theory and Applications, pages 155-158
DOI: 10.5220/0001434401550158
Copyright
c
SciTePress

50 100 150 200 250 300 350 400 450 500
50
100
150
200
250
300
350
400
450
500
Figure 1: Simulated CMB measurements: x coordinates
versus y coordinates.
3 INTERPOLATION METHODS
We now present the interpolation experiments using
the simulated CMB data described above, with the
objective to identify the method best suited for resam-
pling the CMB data on a regular grid.
We specifically address the following problem.
For x and y coordinates varying between 0 and 511,
make an image with the size 128 × 128, 256 × 256
and 512× 512. This task considers the complete zone,
with low density of measures in some regions. This
task should also be performed on the data with noise.
We investigate several techniques that may be
used for the CMB measurements interpolation. We
consider triangle-based linear interpolation, kriging
and binning. Among those, we would like to choose
the best interpolation method according the root mean
square error (RMSE).
Binning, which simply consists in averaging mea-
surements “falling” in bins, is very simple and fast. It
is traditionally used for CMB observations.
Triangle-based interpolation is a method which
estimates the value of the observation at each sam-
pling point using the Delaunay triangulation, as a lin-
ear combination of data values at the vertices of the
appropriate triangle.
Kriging is similar to spline interpolation (Billings
et al., 2002) that can be presented as an energy min-
imization problem (Wolberg and Alfy, 2002). The
disadvantage of the cost function minimization is
the use of the coefficient for the regularization term.
The change of this coefficient will change the results
(Zinger et al., 2002).
The advantage of kriging over energy minimiza-
tion is that the parameters for kriging are obtained by
the analysis of the experimental variogram, that is ob-
tained from the original data, while the coefficient for
the regularization term in the energy expression is the
parameter to tune.
3.1 Linear Interpolation
Linear interpolation is based on Delaunay triangula-
tion of the original data. Triangle-based linear inter-
polation applies barycentric coordinates to the data at
the vertices of the triangle (Watson, 1992). Triangle-
based linear interpolation does not give good results
on the noisy data (Figure 2).
Figure 2: Triangle-based interpolation, x and y vary be-
tween 0 and 511, pixel size is 4 units.
3.2 Kriging
Kriging considers measurements as samples from a
realization of a stationary random process and analy-
ses the spatial behaviour of the corresponding param-
eters. The interpolation in this case consists of mak-
ing a weighted sum of the data points. The weights
are calulated using the variogram - a function that ex-
presses the spatial dependency between data. Most of
the research on the nature of the CMB anisotropies
characterizes them as a stationary random process of
the second order. Therefore the assumptions for krig-
ing (Cressie, 1991) are well verified for the CMB
data. Before using kriging it is necessary to determine
the three parameters of the variogram: the nugget, the
sill and the range (Billings et al., 2002). So the experi-
mental variogram is calculated, then these parametera
are obtained, and the used in the formula of the theo-
retical variogram.
We perform the kriging interpolation on neighbor-
hoods of size 10 by 10 units. Kriging on a fixed neigh-
borhood allows quick performance on large data sets
- it is an advantage for a real data interpolation.
The parameters estimated for the theoretical vari-
ogram from the noisy data are: range is 43, nugget is
1, sill is 1.8. An example of a resulting image is in
Figure 3.
IMAGAPP 2009 - International Conference on Imaging Theory and Applications
156

resolution is 4 units
Kriging: range is 43, nugget is 1, sill is 1.8
20 40 60 80 100 120
20
40
60
80
100
120
−2
−1
0
1
2
3
4
5
6
Figure 3: Kriging, x and y vary between 0 and 511, pixel
size is 4 units.
From the kriging results it is evident that the algo-
rithm suppresses noise.
3.3 Binning
A common and simple approach, that is often used in
astronomy, is binning. The method consists of aver-
aging the data values inside each bin centered around
a pixel to be computed. After having found the data
points located inside the area of a bin, the average of
these points values is attributed to the pixel. If there
are no data points inside a bin, then this pixel stays
empty, no value is assigned to it. If the bin size is
taken to be 2 units, then much less points fall inside
pixels. And when the bin size is 1 unit, then more than
80% of the pixels are empty and the pixels that have
data points, assigned to them, have just one point. So
in this case averaging is not possible. Figure 4 shows
results of binning.
resolution is 4 units
Binning on the noisy simulated CMB data
20 40 60 80 100 120
20
40
60
80
100
120
empty pixel
0
5
10
Figure 4: Binning, the resolution is 4 units.
4 COMPARISONS WITH THE
REFERENCE
Since our data is simulated, we can have a refer-
ence image to estimate the quality of the interpola-
tion methods. The root mean square errors (RMSE)
between the reference and interpolation results are in
Table 1.
Table 1: RMSE between the reference and the interpolation
results, x and y coordinates vary between 0 and 512.
Interpolation method Resolution
1 unit 2 units 4 units
Binning 0.9836 0.9238 0.6827
Linear 0.7152 0.7146 0.7085
Kriging 0.2930 0.2928 0.2900
From the RMSE values it is clear that kriging
gives better results than the other two interpolation
methods. The performance of binning becomes better
if the size of the pixel increases, since the larger the
bin, the more data points inside it. It is even possible
that binning gives better results than other methods
when the bin size is larger (and therefore, the resolu-
tion lower). Kriging has an advantage over binning,
because of using weighted average of the data and be-
cause the weights depend on the data statistics.
The quality of binning obviously depends on the
density of data points per regular grid pixel. Figure 5
demonstrates it.
0 5 10 15 20 25 30
0
0.2
0.4
0.6
0.8
1
1.2
1.4
Amount of points that fall inside a pixel
RMSE between the reference and binning result
Experiments on the data with noise, pixel size is 4x4
KRIGING
Figure 5: Hit counts versus RMSE for binning interpola-
tion. The horizontal line represents the RMSE value for
kriging with the same pixel size on the same data.
We can see that averaging on 10 or more pixels
often leads to the smaller errors than the ones of krig-
ing. So binning can outperform kriging only when the
density of points is quite high.
CMB ANISOTROPIES INTERPOLATION
157
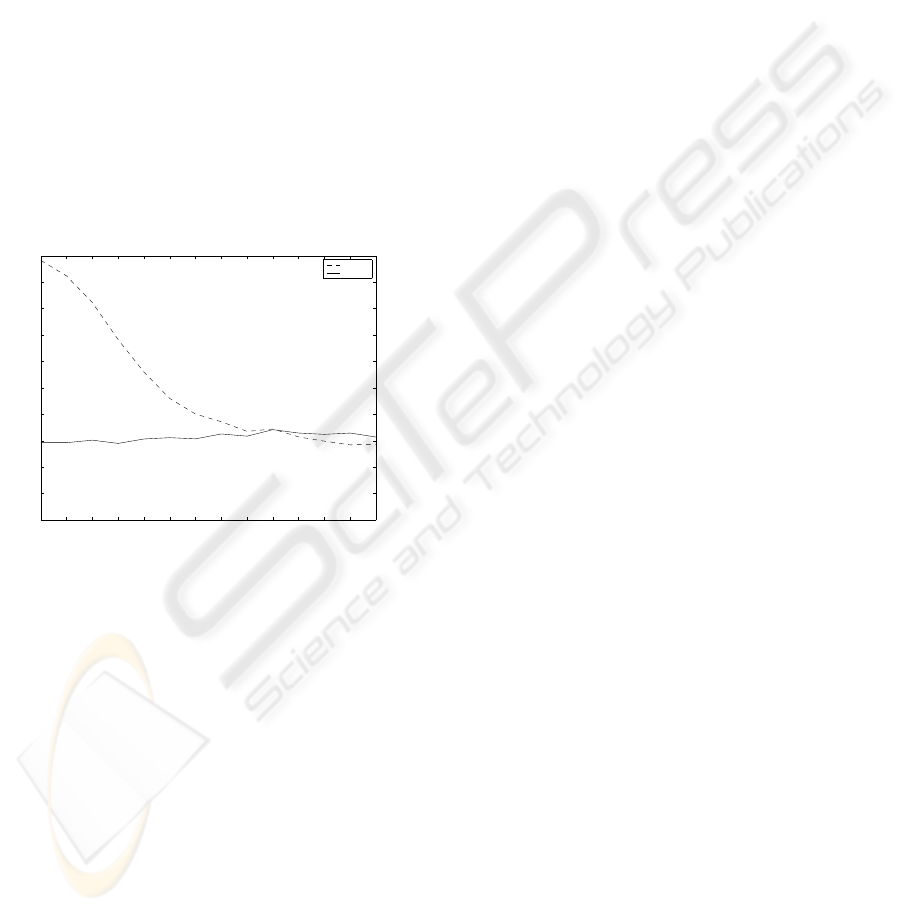
5 KRIGING VERSUS BINNING:
PERFORMANCE ANALYSIS
From the previous results it is obvious that kriging
outperforms several other methods that we tried. The
reference method - binning - works worse especially
in the cases of small grid sizes, i.e. high resolution.
From the experiments presented above we can see
that kriging is the best, but binning can improve its
performance if the size of the pixel is enlarged, pos-
sibly at the price of reduced map resolution. When
the standard deviation of noise is 1, it is the case for
the Archeops acquisition system. We vary the pixel
size in order to see how it influences the interpolation
results.
Figure 6 demonstrate the RMSE measured be-
tween the reference and kriging or binning interpola-
tion results for different sizes of the pixel. Solid line
represent kriging, dashed - binning.
1 2 3 4 5 6 7 8 9 10 11 12 13 14
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
RMSE between the reference and the interpolation result
grid size
standard deviation for the noise is 1
binning
kriging
Figure 6: Kriging versus binning performance, standard de-
viation of noise is 1.
It is easy to see that the larger is the size of pixel,
the better is the binning result. The important advan-
tage of kriging is that its performance does not depend
on the choice of the resolution for the image. The
stronger is the noise, the larger pixel size is needed
in order to get binning results as good as the ones of
kriging. The grid size is 10 units when both methods
start having the same performance in the presence of
strong noise.
From the practical point of view, the size of the
grid equal to 7 or to 10 units is much too coarse. If
one wants to have the size of the grid the same as the
average density of the original scattered CMB data,
then it should be approximately 3 units.
6 CONCLUSIONS
Several methods can be used for the interpolation of
CMB anisotropies observations. These measurements
are irregularly distributed 3D points. In practice, they
are affected by noise and by other radiation sources.
We have considered the simulated data, composed by
the CMB anisotropiesand point sources and the noise.
For the data with noise we tried linear interpola-
tion, kriging and binning. Adding the noise compli-
cates the problem, especially because the range of the
noise is almost as large as the range of the data. In
this case an interpolation technique should be able
to decrease the effect of noise as much as possible.
The best results are obtained with the kriging tech-
nique, because it allows to take the noise into account
through the parameters of the variogram.
Binning is often used in astronomy, it averages the
values of the data inside each pixel and so can de-
crease the noise. The disadvantage is that the density
of data points should be at least ten times higher than
the density of the regular grid in order to get good re-
sults. It is also desirable for binning to have evenly
distributed data points. Taking binning as the ref-
erence method, we make a detailed comparison be-
tween this method and kriging. We find that these
two methods can be equally good when the regular
grid size of the image to find is very coarse. Oth-
erwise, for acceptable grid sizes kriging outperforms
binning.
REFERENCES
Barreiro, R. B. (2000). The cosmic microwave background:
state of the art. New Astronomy Reviews, 44:179–204.
Billings, S. D., Beatson, R. K., and Newsam, G. N. (2002).
Interpolation of geophysical data using continuous
global surfaces. Geophysics, 67(6):1810–1822.
Cressie, N. A. (1991). Statistics for spatial data. A Wiley-
Interscience publication.
Watson, D. F. (1992). Contouring: a guide to the analysis
and display of spatial data. Pergamon Press.
Wolberg, G. and Alfy, I. (2002). An energy minimization
framework for monotonic cubic spline interpolation.
Journal of Computational and Applied Mathematics,
143(2):145–188.
Zinger, S., Nikolova, M., Roux, M., and Maˆıtre, H. (2002).
3d resampling for airborne laser data of urban areas.
In Proc. ISPRS Symposium PCV’02, volume XXXIV,
pages 418–423.
IMAGAPP 2009 - International Conference on Imaging Theory and Applications
158
