
AGENT-BASED SIMULATION OF SOCIAL LEARNING
IN CRIMINOLOGY
Tibor Bosse, Charlotte Gerritsen and Michel C. A. Klein
Vrije Universiteit Amsterdam, Department of Artificial Intelligence
de Boelelaan 1081a, 1081 HV Amsterdam, The Netherlands
Keywords: Agent-based simulation, Social learning, Delinquent behaviour.
Abstract: Criminal behaviour exists in many variations, each with its own cause. A large group of offenders only
shows criminal behaviour during adolescence. This kind of behaviour is largely influenced by the
interaction with others, through social learning. This paper contributes a dynamical agent-based approach to
simulate social learning of adolescence-limited criminal behaviour, illustrated for a small school class. The
model is designed in such a way that it can be compared with data resulting from a large scale empirical
study.
1 INTRODUCTION
Within Criminology, the analysis of the emergence
of criminal behaviour is one of the main challenges
(Gottfredson and Hirschi, 1990). An important
mechanism behind the emergence of criminal
behaviour is social learning (Burgess and Akers,
1966). To analyse this mechanism, this paper
presents an agent-based approach to simulate social
learning, which specifically addresses the mutual
influence of peers, parents and school, with respect
to delinquent behaviour.
To formalise and analyse the emergence of
criminal behaviour through social learning, an
artificial society has been modelled to represent a
small school class. The models for the agents have
been formally specified by executable
temporal/causal logical relationships, using the
modelling language TTL (Bosse et al., 2006) and its
executable sublanguage LEADSTO (Bosse et al,
2007). This language allows the modeller to
integrate both qualitative, logical aspects as
quantitative, numerical aspects. Moreover, since the
language has a formal logical semantics, simulation
models created in TTL and LEADSTO can be
formally analysed by means of logical analysis
techniques.
In the field of Criminology, it is often quite
difficult to perform experiments that involve
changes in the real world. A model as the one
presented in this paper can be used to study general
patterns in the development of criminal behaviour.
Simulation can help to answer what-if questions and
to verify theories about the relation between
different processes. Discussions with a team of
criminologists taught us that the evidence provided
by simulation models is already considered as useful
knowledge about the relevance of criminological
theories such as the differential association theory,
which will be discussed below.
In a next step of the research, we plan to validate
the model using data of an existing empirical study
e.g. (Weerman and Bijleveld, 2007). In that study,
the social networks of 1730 non-delinquent, minor
delinquent and serious delinquent
pupils at lower-
level secondary schools in the Netherlands were
analysed. This paper only reports about the first step,
the model and simulations.
In Section 2 a summary from the literature on
social learning is presented. Section 3 discusses the
chosen modelling approach. The simulation model is
presented in Section 4, and Section 5 discusses
simulation results. In Section 6, these results are
analysed using formal techniques. Section 7 presents
related work. Finally, Section 8 concludes the paper.
2 SOCIAL LEARNING
According to (Moffitt, 1993), two types of
delinquents can be distinguished: life-course-
persistent offenders, who stay criminal throughout
their entire life and adolescence-limited offenders,
who only show antisocial behaviour during
5
Bosse T., Gerritsen C. and C. A. Klein M. (2009).
AGENT-BASED SIMULATION OF SOCIAL LEARNING IN CRIMINOLOGY .
In Proceedings of the International Conference on Agents and Artificial Intelligence, pages 5-13
DOI: 10.5220/0001512000050013
Copyright
c
SciTePress

adolescence. Life-course-persistent anti-social
behaviour is caused by neuropsychological problems
during childhood that interact cumulatively with
their criminogenic environments across
development, which leads to a pathological
personality. Adolescence-limited antisocial
behaviour is caused by the gap between biological
maturity and social maturity. It is learned from
antisocial models that are easily mimicked, and it is
sustained according to the reinforcement principles
of learning theory. They peak sharply at about age
17 and drop fast in young adulthood. In the current
paper, we explicitly focus on the adolescence-
limited offenders.
An influential theory on the emergence of
adolescence-limited criminal behaviour is the
differential association theory, which was first
proposed by Sutherland and Cressey (1966) and later
expanded by Burgess and Akers (1966). In short,
this (informal) theory states that behaviour is learned
through interaction with others. We learn most from
the people we are in close contact with, like parents
and peers. There are two basic elements to
understanding the differential association theory.
First, the content of what is learned is important
(e.g., motives, attitudes and evaluations by others of
the meaningful significance of each of these
elements). Second, the process by which learning
takes place is important, including the intimate
informal groups and the collective and situational
context where it occurs. Criminal behaviour itself is
learned through assigning meaning to behaviour,
experiences, and events during interaction with
others.
According to Sutherland and Cressey (1966), the
extent to which delinquent behaviour is imitated is
influenced by the frequency, duration, and intensity
of the contact. Frequent, long and important or
prestigious contacts have a larger influence. In
addition, the priority of learning influences the
social learning process: the earlier behaviour is
learned, the more influential it is.
3 MODELLING APPROACH
To formalise and analyse the emergence of criminal
behaviour through social learning from an agent
perspective, an expressive modelling language is
needed. On the one hand, qualitative aspects have to
be addressed, such as certain characteristics about
the agents (e.g., their age), their social relationships
(e.g., who are their parents and friends). On the other
hand, quantitative aspects have to be addressed. For
example, an agent’s level of delinquency, which is
the extent to which an agent exhibits delinquent
behaviour, can best be described by a real number.
The change of this delinquency can best be
described by a mathematical formula. Another
requirement of the chosen modelling language is its
suitability to express on the one hand the basic
mechanisms of social learning (for the purpose of
simulation), and on the other hand more global
properties of social learning (for the purpose of
logical analysis and verification). For example, basic
mechanisms of social learning involve decisions of
individual agents to attach to their peers, whereas
global properties are statements that consider the
learning process over a longer period, like
“eventually the delinquent pupils become less
delinquent”.
The predicate-logical Temporal Trace Language
(TTL) (Bosse et al., 2006) fulfils all of these
desiderata. It integrates qualitative, logical aspects
and quantitative, numerical aspects. This integration
allows the modeller to exploit both logical and
numerical methods for analysis and simulation.
Moreover it can be used to express dynamic
properties at different levels of aggregation, which
makes it well suited both for simulation and logical
analysis.
TTL is based on the assumption that dynamics
can be described as an evolution of states over time.
The notion of state as used here is characterised on
the basis of an ontology defining a set of physical
and/or mental (state) properties that do or do not
hold at a certain point in time. These properties are
often called state properties to distinguish them
from dynamic properties that relate different states
over time. A specific state is characterised by
dividing the set of state properties into those that
hold, and those that do not hold in the state.
Examples of state properties are ‘agent 1 has a
delinquency level of 0.35’, or ‘agent 2 has an
attachment to agent 3 of 0.5’.
To formalise state properties, ontologies are
specified in a (many-sorted) first order logical
format: an ontology is specified as a finite set of
sorts, constants within these sorts, and relations and
functions over these sorts (sometimes also called
signatures). The examples mentioned above then can
be formalised by n-ary predicates (or proposition
symbols), such as, for example,
has_delinquen-
cy(agent1,0.35)
or has_attachment_to(agent2, agent3,
0.5)
. Such predicates are called state ground atoms
(or atomic state properties). For a given ontology
Ont, the propositional language signature consisting
of all ground atoms based on
Ont is denoted by
APROP(Ont). One step further, the state properties
based on a certain ontology
Ont are formalised by the
ICAART 2009 - International Conference on Agents and Artificial Intelligence
6

propositions that can be made (using conjunction,
negation, disjunction, implication) from the ground
atoms. Thus, an example of a formalised state
property is has_delinquency(agent1,0.35) & has_delin-
quency(agent2,0.45)
. Moreover, a state S is an
indication of which atomic state properties are true
and which are false, i.e., a mapping
S: APROP(Ont) →
{true, false}
. The set of all possible states for ontology
Ont is denoted by STATES(Ont).
To describe dynamic properties of complex
processes such as the development of criminal
behavior, explicit reference is made to time and to
traces. A fixed time frame
T is assumed which is
linearly ordered. Depending on the application, it
may be dense (e.g., the real numbers) or discrete
(e.g., the set of integers or natural numbers or a
finite initial segment of the natural numbers).
Dynamic properties can be formulated that relate a
state at one point in time to a state at another point in
time. A simple example is the following (informally
stated) dynamic property about the delinquency of
agents:
For all traces γ,
there is a time point t such that
all agents have a delinquency that is lower than d.
A trace γ over an ontology Ont and time frame T
is a mapping γ : T → STATES(Ont), i.e., a sequence of
states
γ
t
(t ∈ T) in STATES(Ont). The temporal trace
language TTL is built on atoms referring to, e.g.,
traces, time and state properties. For example, ‘in
trace
γ at time t property p holds’ is formalised by
state(γ, t) |= p. Here |= is a predicate symbol in the
language, usually used in infix notation, which is
comparable to the
Holds-predicate in situation
calculus. Dynamic properties are expressed by
temporal statements built using the usual first-order
logical connectives (such as ¬, ∧, ∨, ⇒) and
quantification (∀ and ∃; for example, over traces,
time and state properties). For example, the
informally stated dynamic property introduced
above is formally expressed as follows:
∀γ:TRACE ∃t:TIME ∀a:AGENT ∃x:REAL
state(γ, t) |= has_delinquency(a, x) & x≤d
In addition, language abstractions by introducing
new predicates as abbreviations for complex
expressions are supported.
To be able to perform (pseudo-)experiments, only
part of the expressivity of TTL is needed. To this
end, the executable LEADSTO language (Bosse et
al., 2007) has been defined as a sublanguage of TTL,
with the specific purpose to develop simulation
models in a declarative manner. In LEADSTO,
direct temporal dependencies between two state
properties in successive states are modelled by
executable dynamic properties. The LEADSTO
format is defined as follows. Let α and β be state
properties as defined above. Then, the notation α →→
e, f, g, h β means:
If state property α holds for an interval with duration g,
then after some delay between e and f
state property
β
will hold for an interval with duration h.
As an example, the following executable dynamic
property states that “if during 1 time unit the
attachment between agent a1 and a2 is x1, and the
difference in delinquency between both agents is x2,
then for the next 5 time units (after a delay between
0 and 0.5 time units) the attachment between both
agents will be
β*x1+(1-β)*|x2|”:
∀a1,a2:AGENT ∀x1,x2:REAL
has_attachment_to(a1,a2,x1) ∧
delinquency_difference(a1,a2,x2) →→
0, 0.5, 1, 5
has_attachment_to(a1,a2,β*x1+(1-β)*|x2|)
Based on TTL and LEADSTO, two dedicated
pieces of software have recently been developed.
First, the LEADSTO Simulation Environment
(Bosse et al., 2007) takes a specification of
executable dynamic properties as input, and uses this
to generate simulation traces. Second, to
automatically analyse the resulting simulation traces,
the TTL Checker tool (Bosse et al., 2006) has been
developed. This tool takes as input a formula
expressed in TTL and a set of traces, and verifies
automatically whether the formula holds for the
traces. In case the formula does not hold, the
Checker provides a counter example, i.e., a
combination of variable instances for which the
check fails.
4 SIMULATION MODEL
To study the influence of social learning on
delinquent behaviour, we modelled a school class
with 10 pupils. There are three groups that influence
the process of social learning, namely parents,
school and peers. Therefore, each pupil is
represented as an agent; the parents of the pupils and
the school are modelled as groups. Each pupil is
related to one parent group. The agents have a
number of characteristics in our model (determined
based on discussions with experts). We restricted
our study to the characteristics that are collected in
the empirical study (Weerman and Bijleveld, 2007).
The first property of an agent is its age. In our model
the age is restricted to values between 12 and 17.
The age is relevant for influence of peers on each
other. The older an adolescent is (up to 17) the more
AGENT-BASED SIMULATION OF SOCIAL LEARNING IN CRIMINOLOGY
7

his behaviour is influenced by peers. In addition, the
age difference between peers is relevant, since older
people are often more dominant in the relationship.
The influence of school and parents tends to
decrease as the adolescent gets older.
In addition, agents have a basic level of
influenceability: this represents how easily they can
be influenced. Oppositely, agents and groups have a
level of dominance: this represents how easily they
can influence others. For persons this is a character
trait. Schools can also have a level of dominance. A
dominant school can be seen as a strict school, while
a school that is less strict could be considered to be
less dominant.
The social relations between pupils in a school
class are modelled via attachment relations. All
agents are attached to each other with a specific level
of attachment, representing the intensity of the
contact as defined by Sutherland and Cressey
(1966). The attachment relation is also used to
model the attachment of pupils to their parents and
to their school. We assume that a high attachment
results in a higher influence of the attached agent or
group on the behaviour of the pupil.
Finally, we model a level of delinquency for all
agents and groups, also for parents and schools. The
initial value for the delinquency of an agent could be
based on a measurement of the number of delinquent
acts of a pupil in the past. The interpretation of the
delinquency of a school is indirect: the school has a
low level of delinquency if it is a good school, i.e.
teachers and other staff members have a low level of
delinquency. When the atmosphere in the school is
less positive, then it has a higher level of
delinquency.
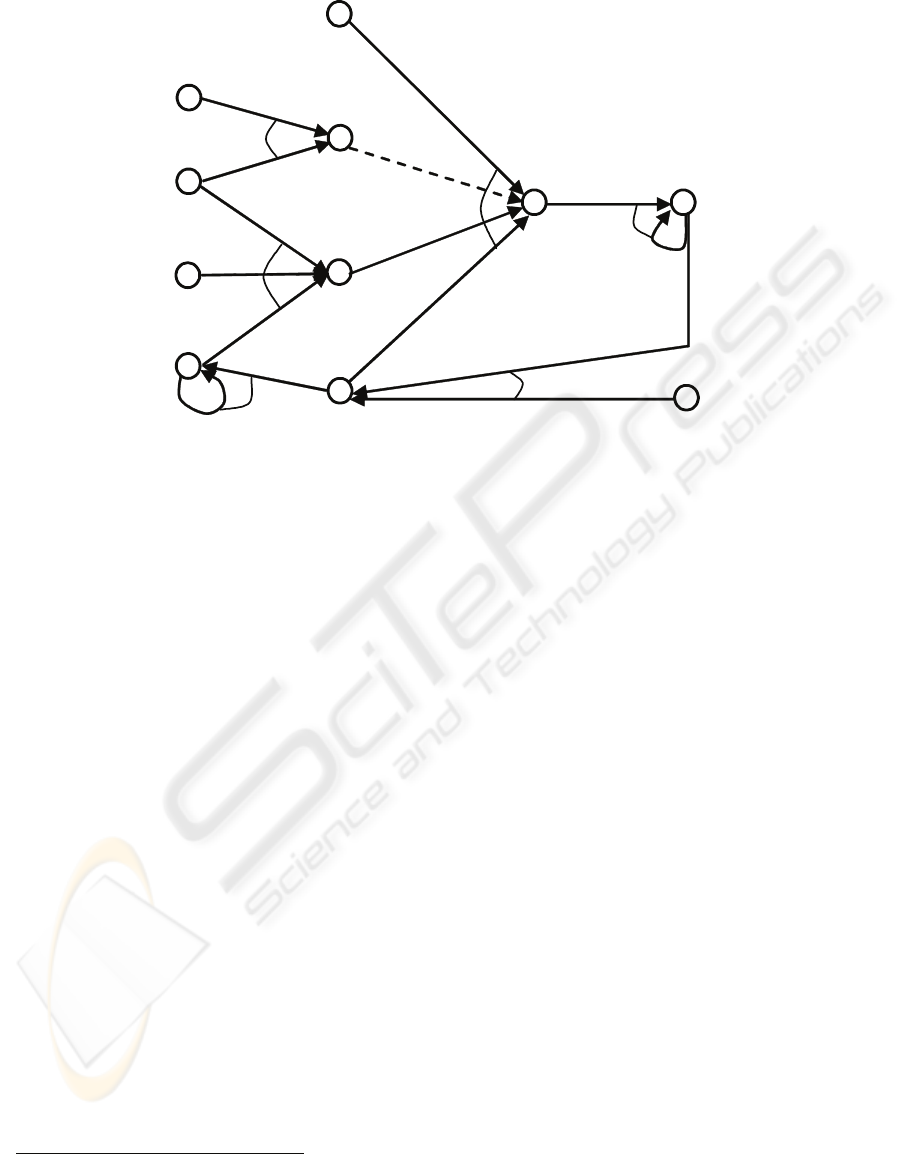
During the simulation, the levels of delinquency
of the pupils change because of the influence of
others. This process is depicted in Figure 1, where
the circles denote state properties and the arrows
denote dynamic properties (relationships) between
them. The age of each agent increases every year.
Every agent starts with a basic influenceability;
together with the age of the agent and the attachment
to a specific group or agent, the effective
influenceability of the agent by that agent or group is
determined (denoted by
has_influenceability in Figure
1).
This effective influenceability is combined with
the level of dominance of the other party, the
difference in delinquency between the agent and the
other party, and - in case the other party is an agent -
the age difference between two agents. This leads to
the so-called delta delinquency. The delta
delinquency represents all factors that influence the
level of delinquency of an agent. In order to
calculate the new delinquency of an agent, the delta
delinquencies of all agents and groups in its
environment are combined with the old delinquency
(the delinquency the agent started out with).
In addition, the model is able to adapt the
attachment between the agents. The idea behind this
is that the strength of a relation is influenced by the
overlap in values. If the difference in the level of
delinquency is very high, then the attachment will
decrease. However, because there are many other
factors that influence the attachment as well, the
difference in delinquency only causes a minor
change in attachment.
In the model, the concepts of influenceability,
dominance, attachment, and delinquency are
modelled as a real number between 0 and 1.
Furthermore, the age is modelled as an integer
between 12 and 17, and the delta delinquency as a
real number between -1 and 1. The relationships
between the concepts have been modelled in
LEADSTO. Two example relationships (to
determine the delta delinquency of groups, and the
new delinquency, respectively) are stated below.
Here, the β’s are decay factors, and the w’s are
weight factors. Note that these relationships
correspond to (conjunctions of) arrows in Figure 1.
The complete set of LEADSTO relationships is
shown in the online appendix
1
.
Delta Delinquency Determination (for Groups)
∀a:AGENT ∀g:GROUP ∀x1,x2,x3:REAL
delinquency_difference(a,g,x1) ∧ has_influencability(a,g,x2) ∧
has_dominance(g,x3) →→
has_delta_delinquency(a,g,β2*(β1*x1+(1-β1)*x1*
(w4*x2+w5*x3)))
New Delinquency Determination
∀a1:AGENT ∀g:GROUP ∀d,s,p,x1,...,x10:REAL
has_old_delinquency(a1,d) ∧
has_delta_delinquency(a1,school,s) ∧
has_delta_delinquency(a1,g,p) ∧ are_parents_of(g,a1) ∧
has_delta_delinquency(a1,agent1,x1) ∧ ...
has_delta_delinquency(a1,agent10,x10) →→
has_delinquency(a, d+ (s+p+x1+...+x10)/12))
5 SIMULATION RESULTS
A number of simulation experiments have been
performed to see whether the behaviour of the model
was as expected for some common scenarios. A
thorough evaluation will be performed later when
the results will be compared with data of an
empirical study. A longer description with more
scenarios and details can be found in the appendix.
1
http://human-ambience.few.vu.nl/docs/ICAART09.pdf
ICAART 2009 - International Conference on Agents and Artificial Intelligence
8
has_basic_
influenceability(a,x)
has_influenceability
(a,gr,x)
has_dominance
(gr,x)
has_attachment_to
(a,gr,x)
has_delinquency
(gr,x)
has_delinquency
(a,x)
has_delta_
delinquency
(a,gr,x)
has_age(a,x)
delinquency_
difference(a,gr,x)
age_difference
(a,a2,x)
has_age(a2,x)
Figure 1: Concepts and relations in the simulation model.
In the first scenario there is one bad guy with
criminal parents in an otherwise reasonable school
class. We are interested in the question whether the
criminal boy makes the other boys bad or whether
the group is able to straighten out the delinquent. In
this scenario agent 1 has a delinquency of 0.8 while
the other agents have a delinquency of 0.3. All
agents are male2 and are 12 years old at the start of
the simulation. They have a basic influenceability
with a value of 0.4, a level of dominance of 0.6 and
a mutual attachment of 0.3. The attachments are
stable in this simulation. Every agent has parents
with a dominance of 0.7 and a delinquency of 0.2,
except for agent 1, whose parents have a
delinquency of 0.8.
The resulting trace is shown in Figure 2 (this and
the following figures can be found at the last page of
the paper). Here, time is on the horizontal axis and
the level of delinquency is on the vertical axis. The
three graphs show the combined delinquencies of all
pupils, the delinquency of agent 1 and the
delinquency of the other agents (that all show the
same behaviour; agent 10 is just taken as an
example), respectively. The two lines in the first
graph correspond to the lines in the second and third
graph, respectively, where a more detailed scale is
2
Note that the model does not incorporate a direct influence of
gender. Difference between male and female pupils can be
modeled indirectly by giving the males higher initial
delinquencies.
used. The results show that the interaction between
the agents leads to a decreased delinquency of agent
1. The delinquency of the other agents increases
slightly to 0.31 and from this point on it decreases to
0.255 at time point 100. From time point 70 on,
there is a more or less stable difference in
delinquency between the agent with criminal parents
and the others.
In a second scenario (Figure 3), the influence of
the school is examined by increasing its delinquency
to 0.8. The level of delinquency of the agents and
their parents were identical to the settings in the
previous scenario. The results show that the
increased delinquency of the school causes an
increased level of delinquency of all the agents. This
influence appeared to be larger than the influence of
individual agents, because it propagates through to
pupils, who again influence each other.
In the third scenario, half of the pupils (and
their parents) have a high delinquency. The other
pupils (and their parents) have the same level of
delinquency as in scenario 1. In this case all agents
influence each other and their delinquencies grow
towards each other, while a difference remains
because of the influence of the parents (see Fig. 4).
Finally, the fourth scenario represents a school
class with two groups (3 delinquent pupils with a
high mutual attachment, 3 extremely non-delinquent
pupils with a high mutual attachment) and 4
individuals with a high basic influenceability. One
of these ‘group-less pupils’ has a high attachment to
AGENT-BASED SIMULATION OF SOCIAL LEARNING IN CRIMINOLOGY
9

a person in the criminal group, one to a person in the
non-criminal group, and the others had no specific
relations. The attachments can change over time.
The goal of this scenario is to see whether a pupil
will be incorporated in a group if he has a strong
relationship with one of them. Figure 5 shows the
resulting delinquencies.
Interestingly, we see that all group-less pupils
reach a level of delinquencies that is close to that of
the pupils in the ‘good group’, even for the pupils
that have a strong relation to a pupil in one of the
groups. This observation can be explained by the
fact that the delinquency of the parents of the group-
less pupils is close to the delinquency of the parents
in the good group. However, if we look closely at
the delinquencies of the group-less people (lower
graph in Figure 5), we see that they develop slightly
differently (notice the different scale). Apparently,
the delinquency of the pupil with a friend in the bad
(good) group initially grows faster (slower), but
eventually it reaches the same level as the other
group-less pupils.
6 FORMAL ANALYSIS
The detailed settings and results of ten simulation
experiments (including the ones described in Section
5) are shown in the appendix. Among the different
experiments, various parameter settings were varied,
in particular the initial delinquencies of agents,
parents, and school, the initial attachment between
agents, and several weight factors.
To analyse the resulting simulation traces in
more detail, the TTL Checker tool (Bosse et al.,
2006) has been used. As mentioned earlier, this tool
takes as input a TTL formula and a set of traces, and
verifies automatically whether the formula holds for
the traces. For the current domain, a number of
hypotheses have been expressed as dynamic
properties in TTL, which were inspired by relevant
questions in Criminology (see Sections 1 and 2). To
give a simple example, consider the following
dynamic property (P1), which expresses that the
delinquency of an agent keeps on decreasing over
time:
P1 Strict Monotonic Decrease of Delinquency
For all time points t1 and t2, if t2 is later than t1, then the
agent’s delinquency at t2 is lower than at t1.
P1(γ:TRACE, a:AGENT) ≡
∀t1,t2:TIME ∀d1,d2:REAL
[ state(γ, t1) |= has_delinquency(a, d1) &
state(γ, t2) |= has_delinquency(a, d2) & t1<t2 ] ⇒ d1>d2
Note that this formula comprises two free
variables (the trace
γ and the agent a), for which
different values can be instantiated. For example, in
order to check whether agent 1 satisfies the criterion
of strict monotonic decrease of delinquency in
simulation trace 5, the formula
P1(trace1, agent1)
should be checked. Similarly, it is possible to check
whether the property holds for all agents and all
traces, or for a certain percentage of them.
Besides checking whether the delinquency of
agents keeps on decreasing, also other properties can
be verified. A relevant question in Criminology is
what the relative influences of (respectively) parents,
peers, and school on the development of a person’s
delinquency are. For example, might it be the case
that the biggest contribution is provided by parents
and school only, and that the influence of classmates
can almost be neglected? To analyse these kinds of
hypotheses, properties like the following have been
established:
P2 Agent Converges to Parents and School
At the end of the trace, the delinquency of agent a lies within
a margin δ of the average of the delinquencies of its parents
and the school at the start of the trace.
P2(γ:TRACE, a:AGENT) ≡
∀d1,d2,d3:REAL ∀p:AGENT
[ state(γ, start_time) |= has_delinquency(p, d1) &
state(γ, start_time) |= has_delinquency(school, d2) &
state(γ, end_time) |= has_delinquency(a, d3) &
are_parents_of(p,a) & ]
⇒ d3-δ < (d1+d2)/2 < d3+δ
If this property were true (for a small δ), this
would indicate that the development of a pupil could
be predicted by taking into account the delinquency
of the parents and the school only. Some initial
checks have pointed out that the lowest δ for which
the property satisfies all generated traces is 0.22. In
other words, for all of the traces the influence of
parents and school was relatively high. In addition to
P2, a property was created to compare the change in
delinquency between two agents a1 and a2.
P3 Bigger Change in Delinquency
During the whole trace, agent a1 made a bigger change in
delinquency than agent a2.
P3(γ:TRACE, a1,a2:AGENT) ≡
∀d1,d2,d3,d4:REAL
[ state(γ, start_time) |= has_delinquency(a1, d1) &
state(γ, start_time) |= has_delinquency(a2, d2) &
state(γ, end_time) |= has_delinquency(a1, d3) &
state(γ, end_time) |= has_delinquency(a2, d4) ]
⇒ |d1-d3| > |d2-d4|
This property can be used, for example, to find
out whether in a school class with many “good”
pupils and one “bad” guy (see scenario 1), the bad
pupil tends to move towards the good ones, or vice
versa. In our simulation traces, such a bad pupil
ICAART 2009 - International Conference on Agents and Artificial Intelligence
10

indeed turned out to converge towards his
classmates.
To summarise, a number of TTL properties have
been checked against the generated simulation
traces, as a first pilot study of the applicability of the
approach. Although no real conclusions can be
drawn as yet, these checks pointed out that the traces
satisfy basic properties that were inspired by
criminological theories, such as property P2 and P3.
Finally, it is important to note that, in addition to
simulated traces, the TTL Checker can also take
empirical traces as input. In future work, several
properties as those introduced here will be verified
against empirical traces that are constructed on the
basis of experiments in real classrooms
7 RELATED WORK
With respect to related work, the research presented
in this paper on the one hand has commonalities
with literature from the social and behavioural
sciences (in particular, the area of Criminology), and
on the other hand with literature in AI and Computer
Science (among others, agent-based simulation).
Concerning the criminological and psychological
area, first of all the current paper is related to early
articles from the 60’s and 70’s such as Bandura
(1977), Burgess and Akers (1966) and Sutherland
and Cressey (1966), which were the first to
formulate (different variants of) the social learning
theory. Here, the theory put forward by Bandura
(1977) is more generic, whereas the other two focus
specifically on social learning in Criminology. For
an overview of these theories, see Lanier and Henry
(1998), Chapter 7. In fact, these theories formed the
basis of the research questions addressed in this
paper. Based on these theories, Opp (1989)
identified a number of (informal) properties that are
expected to hold for social learning in Criminology,
such as “the more frequently persons show deviant
behaviour, the more frequently they will have
contact with patterns of deviant behaviour”.
Although a detailed verification (using larger-scale
experiments and statistical techniques) is left for
future work, an initial analysis provides evidence
that our model indeed satisfies these properties.
Next, a number of papers in Criminology propose
more refined models for social learning, often
focusing on specific aspects of the learning. For
example, Thornberry et al. (1994) compared three
theoretical models of the interrelations among
associations between delinquent peers, delinquent
beliefs, and delinquent behaviour. A main difference
with our work is that these models are not
computational. Nevertheless, their conclusions are in
agreement with the initial results found in this paper.
Finally, several authors have performed empirical
studies on social learning of delinquent behaviour in
schools (Bruinsma, 1984) and Weerman and
Bijleveld, 2007). Our model was designed explicitly
with the purpose of reproducing such data.
Concerning the literature in AI and Computer
Science, we are not aware of approaches using
multi-agent technology to simulate delinquent
behaviour of individuals in a group. However,
various papers have similarities to the work
proposed here. First, Van Dijkum and Landsheer
(2000) present a model that is rather similar to ours,
but which uses differential equations to describe the
development of juvenile criminal behaviour.
Another difference with our model is that they aim
for an integration of multiple criminological theories
(namely social learning theory, career theory, and
rational choice theory), whereas we focus (in more
detail) on the former only. Moreover, several authors
have created models that address social learning and
criminal behaviour at a more global level. For
example, Chamley (2003) presents an economic
model for social learning, although not explicitly
focussed on learning of delinquent behaviour.
Similarly, Winoto (2002) presents an agent-based
economic model for the market for offenses. This
model addresses the global development of
delinquency in a population. These models differ
from our model in the sense that they are situated at
a macroscopic level, thereby abstracting from
differences between individuals. An approach that
does consider individual differences, but that
addresses a different domain, is presented by
Tsvetovat and Carley (2005). They present a
simulation model of the dynamics of terrorist
networks, based on networks of non-deterministic
finite automata. Furthermore, a large number of
approaches address simulation of the environmental
aspects of criminal behaviour, such as the
displacement of crime and the emergence of “hot
spots”, e.g., Liu et al. (2005) and Bosse and
Gerritsen (2008). Finally, relevant work is put
forward by Conte and Paolucci (2001). They
identify a number of (cognitive) factors that are
relevant in social learning in general. However, in
contrast to our work, they do not provide a
computational model.
8 CONCLUSIONS
This paper presented an agent-based approach to
simulate and formally analyse the process of social
AGENT-BASED SIMULATION OF SOCIAL LEARNING IN CRIMINOLOGY
11

learning of delinquency during adolescence. The
general mechanism of change by influences of peers
is possibly also useful in other domains in which
social learning is relevant. In this paper, however,
we focused on learning of delinquent behaviour.
Inspired by criminological literature, the approach
incorporates the influences of three types of groups,
namely peers, parents, and school. Various relevant
factors were identified, such as influenceability,
dominance, and attachment, and their mutual
relationships were formalised by means of the
hybrid modelling language LEADSTO. Moreover, it
was shown how the approach can be used to
generate simulation traces, and how such traces can
be automatically verified against relevant properties,
expressed in the language TTL. Although
preliminary, the first results are promising. Firstly,
they provide evidence that the proposed model is a
useful experimental tool to give insight in social
learning processes as described in the criminological
literature. Secondly, some interesting patterns have
already been found. For example, the simulation
results suggest that the influence of the school on
delinquency is relatively high (scenario 3), that the
impact of attachment is relatively low (scenario 4),
and that every individual learning process
approaches a final delinquency near the average of
the delinquencies of parents, school, and peers.
In the current paper, no detailed empirical
validation of the model has been presented.
However, as mentioned in the introduction, various
empirical studies have been performed, of which
large data sets are available (Bruinsma, 1985) and
Weerman and Bijleveld, 2007). The model has been
explicitly designed with the objective of using such
data sets for validation in the future. Currently, some
initial steps in this direction are taken. During such a
validation, several questions are addressed, such as
“is it realistic that the average delinquency almost
always decreases?”, or “is it realistic to have a
relatively stable delinquency for school and
parents?”. When these questions are solved, the
model can be further fine-tuned, in particular by
choosing realistic values for all parameter settings
and weight factors involved.
REFERENCES
Bandura, A. (1977). Social Learning Theory. Englewood
Cliffs, NJ, Prentice-Hall.
Bosse, T., and Gerritsen, C., Agent-Based Simulation of
the Spatial Dynamics of Crime: On the Interplay
between Criminal Hot Spots and Reputation. In:
Proceedings of the 7
th
International Joint Conference
on Autonomous Agents and Multi-Agent Systems,
AAMAS’08. ACM Press, 2008, pp. 1129-1136.
Bosse, T., Jonker, C.M., Meij, L. van der, and Treur, J.
(2007). A Language and Environment for Analysis of
Dynamics by SimulaTiOn. International Journal of AI
Tools, vol. 16, issue 3, pp. 435-464.
Bosse, T., Jonker, C.M., Meij, L. van der, Sharpanskykh,
A., and Treur, J. (2006). Specification and Verification
of Dynamics in Cognitive Agent Models. In:
Proceedings of the 6
th
International Conference on
Intelligent Agent Technology, IAT’06. IEEE Computer
Society Press, 2006, pp. 247-254.
Bruinsma, G.J.N. (1985). Crime as Social Learning
Process. A Test of the Differential Association Theory
in the version of K.-D. Opp (in Dutch). Gouda Quint,
Arnhem.
Burgess, R., and Akers, R.L. (1966). A Differential
Association-Reinforcement Theory of Criminal
Behavior. Social Problems, vol. 14, pp. 363-383.
Chamley, C.P. (2003). Rational Herds: Economic Models
of Social Learning. New York: Cambridge University
Press.
Conte, R., and Paolucci, M. (2001). Intelligent Social
Learning. Journal of Artificial Societies and Social
Simulation, vol. 4, issue 1.
Dijkum, C. van, and Landsheer, H. (2000). Experimenting
with a Nonlinear Dynamic Model of Juvenile Criminal
Behavior. Simulation & Gaming, vol. 31, pp. 479-490.
Gottfredson, M. and Hirschi, T. (1990). A General Theory
of Crime. Stanford University Press.
Lanier, M.M., and Henry, S. (1998). Essential
Criminology. Boulder, CO: Westview Press.
Liu, L., Wang, X., Eck, J., and Liang, J. (2005).
Simulating Crime Events and Crime Patterns in
RA/CA Model. In F. Wang (ed.), Geographic
Information Systems and Crime Analysis. Singapore:
Idea Group, pp. 197-213.
Moffitt, T.E. (1993). Adolescence-Limited and Life-
Course-Persistent Antisocial Behavior: A
Developmental Taxonomy. Psychological Review, vol.
100, no. 4, pp. 674-701.
Opp, K.D. (1989). The Economics of Crime and the
Sociology of Deviant Behaviour - A Theoretic
Confrontation of Basic Propositions. Kyklos, vol. 42,
issue 3, pp. 405-430.
Sutherland, E.H., and Cressey, D.R. (1966). Principles of
Criminology, 7
th
edition. Philadelphia: J.B. Lippincott.
Thornberry, T.P., Lizotte, A.J., Krohn, M.D., Farnworth,
M., and Jang, S.J. (1994). Delinquent Peers, Beliefs,
and Delinquent Behavior: A Longitudinal Test of
Interactional Theory. Criminology, vol. 32, pp. 47-83.
Tsvetovat, M., and Carley, K.M. (2005). Structural
Knowledge and Success of Anti-Terrorist Activity:
The Downside of Structural Equivalence. Journal of
Social Structure, vol. 6.
Weerman, F.M., and Bijleveld, C.C.J.H. (2007). Birds of
Different Feathers. European Journal of Criminology,
vol. 4, issue 4, pp. 357-383.
Winoto, P. (2002). An Agent-Based Simulation of the
Market for Offenses. In: AAAI Workshop on Multi-
Agent Modeling and Simulation of Economic Systems.
Edmonton, Canada.
ICAART 2009 - International Conference on Agents and Artificial Intelligence
12

Figure 2: Delinquency in a school class with one bad guy.
Figure 3: Influence of a bad school.
Figure 4: Delinquency in a school class with half of the pupils being criminal.
Figure 5: Delinquencies in school class with two groups.
AGENT-BASED SIMULATION OF SOCIAL LEARNING IN CRIMINOLOGY
13
