EFFICIENT SOURCE CODING IN A THRESHOLDING-BASED ECG

COMPRESSOR USING THE DISCRETE WAVELET TRANSFORM

Carlos Hernando Ramiro, Manuel Blanco Velasco, Eduardo Moreno-Mart´ınez

Fernando Cruz Rold´an and Jos´e S´aez Landete

Departamento de Teor´ıa de la Se˜nal y Comunicaciones, Universidad de Alcal´a, Madrid, Spain

Keywords:

ECG compression, Electrocardiogram, Entropy, Maximum compression ratio, Source coding, Thresholding,

Wavelet transform.

Abstract:

The aim of electrocardiogram (ECG) compression is to achieve as much compression as possible while the

signiﬁcant information for diagnosis purposes is preserved in the reconstructed signal. The source coding stage

allows us to modify the compression ratio without quality degradation through a lossless encoder. In this work,

the performance of this stage is analyzed in a compression scheme that has already presented good results

among those from the state of the art. The compressor is based on discrete wavelet transform, thresholding

and two-role encoder. The study consists of ﬁxing all the stages except the source coding one in order to

obtain an upper compression ratio bound. The assessment is based on the entropy of the independent symbols

and the minimum expected length of the codewords. The results reveal a gap to improve the compression

ratio, so from the previous entropy study an alternative compression method is proposed. For this purpose

the symbols probabilities are analyzed through the normalized histogram. Thus, a Huffman encoder instead

of the two-role one is applied in the new compressor to attain the maximum compression ratio. In this way a

signiﬁcant improvement is obtained without decreasing the original retrieved quality.

1 INTRODUCTION

The electrocardiogram (ECG) provides essential in-

formation to cardiologists for diagnosing. Therefore,

ECG processing has been a topic of great interest

and is most commonly used in applications such as

monitoring. Since 1961, when Holter (Holter, 1961)

introduced new techniques to monitor continuously

the electrical activity of ambulatory patients, ECG

recording techniques have gone through constant evo-

lution. The current ECG recording systems allow to

gather long-term signals with a duration of several

hours in a simple, inexpensive and non-invasive way.

Then the amount of ECG data increases considerably

and compression becomes a necessity in order to pro-

vide storage and transmission solutions.

With this in mind, many compression schemes

have been proposed during the past decades. A short

summary of them can be found in (Blanco Velasco

et al., 2004b). Among them, the lossy compression

techniques achieve great compression results at the

expense of some distortion in the original signal. The

point is that the lost information must be the irrelevant

from the diagnosis view (e.g. noise, lowest power fre-

quencies, etc.), which in terms of the ECG means that

the morphology of the reconstructed signal does not

change signiﬁcantly. Recently, several thresholding-

based compression algorithms using signal decompo-

sition techniques have been developed (Abo-Zahhad

and Rajoub, 2002; Benzid et al., 2003; Chen et al.,

2006; Blanco Velasco et al., 2004b; Blanco Ve-

lasco et al., 2004a; Benzid et al., 2007; Blanco Ve-

lasco et al., 2007), because they yield attractive per-

formance and low computational cost. The typical

block diagram of this kind of compressors is shown

in ﬁgure 1. Although some of them utilize modern

techniques for the decomposition of the original sig-

nal such as nearly-perfect reconstruction cosine mod-

ulated ﬁlter banks (N-PR CMFB) (Blanco Velasco

et al., 2004b; Blanco Velasco et al., 2004a) or wavelet

packets (WP) (Blanco Velasco et al., 2007) with good

results, most of them are based on the discrete wavelet

transform (DWT), which play an interesting role in

the ECG data compression applications owing to their

easy implementation and efﬁciency (Abo-Zahhad and

Rajoub, 2002; Benzid et al., 2003; Chen et al., 2006;

259

Ramiro C., Velasco M., Moreno-Martínez E., Roldán F. and Landete J. (2009).

EFFICIENT SOURCE CODING IN A THRESHOLDING-BASED ECG COMPRESSOR USING THE DISCRETE WAVELET TRANSFORM.

In Proceedings of the International Conference on Bio-inspired Systems and Signal Processing, pages 259-264

DOI: 10.5220/0001533502590264

 SciTePress

x[n]

y[n]

c[n]

SIGNAL

DECOMP.

THRESHOLDING

y [n]

y[n]

PCM

QUANTIZATION

SOURCE

CODING

Figure 1: Block diagram of a typical thresholding-based

compressor using signal decomposition.

Benzid et al., 2007).

In this paper, the study is focused on the

thresholding-based compressors using DWT. The

source coding stage of this kind of compression

schemes is analyzed in order to obtain the maximum

compression ratio (CR

max

). For this purpose the rest

of the blocks presented in ﬁgure 1 are ﬁxed utilizing

the compression scheme proposed in (Benzid et al.,

2007). Then the statistical analysis of the indepen-

dent symbols used in the source encoder is performed

and an upper bound of the compression ratio is de-

rived. Provided that some gap exists for source co-

ding, we propose a new strategy to increase the com-

pression ratio. Therefore a new compression scheme

that yields better compression ratio (CR) is proposed.

2 THRESHOLDING-BASED

COMPRESSORS

This type of compression schemes takes advantage

of a signal transformation into a domain where the

contribution of some coefﬁcients to the reconstruc-

ted signal morphology is less important than others.

A common technique would be to cancel the less

signiﬁcant wavelet coefﬁcients, producing large runs

of zeros. These bursts of zeros favor the compres-

sion through source coding implementation. Thus the

original sample values are discarded and the quality of

the retrieved signal is degraded. To perform this pro-

cedure, a threshold value must be determined. This

parameter ﬁxes the edge between the deleted samples

and the signiﬁcant ones. The threshold depends on

quality and compression requirements whatever the

aim is. Then the threshold can be ﬁxed beforehand

(Abo-Zahhad and Rajoub, 2002; Benzid et al., 2003;

Chen et al., 2006) or be adjusted according to the de-

sired results (Blanco Velasco et al., 2004b; Blanco

Velasco et al., 2004a; Benzid et al., 2007; Blanco Ve-

lasco et al., 2007).

The signiﬁcant coefﬁcients are quantized through

pulse code modulation (PCM). Finally, a lossless en-

coder is applied to the full sequence that includes the

successions of zeros and the quantized signiﬁcant co-

efﬁcients altogether. This coding procedure consists

of two main steps:

• Determining the independent symbols to repre-

sent the original signal that will be later encoded.

• Selecting the codewords that will encode each one

of those symbols.

In this study, tests with this kind of compre-

ssors are carried out using the MIT-BIH Arrythmia

Database. As measurement criteria to evaluate the

quality of the retrieved signal two parameters are

used. One is the percentage root-mean-square diffe-

rence (PRD), which is deﬁned as:

PRD =

∑

n=1

(x[n] − ˆx[n])

∑

n=1

(x[n])

× 100, (1)

where x[n] is the original ECG signal and ˆx[n] is the

reconstructed one. Since the PRD is strongly depen-

dent on the signal mean value, high mean values can

mask the real quality performance assessment. To

avoid this, we also use the modiﬁed criterion as fo-

llows:

PRD1 =

∑

n=1

(x[n] − ˆx[n])

∑

n=1

(x[n] − ¯x[n])

× 100, (2)

where ¯x[n] is the signal mean value. Furthermore,

it is established in (Zigel et al., 2000), that if the

PRD1 value is between 0 and 9, the quality of the

reconstructed signal is either ‘good’ or ‘very good’,

whereas if the value is greater than 9, its quality group

cannot be determined.

Moreover the CR value is calculated as follows:

CR =

, (3)

where b

is the amount of bits used to represent the

original ECG signal x[n] and b

is the total number of

bits obtained after the source encoder block to repre-

sent c[n].

3 COMPRESSION METHODS

The ﬁrst compression scheme used in this work is

based on that of proposed in (Benzid et al., 2007). It

utilizes discrete wavelet transform (DWT) and thres-

holding. The threshold is obtained through an itera-

tive approach that ﬁnishes when the PRD reaches the

PRD target (PRD

target

) as is proposed in (Blanco Ve-

lasco et al., 2004a). The compressor consists of the

following main steps:

BIOSIGNALS 2009 - International Conference on Bio-inspired Systems and Signal Processing

260

1. Choose the PRD

target

and apply the DWT, up to

the ﬁfth level and with the mother wave “bior4.4”.

2. Threshold the wavelet coefﬁcients with an ite-

rative algorithm in order to match the PRD

target

within a tolerance of 1%.

3. Quantize in PCM the nonzero wavelet coefﬁ-

cients. The quantization resolution B is chosen in

an adaptive way. The value of B is increased until

the PRD matches the PRD

target

, with a tolerance

of 10%.

4. Lossless source coding of the thresholded and

quantized coefﬁcients by means of the two-role

encode (TRE) technique, which consists of the

following:

(a) A baseline of 2

is added to the signiﬁcant coe-

fﬁcients. Then each of them is coded with B+1

bits.

(b) The runs of zeros are also coded also with B+ 1

bits. The minimum encodable length is 1 and

the maximum is 2

− 1, this way these code-

words are different from those used in the pre-

vious point. Thus longer successions of zeros

must be represented with more than one code-

word.

The other compression scheme differs from the

ﬁrst one in the 5th stage. In this case, the lossless

source coding is carried out with a Huffman encoder

(Skretting, 1999) although using the same symbols as

obtained with the TRE method. Thus shorter code-

words are assigned to less probable symbols and the

expected length of the codeword is reduced since the

symbol probabilities are different. In the Huffman en-

coder, the logarithmic encoding and the iterative se-

quence splitting options have been disabled in order to

preserve the original independent symbol set. There-

fore a fair comparison analysis between the compre-

ssion and quality results of both methods can be done.

4 UPPER COMPRESSION RATIO

BOUND ACHIEVEMENT

The CR

max

that can be achieved with a lossless source

encoder is studied in order to obtain an upper com-

pression bound. To do so, the entropy of the indepen-

dent symbols used as input in the source coding stage

is analyzed.

The source entropy deﬁnes a boundary to the ex-

pected length of any instantaneous code (Cover and

Thomas, 2006):

Teorema 1. The expected length L of any instanta-

neous D-ary code for a random variable X is greater

than or equal to the entropy H

(X), with equality

when D

−l

= p

, where p

is the symbol i probability

and l

its corresponding codeword length.

L ≥ H

(X). (4)

The procedure to derive CR

max

in the compressor

schemes described in section 3 consists of the follo-

wing steps:

1. The independent symbol set used to encode is

chosen. The independent symbols are deﬁned as

those that present a biunique relationship with the

ﬁnal codewords. In our case the full symbol set

includes two different subsets:

• The runs of zeros with length less or equal than

− 1.

• The signiﬁcant coefﬁcients, which are quan-

tized with B bits.

Thus the independent symbol set consists of

B+1

− 1 different symbols, as the value 0 is use-

less because there are not successions of zeros

with this length.

2. The probability mass p(x) of the random variable

X is calculated. Then the entropy is derived, con-

sidering the binary alphabet D = {0, 1}:

H(X) = −

∑

x∈H

p(x) log p(x). (5)

3. The CR is obtained as a result of two independent

compression processes: PCM quantization stage

and source coding. For PCM quantization, the

compression ratio CR

only depends on the re-

solution B used. The lower B, the greater CR

On the other hand, the compression ratio of the

source coding CR

can be improved without mo-

difying the quality of the retrieved signal. Accor-

ding to theorem 1, the entropy establishes a bound

to the expected length L of the codeword and con-

sequently to CR

as follows:

≤

. (6)

Therefore, the relation

can be considered as the

upper bound of CR

(CR

2max

4. To obtain CR

max

, the CR

value is also needed. It

follows this equation:

, (7)

where B

is the original sample resolution, whose

value is 11 for this database, and B refers to the

quantization resolution.

5. Finally the CR

max

value can be calculated apply-

ing the following equation:

max

= CR

·CR

2max

. (8)

EFFICIENT SOURCE CODING IN A THRESHOLDING-BASED ECG COMPRESSOR USING THE DISCRETE

WAVELET TRANSFORM

261

5 EXPERIMENTAL STUDY

Tests are carried out using signals from the MIT-BIH

Arrythmia Database. Files in the database contain two

leads sampled at 360 Hz with 11 bits per sample of

resolution. The signal length taken is 182 seconds,

that is 65520 samples per signal. This value is very

close to the two to a power 2

(65536), which allows

us to speed the DWT computing up. Moreover the

1024-baseline added to each lead for storage purposes

is removed before processing.

A statistical study with the signal 117 is ﬁrstly

done. The independent symbols used as input in

the source encoder are obtained and the normalized

histogram is calculated. Moreover the reconstructed

waveform is derived and the error signal is calcu-

lated as the difference between the original and the

retrieved samples. The PRD

target

as well as the qua-

lity and compression results are presented in table 1.

Figure 2 shows the histogram. Two graphs are ob-

tained because the whole set of symbols is split into

two groups as explained in section 4. Note in the his-

togram of ﬁgure 2 that symbols in the run of zeros

have null probability while others are clearly much

more likely. Symbols with null probability which

does not need any codeword, so it is not necessary

to encode them. Also shorter as possible codewords

must be assign to the more frequent symbols.

Moreover the ﬁrst 4096 samples of the original,

retrieved and error signal are shown in ﬁgure 3. The

cardiologists actually diagnose through visual analy-

sis of the ECG, so both waveforms must look as si-

milar as possible. In this case, taking into account the

great upper compression bound obtained, an optimal

visual quality of the reconstructed signal is attained.

Furthermore the error is equally distributed over time,

so cannot mask signiﬁcantly any part of the signal by

accumulation.

Table 1: Upper compression bound for signal 117.

Signal PRD

target

B CR

max

PRD PRD1

117 2 7 17.24 2.12 8.01

The ﬁrst compression study is also carried out

with the signal 117. Several values of B are taken

in order to check the efﬁciency of the adaptive quanti-

zation technique. The results are shown in table 2. As

can be seen, the criterion to select B holds for B = 7,

which is that of chosen by the adaptive quantization

procedure in table 1. This strategy permits to reduce

the value of B, and as a result increases the CR, in

a dynamic way according to the nature of each ECG

signal. So the adaptive quantization algorithm is re-

0 20 40 60 80 100 120

0.01

0.02

0.03

0.04

0.05

Símbolos

(a)

140 160 180 200 220 240

0.01

0.02

0.03

0.04

0.05

0.06

0.07

0.08

Símbolos

(b)

Figure 2: Normalized histograms of signal 117 for

PRD

target

= 2. (a) Runs of zeros (b) Signiﬁcant coefﬁcients.

0 500 1000 1500 2000 2500 3000 3500 4000

−400

−200

200

Amplitude

Original 117 signal

0 500 1000 1500 2000 2500 3000 3500 4000

−400

−200

200

Amplitude

Reconstructed 117 signal

0 500 1000 1500 2000 2500 3000 3500 4000

−20

−10

Error signal

Amplitude

Figure 3: Compression waveform of signal 117 for

PRD

target

= 2.

vealed as efﬁcient and valuable to be included in the

quantization stage of the proposed method. Also the

compression ratios are greater and closer to the upper

bound for all the tested B values.

Another study is performed with the dataset com-

BIOSIGNALS 2009 - International Conference on Bio-inspired Systems and Signal Processing

262

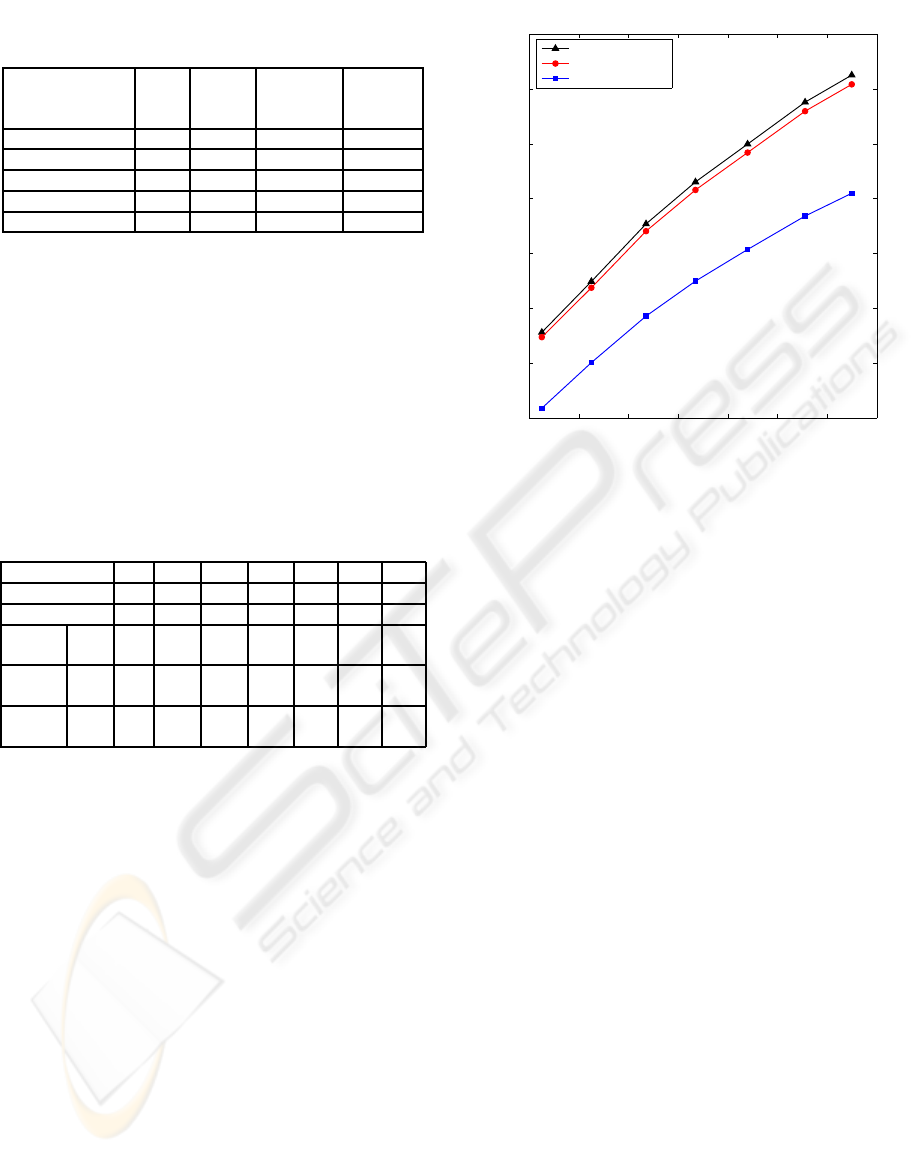
Table 2: Quality and compression results as a function of B

for the 117 signal.

PRD

target

= 2 PRD CR

max

CR TRE

method

prop.

method

B = 6 2.44 18.68 14.68 18.40

B = 7 2.12 17.24 13.65 16.96

B = 8 2.02 15.73 12.38 15.36

B = 9 2.00 14.33 11.25 13.81

B = 10 1.99 13.11 10.28 12.36

posed of the records 100, 101, 102, 103, 107, 109,

111, 115, 117, 118 and 119. In this case diffe-

rent PRD

target

values are taken, which can be seen in

table 3. In the table 3 we show the averaged CR, PRD

and PRD1 of the whole dataset for different PRD

target

The obtained PRD1 values, except the last one, are all

under 9, which stands for good quality of the recons-

tructed signal. The CR as a function of PRD is shown

in ﬁgure 4. As can be seen in the graphic, our methods

yields better compression ratio in the full range.

Table 3: Compression and quality results for the signal set.

PRD

target

2 2.5 3 3.5 4 4.5 5

PRD 2.13 2.63 3.18 3.67 4.20 4.78 5.25

PRD1 3.77 4.64 5.64 6.51 7.41 8.42 9.27

Comp.

limit

max

9.12 10.98 13.08 14.61 15.99 17.52 18.51

TRE

method

CR 6.35 8.02 9.71 10.99 12.14 13.37 14.20

Proposed

method

CR 8.95 10.75 12.82 14.31 15.68 17.19 18.17

As was said above, several symbols with null

probability can be noticed in the runs of zeros his-

togram, meanwhile other symbols are clearly more

frequent than any other. In the TRE method, same

length codewords are used for every symbol, but it

does not take advantage of the different symbols pro-

babilities. As a result, ﬁgure 4 shows that the com-

pression ratios derived with this technique are signiﬁ-

cantly lower than the maximum ones. On the other

hand, the proposed compression scheme takes ad-

vantage of the different probabilities through a Huff-

man encoder. Thus shorter codewords are assigned to

more probable symbols so the expected length of the

generated code decreases and consequently the com-

pression performance improves. In this way we ob-

tain CR values closer to the upper bounds.

2 2.5 3 3.5 4 4.5 5 5.5

PRD

Compression limit

Proposed method

TRE method

Figure 4: Compression comparative study results.

6 CONCLUSIONS

In this work a thresholding-based compression

scheme using DWT is proposed. The results show

a better performance than similar compressors in the

state of the art. The entropy analysis of the indepen-

dent symbols used to encode is carried out and the

upper compression ratio bound is derived. The CR

max

calculation is revealed as an effective tool to evalu-

ate the compression bound that a speciﬁc scheme can

provide. In this work, the TRE method has been

analyzed as it has demonstrated good performance

among those in its category. The analysis of the upper

CR bound tells us that there is still a gap for the im-

provement. Therefore, a Huffman encoder (Skretting,

1999) is applied as source coder attaining better re-

sults for a wide range of PRD values. The obtained

CR values keep very close to the upper bound. There-

fore, an optimal result has been obtained for this par-

ticular scheme.

ACKNOWLEDGEMENTS

This work has been supported in part by Grant PR-

2007-0216 from the Ministerio de Educaci´on y Cien-

cia, in part by the Fondo de Investigaci´on San-

itaria under Project PI052277, in part by Comu-

nidad Aut´onoma de Madrid and Universidad de Al-

cal´a through project CCG07-UAH/TIC-2034, in part

by the Fundaci´on de Investigaci´on M´edica Mutua

EFFICIENT SOURCE CODING IN A THRESHOLDING-BASED ECG COMPRESSOR USING THE DISCRETE

WAVELET TRANSFORM

263

Madrile˜na and in part by grant “Introducci´on a la In-

vestigaci´on” from Universidad de Alcal´a held by Car-

los Hernando–Ramiro.

REFERENCES

Abo-Zahhad, M. and Rajoub, B. A. (2002). An

effective coding technique for the compression of

one–dimesional signals using wavelet transforms.

Medical Engineering and Physics, 24(3):185–199.

Benzid, R., Marir, F., and Bouguechal, N.-E. (2007).

Electrocardiogram compression method based on the

adaptative wavelet coefﬁcients quantization combined

to a modiﬁed two-roled encoder. IEEE Signal Pro-

cessing Letters, 14(6):373–376.

Benzid, R., Marir, F., Boussaad, A., Benyoucef, M.,

and Arar, D. (2003). Fixed percentage of wavelet

coefficients to be zeroed for ECG compression. Elec-

tronics Letters, 39(11):830–831.

Blanco Velasco, M., Cruz Rold´an, F., Godino Llorente,

J. I., and Barner, K. E. (2004a). ECG compression

with retrieved quality guaranteed. Electronics Letters,

40(23):1466–1467.

Blanco Velasco, M., Cruz Rold´an, F., Godino Llorente, J. I.,

and Barner, K. E. (2007). Wavelet packets feasibility

study for the design of an ECG compressor. IEEE

Trans. on Biomedical Signal Processing, 54(4):766–

769.

Blanco Velasco, M., Cruz Rold´an, F., L´opez Ferreras,

F.,

Angel Bravo Santos, and Mart´ınez Mu˜n´oz, D.

(2004b). A low computational complexity algorithm

for ECG signal compression. Medical Engineering

and Physics, 26(7):553–568.

Chen, J., Ma, J., Zhang, Y., and Shi, X. (2006). ECG com-

pression based on wavelet transform and Golomb cod-

ing. Medical Engineering and Physics, 42(6):830–

831.

Cover, T. M. and Thomas, J. A. (2006). Elements of Infor-

mation Theory. John Wiley & Sons, New York, 2nd

edition.

Holter, N. J. (1961). New methods for heart studies. Sci-

ence, 134:1214–1220.

Skretting, K. (1999). Arithmetic Coding and

Huffman Coding in Matlab. (online)

http://www.ux.uis.no/∼karlsk/proj99.

Zigel, Y., Cohen, A., and Katz, A. (2000). The Weighted

Diagnostic Distortion (WDD) measure for ECG sig-

nal compression. IEEE Transactions on Biomedical

Engineering, 47(11):1422–1430.

BIOSIGNALS 2009 - International Conference on Bio-inspired Systems and Signal Processing

264