ECG SIMULATION WITH IMPROVED MODEL OF CELL ACTION
POTENTIALS
Roman Trobec, Matjaˇz Depolli and Viktor Avbelj
Department of communication systems, Joˇzef Stefan Institute, Jamova cesta 39, 1000 Ljubljana, Slovenia
Keywords:
ECG, action potential, repolarization, myocardium, computer simulation.
Abstract:
An improved model of action potentials (AP) is proposed to increase the accuracy of simulated electrocar-
diograms (ECGs). ECG simulator is based on a spatial model of a left ventricle, composed of cubic cells.
Three distinct APs, modeled with functions proposed by Wohlfard, have been assigned to the cells, forming
epicardial, mid, and endocardial layers. Identification of exact parameter values for AP models has been done
through optimization of the simulated ECGs. Results have shown that only through an introduction of a mi-
nor extension to the AP model, simulator is able to produce realistic ECGs. The same extension also proves
essential for achieving a good fit between the measured and modeled APs.
1 INTRODUCTION
The standard 12–lead electrocardiogram (ECG) is a
diagnostic tool in cardiology for more than 60 years.
It is a view on the electrical heart activity from the
body surface that results from differences between
potentials of myocardium cells. These in turn are
a consequence of different times in which cells ex-
cite (excitation sequence) and the differences in cells
themselves. The mechanisms for ECG generation are
still not fully understood. In our research, we tackle
the problem of ECG genesis on the cellular level,
more precisely, through the shape of the action po-
tentials (APs). Focus of this paper is on the shape of
the repolarization phase of modeled APs and on the
increase of its fidelity.
Modeling of APs on the cell level is quite com-
plex, because a system of non-linear time-dependant
differential equations has to be solved (Ten Tusscher
et al., 2004). Simpler method, proposed by Wohlfart
(Wohlfart, 1987), models APs as a product of two sig-
moidal functions (A andC) and one exponential func-
tion (B):
A(t) =
1
1+e
−k
1
t
B(t) = k
2
((1−k
3
)e
−k
4
t
+ k
3
)e
−k
5
t
C(t) =
1
1+e
k
6
(t−k
7
)
AP(t) = A(t) × B(t) ×C(t) ,
(1)
where component A(t) controls the initial upstroke
(phase 0), B(t) the immediate fast repolarization and
the AP plateau (phases 1 and 2, respectively), and
C(t) the repolarization part (phase 3). Because of the
characteristics of exponential functions, however, the
whole AP curve is influenced to some extent by all
the components.
A model of AP curve with four phases is shown
in Figure 1. Activation time (AT) represents delay be-
tween the myocardium excitation start and individual
cell activation, which is defined by the excitation se-
quence (both are shown on the spatial model in Figure
2). Repolarization time (RT) is a sum of AT and ac-
tion potential duration (APD) and is a measure of the
delay between the myocardium excitation start and in-
dividual cell repolarization end.
The mechanisms forming the repolarization phase
of ECG are still under investigations. For example,
the shape of the T wave, its width and its slopes have
not been elucidated yet in all details. Even more mys-
terious is the genesis of the U wave (Surawicz, 1998).
Figure 1: An example of AP with corresponding phases 0 –
4. AT, APD, and RT are shown at 90% repolarization.
18
Trobec R., Depolli M. and Avbelj V. (2009).
ECG SIMULATION WITH IMPROVED MODEL OF CELL ACTION POTENTIALS.
In Proceedings of the International Conference on Health Informatics, pages 18-21
DOI: 10.5220/0001535400180021
Copyright
c
 SciTePress

Several hypotheses are frequently quoted: U wave
genesis is a consequence of the late repolarization of
Purkinje fibers (Watanabe, 1975); U wave is gener-
ated because of mechanoelectrical feedback (Franz,
1996); U wave is a residual of the late repolarization
of cells in mid-myocardium (Druin et al., 1995).
A new view of the mid-myocardium hypothesis
was presented in (Ritsema van Eck et al., 2005) that
suggests that the end of the T wave is taken as the
residual of cancellation of opposing potential contri-
butions throughout the myocardium during the repo-
larization while the U wave arises because of imbal-
ance of potentials in the late repolarization because of
the prolongated repolarization of mid-myocardium.
Recently, it was shown that there are other alterna-
tives for T and U wave genesis (Depolli et al., 2008).
U waves can be generated even if the repolarization
of the mid-myocardium is not prolongated.
Leaving physiological causes aside and looking
on the problem purely mathematically, we experi-
enced drawbacks of the Wohlfart’s AP model in two
ways. First, we were unable to get a good fit between
the Wohlfart model and the measured APs from the
intact heart. Second, we identified the inability to
control AP phases 2 and 3 independently, to be the
limiting factor in our simulator’s abilities to produce
properly shaped ECGs. This comes about because the
slopes in these phases determine the shape and du-
ration of the T wave and the time of its appearance.
We propose an extension of the Wohlfart model in
terms of changing the repolarization part C(t) in the
Equation 1, as a solution for the problems mentioned
above.
The rest of the paper is organized as follows. In
Methods, the spatial model of the left ventricle and
the simulation procedure are described. The simu-
lation results obtained with the Wohlfart model are
compared with a measured ECG. In section 3, the pro-
posed model extension is introduced together with an
example of an improved AP curve fit and measured
ECG fidelity. The paper concludes with an overview
of the obtained results and further work.
2 METHODS
2.1 Model of the Left Ventricle
We constructed a three-dimensional model from
65628 cubic cells with a volume of 1 mm
3
, stylized
in a cup-like shape, shown in Figure 2. The model
is onion-like composition of twelve layers, which en-
ables different APs to be assigned to each layer. Re-
sults presented in this paper were obtained by com-
posing three thicker layers: epi, mid and endo, each
of them composed of four identical thinner layers.
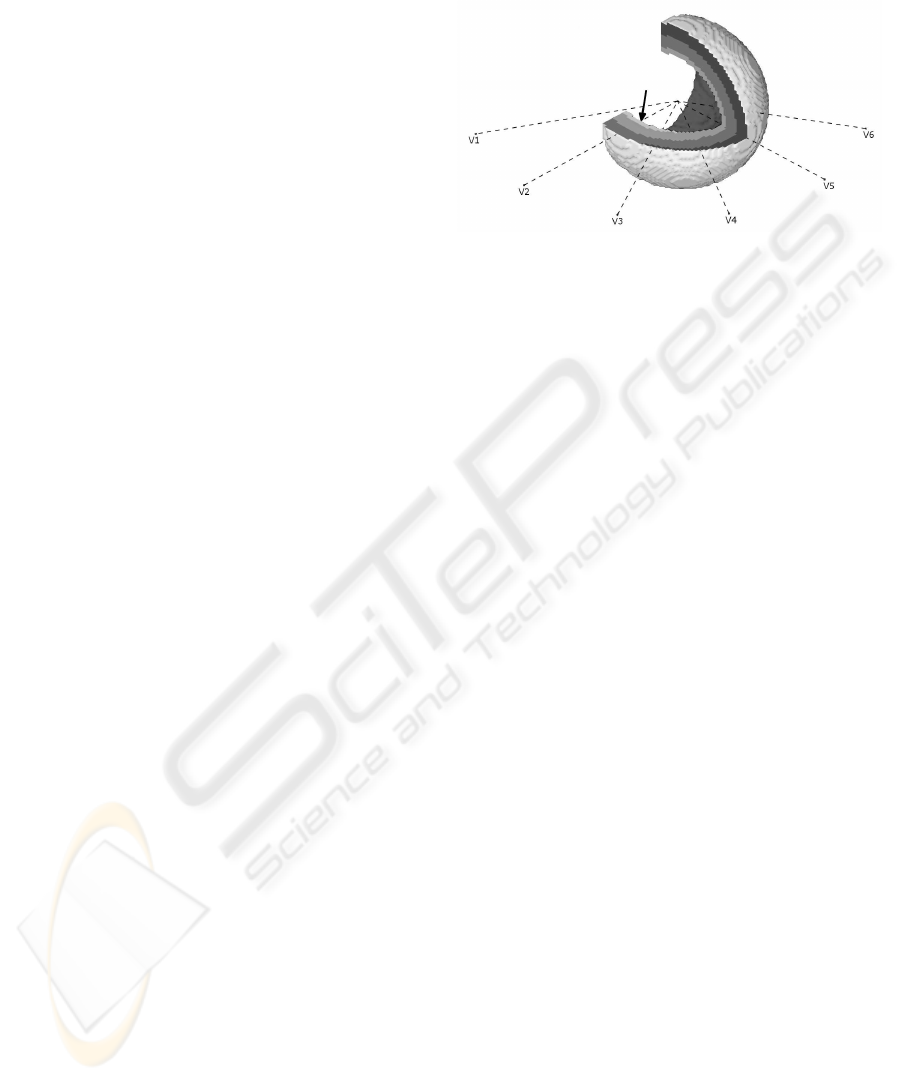
Figure 2: Spatial model of the left ventricle. ECG lead po-
sitions are shown with dashed lines. Arrow points to the
excitation trigger area. The excitation time is shown on the
cutout of the myocardial wall; each level of gray represent-
ing 10 ms.
Implementation of faster longitudinal conduction
between cells of the same layer (along the wall) than
transversal conduction between cells of different lay-
ers (across the wall) emulates faster conduction paths
of the Purkinje fibers .
2.2 Simulation Method
ECG is simulated by fist calculating the excitation se-
quence for all the cells and then projecting the sum of
differences in cell potentials on approximate positions
of ECG leads. Simulation procedure is integrated
into a simulator, that takes parameters of Equation 1
as input and generates ECGs on predefined positions
as output. This simulator is then used in simulation
based optimization that solves the inverse problem of
identification of AP parameters.
The ECG simulator works with cell APs and a
simple rule for each cell. Excited cells behave as
sources of electrical potential determined by their AP
functions. Every excited cell stimulates its neighbor-
ing non-excited cells to become excited with a small
delay, which depends on the layer of the neighboring
cell and its position relative to the excited cell. Be-
cause of the onion-like layering, cell neighbors along
the wall will be of the same layer while neighbors per-
pendicular to the wall will be of different layers. If
neighbors are from different layers, the delay of 2 ms
results in transversal conduction velocity of 0.5 m/s.
On the other hand, if neighbors belong to the same
layer, the delay of 1/3 ms results in longitudinal con-
duction velocity of 3 m/s. Both velocities are in ac-
cordance with measured values on myocardial tissue
(Macfarlane and Lawrie, 1989).
Six observation points were selected around the
model, 4 cm away from the epicardial layer, at an-
ECG SIMULATION WITH IMPROVED MODEL OF CELL ACTION POTENTIALS
19

gles −120° (V1) to 30° (V6), in increments of 30°,
as in a real ECG precordial leads placing (see Figure
2). For each observation point, an ECG is simulated
with the following procedure. We assume formation
of a dipole between cell i and its immediate neighbor-
hood Ω (caused by cells having different prescribed
APs and different ATs), in the same way as in (Miller
and Geselowitz, 1978). This includes only neighbors
with coincident faces, i.e., 6 neighbors for the spatial
model. Dipole moment D
i
is proportional to the vec-
tor sum of differences in potentials V:
D
i
(t) ∝
∑
j∈Ω(i)
(V
i
(t) −V
j
(t)) . (2)
ECG leads are simulated as a sum of dipole potential
contributions at the observation point P from all N
cells:
V
P
(t) ∝
N
∑
i=1
|D
i
(t)| · cosφ
|R
i,P
|
2
, (3)
where R
i,P
is a directional vector from the cell i to P,
and φ is the angle between D
i
and R
i,P
.
Simulator based optimization with evolutionary
algorithm works on top of the above simulation pro-
cedure. It deduces optimal parameters for three AP
groups from a predefined target ECG on a predefined
location. Currently, a measured ECG on V2 is used
as the target. The evaluation algorithm starts with a
number of random inputs for the simulator and gen-
erates ECGs on target location for each input. Then
it combines and modifies inputs in an evolution-like
procedure, resulting in inputs that produce ECGs very
similar to target ECG. Finally, the result of the opti-
mization is the input that produces the most similar
ECG.
2.3 Simulation Results – Wohlfart AP
Model
APs for epicardium, mid, and endocardium have been
generated with Wohlfart model, using coefficients
from Table 1. Resulting APs are shown in the up-
per part of Figure 3. The repolarization phase of the
simulated and measured ECGs onV
2
are shown in the
lower part of Figure 3. The simulated ECG fits well
the measured signal, however, some details around
the T and U waves are still inadequate.
Table 1: Coefficients of Equation 1 used for modeling APs
from Figure 3.
layer k
1
k
2
k
3
k
4
k
5
k
6
k
7
endo 2.5 100 0.9 0.1 0.00194 0.0755 326
mid 2.5 100 0.9 0.1 0.00260 0.0345 339
epi 2.5 100 0.9 0.1 0.00228 0.0376 296
0 100 200 300 400 500 600
ms
endo
mid
epi
0 100 200 300 400 500 600
ms
measured V2
simulated V2
Figure 3: Wohlfart APs for epicardial, mid and endocar-
dial layer (top), simulated and measured ECG repolariza-
tion phase on the lead V
2
(bottom). Note that the ECG on
the lower part of the figure is generated through Equation
3, where besides the APs (upper part of the figure), also the
shape of the heart model plays an important role.
3 MODIFIED AP MODEL
In the Wohlfart model, used in the previous section,
AP phases 2 and 3, and the transition between them
cannot be independently controlled. Shape of the
transition between phases 2 and 3 is defined by the
shape of the transition between phases 3 and 4, and
to some extent by the shape of phase 2. This depen-
dence constraints possible shapes of resulting T and
U waves and consequently limits the usability of our
simulator. Therefore, we propose a modification of
the factor C(t), which controls the repolarization part
of the ECG. Instead of using a simple sigmoid we in-
troduce an asymmetric sigmoidal function, which re-
quires an additional parameter k
8
:
C(t) = 1 − (1+ e
−k
6
(t−k
7
)+ln(2
k
6
k
8
−1)
)
−k
8
k
6
(4)
Incorporating the extended AP model, the simu-
lator immediately shows improvements. The results
of simulation based optimization on the same target
ECG as before are shown on Figure 4. The ECG fi-
delity is increased while the APs remain similar to
previous ones. The newly introduced asymmetry of
their phase 3 is barely noticeable.
The confirmation that proposed modification of
the AP model does not reflect a quirk of our simu-
lator but is an actual improvement of the model can
be found through examination of the measured APs.
Trying to fit both modified and unmodified Wohlfart
AP model (searching for parameters that would re-
sult in the most similar shape) to measured APs pub-
lished by Druin et al. (Druin et al., 1995), difference
HEALTHINF 2009 - International Conference on Health Informatics
20

0 100 200 300 400 500 600
ms
endo
mid
epi
0 100 200 300 400 500 600
ms
measured V2
simulated V2
Figure 4: Extended Wohlfart APs for epicardial, mid and
endocardial layer (top), simulated and measured ECG repo-
larization phase on the lead V
2
(bottom).
in model fidelity can be observed. An example is
shown in Figure 5, where the modified model, using
coefficients (1.0, 145.6, 0.8, 0.374, 0.00130, 0.0160,
0.244, 225) for k
1
to k
8
, respectively, fits the target
AP more accurately than does the unmodified model.
Both models were fitted to measured APs using the
same optimization method, based on an evolutionary
algorithm.
4 CONCLUSIONS
We have created a simple three-dimensional model of
a left ventricle for a computer simulation of ECGs.
The simulation is based on a variety of different AP
sets based on the Wohlfart AP model, which were
shown to have some limitations in the simulation of
known phenomena in the myocardial wall. Examin-
ing the AP model closer, problem with its fidelity was
discovered and identified as the most probable cause
of the mentioned simulator limitations. The problem
was solved through addition of another degree of free-
dom to the AP model.
We are preparing new simulations of ECGs with
the modified AP model and improvements of the op-
0 100 200 300
Druin et al.
Wohlfart
Modified
Figure 5: Endo AP published by Druin et al. (Druin et al.,
1995) (solid line), fitted with the Wohlfart model (dotted
line) and proposed modified model (dashed line).
timization. Currently, only one ECG lead can be tar-
geted at a time, which leads to inaccuracies of other
ECG leads. Although the modified AP model both in-
creases fidelity of simulated ECGs and enables better
approximation of measured APs, there are still dif-
ferences between measured APs and APs acquired
through our simulation based optimization. If we
succeed in reconciling these differences, we expect
that the simulator will provide helpful in explaining
some of the complex phenomena of the repolarization
phase.
ACKNOWLEDGEMENTS
The authors acknowledge financial support from the
Slovenian Research Agency under grant P2-0095.
REFERENCES
Depolli, M., Avbelj, V., and Trobec, V. (2008). Computer-
simulated alternative modes of U-wave genesis. J
Cardiovasc Electrophysiol, 19(1):84–89.
Druin, E., Charpentier, F., Gauthier, C., Laurent, K., and
Le Marec, H. (1995). Electrophysiologic characteris-
tics of cells spanning the left ventricular wall of hu-
man heart: Evidence for presence of M cells. J Am
Coll Cardiol, 26(1):185–192.
Franz, M. (1996). Mechano-electrical feedback in ventric-
ular myocardium. Cardiovasc Res, 32(1):15–24.
Macfarlane, P. and Lawrie, T., editors (1989). Compre-
hensive Electrocardiology: Theory and Practice in
Health and Disease, volume 1. Pergamon Press, New
York, 1st edition.
Miller, W. and Geselowitz, D. (1978). Simulation studies of
the electrocardiogram. I. The normal heart. Circ Res,
43(2):301–315.
Ritsema van Eck, H., Kors, J., and van Herpen, G. (2005).
The U wave in the electrocardiogram: A solution for a
100-year-old riddle. Cardiovasc Res, 67(2):256–262.
Surawicz, B. (1998). U wave: Facts, hypotheses, miscon-
ceptions, and misnomers. J Cardiovasc Electrophys-
iol, 9(10):1117–1128.
Ten Tusscher, K., Noble, D., Noble, P., and Panfilov, A.
(2004). A model for human ventricular tissue. Am J
Physiol Heart Circ Physiol, 286(4):H1573–H1589.
Watanabe, Y. (1975). Purkinje repolarization as a possible
cause of the U wave in the electrocardiogram. Circu-
lation, 51(6):1030–1037.
Wohlfart, B. (1987). A simple model for demonstration of
SST-changes in ECG. Eur Heart J, 8:409–416.
ECG SIMULATION WITH IMPROVED MODEL OF CELL ACTION POTENTIALS
21