
A COMPUTATIONAL SALIENCY MODEL INTEGRATING
SACCADE PROGRAMMING
Tien Ho-Phuoc, Anne Gu´erin-Dugu´e and Nathalie Guyader
GIPSA-lab/Department of Images and Signals, 961 rue de la Houille Blanche, F - 38402 Saint Martin d’H`eres cedex, France
Keywords:
Saccade programming, Saliency map, Spatially variant retinal resolution.
Abstract:
Saliency models have showed the ability of predicting where human eyes fixate when looking at images.
However, few models are interested in saccade programming strategies. We proposed a biologically-inspired
model to compute image saliency maps. Based on these saliency maps, we compared three different saccade
programming models depending on the number of programmed saccades. The results showed that the strategy
of programming one saccade at a time from the foveated point best matches the experimental data from free
viewing of natural images. Because saccade programming models depend on the foveated point where the
image is viewed at the highest resolution, we took into account the spatially variant retinal resolution. We
showed that the predicted eye fixations were more effective when this retinal resolution was combined with
the saccade programming strategies.
1 INTRODUCTION
Eye movement is a fundamental part of human vi-
sion for scene perception. People do not look at all
objects at the same time in the visual field but se-
quentially concentrate on attractive regions. Visual
information is acquired from these regions when the
eyes are stabilized (Egeth and Yantis, 1997; Hender-
son, 2003). Psychophysical experiments with eye-
trackers provide experimental data for both behav-
ioral and computational models to predict the attrac-
tive regions.
Computational models are in general divided into
two groups: task-independent models (bottom-up)
and task-dependent models (top-down). Most mod-
els describe bottom-up influences to create a saliency
map for gaze prediction. They areinspired by the con-
cept of the Feature Integration Theory of Treisman
and Gelade (Treisman and Gelade, 1980) and by the
first model proposed by Koch and Ullman (Koch and
Ullman, 1985). The most popular bottom-up saliency
model was proposed by Itti (Itti et al., 1998).
Eye movement experimental data consists, in gen-
eral, of fixations and saccades. Most models were
usually evaluated with distribution of fixations rather
than distribution of saccade amplitudes (in this paper,
saccade distribution
will be used to refer to distribu-
tion of saccade amplitudes). In order to evaluate more
precisely human saccades, saliency prediction must
be included inside a spatio-temporal process, even if
we consider only a bottom-up visual saliency map
from low-level features based on still images. A ques-
tion can be asked: is visual saliency evaluated again
at each fixation, or not?
Some studies showed that the saccadic system can
simultaneously program two saccades to two different
spatial locations (McPeek et al., 2000). This means
that from one foveated point, the next two saccades
are programmed in parallel; this is called the
con-
current processing
of saccades. Moreover, another
study (McPeek et al., 1998) showed that when sub-
jects are explicitly instructed to make a saccade only
after the current information at the fovea has been
analyzed, they have difficulty using this strategy. In
this paper, we consider different saccade program-
ming strategies during free viewing of natural im-
ages and we answer the questions: Do subjects make
one saccade at a time, programming the next sac-
cade from the current foveated point? Or do sub-
jects program the next two saccades from the cur-
rent foveated point? To answer these questions, we
tested two different models depending on the corre-
sponding number of programmed saccades from one
foveated point (cf. section 2.4). These two mod-
els were compared with the baseline model in which
all fixations were predicted from the same foveated
point. The mechanism of saccade programming will
be discussed through our experimental results, as it is
still an open question.
Saccade programming models are greatly linked
57
Ho-Phuoc T., Guérin-Dugué A. and Guyader N. (2009).
A COMPUTATIONAL SALIENCY MODEL INTEGRATING SACCADE PROGRAMMING.
In Proceedings of the International Conference on Bio-inspired Systems and Signal Processing, pages 57-64
DOI: 10.5220/0001535500570064
Copyright
c
SciTePress
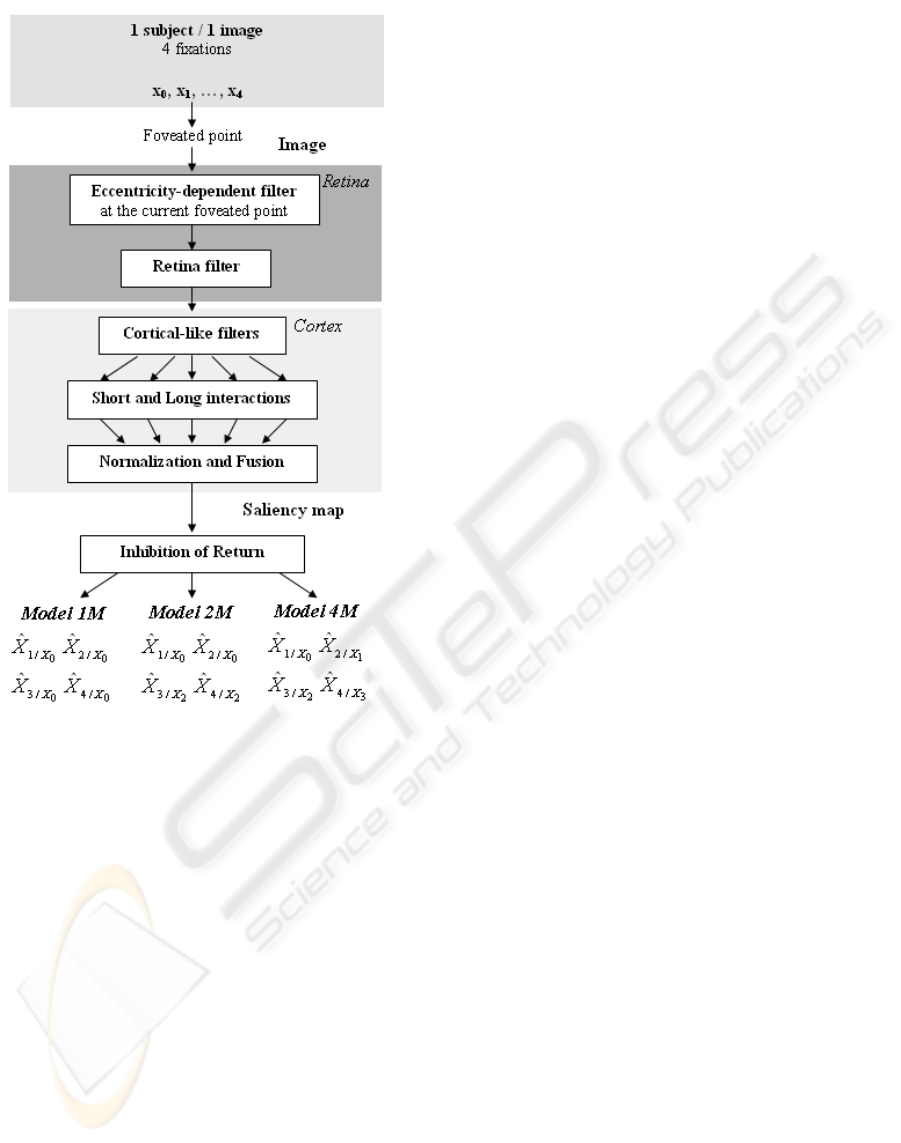
Figure 1: Functional description of the three saccade pro-
gramming models proposed.
to image resolution when it is projected on the retina.
The image on the fovea is viewed at higher resolu-
tion compared to the peripheral regions. This en-
hances the saliency of the region around the foveated
point. The spatial evolution of visual resolution is
one of the consequences of the non-uniform den-
sity of photoreceptors at retina level (Wandell, 1995).
When comparing experimental and predicted scan-
paths, Parkhurst (Parkhurst et al., 2002) noticed an
important bias on saccade distribution. The predicted
saccade distribution is quite uniform, contrary to the
experimental one where fixations are indeed located
on average near the foveated point. The decrease of
visual resolution on the peripheral regions contributes
to an explanation of this effect. In (Parkhurst et al.,
2002), this property was integrated in the model at
the final stage (multiplication of the saliency map by
a gaussian function).
In our model, we implement the decreasing den-
sity of photoreceptors as the first cause of this in-
homegeneous spatial representation. The output of
photoreceptors encodes spatial resolution depending
on eccentricity, given a parameter of resolution de-
cay (Geisler and Perry, 1998). While this parameter
influents low level retina processing, we intend to go
further in varying its value to mesure its impact on
high level visual processing, i.e. including the first
steps of the visual cortex. Similarly, in (Itti, 2006),
they noticed that the implementation of the spatially
variant retinal resolution improved the ability of fix-
ation prediction for dynamic stimuli (video games),
but the question of saccade programming was not ad-
dressed. Here, we show that this positive effect of
fixation prediction is even significant with static vi-
sual stimuli in combination with saccade program-
ming models.
Consequently, the proposed models are dynamic
ones as the high resolution regions, corresponding to
the fovea, change temporally according to the scan-
path. Three saccade programming strategies are ana-
lyzed. Experimental results show the interest of this
approachwith spatially variant retinal resolution. The
models are described in section 2. Section 3 presents
the experiment of free viewing to record eye fixations
and saccades, and the evaluationof the proposed mod-
els. Discussion is drawn in section 4.
2 DESCRIPTION OF THE
PROPOSED MODELS
Our biologically-inspired models (Fig. 1) consist of
one or more saliency maps in combination with sac-
cade programming strategies. The model integrates
the bottom-up pathway from low-level image prop-
erties through the retina and primary visual cortex to
predict salient areas. The retina filter plays an impor-
tant role: implementing non-linear response of pho-
toreceptors and then, spatially variant resolution. The
retinal image is then projected into a bank of cortical-
like filters (Gabor filters) which compete and interact,
to finally produce a saliency map. This map is then
used with a mechanism of “Inhibition of Return” to
create the saccade programming model. All these el-
ements are described below.
2.1 Retina Filter
In (Beaudot et al., 1993) the retina is modeled quite
completely according to its biological functions: spa-
tially variant retinal resolution, luminance adaptation
and contrastenhancement. These three characteristics
are taken into account while usually a simple modelis
BIOSIGNALS 2009 - International Conference on Bio-inspired Systems and Signal Processing
58

used such as a function of difference of Gaussians (Itti
et al., 1998).
Spatially variant retinal resolution
: Since the den-
sity of photoreceptors decreases as eccentricity from
the fovea increases(Wandell, 1995), the bluringeffect
increases from the fovea to the periphery and is re-
flected by an eccentricity-dependentfilter. The cut-off
frequency f
co
of this filter decreases with eccentricity
ecc expressed in degree (Fig. 2a). The variation of the
cut-off frequency (Eq. 1) is adapted from (Geisler and
Perry, 1998; Perry, 2002):
f
co
(ecc) = fmax
co
.
α
α+ |ecc|
, (1)
where α is the paramater controlling the resolution
decay, and fmax
co
the maximal cut-off frequency in
the fovea. Biological studies showed that α is close to
2.3
◦
(Perry, 2002). Figure 2b shows an example of an
image filtered spatially at the center with α = 2.3
◦
.
Luminance adaptation
: Photoreceptors adapt to a
varying range of luminance and increase luminancein
dark regionswithout saturation of luminance in bright
ones. They carry out a compression function (Eq. 2) :
y = y
max
.
x
x+ x
o
, (2)
where x is the luminance of the initial image, x
o
rep-
resents its average local luminance, y
max
a normaliza-
tion factor and y the photoreceptor output (Beaudot
et al., 1993).
Contrast enhancement
: The output of horizontal
cells, the low-pass response of photoreceptors, passes
throughbipolar cells and then, throughdifferent types
of ganglion cells: parvocellular, magnocellular and
koniocellular cells. We only consider the two princi-
pal cells: parvocellular and magnocellular. Parvocel-
lular cells are sensitive to high spatial frequency and
can be modeled by the difference between photore-
ceptors and horizontal cells. Therefore, they enhance
the initial image contrast and whiten its energy spec-
trum (Fig. 5b). Magnocellular cells respond to lower
spatial frequency and are modeled by a low-pass filter
like horizontal cells.
In human visual perception, we know that low fre-
quencies precede high frequencies (Navon, 1977). In
our model, we do not take into account this tempo-
ral aspect. However, as both low and high frequency
components are necessary for a saliency map, we
compute the retina output as a linear combination of
the parvocellularand magnocellular outputs (Fig. 5b).
(a) (b)
Figure 2: (a) Normalized cut-off frequency as function of
eccentricity for different values of α controlling the resolu-
tion decay. (b) An example of the output of the eccentricity-
dependent filter with α = 2.3
◦
, the foveated point is at the
image center (marked with the cross).
2.2 Cortical-Like Filters
2.2.1 Gabor Filters
Retinal image is transmitted to V1 which processes
signals in different frequencies, orientations, colors
and motion. We only consider the frequency and ori-
entation decomposition carried out by complex cells.
Among several works modeling responses of these
cells, Gabor filters are evaluated as good candidates.
A set of Gabor filters is implemented to cover all ori-
entations and spatial frequencies in the frequentialdo-
main. A filter G
i, j
(Eq. 3) is tuned to its central ra-
dial frequency f
j
at the orientation θ
i
. There are N
θ
orientations and N
f
radial frequencies (N
θ
= 8 and
N
f
= 4). The radial frequency is such as f
N
f
= 0.25
and f
j− 1
=
f
j
2
, j = N
f
,..,2. The standard deviations
of G
i, j
are σ
f
i, j
and σ
θ
i, j
in the radial direction and its
perpendicular one, respectively. σ
f
i, j
is chosen in such
a way that filters G
i, j
and G
i, j− 1
are tangent at level
of 0.5. We notice that the choice of the standard de-
viations influences the predicted saliency map. We
choose σ
f
i, j
= σ
θ
i, j
, which is justified in the next sec-
tion.
G
i, j
(u,v) = exp
(
−
(u
′
− f
j
)
2
2(σ
f
i, j
)
2
+
v
′2
2(σ
θ
i, j
)
2
!)
(3)
with:
u
′
= ucos(θ
i
) + vsin(θ
i
)
v
′
= vcos(θ
i
) − usin(θ
i
)
where u (respectively v) is the horizontal (respectively
vertical) spatial frequency. Then, for each channel,
complex cells are implemented as the square ampli-
tude of the Gabor filter output, providing the energy
maps e
i, j
.
A COMPUTATIONAL SALIENCY MODEL INTEGRATING SACCADE PROGRAMMING
59

Figure 3: Example of butterfly masks with different orien-
tations and scales.
2.2.2 Interaction between Filters
The responses of neurons in the primary visual cor-
tex are influenced in the manner of excitation or in-
hibition by other neurons. As these interactions be-
tween neurons are quite complex, we only consider
two types of interactions based on the range of recep-
tive fields (Hansen et al., 2001).
Short interactions are the interactions among neu-
rons having overlapping receptive fields. They occur
with the same pixel in different energy maps (Eq. 4):
m
s
i, j
= 0, 5.e
i, j− 1
+ e
i, j
+ 0,5.e
i, j+1
− 0,5.e
i+1, j
−0,5.e
i−1, j
. (4)
These interactions introduce inhibition between
neurons of neighboring orientations on the same
scale, and excitation between neurons of the same
orientation on neighboring scales. For the standard
deviations of the cortical-like filters, if σ
f
i, j
> σ
θ
i, j
the filters are more orientation-selective. However,
this choice reduces the inhibitive interaction. So, we
choose σ
f
i, j
= σ
θ
i, j
.
The second interactions are long interactions
which occur among colinear neurons of non-
overlapping receptive fields and are often used for
contour facilitation (Hansen et al., 2001). This inter-
action type is directly a convolution product on each
map m
s
i, j
to produce an intermediate map m
i, j
. The
convolution kernel is a “butterfly” mask b
i, j
(Fig. 3).
The orientation of the mask b
i, j
for the map m
s
i, j
is
the orientation θ
i
, and the mask size is inversely pro-
portional to the central radial frequency f
j
. The “but-
terfly” mask b
i, j
has two parts: an excitatory part b
+
i, j
in the preferential direction θ
i
and an inhibitive one
b
−
i, j
in all other directions. It is normalized in such
a way that its summation is set to 1. Figure 4 (first
row) shows the interaction effect for contour facilita-
tion (Fig. 4c).
(a) (b) (c)
(d) (e) (f)
Figure 4: Tests showing the influence of interaction and nor-
malization steps. The initial images are on the left column.
The corresponding saliency maps are on the center and right
column. First row, interaction effect: (a) Initial image; (b)
without interaction; (c) with interaction. Second row, nor-
malization effect: (d) Initial image; (e) without normaliza-
tion; (f) with normalization.
2.3 Normalization and Fusion
Intermediate maps m
i, j
must be normalized before
fusion. Moreover, an object is more salient if it is
different in comparison to its neighbors. We use
the method proposed by L. Itti (Itti et al., 1998) to
strengthen intermediate maps. Then, the maps are
thresholded. Figure 4 (second row) representsthe role
of the normalization step in reinforcing the filter out-
put where a Gabor patch is different from the back-
ground (Fig. 4f).
The normalization of each map is carried out as
follows:
• Normalize the intermediate map in [0, 1]
• Let us designate m
∗
i, j
the maximal value of map
m
i, j
and
m
i, j
its average. Then, the value at each
pixel is multiplied by (m
∗
i, j
−
m
i, j
)
2
.
• Set to zero all the values which are smaller than
20% of the maximal value.
Finally, all intermediate maps are summed up
in different orientations and frequencies to obtain a
saliency map. Examples of retinal image and saliency
map are given in Fig. 5.
2.4 Saccade Programming
Our models predict the first four fixations as an ex-
tension of the study in (McPeek et al., 2000) (two
BIOSIGNALS 2009 - International Conference on Bio-inspired Systems and Signal Processing
60

(a) Initial image (b) Retinal image
(c) Saliency map (d) Human fixations
Figure 5: Examples of retinal output, saliency map and hu-
man fixations for a part of an image used in the experiment.
saccades or two fixations). The fixations are pre-
dicted (and consequently the saccades) from the out-
put saliency map by implementing a simple mech-
anism of “Inhibition of Return” (IOR). We have
defined three saccade programming models, called
“1M”, “2M” and “4M” (Fig. 1). The “1M” model
has often been used with the hypothesis that all fixa-
tions can be predicted from the same foveated point
at the image center. Here, we tested two other models
where each foveated point allows the next or the next
two fixations to be predicted (“4M” or “2M”, respec-
tively). Let us explain first the IOR mechanism with
the “1M” model which is considered as the baseline
model. The first fixation is chosen as the pixel which
has the maximal value on the saliency map. Then, this
fixation becomes the foveated point to predict the sec-
ond saccade. Hence, the second fixation is chosen as
the pixel of maximal value after inhibiting the surface
around the foveated point (radius of 1
◦
). This mecha-
nism continues for the third and fourth fixations. For
the “2M” and “4M” models, the IOR mechanism is
applied in the same manner as for the “1M” model
except that the four fixations are predicted from more
than one saliency map (see below).
In the “1M” model, the eccentricity-dependentfil-
ter is applied only once to the center X
0
of images (be-
cause during the eye movement experiment, images
appeared only if subjects were looking at the center of
the screen). Then, a saliency map is computed from
this foveated point to predict four fixations
ˆ
X
1/X
0
,
ˆ
X
2/X
0
,
ˆ
X
3/X
0
,
ˆ
X
4/X
0
by using the IOR mechanism. For
the “2M” model, the eccentricity-dependent filter is
applied first to the center X
0
, as for the “1M” model,
to predict the first two fixations (on the first saliency
map)
ˆ
X
1/X
0
,
ˆ
X
2/X
0
; then, the eccentricity-dependent
filter is applied again to the second fixation for pre-
dicting the next two fixations (on the second saliency
map)
ˆ
X
3/X
2
,
ˆ
X
4/X
2
. Because the second fixation is dif-
ferent from one subject to another we take into ac-
count the second fixation X
2
of each subject for each
image. The “4M” model does the same by applying
the eccentricity-dependent filter and calculating the
saliency map for each fixation of each subject (four
saliency maps are sequentially evaluated).
3 EXPERIMENTAL EVALUATION
3.1 Eye Movement Experiment
We ran an experiment to obtain the eye scanpaths of
different subjects when they were looking freely at
different images. Figure 5d shows the fixations of all
subjects on a part of an image. The recording of eye
movements served as a method to evaluate our pro-
posed model of visual saliency and saccade program-
ming.
Participants
: Eleven human observers were asked
to look at images without any particular task. All par-
ticipants had normal or corrected to normal vision,
and were not aware of the purpose of the experiment.
Apparatus
: Eye tracking was performed by an
Eyelink II (SR Research). We used a binocular
recording of the pupils tracking at 500Hz. A 9-point
calibration was made before each experiment. The
velocity saccadic threshold is 30
◦
/ s and the acceler-
ation saccadic threshold is 8000
◦
/ s
2
.
Stimuli
: We chose 37 gray level images (1024×
768 pixels) with various contents (people, landscapes,
objects or manufactural images).
Procedure
: During the experiment, participants
were seated with their chin supported in front of a
21” color monitor (75 Hz refresh rate) at a viewing
distance of 57 cm (40
◦
× 30
◦
usable field of view).
An experiment consisted in the succession of three
items : a fixation cross in the center of the screen,
followed by an image during 1.5 s and a mean grey
level screen for 1 s. It is important to note that the
image appeared only if the subject was looking at the
fixation cross; we ensured the position of the eyes be-
fore the onset of images. Subjects saw the same 37
images in a random order.
We analyzed the fixations and saccades of the
guiding eye for each subject and each image.
A COMPUTATIONAL SALIENCY MODEL INTEGRATING SACCADE PROGRAMMING
61

3.2 Criterion Choice for Evaluation
The qualities of the model, moreprecisely the saccade
programming strategy and the eccentricity-dependent
filter, are evaluated with the experimental data (fixa-
tions and saccades). This evaluation allows to test the
predicted salient regions and the saccade distribution.
Firstly, the three models “1M”, “2M” and “4M”
are used to test saccade programming strategies. The
evaluation protocol as in (Torralba et al., 2006) is to
extract from a saliency map the most salient regions
representing 20% of the map surface. Let us call each
fixation “correct fixation” (respectively “incorrect fix-
ation”) if the fixation is inside (respectively outside)
these predicted salient regions. The ratio R
c
(i,s) of
“correct fixation” for an image i and a subject s is
given below:
R
c
(i,s) =
N
inside
N
all
.100, (5)
where N
inside
is the number of fixations inside the
salient regions and N
all
is the total number of fixa-
tions.
The average ratio of correct fixations of all cou-
ples (subject × image) is computed. Particularly for
each couple, in the “1M” model, one saliency map
is used to calculate correct fixation index for the first
four fixations. In the “2M” model, the first saliency
map is used for the first two fixations and the second
map for the next two fixations (Fig. 1). Similarly for
the “4M” model, each saliency map is used for the
corresponding fixation. It is noticed that in the “1M”
model, the saliency map of each image is identical for
all subjects (whose foveated point is always at the im-
age center). However, it is no longer the case for the
“2M” or “4M” model where a saliency map depends
on the foveated points of a subject.
Secondly, from the most suitable saccade pro-
gramming strategy chosen above, the predicted sac-
cade distribution for the first four saccades is com-
puted and compared with the emperical one from our
experimental data. It has been shown that the parame-
ter α (Eq. 1) which fits the experimental data based on
contrast threshold detection when presenting eccen-
tred gratings is around 2.3
◦
(Perry, 2002). Here, by
varying the α values, the expected effects are: (i) this
parameter must have a great influence on saccade dis-
tribution and (ii) the best value would be in the same
order of magnitude as 2.3
◦
.
3.3 Results
3.3.1 Evaluation of the Three Saccade
Programming Models
For saccade programming, Fig. 6 shows the criterion
of correct fixations R
c
as a function of fixation order
with five α values (0.5
◦
, 1
◦
, 2
◦
, 4
◦
and infinity) for
the three models. R
c
of the first fixation is identical
for these three models because of the same starting
foveated point. It is also the case for R
c
of the sec-
ond fixation in “1M” and “2M”, and R
c
of the third
fixation in “2M” and “4M”. R
c
for all three models
has the same global trend: decrease with fixation or-
der. The R
c
ratio is greater for the “4M” model in
comparison to the “1M” model for all fixations. It re-
sults from the reinitialization of the foveated point. In
the “2M” model, an intermediate of the two previous
ones, the increase of R
c
from the second to third fix-
ation is also explained by this reinitialization. More-
over, the decrease at the second and fourth fixation (in
“2M”) presents necessity of the reinitialization, but at
each fixation. The slower decrease of R
c
in “4M” is
also coherent with this interpretation.
The α parameter also influences the quality of the
predicted regions. Saliency models including spa-
tially variant retinal resolution give better results than
the model with constant resolution for the first four
fixations (t-test, p < 0.005, except the cases α = 0.5
◦
and α = 1
◦
for the third fixation). However, among
α = 0.5
◦
, α = 1
◦
, α = 2
◦
and α = 4
◦
there is no sig-
nificant difference except for the first fixation. At
this fixation, there is no difference between R
c
of
cases 0.5
◦
and 1
◦
but they are significantly greater
than those in cases 2
◦
and 4
◦
(F(3,1612) = 10.45,
p < 0.005).
3.3.2 Configuration of the
Eccentricity-Dependent Filter
To evaluate the influence of the spatially variant reti-
nal resolution on the saccade distribution, the same
five α values are tested with the “4M” model which
fits best the human fixations. We observe a great in-
fluence of α on saccade distribution. Figure7 presents
the experimental saccade distribution and those of the
“4M” model according to the five α values. The
distribution is very narrow with α = 0.5
◦
(Fig. 7b),
larger with greater α, and tends to a uniform dis-
tribution when α tends to infinity (Fig. 7f). The
effect of the spatially variant retinal resolution can
be shown through these distributions, concerning not
only the dispersion but also the position of the max-
imum mode. Let us consider only two characteris-
tics of the saccade distribution : form and position
BIOSIGNALS 2009 - International Conference on Bio-inspired Systems and Signal Processing
62
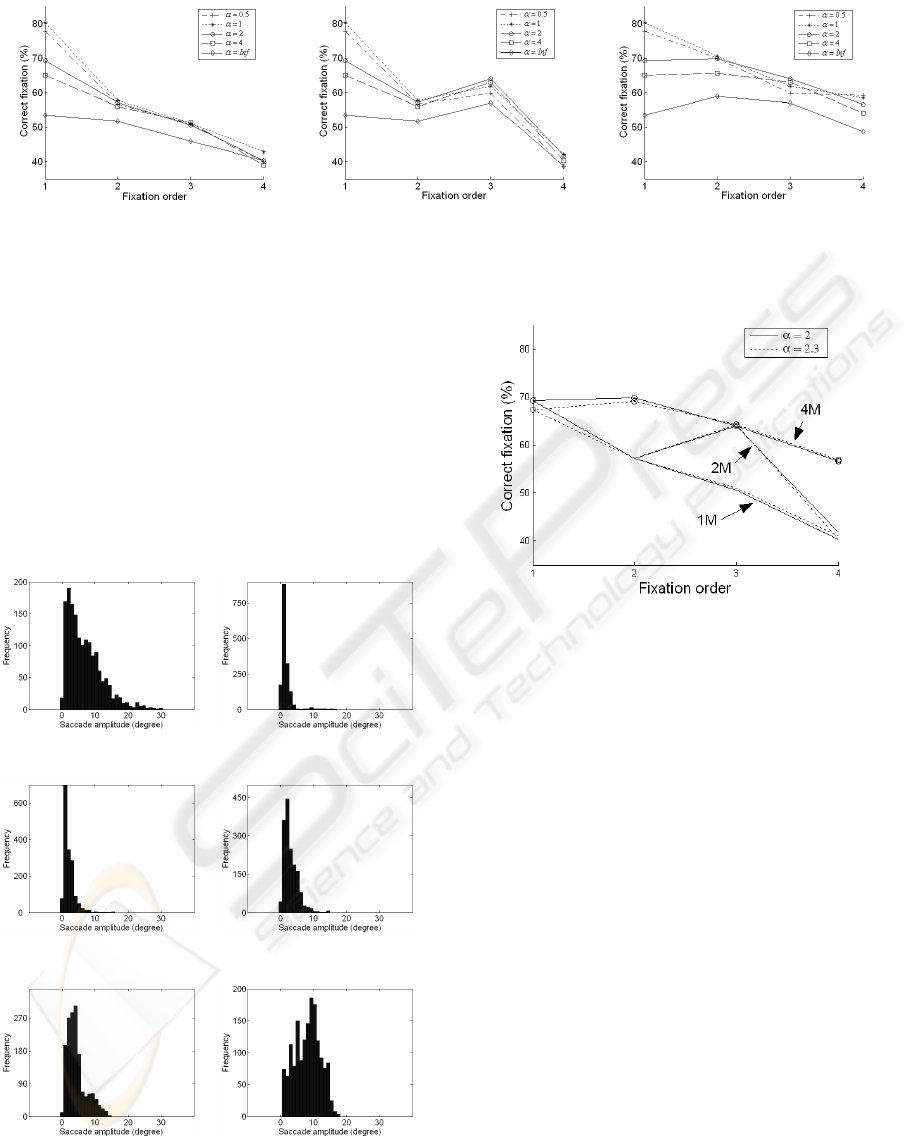
(a) “1M” (b) “2M” (c) “4M”
Figure 6: R
c
as a function of fixation order of the three models with different α values.
of the maximum mode. By varying α, we can adapt
either distribution form or mode position. However,
it is difficult to fit at the same time both form and
mode position just only by adjusting one parameter
(α here). Hence, the best parameter α is chosen as
the best qualitative compromise between the distribu-
tion form and mode position. Among these α val-
ues, according to the mode position, the distribution
with α = 2
◦
has the same mode position of about 2.1
◦
as the experimental distribution. This distribution de-
creases progressively while eccentricity increases.
(a) Human (b) “4M” with α = 0.5
◦
(c) “4M” with α = 1
◦
(d) “4M” with α = 2
◦
(e) “4M” with α = 4
◦
(f) “4M” with α = Inf
Figure 7: Saccade distribution of the experimental data and
the “4M” model according to different values of α.
Figure 8: Comparison of R
c
between α = 2
◦
and α = 2.3
◦
for the three models.
Indeed, when varying the α parameter, we notice
a continuous effect both on the ratio R
c
of “correct
fixation” and saccade distribution. The results from
the simulations with α = 2.3
◦
are very close to those
obtained with α = 2
◦
(Fig. 8). By lack of space, the
saccade distribution of the “4M” model for α = 2.3
◦
,
which is almost the same as for α = 2
◦
, is not shown.
4 DISCUSSION
Firstly, all three models have the ratio of correct fix-
ation decreasing according to the fixation order. This
fact can be explained by the influence of top-down
mechanisms which arise late and reduce the role of
bottom-up in visual attention. In reality, as time
passes, fixations of different subjects are more dis-
persive and subject-dependent. However, the influ-
ence of bottom-up still persists and the percentage of
correct fixations is much higher than by chance in all
three models. This confirms the role of bottom-up in
visual attention even with the increasing presence of
top-down.
The result of this study seems not to support pro-
A COMPUTATIONAL SALIENCY MODEL INTEGRATING SACCADE PROGRAMMING
63

gramming of several saccades in parallel. In fact,
we tested three models: the “1M” model program-
ming four saccades in parallel from the same foveated
point, the “2M” model programming two saccades in
parallel and the “4M” model programming only one
saccade at a time. This study showed that the “1M”
model is not realistic and the “4M” model seems to be
the most realistic. The behaviour of the “2M” model
illustrates that recomputing saliency in updating the
foveated point is beneficial. The best performance
comes however from the “4M” model presenting ef-
fectiveness of the reinitialization at each fixation. We
can conclude that saccade programming in parallel
seems not to be used by subjects when they have to
look freely at natural images.
Secondly, this study shows the positive effect of
the spatially variant retinal resolution on the pre-
diction quality. Whatever the saccade programming
strategy is, the models including the spatially vari-
ant retinal resolution greatly outperform the models
with constant resolution in terms of the quality of
fixation prediction and saccade distribution. The pa-
rameter α which controls the resolution decrease has
an important impact on saccade distribution (disper-
sion and mode position). Moreover, we found the
expected range of value for this parameter using our
model to compute saliency maps. We also notice that
if we have the same mode position, the dispersion of
the saccade distribution remains smaller on predicted
data than on experimental data, as we only consider a
bottom-up model and we have only one parameter to
adjust.
In our models, a foveated point for the next sac-
cade is selected from subjects’ fixations instead of be-
ing looked for in the present saliency map. While fix-
ations are different from one subject to another, the
model is a subject-dependent model. If we want to go
further in creating a more general model of predict-
ing eye movements automatically, the model would
take into account human task, for example catego-
rization or information search, and hence passes from
a region-predicting model to a scanpath-predicting
model.
ACKNOWLEDGEMENTS
This work is partially supported by grants from the
Rhˆone-Alpes Region with the LIMA project. T. Ho-
Phuoc’s PhD is funded by the French MESR.
REFERENCES
Beaudot, W., Palagi, P., and Herault, J. (1993). Realistic
simulation tool for early visual processing including
space, time and colour data. In International Work-
shop on Artificial Neural Networks, LNCS, volume
686, pages 370–375, Barcelona. Springer-Verlag.
Egeth, H. E. and Yantis, S. (1997). Visual attention: Con-
trol, representation, and time course. In Annual Re-
view of Psychology, volume 48, pages 269–297.
Geisler, W. S. and Perry, J. S. (1998). A real-time foveated
multiresolution system for low-bandwidth video com-
munication. In Human Vision and Electronic Imaging,
Proceedings of SPIE, volume 3299, pages 294–305.
Hansen, T., Sepp, W., and Neumann, H. (2001). Recurrent
long-range interactions in early vision. In S. Wermter,
J. A. and Willshaw, D., editors, Emergent Neural
Computational Architectures Based on Neuroscience,
LNCS/LNAI, volume 2036, pages 139–153.
Henderson, J. M. (2003). Human gaze control in real-world
scene perception. In Trends in Cognitive Sciences,
volume 7, pages 498–504.
Itti, L. (2006). Quantitative modeling of perceptual salience
at human eye position. In Visual Cognition, vol-
ume 14, pages 959–984.
Itti, L., Koch, C., and Niebur, E. (1998). A model of
saliency-based visual attention for rapid scene anal-
ysis. In IEEE Transactions on Pattern Analysis and
Machine Intelligence, volume 20, pages 1254–1259.
Koch, C. and Ullman, S. (1985). Shifts in selective visual
attention: towards the underlying neural circuitry. In
Human Neurobiology, volume 4, pages 219–227.
McPeek, R. M., Skavenski, A. A., and Nakayama, K.
(1998). Adjustment of fixation duration in visual
search. In Vision Research, volume 38, pages 1295–
1302.
McPeek, R. M., Skavenski, A. A., and Nakayama, K.
(2000). Concurrent processing of saccades in visual
search. In Vision Research, volume 40, pages 2499–
2516.
Navon, D. (1977). Forest before trees: the precedence of
global features in visual perception. In Cognitive Psy-
chology, volume 9, pages 353–383.
Parkhurst, D., Law, K., and Niebur, E. (2002). Modeling
the role of salience in the allocation of overt visual
attention. In Vision Research, volume 42, pages 107–
123.
Perry, J. S.(2002). http://fi.cvis.psy.utexas.edu/software.shtml.
Torralba, A., Oliva, A., Castelhano, M. S., and Henderson,
J. M. (2006). Contextual guidance of eye movements
and attention in real-world scenes: The role of global
features in object search. In Psychological Review,
volume 113, pages 766–786.
Treisman, A. and Gelade, G. (1980). A feature integra-
tion theory of attention. In Cognitive Psychology, vol-
ume 12, pages 97–136.
Wandell, B. A. (1995). Foundations of Vision. Stanford
University.
BIOSIGNALS 2009 - International Conference on Bio-inspired Systems and Signal Processing
64
