
IMPROVING CLASSIFICATION FOR BRAIN COMPUTER
INTERFACES USING TRANSITIONS AND A MOVING WINDOW
Ricardo Aler, In´es M. Galv´an and Jos´e M. Valls
Computer Science Department, Universidad Carlos III de Madrid, Avda. Universidad, 30, Legan´es, Spain
Keywords:
Brain Computer Interface, Machine learning.
Abstract:
The context of this paper is the brain-computer interface (BCI), and in particular the classification of signals
with machine learning methods. In this paper we intend to improve classification accuracy by taking advantage
of a feature of BCIs: instances run in sequences belonging to the same class. In that case, the classification
problem can be reformulated into two subproblems: detecting class transitions and determining the class for
sequences of instances between transitions. We detect a transition when the Euclidean distance between the
power spectra at two different times is larger than a threshold. To tackle the second problem, instances are
classified by taking into account, not just the prediction for that instance, but a moving window of predictions
for previous instances. Our results are competitive with those obtained in the BCI III competition.
1 INTRODUCTION
The context of this paper is the brain-computer in-
terface (BCI), a growing research field, that would
allow users to control computers and other devices
by means of brain signals (Curran and Stokes, 2003),
(Millan J del R and Gerstner, 2004) (G. Pfurtscheller
and Birbaumer, 2005), (Kubler and Muller, 2007).
One of the main problems of BCI is to accurately
decode individual brain signals. Machine Learning
techniques are typically applied here, by training clas-
sifiers with the brain signals of the user that is going
to use the interface (Dornhege et al., 2007). For in-
stance, a BCI can be trained to recognize three dif-
ferent classes corresponding to three different mental
states: left-hand motor imagery, right-hand motor im-
agery, and object rotation imagery.
Noisy weak signals and high variability between
same-user sessions
1
make the classification problem
difficult, resulting in many on-line classification er-
rors, frustated users, and low transfer (speed) rates
from the user to the computer. The transfer rate could
be increased if three or more classes are used. How-
ever, multi-class classification problems are more dif-
ficult than two-class ones.
1
This means that the classifier learned during one ses-
sion might not be accurate in the next session, even for the
same user.
In this paper we intend to improve classification
accuracy by taking advantageof a feature of BCIs: in-
stances run in sequences belonging to the same class
(for instance, right-hand motor imagery), followed by
a transition into a different class. Typically, the BCI
classification problem is tackled by trying to classify
the EEG signal at every instant in time. However,
given that classes run in sequences, the classification
problem can be reformulated into two subproblems:
• Detecting class transitions
• Determining the class for sequences of instances
between transitions.
The first problem can be approached in many dif-
ferent ways. In this paper we detect transitions by
computing the Euclidean distance between the power
spectra at two different times (samples) and signalling
a class transition when the distance is larger than a
threshold.
By detecting transitions, the accuracy of the sec-
ond problem (classification between transitions) can
also be improved in two ways. First, if the class of
the last sequence (before the transition) is known, that
class can be discarded after the transition, hence be-
coming a simpler N-1 class classification problem.
Also, sequences may contain many instances (de-
pending of the sampling rate), but only a few are nec-
essary to determine the class of the whole sequence.
This is actually no different than determining if a coin
65
Aler R., Galván I. and Valls J. (2009).
IMPROVING CLASSIFICATION FOR BRAIN COMPUTER INTERFACES USING TRANSITIONS AND A MOVING WINDOW.
In Proceedings of the International Conference on Bio-inspired Systems and Signal Processing, pages 65-71
DOI: 10.5220/0001535800650071
Copyright
c
SciTePress

is biased towards heads or tails, based on a small sam-
ple of coin tosses. We use a similar idea in this paper.
We have applied these ideas to the data supplied for
the BCI III competition. The datasets are described
in Section 2. The method is described in Section 3.
Section 4 shows the obtained results. Section 5 sum-
marizes our results and draws some conclusions.
2 DESCRIPTION OF EEG DATA
In this paper we are going to use a high quality dataset
acquired in the IDIAP Research Institute by Silvia
Chiappa and Jos del R. Milln (Mill´an, 2004). It was
used in the BCI-III competition that took place in
2005.
2
This dataset contains data from 3 normal sub-
jects during 4 non-feedback sessions. The subjects sat
in a normal chair, relaxed arms resting on their legs.
There are 3 tasks, so this is a three-class classification
problem:
• Imagination of repetitive self-paced left hand
movements
• Imagination of repetitive self-paced right hand
movements
• Generation of words beginning with the same ran-
dom letter
All 4 sessions of a given subject were acquired
on the same day, each lasting 4 minutes with 5-10
minutes breaks in between them. The subject per-
formed a given task for about 15 seconds and then
switched randomly to another task at the operator’s
request. EEG data is not splitted in trials since the
subjects are continuously performing any of the men-
tal tasks. Data was provided in two ways: raw EEG
signals, and data with precomputed features. In this
paper, we use the precomputed dataset.
Features were precomputed as follows. The raw
EEG potentials were first spatially filtered by means
of a surface Laplacian. Then, every 62.5 ms (i.e., 16
times per second) the power spectral density (PSD)
in the band 8-30 Hz was estimated over the last sec-
ond of data with a frequency resolution of 2 Hz for
the 8 centro-parietal channels C3, Cz, C4, CP1, CP2,
P3, Pz, and P4. As a result, an EEG sample is a 96-
dimensional vector (8 channels times 12 frequency
components).
In summary, in this paper we are going to tackle
a three-class classification problem with 96 input at-
tributes, which define the PSD over 62.5 ms for 8
input channels. There are three subjects, with four
2
http : //ida. first. fraunhofer.de/projects
/bci/competition iii/.
datasets (sessions) for each one: three datasets for
training and one dataset for testing.
3 METHOD
The method used here to improve BCI classification
accuracy based on assigning a class to a complete se-
quence of instances is based on two main ideas. First,
the transition in the signal from a class to another
class must be detected. This knowledge is used to
discard the class assigned to the previous sequence
of instances, just before the transition. Hence, the
prediction problem of N classes is transformed into a
prediction problem of N − 1 classes. Usually, in clas-
sification tasks the reduction of the number of classes
helps to increase the performance of the classification
algorithm.
On the other hand, the proposed method is in-
spired in the idea that in this problem, the class
to predict remains fixed for a time period that we
havecalled sequence of instances between transitions.
That means that, within a sequence, the class is not
continuously changing. Hence, it makes sense to try
to guess the class assigned to that sequence instead
of using the classifier to predict each instance of the
sequence independently of each other. The simplest
way to assign a class to a sequence is to compute the
majority class returned by the classifier on a small set
of instances at the beginning of the sequence. How-
ever, if the classifier makes many mistakes at the be-
ginning of the sequence, the whole sequence will be
missclassified. In our first approach, we tried to as-
sign a class to whole sequences based only on the first
instances, and very frequently, complete sequences
were missclassified, and the whole method crashed.
Therefore, we have decided to classify the i
′
th in-
stance in the sequence by considering a moving win-
dow of the n previous instances. This gives some in-
ertia to the classifier (it considers n instances instead
of just one), but if mistakes are made by the user,
the classifier will recover eventually, once the mov-
ing window has gone past the mistaken instances. We
offer a well-founded method for selecting the window
size n, that it is explained at the end of the section.
Next, a detailed description of the method is pre-
sented. It includes the following parts: the procedure
to detect the transition; the procedure to select the
classifier once the transition is detected and one of
the class is discarded; the procedure to classify test
instances with a moving window; and the mechanism
to compute the window size.
As we described in Section 2, we assume that the
original data in the time domain has been transformed
BIOSIGNALS 2009 - International Conference on Bio-inspired Systems and Signal Processing
66

to Power Spectral Density (PSD) in the frequency do-
main. Thus, we assume that we have a set of samples
(or instances) and every sample contains all the com-
ponents of the PSD for all channels at every instant.
That is:
sample
i
=
PSD
r, j
(i) j = 1,...,NoC, r = 1,...R
(1)
where PSD
r, j
(i) is the value of the r
th
spectral com-
ponent for the the j
th
channel, NoC is the number
of channels, and R is the number of components in
the PSD. For instance, if the PSD ranges from 8Hz
to 30Hz and there is a component every 2Hz (a 2Hz
resolution), R = 12.
Next, we describe the components of our method:
• Transition Detection. It is based on the observa-
tion that when a change of class occurs, a change
in the frequency domain also occurs. The idea
is to detect that transition by computing the Eu-
clidean distance between PSDs at two consecu-
tive samples. For every sample i, the distance
d
i
= ||PSD(i) − PSD(i− 1)|| between the PSD of
sample
i
and sample
i−1
is calculated as:
d
i
=
Noc
∑
j=1
R
∑
r=1
|PSD
r, j
(i) − PSD
r, j
(i− 1)|
(2)
Once the distance d
i
is obtained, a threshold value
U has to be set, such that if the distance is higher
that this threshold, a transition is signaled. The
value of U is crucial for successfully predict tran-
sitions and therefore, very important for the suc-
cess of the method.
In order to determine that threshold, the follow-
ing mechanism is applied. The training data set
X is divided into two subsets, named X
notransition
and X
transition
. The first one, X
notransition
, con-
tains the samples for which there is no tran-
sition; and, the second one X
transition
contains
the transition samples. This separation can be
made because samples are labeled in the train-
ing set (i.e. their class is known), and there-
fore a transition is just a change of class. After
that, the distances d
i
for samples in X
notransition
are calculated and the maximum of these dis-
tances, named MaxDis
notransition
, is also obtained
. The distances d
i
for samples in subset X
transition
are also obtained and ranked from low to high.
Obviously, a good threshold U must be larger
than MaxDis
notransition
. We currently define U
as the next d
i
of set X
transition
that is larger than
MaxDis
notransition
. This way of setting the thresh-
old does not guarantee that all transitions will be
detected. However, this method is simple and rea-
sonable and later we will show that it performs
correctly on the test data.
• Choosing the Appropriate Classifier, once the
Transition has been Detected. Let us remem-
ber that when a transition is detected, the class
of the previous sequence of instances is discarded
(i.e. after the transition, the class must change).
Therefore, after the transition, the system only
needs a classifier that is able to classify sam-
ples (or instances) into N − 1 classes (discarding
the previous class). As the system must be pre-
pared for all classes, all (N − 1)-class classifiers
must be trained off-line using the training data,
prior to the system going on-line. If there are
N classes (C
1
to C
N
), there will be N (N − 1)-
class classifiers. The first classifier, named K
2,...,N
,
assumes that class C
1
is discarded and will pre-
dict the class in the set {C
2
,...,C
N
}. The sec-
ond classifier, named K
1,3,...,N
, will discard class
C
2
and classify instances in N − 1 classes in the
set {C
1
,C
3
,... ,C
N
}. The k
′
th classifier, named
K
1,...k−1,k−1,...,N
, will consider only classes in the
set {C
1
,... ,C
k−1
,C
k+1
,...,C
N
}. And so on, until
{C
1
,...,C
N−1
}. Also, an N-class classifier must be
learned, because at the beginning there is no pre-
vious sequence of samples, and therefore, no class
can be discarded. In this work, we have used Sup-
port Vector Machines (SVM) because they obtain
a very good performance(Vapnik,1998), although
any other machine learning algorithm could have
been employed.
3
The method is applied to predict the class in real
time (on-line). The main idea is to use one of
the classifiers for N − 1 classes, when a transition
is detected, instead of using the general classifier
(the classifier for N classes). Usually, the perfor-
mance of classifiers with fewer classes is higher
because if a class is removed, uncertainty about
the class is also reduced.
The procedure to select the classifier in real-time
is described next: when the prediction process be-
gins, the N-class classifier is responsible for pre-
diction. At the same time, the distances d
i
given
by equation 2 are calculated. When a transition
occurs (i.e. d
i
> U), one of the N classifiers for
N − 1 classes must be chosen. To choose the
most appropriate classifier, the majority class pre-
dicted in the previous sequence of instances (i.e.,
the set of instances between the last two transi-
tions) must be discarded. Let’s suppose that the
3
In fact, we use Weka’s SMO implementation with stan-
dard parameters (a linear kernel and C = 1(Garner, 1995).
IMPROVING CLASSIFICATION FOR BRAIN COMPUTER INTERFACES USING TRANSITIONS AND A MOVING
WINDOW
67
class of the last sequence was k. Therefore, class
k will be ruled out for the current transition, and
the K
1,...k−1,k−1,...,N
classifier will be responsible
for prediction during the current sequence until
the next transition is detected.
• Procedure to Classify Test Instances with a
Moving Window
As explained at the beginning of the section, we
use a second idea here to improve classification
accuracy: in order to classify sample
i
, a window
with the predictions of the selected classifier for
the n previous samples will be used, instead of
just using the prediction for sample
i
. This is sim-
ilar to determining if a biased coin is biased to-
wards heads based only on the n previousfew coin
tosses. Sample
i
will be classified as the major-
ity class of instances within the window. It is a
moving window because only the last n predic-
tions just before sample
i
are taken into account.
As the windows moves, all the samples inside it
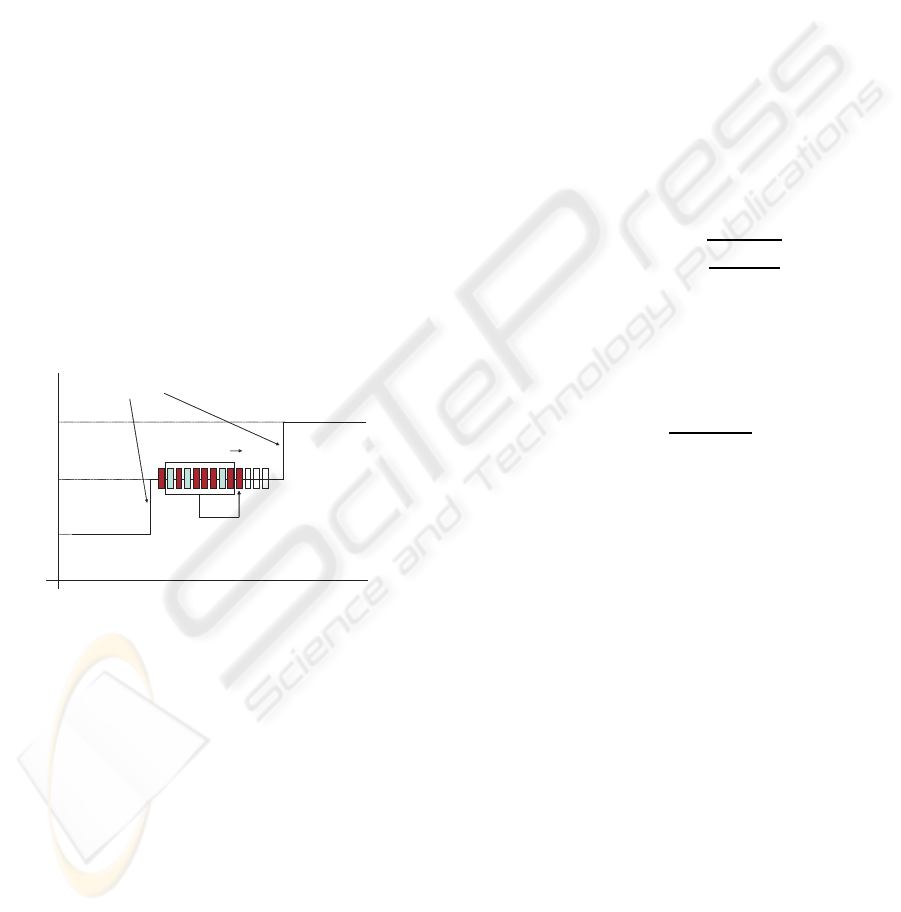
are classified by the selected classifier. Figure 1
shows how it works. The only remaining issue is
to estimate a ”good” window size n. This will be
done next.
Transitions
Class
Time
Movingwindow
Predictedinstance
Classa
Classb
Classc
......
ClassifierK
ac
ClassifierK
bc
ClassifierK
abc
Figure 1: Moving window to classify test instances.
• Computing the Size of the Moving Window
Assigning the majority class of instances within
the window to the next sample is reasonable, but
mistakes would occur if the frequencyof that class
in the window is not too far from 50%. This can
be solved by establishing a safe confidence in-
terval around the estimated frequency. For sim-
plification purposes, let’s suppose there are only
three classes (N = 3, classes a, b, and c), and as
explained before, one of them will be discarded
after the transition and one of the 3 2-class clas-
sifiers will be used for the current sequence un-
til the next transition. Let’s suppose that class a
is discarded and therefore classifier K
bc
must be
used for the current sequence (K
bc
separates class
b from class c). Although, the class of the current
sequence is fixed until the next transition, the pre-
dictions of K
bc
will make mistakes. In fact, just
like coin tosses, classification errors follow a Bi-
nomial distribution (with success probability p).
If the actual class of the current sequence is b, the
distribution of mistakes of K
bc
will follow a Bino-
mial distribution with p = TP
b
K
bc
, where TP
b
K
bc
is
the True Positive rate for class b and classifier K
bc
(i.e. the accuracy for class b obtained by classifier
K
bc
). On the other hand, if the actual class is c,
p = TP
c
K
bc
.
If the actual class is b, p can be estimated ( ˆp) from
a limited set of instances (we call it ’the window’),
and from standard statistical theory (and by as-
suming the Binomial distribution can be approxi-
mated by a Gaussian), it is known that ˆp belongs
to a confidence interval around p with confidence
α:
ˆp ∈ p + −z
α
r
p(1− p)
n
(3)
where n is the size of the window. From Eq 3, we
can estimate the size of the window required:
n ≥ z
2
α
p(1− p)
(p− 0.5)
2
(4)
When generating predictions, the actual class of
the current sequence is not known, and there-
fore we have to assume the worst case, that
happens when p is closest to 0.5. There-
fore, p = min(TP
b
K
bc
,TP
c
K
bc
). To be in the
safe side, for this paper, we have decided
to make the window size independent of the
classifier assigned to the current sequence.
Therefore, if there are three classes p =
min(TP
b
K
bc
,TP
c
K
bc
,TP
a
K
ab
,TP
b
K
ab
,TP
a
K
ac
,TP
c
K
ac
). A
similar analysis could be done for more than three
classes.
It is important to remark that Eq 4 is only a heuris-
tic approximation, since instances in a window are
not independent in the sense required by a Bi-
nomial distribution. For instance, if the user be-
comes tired and unfocused, s/he will generate a
sequence of noisy data that will be labeled uncor-
rectly. If the window includes that sequence of
mistakes, the classification based on that window
will also be mistaken. However, the classifier will
recover once the moving window goes past the se-
quence of mistakes.
BIOSIGNALS 2009 - International Conference on Bio-inspired Systems and Signal Processing
68

4 RESULTS
The aim of this Section is to show the results of our
method on the datasets described in Section 2. Let
us remember that there were three subjects, and each
one generated four sessions worth of data. The first
three sessions are available for learning while session
four is only for testing. All datasets are three-class
classification problems with classes named 2, 3, and
7.
Our method computes all two-class SMO classi-
fiers. SMO is the Weka implementation of a Sup-
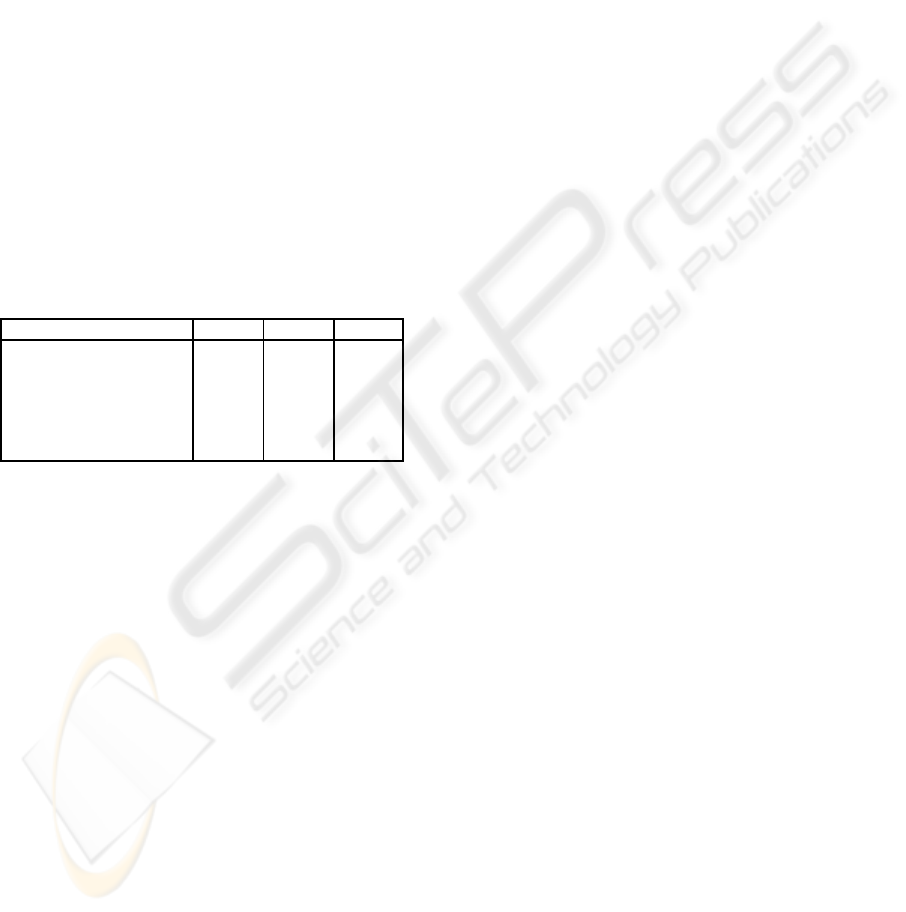
port Vector Machine. Table 1 displays the results of
all two-class classifiers (K
23
, K
27
, K
37
) and the three-
class classifier (K
237
). The training has been made
with sessions 1 and 2 instances and the testing with
session 3. The three-class classifier accuracies can
be used as a baseline to compare further results. In
brackets we can observe the True Positive rate (TP)
for each class. For instance, 74.7 is the True Positive
rate (TP) for class 2 for the K
23
two-class classifier
(i.e. TP
2
K
23
).
Table 1: Accuracy of two-class and three-class SMO clas-
sifiers for subjects 1, 2, and 3. Training with sessions 1 and
2, and testing with session 3.
SMO Subject 1 Subject 2 Subject 3
Classifier
K
23
79.0 71.9 52.3
(74.7/83.8) (68.2/75.3) (53.3/51.4)
K
27
82.4 74.3 57.9
(64.8/93.9) (62.7/81.9) (50.6/65.2)
K
37
83.0 76.8 60.4
(81.2/84.4) (63.5/87.7) (54.9/65.9)
K
237
73.8 62.0 40.9
Section 3 gives the details for computing the
thresholds for detecting transitions. These are: U
1
=
0.563108963, U
2
= 0.58576, U
3
= 0.587790606, for
subjects 1, 2, and 3, respectively.
Our method uses the TP rate (class accuracy), ob-
tained with session 3, for computing the moving win-
dow size, according to Eq 4. p will be set as the
minimum of all TP rates. So we have p
1
= 0.648,
p
2
= 0.627, and p
3
= 0.506 for subjects 1, 2, and
3, respectively. A confidence interval with α = 0.99
will be used, therefore z
α
= 2,5759. Table 2 displays
the windows sizes for every subject. It can be seen
that the window size for subject 3 requires 46072 in-
stances many more than available, so we apply the
window moving idea only to subjects 1 and 2. This
is due to the accuracy of classifiers for subject 3 are
very low, in particular the accuracy of K
23
(see Table
1). We have also computed the window size for larger
probabilities to check the performance of the method
if smaller window sizes are used. For instance, we
have also considered p
1
= 0.80 and p
2
= 0.70 (those
values are approximately the accuracies of the two-
class classifiers in Table 1).
Table 2: Window size used for subjects 1, 2, and 3.
Probability Window Size
Subject 1 0.648 78
Subject 2 0.627 92
Subject 3 0.506 46072
Subject 1 0.80 12
Subject 2 0.70 92
Finally, Table 3 shows the final results. The first
row displays the competition results (Galan et al.,
2005) on session four. (Galan et al., 2005) proposed
an algorithm based on canonical variates transforma-
tion and distance based discriminant analysis com-
bined with a mental tasks transitions detector. As re-
quired by the competition, the authors compute the
class from 1 second segments and therefore no win-
dows of samples are used. The second row, displays
the best results from the competition using longer
windows (Gan and Tsui, 2005) (it reduces dimension-
ality of data by means of PCA and the classification
algorithm is based on Linear Discrimination Analy-
sis). No details are given for the size of the win-
dow of samples. The third row shows the results of
the three-class classifier (sessions 1 and 2 were used
for training and session 4, for testing). The fourth
row contains the results (on session four) of apply-
ing the transition detector only. In this case, once the
transition is detected, the previous class is discarded
and the prediction is made using the two-class clas-
sifier chosen. These results are better than the three-
class classifier. For subject 3, the performance of the
method using the transition detection is very low be-
cause some of the two-class classifiers for subject 3
have a very low accuracy (see K
23
in Table 1). Let us
remember that when a transition is detected, the pre-
vious class is discarded. The previous class is com-
puted as the majority class of the previous sequence.
If the classifier used in the previous sequence is very
bad, the majority class might not be the actual class.
Hence, the wrong class would be discarded in the cur-
rent sequence, and the wrong 2-class classifier would
be selected. That would generate more mistakes that
would be propagated into the next sequence, and so
on. Given that all samples between transitions are
used to compute the previous class and that the (N-
1) classifiers are better than chance, the possibility of
mistaking the previous class is very low. In fact, for
the data used in this article, this situation has not oc-
curred. But it is important to remark that preventing
the propagation of the missclassification of the previ-
IMPROVING CLASSIFICATION FOR BRAIN COMPUTER INTERFACES USING TRANSITIONS AND A MOVING
WINDOW
69
ous class is crucial for the success of the method and
we intend to improve this aspect in the future.
The fifth row in Table 3 shows the results with
the method described in Section 3. In this case, both
ideas, the transition detection and the moving win-
dow size, are used. Results improve significantly if
the moving window is used: classification accuracy
raises from 74.8 to 94.8 and from 74.6 to 86.3 (sub-
jects 1 and 2, respectively). It can also be seen that
results are also improved if a smaller window size is
used (MW with small sample).
Comparing our method with the best competition
result that used a window of samples (second row of
Table 3), we can see that our method is competitive
with respect to the first subject and improves the per-
formance for the second subject. Unfortunately our
method cannot be applied to the third subject due to
the large number of samples required for the window.
It can also be seen that using windows improves accu-
racy significatively (second, fifth, and sixth rows ver-
sus the first one of Table 3).
Table 3: Results for subjects 1, 2, and 3.
Subj. 1 Subj. 2 Subj. 3
BCI comp. (1 sec.) 79.60 70.31 56.02
BCI comp. (long window) 95.98 79.49 67.43
3-class classifier 74.8 60.7 50.2
Transition detector 80.8 74.6 52.2
Moving window 94.8 86.3 -
MW small sample 84.2 82.5 -
5 SUMMARY AND
CONCLUSIONS
Typically, in BCI classification problems EEG sam-
ples are classified at every instant in time indepen-
dently of previous samples. These samples run in
sequences belonging to the same class, and then fol-
lowed by a transition into a different class. We present
a method that takes this fact into consideration with
the aim of improving the classification accuracy. The
general classification problem is divided into two sub-
problems: detecting class transitions and determin-
ing the class between transitions. Class transitions
are detected by computing the Euclidean distance be-
tween PSD at two consecutive times; if the distance
is larger than a certain threshold then a class tran-
sition is detected. Threshold values are automati-
cally determined by the method. Once transitions
can be detected, the second subproblem -determining
the class between transitions- is considered. First,
since the class before the transition is known, it can
be discarded after the transition and therefore, a N-
class problem becomes a (N-1)-class problem, which
is easier. Second, sequences between two transitions
may contain many instances but only a few are nec-
essary to determine the class of the whole sequence.
In order to determine the class between transitions a
moving window is used to predict the class of each
testing instance in such a way that only the n last pre-
dictions before the testing instance are taken into ac-
count. The estimation of the window size (n) is based
on standard statistical theory.
This method has been applied to a high quality
dataset which had been previously precomputed, re-
sulting in a three-class classification problem with 96
input attributes. These data corresponds to three sub-
jects, with four sessions for each one: three for train-
ing and one for testing. Several experiments have
been done in order to validate the method and the ob-
tained results show that just by applying the transition
detector, the classification rates are better than when
a 3-class classifier is used. When the moving window
is used, the results are significatively better. Those
results are also competitive to those obtained in the
BCI competition: similar for subject 1, better for sub-
ject 2, and worse for subject 3. We also show that if
a smaller window size is used the classification rates
are also better than those that use only the transition
detector and the three-class classifier.
REFERENCES
Curran, E. and Stokes, M. (2003). Learning to control brain
activity: a review of the production and control of eeg
components for driving braincomputer interface (bci)
systems. Brain Cognition, 51.
Dornhege, G., Krauledat, M., Muller, K.-R., and Blankertz,
B. (2007). Toward Brain-Computer Interfacing, chap-
ter General Signal Processing and MAchine Learning
Tools for BCI Analysis, pages 207–234. MIT Press.
G. Pfurtscheller, C. N. and Birbaumer, N. (2005). Mo-
tor Cortex in Voluntary Movements, chapter 14, pages
367–401. CRC Press.
Galan, F., Oliva, F., and Guardia, J. (2005). Bci competi-
tion iii. data set v: Algorithm description. In Brain
Computer Interfaces Competition III.
Gan, J. Q. and Tsui, L. C. (2005). Bci competition iii. data
set v: Algorithm description. In Brain Computer In-
terfaces Competition III.
Garner, S. (1995). Weka: The waikato environment for
knowledge analysis. In S.R. Garner. WEKA: The
waikato environment for knowledge analysis. In Proc.
of the New Zealand Computer Science Research Stu-
dents Conference, pages 57–64.
BIOSIGNALS 2009 - International Conference on Bio-inspired Systems and Signal Processing
70

Kubler, A. and Muller, K.-R. (2007). Toward Brain-
Computer Interfacing, chapter An Introduction to
Brain-Computer Interfacing, pages 1–26. MIT Press.
Mill´an, J. (2004). On the need for on-line learning in
brain-computer interfaces. In Proceedings of the In-
ternational Joint Conference on Neural Networks, Bu-
dapest, Hungary. IDIAP-RR 03-30.
Millan J del R, Renkens F, M. J. and Gerstner, W. (2004).
Noninvasive brain-actuated control of a mobile robot
by human eeg. IEEE Trans Biomed Eng, 51.
Vapnik, V. (1998). Statistical Learning Theory. John Wiley
and Sons.
IMPROVING CLASSIFICATION FOR BRAIN COMPUTER INTERFACES USING TRANSITIONS AND A MOVING
WINDOW
71
