
TOWARDS A FRAMEWORK FOR MANAGEMENT OF STRATEGIC
INTERACTION
Rustam Tagiew
Institute for Computer Science of TU Bergakademie Freiberg, Germany
Keywords:
Game theory, Multi-agent architecture, Human behavior, Domain-specific languages.
Abstract:
Our research aim is to construct a software framework and associated language for definition, providing and
recording of strategic interactions between real-world agents, human and artificial respectively. In this paper
we present an example of such interaction, which is used to show designed and partially implemented concepts.
We use FIPA based framework for our multi-agent system. The investigated scenario is a repeated two player
zero sum symmetric matrix game. We also conducted a study and analyzed the data.
1 INTRODUCTION
A strategic interaction (SI) are events, which happen,
if participants are interested in achieving something
and their success is depending on decisions of other
participants. The specialty of SI (called also game)
in real-world domain is the partial non-appearance
of game theoretical predictions (Tagiew, 2008). Es-
pecially in SI of humans, researchers use special
heuristics to model this deviation. This heuristics
are needed for programing advanced artificial agents,
who interact with humans. Our view is to construct
a prototype system, which helps to improve and stan-
dardize this heuristics from AI point of view. The sys-
tem is expected to provide and record human-human-
interaction through allocation of proxy agents for hu-
mans, which communicate over network. The behav-
ior of the system is based on the definition of the in-
teraction rules in special language and it also provides
an ability for definition of artificial agents. Artificial
agents can be tested against humans or each other. A
state-of-art multi-agent architecture is considered for
implementation. Assembling of concepts for build-
ing such a system on a concrete example is the aim
of this paper. Further we assume that the reader is fa-
miliar with game theory. After talking about games
and related works, we present a concept of using of a
multi-agent system (ch. 4) and a concept for defining
SI (ch. 5). Then, we present the study.
2 GAMES
Our concrete example is using of MSE by humans.
For humans, there are two problems to use mixed
strategy equilibrium (MSE) in repeated matrix games.
They are exact calculation of MSE and production
of an identical and independent distributed (iid) se-
quence (F.Camerer, 2003). Humans use a distribution
that is near to MSE and an equal distribution and they
avoid repetitions in the sequence. It is also interesting
to record human behavior in games with not only one
MSE. A set of games similar to Roshambo is chosen,
because they are fast to explain for test persons, fast to
play and have a simple structure for analyze of basic
concepts. These games are symmetric, zero sum, two
player,and the entries of the payoff matrix can be only
1(win), 0(draw) and −1(loss). The only difference to
simple Roshambo is that we use more than three ges-
tures. The payoff matrices of these games can be also
seen as adjacency matrices of directed graphs (set −1
to 0). There are 7 directed graphs for 3 gestures, 42
for 4, 582 for 5 and so on (Harary, 1957). We proved
all graphs for 5 gestures to find variants with only one
MSE non-equal distribution. There are 4 such vari-
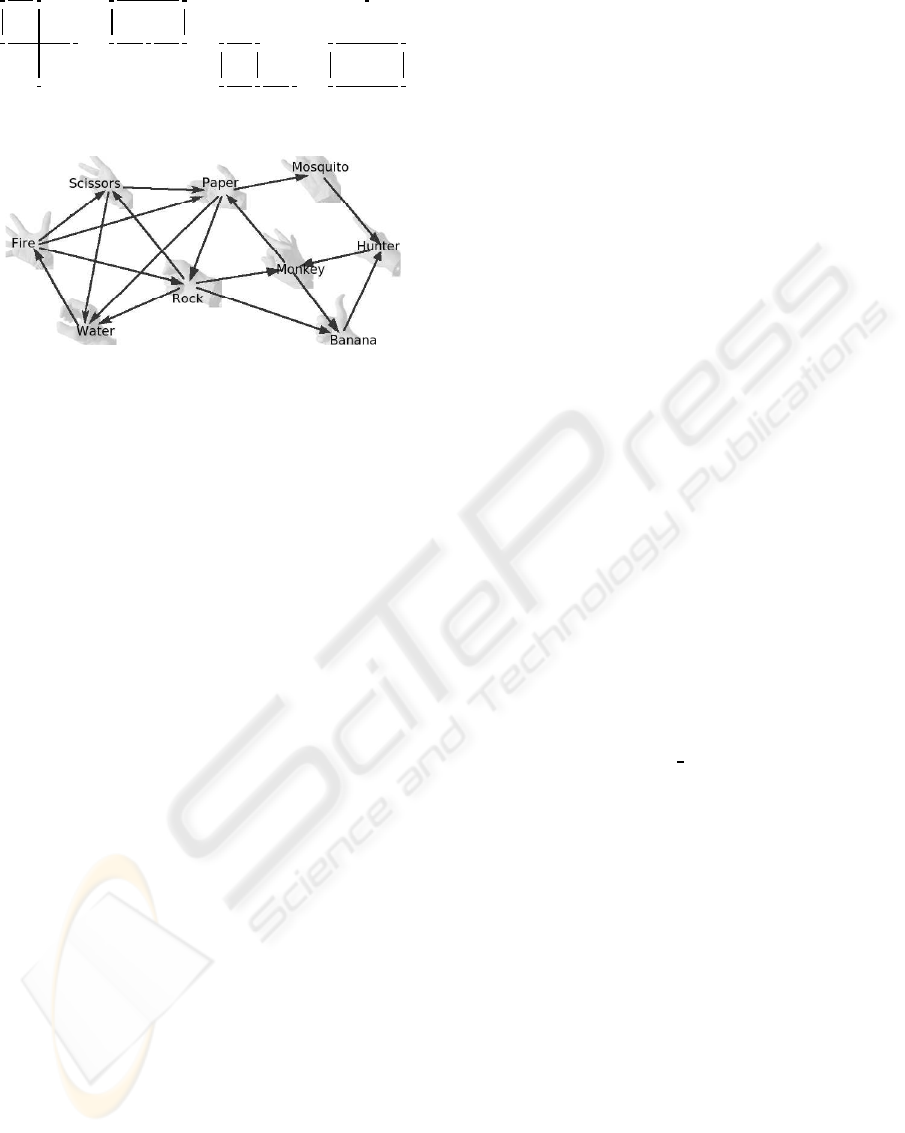
ants (Fig.1). The first variant is an existing American
variant of Roshambo with additional gestures fire and
water. We merged 3 of these graphs with probabili-
ties
1
9
and
1
7
and a 4-nodes cyclic graph to a graph of 9
nodes. Every node became a plausible name and hand
gesture. The resulting game framework is shown in
Fig.2. The cyclic 4-gesture variant Paper-Mosquito-
Hunter-Monkey has as MSE solution all distributions
on the line between points (0,
1
2
, 0,
1
2
) and (
1
2
, 0,
1
2
, 0).
587
Tagiew R. (2009).
TOWARDS A FRAMEWORK FOR MANAGEMENT OF STRATEGIC INTERACTION.
In Proceedings of the International Conference on Agents and Artificial Intelligence, pages 587-590
DOI: 10.5220/0001536505870590
Copyright
c
SciTePress
1
3
//
&&
L
L
L
L
L
L
L
L
L
L
L
L
L
L
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
1
9
1
7
1
7
oo
1
7
1
3
OO
1
9
]]:
:
:
:
:
:
:
:
oo
2
7
//
1
7
//
]]:
:
:
:
:
:
:
:
2
7
OO
1
6
1
6
oo
1
7
//
&&
L
L
L
L
L
L
L
L
L
L
L
L
L
L
1
7
]]:
:
:
:
:
:
:
:
1
9
AA
]]:
:
:
:
:
:
:
:
1
6
//
1
6
//
1
3
]]:
:
:
:
:
:
:
:
2
7
OO
88
r
r
r
r
r
r
r
r
r
r
r
r
r
r
2
7
oo
Figure 1: All nontrivial variants for 5 gestures.
Figure 2: Game framework.
3 RELATED WORKS
ACE is a general concept of software architecture for
investigation of economic processes(Tesfatsion and
Judd, 2006). ACE is a design for a multiagent sys-
tem consisting of four kinds of agents: worlds, mar-
kets, firms and consumers. Worlds and markets man-
age environmental data like ownership and current
prices. GDL is a logic-based language for definition
of a server for managing games between multiple pro-
grams(Genesereth et al., 2005). Finite games of per-
fect information are definable in GDL. Then, there is
a state-of-art games solving program GAMBIT.
4 FRAMASI
JADE (Bellifemine et al., 2001) is used for our frame-
work for management of SI (FRAMASI). Three types
of agents are defined: periphery agents, worlds and
participants (similar to ACE). A world represents the
SI itself. Participants search for worlds and then con-
tract with a world, about how and at which place
to participate. After closing contracts worlds supply
the associated participants with (partial) information
about the state of the interaction. Participants send
their actions to the world. Worlds die after fullfilled
interaction. A couple of periphery agents add some
extended abilities to our system like gesture recogni-
tion.
5 RUNNING PETRI NET
The idea for a definition language for practical rep-
resentation of SI in finite and discrete domains is us-
ing petri nets (PN). PN are usefull for representing
distributed processes (Priese and Wimmel, 2008). A
PN is a labelled directed graph, formally represented
through tuple:
PN = (P, Q, F, W, M) (1)
It consists of places P (circles), which can be filled
with a positive amount of tokens (dots), and transi-
tions Q (rectangles), which can be fired with an effect
on places. Places and transitions are disjunct P∩ Q =
⊘. Places can not be connected to places and transi-
tion not to transitions. Arcs F ⊆ (P×Q)∪(Q×P) are
weighted with positive natural numbers W : F → N
+
1
.
A transition can not be fired, when any place of in-
coming arcs have less tokens than its arc weight. Fir-
ing abolishes tokens of every incoming arc and pro-
duces tokens for every outgoing arc according to their
weights. The fill levels of the places represent the
state of the petri net. M ∈ N
|P|
is the current state
of PN. To model SI, PN is extended with tuple:
SI = (I, C, N, D, A, O, H, B) (2)
I is a set of agents, empty element ε stands for nature
or world accordingly. C ⊆ Q
∗
is a subset of sequences
of transitions, called choice sets. Every transition is
a member of only one element of C. N : C → N is a
numbering function and not injective. D : N → (R
1
0
)
n
is a function for firing probability distribution in
a choice set, where
∑
(D( )) = 1. n is number of
elements of the related choice sets. O : N → I ∪ ε
denotes ownership. A : Q → R
|I|
is the payoff vector
of a transition, if it fires. H : P → {I} provides for
every place a subset of agents for which it is hidden.
Agents can alter D for own numbers and see all
unhidden places. B : I → R is the current account
balance of agents.
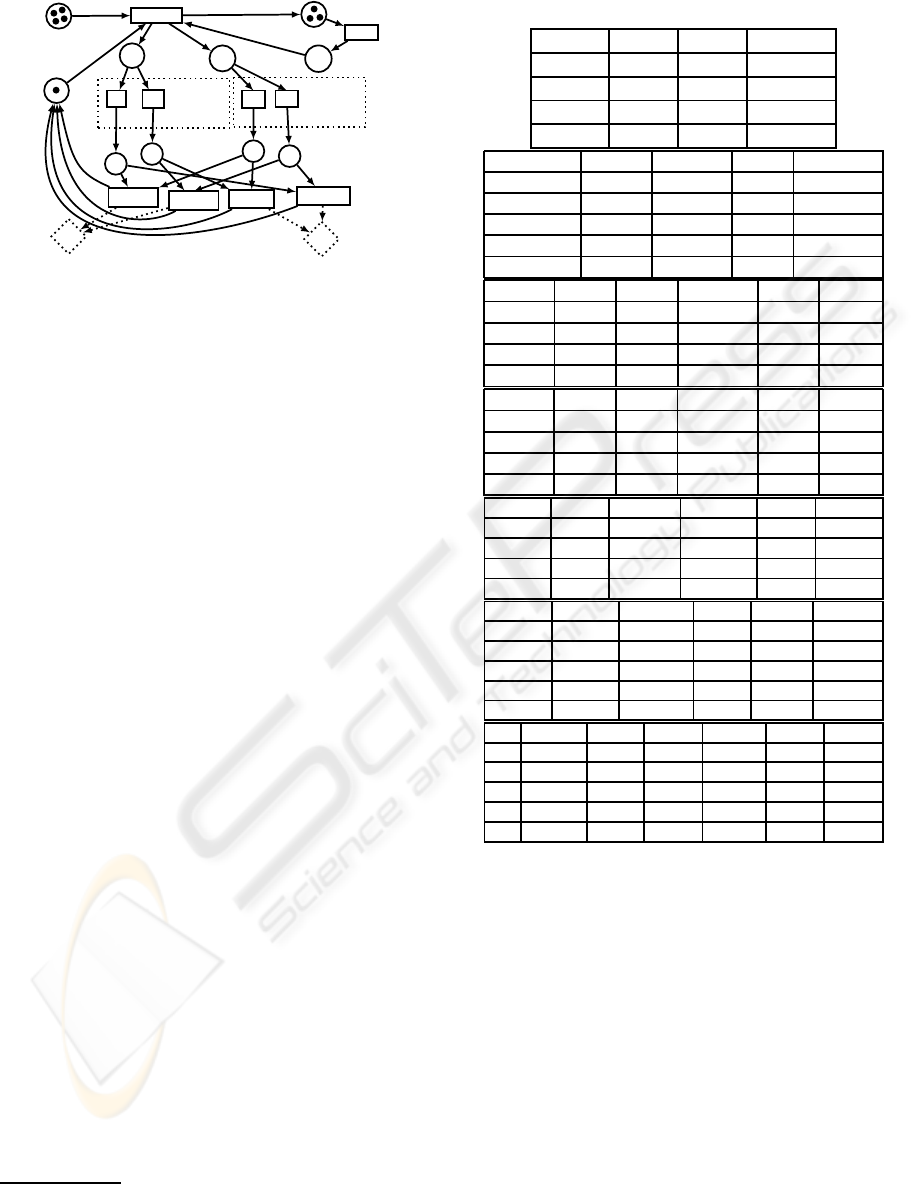
Fig.3 demonstrates a small application of this
formalism for a repeated game ”matching pennies”. It
is representative for our scenario. Dashed diamonds
are taken for the gathered payoff of players. Dashed
boxes are choice sets. Every transition, which is not
in dashed box, is in a single element choice set and
has a firing probability of 1. Altering of D must be
done at specific time, because it has a default state
and the transitions firing algorithm does not wait
for agents decisions. The places Ready and Time
shows to the participants, if they have or have not to
react. The weight ’latency’ between Time and Timer
represents the time period for simultaneous decisions.
ICAART 2009 - International Conference on Agents and Artificial Intelligence
588
A1
B1
A2
B2
Timer
Payoff4
Payoff1
Payoff2
Payoff3
Alice
Bob
Go1
Ready
m1
m2
m3
m4
20
10
Rounds
Go2
latency
tick
time
Alice
Bob
buffer
latency
Figure 3: Matrix Game using PNSI.
6 CONDUCTED STUDY
The feature of gesture recognition is added to our sce-
nario in sense of making it more situated and sim-
ilar to real-world physical activities like sport com-
petitions. We used a cyber-glove and a classifier for
recognition of gesture (Heumer et al., 2008). The
study was conducted on a thread of 200 one-shot
games of 7 kinds (41 to 61 tab.1) using our game
framework (fig.2). A player had a delay for consid-
eration of 6 sec for every shot. If he did not react,
the last or default gesture was chosen. A thread lasted
200 ∗ 6 sec = 20 min and had following structure -
30 times #31, 30x #41, 30x #51, 30x #52, 30x #53,
30x #54 and finally 20x #61. 10 test persons (com-
puter science undergrates in average 22, 7 years age
and 0.7 male) were recruited, had to play this thread
twice against another test person. In this way we gath-
ered 2000 one-shot games or 4000 single human de-
cisions. Every person got e 0.02 for a winned one-
shot game and e 0.01 for a draw. A winned thread
given additionally e 1 and a drawn e 0.5. Summa-
rized, a person could gain between e 0 and e 10 or in
average e 5. The persons, who played against each
other, sat in two separated rooms. One of the players
used the cyber-glove
1
and the another a mouse as in-
put for gestures. The proxy agent for a human player
has following features on his gui - own last and actual
choice, opponents last choice, graph of actual game,
timer and already gained money. According to state-
ments of the persons, they had no problems to under-
stand the game rules and to choose a gesture timely.
All winners and 80% of losers attested, that they had
fun to play the game.
1
except of one participant, who had to play both threads
with mouse, because of mismatch of cyber-glove size to her
hand
Table 1: MSE and observed distributions for all games.
31 Rock Paper Scissors
MSE .3333 .3333 .3333
All .36 .335 .305
Glove .3222 .3407 .3370
Mouse .3909 .3303 .2788
41 Hunter Monkey Paper Mosquito
MSE from 0 .5 0 .5
MSE to .5 0 .5 0
All .2783 .2533 .23 .2383
Glove .2704 .2407 .2444 .2444
Mouse .2848 .2636 .2182 .2333
51 Rock Paper Scissors Fire Water
MSE .1111 .1111 .1111 .3333 .3333
All .1867 .1533 .13 .3267 .2033
Glove .2222 .1555 .1259 .3 .1963
Mouse .1576 .1515 .1333 .3485 .2091
52 Rock Paper Monkey Fire Water
MSE .1429 .1429 .1429 .2857 .2857
All .1783 .155 .1767 .2983 .1917
Glove .1593 .1481 .2 .3 .1926
Mouse .1939 .1606 .1576 .297 .1909
53 Rock Banana Monkey Paper Hunter
MSE .1429 .1429 .1429 .2857 .2857
All .2133 .1417 .2433 .1883 .2133
Glove .1704 .1481 .2555 .2074 .2185
Mouse .2485 .1364 .2333 .1727 .2091
54 Hunter Monkey Paper Mosq. Banana
MSE f. 0 .5 0 .5 0
MSE t. .25 .25 .25 .25 0
All .1833 .3217 .1583 .1833 .1533
Glove .1704 .2963 .1481 .2148 .1704
Mouse .1939 .3424 .1667 .1576 .1394
61 Rock Paper Sciss. Monk. Fire Water
f 0.1111 .1111 .1111 0 .3333 .3333
t .1429 .1429 0 .1429 .2857 .2857
A .185 .0975 .0925 .12 .265 .24
G .2222 .0667 .0944 .1056 .2778 .2333
M .1545 .1227 .0909 .1318 .2545 .2455
7 RESULTS OF THE STUDY
Tab.1 presents the tables of theoretical and played dis-
tributions for every investigated game. For a game,
there are 10 ∗ 2 ∗ 30 = 600 and 10 ∗ 2∗ 20 = 400 for
61 recorded human decisions. In games 51 till 53,
at least one probability deviates with significance far
below 1h from MSE towards equal distribution. The
high probability of fire in 51 can be explained as best
response on equal distribution of the opponent. In
game 41, people prefer the middle one of extreme so-
lutions. But it can not be cleanly demonstrated on
games 54 and 61, because of consequences from the-
sis 1. Distribution during playing with glove deviates
from which with mouse. This thesis can be demon-
TOWARDS A FRAMEWORK FOR MANAGEMENT OF STRATEGIC INTERACTION
589

Table 2: Patterns probabilities for 31 and 41.
31 41 Bridges
Pattern The. Obs. The. Obs. 0 1 2
ABCD 0 0 .0938 .2611 0 0 0
ABCA .0741 .15 .0938 .1519 0 0 1
ABCB .0741 .1315 .0938 .0926 0 1 0
ABAC .0741 .1278 .0938 .0926 0 1 0
ABCC .0741 .0667 .0938 .087 1 0 0
ABBC .0741 .0796 .0938 .063 1 0 0
AABC .0741 .0685 .0938 .0722 1 0 0
ABBA .0741 .0611 .0469 .037 1 0 1
ABAB .0741 .0593 .0469 .0333 0 2 0
AABA .0741 .063 .0469 .0222 1 1 1
ABAA .0741 .0574 .0469 .0204 1 1 1
AABB .0741 .0463 .0469 .0222 2 0 0
ABBB .0741 .0352 .0469 .0204 2 1 0
AAAB .0741 .0352 .0469 .0185 2 1 0
AAAA .037 .0185 .0156 .0056 3 2 1
strated only in 5 of 7 games, where at least one of
probabilities for playing with glove significantly de-
viates from case, if it is played with mouse. But, there
is no plausible explanation for this deviation at time.
We counted tuples, which consists of own actual deci-
sion plus own three last decisions plus opponents last
three decisions. In game 31 for example, we have 4
tuples, each of them is observed 4 times. As exam-
ple, the tuple {rock, {rock, paper, scissors}, {paper,
rock, paper}} was observed in threads of four defer-
ent persons. The probability for one tuple in 31 to be
observed more than 3 times is about 0.126h. Persons
play in a rhythm which is far from iid. Further they
transform in consequence of this deviation a repeated
matrix game to an extensive game, in which one must
consider his turns in dependence of own and oppo-
nents last turns or in common speech fill the rhythm
of the game.
The latter brought us to calculate probabilistic
grammatic of human behavior in games 31 and 41.
We used methods of (Budescu and Rapoport, 1994).
Variables A, B, C, D, . . . ∈ gestures have all different
values. Patterns are abstract types of sequences and
constructed of these variables. For instance, the se-
quences {paper,rock} and {fire,water} are both of
pattern AB. We used patterns with length 4, because
of limited size of our data. We calculated theoreti-
cal probabilities of these patterns according to thesis,
that humans used equal distributions in games 31 and
41. Per game we can count (30 − 3) ∗ 2 ∗ 10 = 540
sequences and assign them to patterns. Additionally
we counted bridges (variable repetition) over 0, 1, 2
elements in the patterns for possible explanation of
deviation. Tab.2 shows the results.
8 CONCLUSIONS
Our paper showed a practical way for construction
of a highly scaleable multi-agent system for defini-
tion, providing and recording of SI between real-
world agents, human and artificial respectively. Espe-
cially, we presented a multi-agent system design and
a PN based language. It produced data for a concrete
scenario - using MSE in zero sum by humans. The
recorded data was analyzed and showed results simi-
lar to already alluded in literature. Core elements of
our system can be downloaded from our home page.
REFERENCES
Bellifemine, F., Poggi, A., and Rimassa, G. (2001). Jade: a
fipa2000 compliant agent development environment.
In AGENTS ’01. ACM.
Budescu, D. V. and Rapoport, A. (1994). Subjective ran-
domization in one- and two-person games. Journal of
Behavioral Decision Making, 7.
F.Camerer, C. (2003). Behavioral Game Theory. Princeton
University Press, New Jersey.
Genesereth, M. R., Love, N., and Pell, B. (2005). General
game playing: Overview of the aaai competition. AI
Magazine, 26(2):62–72.
Harary, F. (1957). The number of oriented graphs. Michigan
Math. J., 4.
Heumer, G., Amor, H. B., and Jung, B. (2008). Grasp recog-
nition for uncalibrated data gloves: A machine learn-
ing approach. Presence: Teleoper. Virtual Environ.,
17:121–142.
Priese, L. and Wimmel, H. (2008). Petri-Netze. Springer.
Tagiew, R. (2008). Simplest scenario for mutual nested
modeling in human-machine-interaction. In Advances
in Artificial Intelligence. Heidelberg, Springer.
Tesfatsion, L. and Judd, K. (2006). Handbook of computa-
tional economics, volume 2. Elsevier/North-Holland.
ICAART 2009 - International Conference on Agents and Artificial Intelligence
590
