NEW FAST TRAINING ALGORITHM SUITABLE FOR

HARDWARE KOHONEN NEURAL NETWORKS DESIGNED

FOR ANALYSIS OF BIOMEDICAL SIGNALS

Rafał Długosz

Swiss Federal Institute of Technology in Lausanne, Institute of Microtechnology

Rue A.-L. Breguet 2, CH-2000, Neuchâtel, Switzerland

Marta Kolasa

University of Technology and Life Sciences, Institute of Electrical Engineering, ul. Kaliskiego 7, 85-791, Bydgoszcz, Poland

Keywords: Kohonen Neural Network, Optimized learning process, Linear and nonlinear filtering, WBSN applications.

Abstract: A new optimized algorithm for the learning process suitable for hardware implemented Winner Takes Most

Kohonen Neural Network (KNN) has been proposed in the paper. In networks of this type a neighborhood

mechanism is used to improve the convergence properties of the network by decreasing the quantization

error. The proposed technique bases on the observation that the quantization error does not decrease

monotonically during the learning process but there are some ‘activity’ phases, in which this error decreases

very fast and then the ‘stagnation’ phases, in which the error does not decrease. The stagnation phases

usually are much longer than the activity phases, which in practice means that the network makes a progress

in training only in short periods of the learning process. The proposed technique using a set of linear and

nonlinear filters detects the activity phases and controls the neighborhood R in such a way to shorten the

stagnation phases. As a result, the learning process may be 16 times faster than in the classic approach, in

which the radius R decreases linearly. The intended application of the proposed solution will be in Wireless

Body Sensor Networks (WBSN) in classification and analysis of the EMG and the ECG biomedical signals.

1 INTRODUCTION

Application of Artificial Neural Networks (ANNs)

in medical diagnostic tools may be observed for

many years, e.g. in classification of biomedical

ECG, EMG signals (Osowski, 2001), (Ghongade,

Ghatolfor, 2007), segmentation and analysis of brain

or mammography images (Wismüller et al., 2002)

and many others.

In most cases ANNs are realized using software

platforms that is very convenient, but such networks

cannot be used in low power diagnostic devices.

Authors recently designed an experimental

Kohonen network in CMOS technology that enables

parallel data processing (Długosz et al. 2008),

(Długosz and Kolasa 2008). Networks of this type

may be hundreds times faster than networks realized

in software, consuming much less energy.

Various optimization techniques of the learning

algorithm for KNN have been proposed (Zeb Shah,

Salim, 2006), (McInerney, Dhawan 1994) but these

techniques are not suitable for hardware networks

due to large computational complexity. In this paper

a new optimized learning algorithm is proposed that

bases on simple filters, which makes this technique

much easier to implement in hardware. This

technique will be used in a next prototype of the

KNN in analysis of biomedical ECG and EMG

signals in Wireless Body Sensor Networks (WBSN).

Extracting the useful features of the ECG and the

EMG signals for use with ANNs is the problem

itself, which has been addressed by many papers e.g.

(Ghongade, Ghatolfor, 2007). In this paper example

simulation results are presented for selected training

data that are representative for different applications,

but can easily be adopted to biomedical data.

364

Długosz R. and Kolasa M. (2009).

NEW FAST TRAINING ALGORITHM SUITABLE FOR HARDWARE KOHONEN NEURAL NETWORKS DESIGNED FOR ANALYSIS OF BIOMEDICAL

SIGNALS.

In Proceedings of the International Conference on Biomedical Electronics and Devices, pages 364-367

DOI: 10.5220/0001536703640367

 SciTePress

2 KOHONEN NEURAL

NETWORK

Kohonen neural networks typically consist of a

single layer of neurons arranged as a map, with the

number of outputs equal to the number of neurons,

and the number of inputs equal to the number of

weights in neurons. In practical applications 2-D

maps are the most commonly used

, since they allow

for good data visualization (Kohonen 2001).

Training data files in such networks consist of m

n-elements patterns X, where n is the number of the

network inputs. The competitive learning in KNN is

an iterative process. During each iteration, called an

epoch, all m vectors are presented to the network in

a random order. The full learning process requires

even hundreds epochs, which means even several

hundreds thousands presentations of a single pattern.

Once a single pattern is presented to the network,

several calculation steps may be performed by the

network. In the first step a distance between a given

pattern X and the weights vector W in every neuron

in the map is calculated using, for example, the

Euclidean or the Manhattan metric. In the next step

the winning neuron is identified, and this neuron in

the following step is allowed to adapt its weights.

In the Winner Takes All (WTA) learning method

only the winning neuron, whose vector W is the

closest to the pattern X, is allowed to adapt the

weights, while in the Winner Takes Most (WTM)

approach also neurons that belong to the winner’s

neighborhood change the weights.

The WTA algorithm offers poor convergence

properties, especially in case of large number of

neurons. In this approach some neurons remain dead

i.e. they absorb the computational resources, but

never win and never become representatives of any

data class. The WTM algorithm, on the other hand,

is more complex, since it additionally involves the

neighborhood mechanism, which increases the

computational complexity, but this mechanism

usually activates all neurons in the network (Mokriš

2004), thus minimizing the quantization error. This

error is defined as follows (w

are weights of the

winning neuron):

Qerr

∑∑

−

)(

(1)

The main problem in the WTM algorithm is very

large number of operations, especially in case of

large number of patterns and epochs. In hardware

implementations effective methods to minimize the

number of operations are therefore required.

3 THE PROPOSED TECHNIQUE

In a typical WTM learning algorithm the neighbor-

hood radius R at the beginning of the training

process is set up to the maximum possible value so it

covers an entire map. After each epoch the radius R

decreases linearly by a small value to zero. In

practice, as number of epochs usually is much larger

than the maximum value (R

max

) of the neighborhood

radius R, therefore the radius decreases always by

‘1’ after the number of epochs equals to:

(

)

MAX

round Rll

(2)

In equation (2) l

max

is the total number of epochs in

the learning phase. Value of the l parameter usually

is in the range between 20 and 200

, depending on the

network’s dimensions. In case of an example map

with 10x10 neurons and the rectangular neighbor-

hood R

max

equals to 19 (Długosz and Kolasa, 2008).

To verify this ‘linear’ approach authors designed

a software model of the WTM KNN. Simulations

have been performed for different network dimen-

sions and different training data files. Observation of

the quantization error in the time domain shows that

the ‘linear’ approach is not optimal. The example

illustrative waveforms of the Q_error are in this case

shown in Fig. 1 for an example training data file

with 1000 patterns X, for selected network dimen-

sions 20x20, 10x10 and 4x4 neurons. The quantiza-

tion error is calculated after each epoch i.e. always

after presentation of 1000 training patterns X. This

does not increase significantly the computational

complexity of an entire learning process.

The first important observation is that when the

neighborhood radius R is larger than some critical

value, the quantization error does not decrease,

which means that in this period the network does not

make the progress in training. This critical value is

usually small, between 4 and 7 for different network

dimensions as illustrated in Fig. 1. The important

conclusion at this point is that the learning process

may start with the value of the radius R, which is

much smaller than the maximal value R

max

. This

significantly shorts the entire training process.

The second important observation is that the

error does not decrease monotonously with time, but

there are some distinct activity phases, just after the

radius R is switched to the smaller value, in which it

decreases abruptly and then some stagnation phases,

in which it does not decrease. The length of a single

activity phase usually is between 2-4 epochs inde-

pendently on the network dimensions.

The optimization technique proposed by authors

eliminates these stagnation phases by incorporation

of the multistage filtering of the quantization error in

NEW FAST TRAINING ALGORITHM SUITABLE FOR HARDWARE KOHONEN NEURAL NETWORKS

DESIGNED FOR ANALYSIS OF BIOMEDICAL SIGNALS

365

time domain and a special decision mechanism that

automatically switches over the radius R just after a

given activity phase is finished. This starts a new

activity phase, but for smaller value of the radius R.

Quantization error [10E-3] (20x20 neurons)

0.02

0.04

0.06

0.08

0.1

0.12

0.14

0.16

0.18

0 200 400 600 800 1000 1200

Epoch No.

No progress in training

R = 8

R = 0

Quantization error [10E-3] (10x10 neurons)

0.02

0.04

0.06

0.08

0.1

0.12

0.14

0.16

0 200 400 600 800 1000 1200

Epoch No.

No progress

= 6

= 0

Quantization error [10E-3](4x4 neurons)

0.02

0.04

0.06

0.08

0.1

0.12

0.14

0 200 400 600 800 1000 1200

Epoch No.

R = 3

R = 0

Activity phase

Stagnation phase

Figure 1: Typical ‘linear’ training process: (top) an e.g.

training data file with 1000 vectors X and final placement

of neurons in the map (below) quantization error as a

function of the Epoch No., for selected map’s dimensions.

In our proposed method three filters have been

applied. The entire cycle starts with a lowpass finite

impulse response (FIR) filtering that smoothes out

the initial error waveform. This process is illustrated

in Fig. 2 (a). In this case a simple Butterworth flat

filter has been used with the following coefficients:

LPi

= {0.125, 0.375, 0.375, 0.125}.

Original Q_ERROR [10E-3] and after LOWPASS FILTERING

0.01

0.03

0.05

0.07

0.09

0.11

0.13

0.15

0 200 400 600 800 1000 1200

Epoch No.

error 'noise'

(a)

HIGHPASS FILTERING

-0.01

0.01

0.02

0.03

0 200 400 600 800 1000 1200

Epoch No.

Activity phase

Stagnation phase

"noise" spike

(b)

MEDIAN NONLINEAR FILTERING

-0.006

-0.004

-0.002

0.002

0.004

0.006

0.008

0.01

0.012

0 200 400 600 800 1000 1200

Epoch No.

threshold level

Activity phase

"noise" spike

(c)

Figure 2: Proposed 3-stage error filtering: (a) the original

waveform and the lowpass, (b) the highpass, (c) the

nonlinear median filtering.

The next step is the highpass filtering operation

that detects edges in the smoothed error waveform.

This filter may be very simple, with the length not

exceeding 4. In presented example a filter with the

coefficients h

HPi

= {1, 1, -1, -1} has been employed.

The resultant waveform is illustrated in Fig. 2 (b).

The spikes in this waveform indicate the activity

phases. The problem here is that the “noise” present

in the initial error waveform is a source of additional

undesired spikes, which often are as high as the

‘activity’ spikes, although usually are narrower than

the ‘activity’ spikes. To overcome this problem a

nonlinear median filter has been additionally

applied. The length of this filter has been selected in

such a way to even the height of the ‘activity’ spikes

and to eliminate the ‘noise’ spikes. For example, the

length of 5 allows to eliminate the ‘noise’ spikes

with the width equal to 2, as shown in Fig. 2 (c).

Both the highpass and the median waveforms are

then used by a decision mechanism that automati-

cally switches over the radius R to the smaller value.

The decision procedure starts when the value of the

‘median’ waveform becomes larger than some

BIODEVICES 2009 - International Conference on Biomedical Electronics and Devices

366

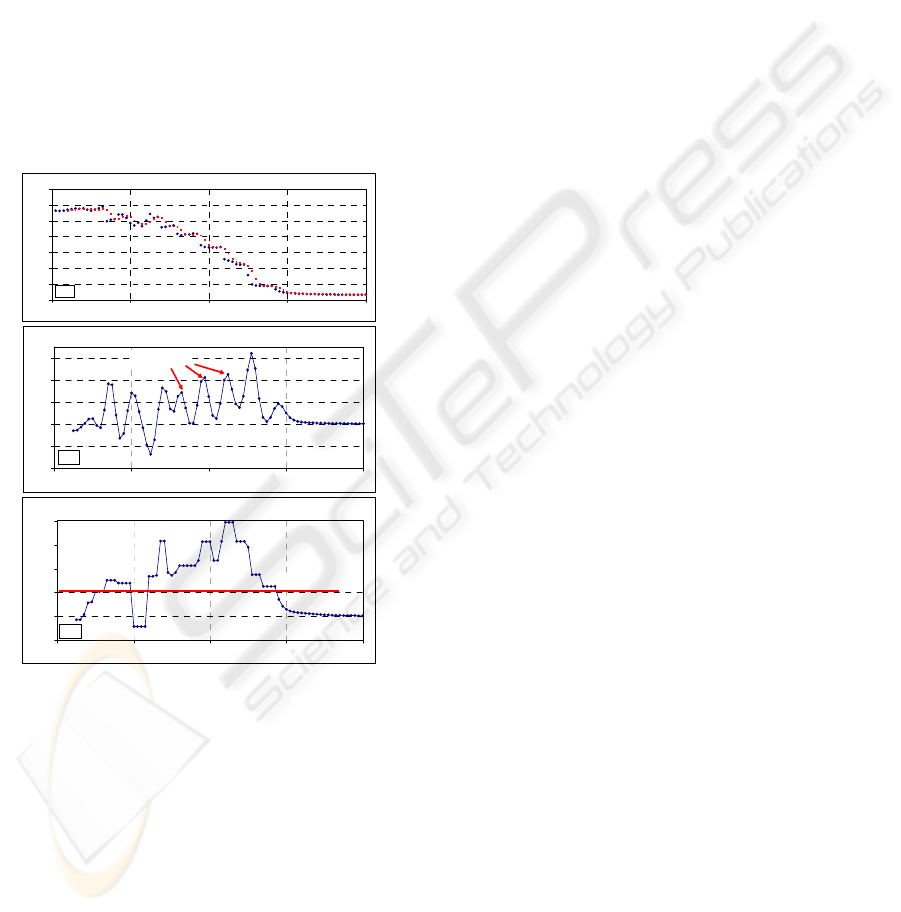
threshold value, which is high enough to exclude the

‘noise’ spikes. The decision about switching over is

made when the signal in the ‘highpass’ waveform

becomes falling, which means that the training

process is just entering the stagnation phase.

It is worth noticing that the proposed algorithm

must cooperate with the classic ‘linear’ method. This

is necessary in a situation, in which an activity spike

in the median waveform would be to small to

activate the decision procedure. In this case the

‘linear’ method will switch over the radius R after l

iterations that will stop a given stagnation phase.

The illustrative simulation results in case of the

optimized training process are shown in Fig. 3 for an

example network with 10x10 neurons. In this case

the entire training process has been shorten 16 times

from initial 1000 epochs to 60 epochs.

Original Q_ERROR [10E-3] and after LOWPASS FILTERING

0.01

0.03

0.05

0.07

0.09

0.11

0.13

0.15

020406080

Epoch No.

(a)

HIGHPASS FILTERING

-0.02

-0.01

0.01

0.02

0.03

0 20406080

Epoch No.

ctivity phase

(b)

MEDIAN NONLINEAR FILTERING

-0.004

0.004

0.008

0.012

0.016

020406080

Epoch No.

threshold level

(c)

Figure 3: Training process after optimization, for an e.g.

map with 10x10 neurons: (a) original signal and after the

lowpass, (b) the highpass and (c) the median filtering.

4 CONCLUSIONS

A new simple learning algorithm for WTM KNNs

designed for low-power devices has been described

in the paper. The proposed technique bases on the

multistage filtering of the quantization error, which

is calculated after each epoch of the training process.

The proposed algorithm detects the periods in the

training process, in which the error decreases i.e. in

which the network makes a progress in training and

then automatically switches over the neighborhood

radius R just after the training process enters the

stagnation phase, thus shortening this phase.

The simulations show that this technique is able

to shorten the training process by more than 90%.

The proposed algorithm will be used in hardware

KNNs, designed for analysis of biomedical the ECG

and the EMG signals in Wireless Body Sensor

Network (WBSN) applications.

ACKNOWLEDGEMENTS

The work is supported by EU Marie Curie Outgoing

International Fellowship No.

021926

REFERENCES

Osowski, S., Tran Hoai Linh, “ECG beat recognition using

fuzzy hybrid neural network”, IEEE Transactions on

Biomedical Engineering, Vol.48, Issue 11, Nov. 2001

Wismüller A., Lange O., Dersh R. D., Leinsinger

G. L., Hahn K., Pütz B., and Auer D. “Cluster Analy-

sis of Biomedical Image Time-Series”, International

Journal of Computer Vision, Vol. 46, No. 2, Feb. 2002

Jehan Zeb Shah, Naomie bt Salim, “A Fuzzy Kohonen

SOM Implementation and Clustering of Bio-active

Compound Structures for Drug Discovery”, IEEE

Symposium on Computational Intelligence and

Bioinformatics and Computational Biology (CIBCB),

28-29 September 2006

M. McInerney, A. Dhawan, Training the self-organizing

feature map using hybrids of geneticand Kohonen

methods Neural Networks, IEEE World Congress on

Computational Intelligence, Vol.2, 27 Jun-2 Jul 1994

Rajesh Ghongade, A. A. Ghatol, “Performance Analysis

of Feature Extraction Schemes for Artificial Neural

Network Based ECG Classification”, International

Conference on Computational Intelligence and

Multimedia Applications (ICCIMA), 2007, Vol. 2

T. Kohonen, Self-Organizing Maps, third edition, Springer

Berlin, 2001

Mokriš, R. Forgáč, “Decreasing the Feature Space

Dimension by Kohonen Self-Orgaizing Maps”, 2

Slovakian – Hungarian Joint Symposium on Applied

Machine Intelligence, Herľany, Slovakia 2004

Długosz R., Talaśka T., Dalecki J., Wojtyna R.,

“Experimental Kohonen Neural Network Implemented

in CMOS 0.18μm Technology”, 15th International

Conference Mixed Design of Integrated Circuits and

Systems (MIXDES), Poznań, Poland, June 2008

Długosz R., Kolasa M., “CMOS, Programmable,

Asynchronous Neighborhood Mechanism For WTM

Kohonen Neural Network”, 15th International

Conference Mixed Design of Integrated Circuits and

Systems (MIXDES), Poznań, Poland, June 2008

NEW FAST TRAINING ALGORITHM SUITABLE FOR HARDWARE KOHONEN NEURAL NETWORKS

DESIGNED FOR ANALYSIS OF BIOMEDICAL SIGNALS

367