
COMPUTATIONAL MUSCLE REFLEX MODEL OF WHEELCHAIR
USERS TRAVELING IN MOTOR VEHICLES
Evaluation of the Motion and the Myoelectric Potential of People with Disabilities
Junichi Takano, Shigeru Aomura
System design, Tokyo Metropolitan University, Hino, Tokyo, Japan
Emiko Kikuchi
Health Science, Tokyo Metropolitan University, Tokyo, Japan
Keywords:
Muscle reflection model, Wheelchair, Seatbelt, People with disabilities.
Abstract:
In this study, a human motion computer model in a wheelchair was developed to evaluate the effectiveness of
a seatbelt for people with disabilities traveling in a motor vehicle. The human model was composed of two
rigid links and three masses. This model was characterized with muscle reflection defined by Hill’s equation.
A sudden stop experiment by using a carriage on which a wheelchair was fixed with a subject was performed
to obtain the human muscle parameters and to evaluate the model. Volunteer subjects including people with
disabilities participated in the experiment. The motion and muscle activity of a subject wearing a seatbelt were
simulated by this model. The muscle reflection of people with disabilities was stronger than that of normal
people in the case of not using a seatbelt, but in the case of using a seatbelt the muscle reflection of people with
disabilities was similarly weak with normal people. The result of computer simulation showed that a seatbelt
is more important for people with disabilities than for normal people.
1 INTRODUCTION
Wheelchair users traveling in motor vehicles have
been increasing dramatically. There is a need to im-
prove the safety standards for transporting wheelchair
users (ANSI/RESNA, 2002) (W.E.Fisher, 1987). The
authors carried out a questionnaire for wheelchair
users who frequently traveled in motor vehicles. The
results showed that even though they used seatbelts,
they still felt a strong insecurity during sudden car
stops (Aomura, 2007). The motion of people with
disabilities at a sudden stop should be examined more
in detail.
Computer models are quite effective and widely used
in order to simulate the human motions (Bertocci,
2001) (Bertocci, 2000), by many researchers. In re-
cent years, human motion models have been used
in simulations for crash experiments. For example,
Bertocci (Bertocci, 1999) has used a dynamic lumped
mass crash simulator to develop a model of a re-
strained occupant subjected to a 20g/30mph frontal
motor vehicle crash. And Moorcroft (Mooreroft,
1999) demonstrated that motor vehicle crashes could
be simulated with the use of MADYMO, a program
designed specifically for occupant safety analysis.
However, the model that can simulate the motion of
people with disabilities has not been developed. The
goal of this study is to make a computer model which
can simulate the motion of people with disabilities
supported by a seatbelt.
In this study, a rigid link model of a human body sit-
ting in a wheelchair was designed with muscle reflec-
tion characteristics to demonstrate the motion of peo-
ple with disabilities. Although normal people gen-
erally show a similar muscle reflection pattern, the
muscle reflection pattern of people with disabilities
depends on the extent of each disorder. Therefore, the
experiment was carried out on two hemiplegia sub-
jects and a quadpledia subject.
As a result, the motion of subject with disabilities
could be simulated by using muscle parameters and
this computer model was a useful tool to evaluate the
motion of wheelchair users with a seatbelt.
80
Takano J., Aomura S. and Kikuchi E. (2009).
COMPUTATIONAL MUSCLE REFLEX MODEL OF WHEELCHAIR USERS TRAVELING IN MOTOR VEHICLES - Evaluation of the Motion and the
Myoelectric Potential of People with Disabilities.
In Proceedings of the International Conference on Bio-inspired Systems and Signal Processing, pages 80-86
DOI: 10.5220/0001537900800086
Copyright
c
SciTePress
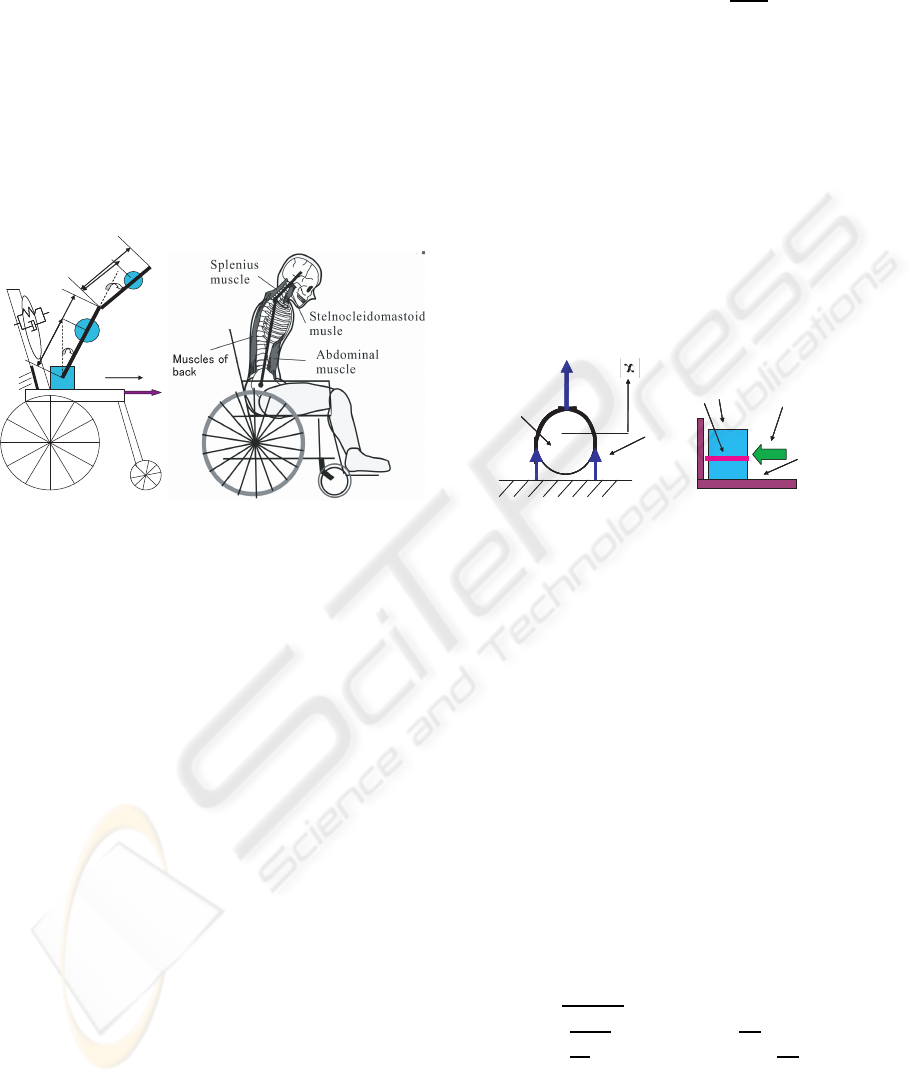
2 PHYSICAL MODEL
2.1 Rigid Link Model
A two dimensional rigid link model sitting in a
wheelchair is shown in Fig.1. This model is a three
degrees of freedom and composed of a head, a trunk
and a hip. A center of gravity for the head and trunk
is located in the center of each rigid body. A dy-
namic equation for the rigid link model is given in
equation(1).
L2
r2
k1 L1
c1 L2
m0
m2
m1
㱔1
㱔2
Figure 1: Schematic image of a human rigid link model
fixed by a seatbelt in the wheelchair.
D
q(t)
¨q(t) +C
q(t), ˙q(t)
+S
q(t), A
x0
(t)
= M
q(t), ˙q(t), a(t)
(1)
Input is the surface acceleration A
x0
and outputs
are the horizontal displacement of lumbar spine x and
the angle of cervical and trunk θ
1
, θ
2
, C is the term
of the mass of each part and velocity of angle, D is
the term of the moment of inertia of each link, S is the
term of the tension of shoulder and waist of a seatbelt,
M is the torque of each joint generated by a muscle ac-
tivity. M is composed of an active and passive muscle
activity. a is the myoelectric potential.
2.2 The Model of a Seatbelt and the
Friction Force of a Seating Surface
For this study, the seatbelt made by synthetic fibers
of polyamide was used. The seatbelt is called energy
absorbing webbing. The overhead view of the cross
section of a human body with a seatbelt is shown in
Fig.2. A human body was fixed by the seatbelt with
tension S. The tension of the seatbelt S works on the
shoulder and the waist. The tension of the seatbelt is
given by Nakajima’s equation as follows.
S
i
= 2S
m
(1− exp(
−2x
ε
0
L
0
)) (2)
where L
0
is the length of a seatbelt, S
m
is the maxi-
mum tension of a seatbelt and ε
0
is the strain amount
of a seatbelt.
The hip sinks down and moves forward when a
motor vehicle stops causing friction force between hip
and seating surface. The motion in the horizontal di-
rection is affected by friction force. Fig.2 shows the
frictional force between seating surface and hips. It is
difficult to measure friction force by the experiment.
In this study, the friction force was calculated by using
the Kaminishi’s (Uenishi, 2005) equation(3) of static
analysis.
F f
0
= 0.4S
0
(3)
Seatbelt
Human body
fF 2=
f
f
Seatbelt
Human body
fF 2=
f
f
Reaction forceBelt
Body
µ
;Frictional force
Reaction forceBelt
Body
µ
;Frictional force
Figure 2: The overhead view of cross section diagram of a
human body with a seatbelt and frictional force of seating
surface.
2.3 The Muscle Activity Model
There are many reports about muscle activity. For
example, Hase carried out a computer simulation of
the human movement by using a musculo-skeletal
model (Hase, 2002). In this study, the muscle reflec-
tion results were obtained by using the Hill’s equation
to express the motion of people with disabilities. A
force of muscle contraction f is described by Hill’s
Eq.(4).
f = aF(l,V) (4)
Where l is the length of muscle, V is the contrac-
tion rate and a is the myoelectric potential. When the
length of muscle and the contractile rate is known, the
muscle tension force F
max
can be calculated.
F
max
=
(B−0.3V)
B+V
F
a
(l) if (V > 0)
(
−1.3V
B
+ 1)F
a
(l) if (
−B
3
< V < 0)
(
1.3
3
+ 1)F
a
(l) if (V <
−B
3
)
(5)
F
a
(l) =
¯
F[1− K
1
(l
r
− l)] if (l < l
r
)
¯
F[1− K
2
(l − l
r
)] if (l > l
r
)
(6)
Where l
r
is the initial length of each muscle,
¯
F is the
maximum muscle force of isometric contraction, B is
COMPUTATIONAL MUSCLE REFLEX MODEL OF WHEELCHAIR USERS TRAVELING IN MOTOR VEHICLES -
Evaluation of the Motion and the Myoelectric Potential of People with Disabilities
81

Figure 3: A muscle model of a sternocleidomastoid and a
splenius.
the parameter of each muscle, K
1
and K
2
are the con-
stant. The sternocleidomastoid muscle, the splenius
muscle, the abdominal muscle and the back muscles
are used to return the body to its original position.
The length of extensor and flexor muscles are shown
in Fig.3.
2.4 The Model of Myoelectric Potential
The myoelectric potential is the electrical manifesta-
tion of the neuromuscular movement associated with
a contracting muscle. It is an exceedingly compli-
cated signal which is affected by the anatomical and
physiological properties of muscles (Luca, 1979).
In this study, it was assumed that the myoelectric po-
tential would be greater when the angular displace-
ment θ, the angular velocity
˙
θ of subjects and the ac-
celeration A
x0
of the carriage device were stronger.
The myoelectric potential is given by following equa-
tion.
a = 1− exp
−
kθ(t − τ) + b
˙
θ(t − τ)+
cA
x0
(t − τ) + a
0
}] (7)
where k, b and c are the human muscle parameters,
τ is the time lag and a
0
is the steady state myoelectric
potential.
2.5 The Passive Torque
In this study, a passive torque on ligament and soft
tissue was described by Yamazaki’s passive muscle
model (Ogihara, 2000) and given in Eq.(8).
T
p
= p
1
exp p
2
(θ− p
3
) − p
4
exp p
5
(p
6
− θ) + q
˙
θ (8)
where q is the viscosity resistance, p
3
,p
6
are the co-
efficients that detemines angle when elasticity resis-
tance increases. p
1
,p
4
are the coefficients that deter-
mines elastic constant when ligament and soft tissue
become stiff. p
2
,p
5
are the coefficients which de-
scribes nonlinearity of an elastic resistance.
3 CRASH EXPERIMENT
3.1 The Method of Experiment
In this study, two experiments were performed. The
purpose of the first experiment was to determine the
muscle parameters of a subject. The purpose of the
second experiment was to evaluate the motion of the
subjects and the model.
A carriage experiment device was used instead of a
motor vehicle. The carriage experiment device is
shown in Fig.4. The forward crash can simulate a sud-
den stop. A wheelchair (JIS T 9201) was attached to
a metal structure which was harnessed to the carriage
device.
Figure 4: A wheelchair fixed on a carriage experiment de-
vice instead of a motor vehicle.
The acceleration of the carriage device was
measured to compare with that of a car. Fig.5 shows
the comparison of seating face acceleration between
the carriage device and a car. The carriage device
can be used instead of a motor vehicle because the
maximum acceleration and convergence time of the
carriage device matched that of a car.
A normal subject (aged 24), right and left hemi-
plegia subjects by bleeding in the brain (aged 55, 59)
and a quadriplegia subject by a cerebral palsy (aged
29) participated in the experiment. All subjects were
male. The disabled subjects were selected from many
volunteers through the cooperation of a welfare orga-
nization. All subjects signed informed consent forms.
BIOSIGNALS 2009 - International Conference on Bio-inspired Systems and Signal Processing
82
㪄㪏
㪄㪍
㪄㪋
㪄㪉
㪇
㪉
㪇 㪌㪇㪇 㪈㪇㪇㪇 㪈㪌㪇㪇 㪉㪇㪇㪇
㪫㫀㫄㪼㩿㫄㫊㪀
㪘㪺㪺㪅㩿㫄㪆㫊
㪉
㪀
㪚㪸㫉㫉㫀㪸㪾㪼㩷㪻㪼㫍㫀㪺㪼㪈
㪚㪸㫉㫉㫀㪸㪾㪼㩷㪻㪼㫍㫀㪺㪼㪉
㪚㪸㫉㫉㫀㪸㪾㪼㩷㪻㪼㫍㫀㪺㪼㪊
㪚㪸㫉
Figure 5: Comparison of seating surface acceleration of a
car and a carriage device.
The sudden stop experiment was carried out and the
seating surface acceleration was measured by an ac-
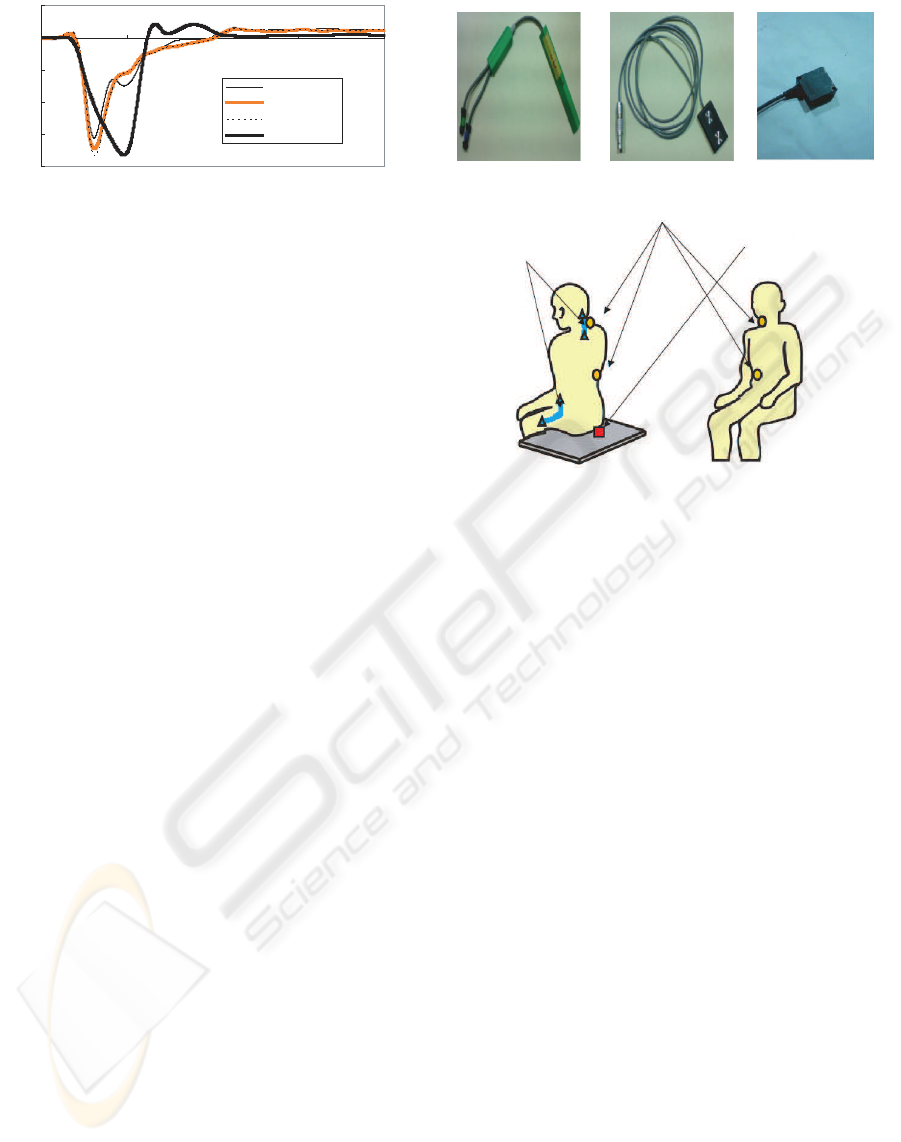
celerometer. A tensimeter was attached to the seatbelt
to measure the tension of the seatbelt. The trunk an-
gle, the cervical angle were measured by a goniome-
ter. The myoelectric potential of the sternocleidomas-
toid, the splenius, the abdominal and the muscle of
the back were measured by a myoelectric potential
sensor. Myoelectric potential sensors were attached
to the sternocleidomastoid, the splenius, the abdomi-
nal and the back muscles. To measure the sternoclei-
domastoid muscle, a myoelectric sensor was attached
between the sternoclavicularis and mastoid. To mea-
sure the splenius muscle, a myoelectric sensor was
attached one centimeter away from the fifth cervical
vertebra. To measure the abdominal muscle, a my-
oelectric sensor was attached three centimeters away
from the navel. To measure the back muscle, a my-
oelectric sensor was attached three centimeters away
from the fifth lumbar vertebra. Fig.6 shows the loca-
tion to attach the myoelectric sensors and goniome-
ters.
4 SIMULATION
4.1 Method
The muscle and physical parameters are need to be
determined in the muscle reflection model. The first
crash experiment was performed at a low acceleration
to obtain the human muscle parameters. Both the ex-
periment and the simulation results of the myoelectric
potential were matched to determine the human mus-
cle parameters(k, b,c, a
0
in Eq(7)). In addition to de-
termining the muscle parameter, another crash experi-
ment was performed at a high acceleration in order to
evaluate muscle reflection model. The human phys-
ical parameters(height, weight) were measured. The
trunk and cervical angle were simulated by Runge-
Kutta method which based on parameters obtained.
Input was the seating surface acceleration (A
x0
) and
(a)
(b)
(c)
(c)Accelerometer(b)Myoelectricsensor(a)Goniometer
(a)
(b)
(c)
(c)Accelerometer(b)Myoelectricsensor(a)Goniometer
Figure 6: Location to attach the myoelectric sensors, ac-
celerometers and goniometers.
outputs were the trunk and cervical angle and the my-
oelectric potential of measuring part.
4.2 Result
The relationship between simulation and experimen-
tal results of the trunk angle without/with seatbelt
is shown in Fig.7 and Fig.8. The relationship be-
tween simulation and experimental results of the my-
oelectric potential of the back without/with seatbelt is
shown in Fig.9 and Fig.10. Fig.7(a), (b), (c) and (d)
show that the trunk angle increases around 400ms and
returns to 0 degree. And, Fig.8(a’), (b’), (c’) and (d’)
show that trunk angle doesn’t incline. Therefore, the
simulation results of trunk angle without/with seat-
belt are similar to the experiment results in every sub-
ject. Fig.9(a), (b), (c) and (d) and Fig.10(a’), (b’),
(c’) and (d’) show that the simulation and experimen-
tal results of myoelectric potential increase around
400ms and return to 0 degree. And the peak time
of both results of myoelectric potential is matched.
Therefore, the motion and the muscle reflection of
disabled subjects could be simulated by the muscle
reflection model without/with seatbelt. And Fig.9(c),
(d) and Fig.10(c’), (d’) show that the muscle reflec-
tion of right/left hemiplegia subjects without seatbelt
is larger than that of using seatbelt.
COMPUTATIONAL MUSCLE REFLEX MODEL OF WHEELCHAIR USERS TRAVELING IN MOTOR VEHICLES -
Evaluation of the Motion and the Myoelectric Potential of People with Disabilities
83

㩿㪸㪀㪥㫆㫉㫄㪸㫃
㪄㪉㪇
㪇
㪉㪇
㪋㪇
㪇 㪌㪇㪇 㪈㪇㪇㪇 㪈㪌㪇㪇 㪉㪇㪇㪇
㪫㫀㫄㪼㩿㫄㫊㪀
㪘㫅㪾㫃㪼㩿㪻㪼㪾㪀
㪪㫀㫄㫌㫃㪸㫋㫀㫆㫅
㪜㫏㫇㪼㫉㫀㫄㪼㫅㫋
㩿㪹㪀㪨㫌㪸㪻㫉㫀㫇㫃㪼㪾㫀㪸
㪄㪉㪇
㪇
㪉㪇
㪋㪇
㪇 㪌㪇㪇 㪈㪇㪇㪇 㪈㪌㪇㪇 㪉㪇㪇㪇
㪫㫀㫄㪼㩿㫄㫊㪀
㪘㫅㪾㫃㪼㩿㪻㪼㪾㪀
㪪㫀㫄㫌㫃㪸㫋㫀㫆㫅
㪜㫏㫇㪼㫉㫀㫄㪼㫅㫋
㩿㪺㪀㪩㫀㪾㪿㫋㩷㪿㪼㫄㫀㫇㫃㪼㪾㫀㪸
㪄㪉㪇
㪇
㪉㪇
㪋㪇
㪇 㪌㪇㪇 㪈㪇㪇㪇 㪈㪌㪇㪇 㪉㪇㪇㪇
㪫㫀㫄㪼㩿㫄㫊㪀
㪘㫅㪾㫃㪼㩿㪻㪼㪾㪀
㪪㫀㫄㫌㫃㪸㫋㫀㫆㫅
㪜㫏㫇㪼㫉㫀㫄㪼㫅㫋
㩿㪻㪀㪣㪼㪽㫋㩷㪿㪼㫄㫀㫇㫃㪼㪾㫀㪸
㪄㪉㪇
㪇
㪉㪇
㪋㪇
㪇 㪌㪇㪇 㪈㪇㪇㪇 㪈㪌㪇㪇 㪉㪇㪇㪇
㪫㫀㫄㪼㩿㫄㫊㪀
㪘㫅㪾㫃㪼㩿㪻㪼㪾㪀
㪪㫀㫄㫌㫃㪸㫋㫀㫆㫅
㪜㫏㫇㪼㫉㫀㫄㪼㫅㫋
Figure 7: Comparison of the result of computer simulation
with crash experiment in measuring of trunk angle without
seatbelt.
4.3 The Calculation of the Seatbelt
Tension
The tension of a seatbelt and horizontal displacement
of the subjects were simulated in order to evaluate the
effectiveness of a seatbelt when the car stops sud-
denly. The acceleration change by sudden stop of
the carriage device in the experiment is shown in
Fig.11(a). The comparison of the tension of the seat-
belt between simulation and experiment is shown in
Fig.11(b).
㩿㪸㩾㪀㪥㫆㫉㫄㪸㫃
㪄㪉㪇
㪇
㪉㪇
㪋㪇
㪇 㪌㪇㪇 㪈㪇㪇㪇 㪈㪌㪇㪇 㪉㪇㪇㪇
㪫㫀㫄㪼㩿㫄㫊㪀
㪘㫅㪾㫃㪼㩿㪻㪼㪾㪀
㪪㫀㫄㫌㫃㪸㫋㫀㫆㫅
㪜㫏㫇㪼㫉㫀㫄㪼㫅㫋
㩿㪹㩾㪀㪨㫌㪸㪻㫉㫀㫇㫃㪼㪾㫀㪸
㪄㪉㪇
㪇
㪉㪇
㪋㪇
㪇 㪌㪇㪇 㪈㪇㪇㪇 㪈㪌㪇㪇 㪉㪇㪇㪇
㪫㫀㫄㪼㩿㫄㫊㪀
㪘㫅㪾㫃㪼㩿㪻㪼㪾㪀
㪪㫀㫄㫌㫃㪸㫋㫀㫆㫅
㪜㫏㫇㪼㫉㫀㫄㪼㫅㫋
㩿㪺㩾㪀㪩㫀㪾㪿㫋㩷㪿㪼㫄㫀㫇㫃㪼㪾㫀㪸
㪄㪉㪇
㪇
㪉㪇
㪋㪇
㪇 㪌㪇㪇 㪈㪇㪇㪇 㪈㪌㪇㪇 㪉㪇㪇㪇
㪫㫀㫄㪼㩿㫄㫊㪀
㪘㫅㪾㫃㪼㩿㪻㪼㪾㪀
㪪㫀㫄㫌㫃㪸㫋㫀㫆㫅
㪜㫏㫇㪼㫉㫀㫄㪼㫅㫋
㩿㪻㩾㪀㪣㪼㪽㫋㩷㪿㪼㫄㫀㫇㫃㪼㪾㫀㪸
㪄㪉㪇
㪇
㪉㪇
㪋㪇
㪇 㪌㪇㪇 㪈㪇㪇㪇 㪈㪌㪇㪇 㪉㪇㪇㪇
㪫㫀㫄㪼㩿㫄㫊㪀
㪘㫅㪾㫃㪼㩿㪻㪼㪾㪀
㪪㫀㫄㫌㫃㪸㫋㫀㫆㫅
㪜㫏㫇㪼㫉㫀㫄㪼㫅㫋
Figure 8: Comparison of the result of computer simula-
tion with crash experiment in measuring of trunk angle with
seatbelt.
Although Fig.11(b) indicated that the maximum ten-
sion of the simulation matched that of the experiment,
the simulation result increased sharply around 400ms.
This indicated that the simulation result didn’t take
time lag into account until the seatbelt started to pull
the human body.
BIOSIGNALS 2009 - International Conference on Bio-inspired Systems and Signal Processing
84

㩿㪸㪀㪥㫆㫉㫄㪸㫃
㪇
㪇㪅㪉
㪇㪅㪋
㪇㪅㪍
㪇㪅㪏
㪈
㪇 㪌㪇㪇 㪈㪇㪇㪇 㪈㪌㪇㪇 㪉㪇㪇㪇
㪫㫀㫄㪼㩿㫄㫊㪀
㩼㪤㪭㪚
㪪㫀㫄㫌㫃㪸㫋㫀㫆㫅
㪜㫏㫇㪼㫉㫀㫄㪼㫅㫋
㩿㪹㪀㪨㫌㪸㪻㫉㫀㫇㫃㪼㪾㫀㪸
㪇
㪇㪅㪉
㪇㪅㪋
㪇㪅㪍
㪇㪅㪏
㪈
㪇 㪌㪇㪇 㪈㪇㪇㪇 㪈㪌㪇㪇 㪉㪇㪇㪇
㪫㫀㫄㪼㩿㫄㫊㪀
㩼㪤㪭㪚
㪪㫀㫄㫌㫃㪸㫋㫀㫆㫅
㪜㫏㫇㪼㫉㫀㫄㪼㫅㫋
㩿㪺㪀㪩㫀㪾㪿㫋㩷㪿㪼㫄㫀㫇㫃㪼㪾㫀㪸
㪇
㪇㪅㪉
㪇㪅㪋
㪇㪅㪍
㪇㪅㪏
㪈
㪇 㪌㪇㪇 㪈㪇㪇㪇 㪈㪌㪇㪇 㪉㪇㪇㪇
㪫㫀㫄㪼㩿㫄㫊㪀
㩼㪤㪭㪚
㪪㫀㫄㫌㫃㪸㫋㫀㫆㫅
㪜㫏㫇㪼㫉㫀㫄㪼㫅㫋
㩿㪻㪀㪣㪼㪽㫋㩷㪿㪼㫄㫀㫇㫃㪼㪾㫀㪸
㪇
㪇㪅㪉
㪇㪅㪋
㪇㪅㪍
㪇㪅㪏
㪈
㪇 㪌㪇㪇 㪈㪇㪇㪇 㪈㪌㪇㪇 㪉㪇㪇㪇
㪫㫀㫄㪼㩿㫄㫊㪀
㩼㪤㪭㪚
㪪㫀㫄㫌㫃㪸㫋㫀㫆㫅
㪜㫏㫇㪼㫉㫀㫄㪼㫅㫋
Figure 9: Comparison of the result of computer simulation
with crash experiment in measuring of myoelectric potential
of the back without seatbelt.
5 DISCUSSION
Fig.7 and Fig.8 show that the trunk angle of each
subject without seatbelt increases more than that of
each subject with seatbelt, because the seatbelt works
effectively. Fig.10(a’) shows that the normal sub-
ject uses his muscle to control his trunk angle when
he is wearing a seatbelt. Fig.9(b), (c) and (d) and
Fig.10(b’), (c’) and (d’) show that the muscle reflec-
tion of disabled subjects with seatbelt is stronger than
that without seatbelt. This indicated that the trunk an-
gle of disabled subjects is restored by the seatbelt in-
㩿㪸㩾㪀㪥㫆㫉㫄㪸㫃
㪇
㪇㪅㪉
㪇㪅㪋
㪇㪅㪍
㪇㪅㪏
㪈
㪇 㪌㪇㪇 㪈㪇㪇㪇 㪈㪌㪇㪇 㪉㪇㪇㪇
㪫㫀㫄㪼㩿㫄㫊㪀
㩼㪤㪭㪚
㪪㫀㫄㫌㫃㪸㫋㫀㫆㫅
㪜㫏㫇㪼㫉㫀㫄㪼㫅㫋
㩿㪹㩾㪀㪨㫌㪸㪻㫉㫀㫇㫃㪼㪾㫀㪸
㪇
㪇㪅㪉
㪇㪅㪋
㪇㪅㪍
㪇㪅㪏
㪈
㪇 㪌㪇㪇 㪈㪇㪇㪇 㪈㪌㪇㪇 㪉㪇㪇㪇
㪫㫀㫄㪼㩿㫄㫊㪀
㩼㪤㪭㪚
㪪㫀㫄㫌㫃㪸㫋㫀㫆㫅
㪜㫏㫇㪼㫉㫀㫄㪼㫅㫋
㩿㪺㩾㪀㪩㫀㪾㪿㫋㩷㪿㪼㫄㫀㫇㫃㪼㪾㫀㪸
㪇
㪇㪅㪉
㪇㪅㪋
㪇㪅㪍
㪇㪅㪏
㪈
㪇 㪌㪇㪇 㪈㪇㪇㪇 㪈㪌㪇㪇 㪉㪇㪇㪇
㪫㫀㫄㪼㩿㫄㫊㪀
㩼㪤㪭㪚
㪪㫀㫄㫌㫃㪸㫋㫀㫆㫅
㪜㫏㫇㪼㫉㫀㫄㪼㫅㫋
㩿㪻㩾㪀㪣㪼㪽㫋㩷㪿㪼㫄㫀㫇㫃㪼㪾㫀㪸
㪇
㪇㪅㪉
㪇㪅㪋
㪇㪅㪍
㪇㪅㪏
㪈
㪇 㪌㪇㪇 㪈㪇㪇㪇 㪈㪌㪇㪇 㪉㪇㪇㪇
㪫㫀㫄㪼㩿㫄㫊㪀
㩼㪤㪭㪚
㪪㫀㫄㫌㫃㪸㫋㫀㫆㫅
㪜㫏㫇㪼㫉㫀㫄㪼㫅㫋
Figure 10: Comparison of the result of computer simulation
with crash experiment in measuring of myoelectric potential
of the back with seatbelt.
stead of muscle reflection. When disabled subjects
don’t wear seatbelt, they need to use their muscles
more than normal subject. Therefore using a seatbelt
is more important for people with disabilities than in
the case of normal people.
Next, the simulation results are focused. The motion
and the muscle reflection pattern in each subject are
similar. The experiment results can be simulated by
the model based on muscle reflection. The muscle
reflection of people with disabilities responds more
strongly than that of normal people in the case without
a seatbelt. Therefore, people with disabilities experi-
COMPUTATIONAL MUSCLE REFLEX MODEL OF WHEELCHAIR USERS TRAVELING IN MOTOR VEHICLES -
Evaluation of the Motion and the Myoelectric Potential of People with Disabilities
85

㩿㪸㪀㪫㪿㪼㩷㪸㪺㪺㪼㫃㪼㫉㪸㫋㫀㫆㫅㩷㫆㪽㩷㫋㪿㪼㩷㪺㪸㫉㫉㫀㪸㪾㪼㩷㪻㪼㫍㫀㪺㪼
㪄㪉㪇
㪄㪈㪌
㪄㪈㪇
㪄㪌
㪇
㪌
㪇 㪌㪇㪇 㪈㪇㪇㪇 㪈㪌㪇㪇 㪉㪇㪇㪇
㪫㫀㫄㪼㩿㫄㫊㪀
㪘㪺㪺㪼㫃㪼㫉㪸㫋㫀㫆㫅㩿㫄㪆㫊
㪉
㪀
㩿㪹㪀㪫㪿㪼㩷㫋㪼㫅㫊㫀㫆㫅㩷㫆㪽㩷㫋㪿㪼㩷㫊㪼㪸㫋㪹㪼㫃㫋
㪇
㪌㪇㪇
㪈㪇㪇㪇
㪇 㪌㪇㪇 㪈㪇㪇㪇 㪈㪌㪇㪇 㪉㪇㪇㪇
㪫㫀㫄㪼㩿㫄㫊㪀
㪝㫆㫉㪺㪼㩿㪥㪀
㪪㫀㫄㫌㫃㪸㫋㫀㫆㫅
㪜㫏㫇㪼㫉㫀㫄㪼㫅㫋
Figure 11: The comparison of the tension of a seatbelt of
simulation and experiment result.
ence stronger physical burden than others do. Even
though a serious traffic accident doesn’t occur, a seat-
belt is a useful tool for wheelchair users because it
helps to control their movement instead of using their
muscles while traveling in a motor vehicle.
6 CONCLUSIONS
In this study, a human motion model in a wheelchair
traveling in a motor vehicle was developed. The
model was expressed the motion of subjects with dis-
abilities by using muscle parameters of each subject.
The motion of subjects with disabilities can almost be
simulated by this model. The simulation results show
that the a seatbelt help to control the motion and the
muscle activity of subjects with disabilities. However,
the seatbelt and muscle reflection model couldn’t sim-
ulate accurately. The results show that disabled peo-
ple need to wear a seatbelt more than in the case of
normal people.
In the future, relationship between myoelectric poten-
tial and muscle force will be investigated by funda-
mental experiments, improvement of myoelectric po-
tential’s equation and optimal calculation of muscle
parameters in order to make safety guideline which
are acceptable for people with disabilities.
ACKNOWLEDGEMENTS
This work is supported by Mr.Shigeki Abe, Life sup-
port co ltd. and this work was supported by the Grant-
in-Aid for Scientific Research (B) from the Japan So-
ciety for the Promotion of Science.
REFERENCES
ANSI/RESNA (2002). Wheelchairs used in motor vehicle
transportation. ANSI/RESNA.
Aomura, S. (2007). Modeling to impact effect for disabled
people on the wheelchair during vehicle driving. Jour-
nal of Japan Society of Mechanical Engineers.
Bertocci, G. (1999). Computer simulation and sled test val-
idation of a powerbase wheelchair and occupant sub-
jected to frontal crash conditions. IEEE TRANSAC-
TIONS ON REHABILITATION ENGINEERING.
Bertocci, G. (2000). Development of a wheelchair occupant
injury risk assessment method and its application in
the investigation of wheelchair securement point influ-
ence on frontal crash safety. IEEE TRANSACTIONS
ON REHABILITATION ENGINEERING.
Bertocci, G. (2001). Wheelchairs used as motor vehicle
seats: seat loading in frontal impact sled testing. Med-
ical Engineering and Physics.
Hase, K. (2002). Biomechanics of rowing(ii .a control
model for the simulation study of rowing and other
human movement). Japan Society of Mechanical En-
gineers.
Luca, D. (1979). Physiology and mathematics of myoelec-
tric signals. IEEE Transactions on Biomedical Engi-
neering.
Mooreroft, D. (1999). Computational model of the pregnant
occupant: Predicting the risk of injury in automobile
crashes. American Journal of Obstetrics and Gynecol-
ogy.
Ogihara, N. (2000). Spontaneous generation of anti-
gravitational arm motion based on anatomical con-
strain of the human body. Proc. AMAM (Adaptive
Motion in Animals and Machines) Montreal.
Uenishi, K. (2005). Dynamic model for car occupants in
head-on collisions. Jornal of Japan Society of Me-
chanical Engineers.
W.E.Fisher (1987). Development of an australian standard
for wheelchair occupant restraint assemblies for mo-
tor vehicles. Journal of Rehabilitation Reserch and
Development.
BIOSIGNALS 2009 - International Conference on Bio-inspired Systems and Signal Processing
86
