
INTRA-PATIENT REGISTRATION METHODS
FOR THORACIC CT EXAMS
José Silvestre Silva
Departamento de Física, Faculdade de Ciências e Tecnologia,Universidade de Coimbra, Portugal
Centro de Instrumentação, Faculdade de Ciências e Tecnologia,Universidade de Coimbra, Portugal
João Cancela
Departamento de Física, Faculdade de Ciências e Tecnologia,Universidade de Coimbra, Portugal
Luísa Teixeira
Clínica Universitária de Imagiologia dos Hospitais da Universidade de Coimbra, Portugal
Keywords: Medical Image Analysis, Image Registration, Lung Tumours, Computed Tomography.
Abstract: Now-a-days CT scanners provide detailed morphological information of pulmonary structures, with great
importance to the diagnostic and follow-up of oncological diseases. When a patient with lung cancer is
submitted to several CT exams during a period of time; these exams need an appropriate registration to
quantify or visualize the tumour’s evolution. We propose a new method for 3D intra-patient registration of
thoracic CT exams and compare its results with several 3D registration methods. The performance of these
registration methods is analysed, computing several normalized figures of merit; we also explore these
metrics to check which is more sensible to changes in CT exams due to the presence of lung tumours. The
results with several cases of intra-patient, intra-modality registration show that the proposed method
provides an accurate registration which is needed for the quantitative tracking of lesions that may effectively
assist the follow-up process of oncological patients.
1 INTRODUCTION
Modern high resolution Computed Tomography
scanners offer more diagnostic options and a better
diagnostic quality. Consequently, it will also
increase the time needed for data reading by the
radiologist. Therefore, computer aid is necessary in
order to increase the level of efficiency and quality
in the diagnostic workflow.
Image registration geometrically aligns two
images: the reference and sensed images. To register
two images it is necessary to find a transformation
so that each pixel in the first image can be mapped
to a pixel in the second (Brown, 1992) (Blaffert &
Wiemker, 2004). The image registration is used in
several clinical scenarios. For instance, consider two
images taken of a patient using different medical
modalities or comparing two CT exams from a
patient, to identify the differences between the two
images in a follow-up study of an oncological
patient. Although this identification can be done by
the radiologist, there is always the possibility that
small, but essential, features could be missed
(Brown, 1992).
In the literature, it is found some work done in
this area. El-Baz (El-Baz, Yuksel, Elshazly, &
Farag, 2005) developed an automatic approach for
the early detection of lung nodules that may lead to
lung cancer. This approach involves performing
rigid registration and then a non-rigid registration to
compensate the lung deformation due to the heart
beats and respiration of the patient; however this
method cannot handle large deformations.
Matsopoulos (Matsopoulos, Mouravliansky,
Asvestas, Delibasis, & Kouloulias, 2002) proposed
an automatic elastic registration scheme applied on
thoracic CT exams of patients diagnosed with non-
small cell lung cancer.
285
Silvestre Silva J., Cancela J. and Teixeira L. (2009).
INTRA-PATIENT REGISTRATION METHODS FOR THORACIC CT EXAMS .
In Proceedings of the International Conference on Bio-inspired Systems and Signal Processing, pages 285-290
DOI: 10.5220/0001538002850290
Copyright
c
SciTePress

Volumetric warping and registration of CT lung
volumes have been investigated by Li (Li,
Christensen, Dill, Hoffman, & Reinhardt, 2002),
whose approach uses point correspondence of
landmarks that are expanded over the entire volume
by means of an iterative method. Although this
method has shown good results for mapping lung
deformation due to respiration, it requires the
manual registration of landmarks.
Betke (Betke, Hong, Thomas, Prince, & Ko,
2003) developed an automated method for
registering CT images of the chest; it detected
anatomical landmarks: the trachea, sternum and
spine, then he used an iterative lung surface
registration based on minimizing Euclidean
distances. The locations of the pulmonary vessel
branch points and nodules were manually defined.
Blaffert (Blaffert & Wiemker, 2004) studied the
precision and computation time of a rigid body using
an affine and a spline based elastic registration
approach on the full data volume; he compared the
results to an affine registration that was preceded by
a segmentation of the lung.
Boldea (Boldea, Sarrut, & Carrie, 2005)
investigated the deformable registration methods for
a breath-hold reproducibility study in radiotherapy,
analysing internal lung residual motion between
several 3D CT scans taken from the same patient, at
the same level of the breathing cycle.
West (West, Maurer, & Dooley, 2005) examined
the problem of deformable registration of the
abdomen and was interested in modelling respiratory
motion of abdominal organs, because the
deformation of the lungs during the respiratory cycle
can lead to the movement of others organs (liver,
kidney, etc.); he used twenty-one landmarks selected
manually.
Chambon (Chambon et al., 2007) presented a
CT-PET landmark-based registration method that
uses a breathing model to guarantee physiologically
plausible deformations.
Fung (Fung, Wong, Cheng, Grimm, & Uematsu,
2005) compared two image fusion techniques for the
localization of patient position during radiation
release for cancer patients.
Tang (Tang, Hamarneh, & Celler, 2006)
presented an automatic and accurate technique for
3D registration of SPECT and CT, which allowed
the attenuation correction of SPECT images and the
fusion of the anatomic details from CT and the
functional information from SPECT.
Ruan (Ruan, Fessler, Robserson, Balter, &
Kessler, 2007) studied a method that takes into
account different types of tissues, especially bone, in
non-rigid registration. Chen (Chen, Varley, Shark,
Shentall, & Kirby, 2007) presented a 3D-2D image
registration algorithm for pre-treatment validation in
radiotherapy.
In the present work, we propose a methodology
for the 3D intra-patient registration of thoracic CT
exams. We compare performances analysing the
processing time and the values of similarity metrics
for each method. We also studied the behaviour of
several normalized similarity metrics in the presence
of pulmonary tumours in oncological patients.
2 METHOD
In this paper, we present a method for the
registration of pulmonary CT exams and compare its
performance with traditional registration method and
also with two optimised registration methods. Also
in this work, we search for the best metric, sensible
to changes in CT exams, due to the presence of lung
tumours.
2.1 Pre-processing
In the high resolution CT exams, the images are
sensitive to noise, especially in the extra-thoracic
region, where there is air. As noise can contribute
negatively to the lung’s segmentation, before any
processing, and after comparing several denoising
filters (J. S. Silva, Silva, & Santos, 2003), the noise
is attenuated using a geometric mean filter (Sonka,
Hlavac, & Boyle, 1998).
The pulmonary regions are identified using a
previous developed (A. Silva, Silva, Santos, &
Ferreira, 2001) (J. S. S. Silva, 2005) and validated
algorithm (Santos, Ferreira, Silva, Silva, & Teixeira,
2004) producing always one contour for each lung.
This algorithm uses information from the CT image
histogram and, with a chain of morphological
operations, identifies the left and right lung contours.
Even when the lungs are visually merged, two
contours are always identified, defining the frontier
of left and right lungs. After pulmonary
segmentation, all binary slices are joined to create
one 3D pulmonary image.
Finally, in this pre-alignment step, it is computed
the mass center of both 3D CT exams and performed
a translation on the second exam, in order to both
mass centers become coincident.
BIOSIGNALS 2009 - International Conference on Bio-inspired Systems and Signal Processing
286

2.2 Affine Registration
The registration can be understood as the
determination of spatial alignment between images.
For the present method, we consider affine
transformations, as the only relevant transformation
(Blaffert & Wiemker, 2004).
2.2.1 Transformations
We defined the following transformation matrix: T
for translation on x, y ,z; R
x
, R
y
, R
z
for rotation over
3 axis, C
xy
, C
xz
and C
yz
for shearing on planes xy, xz
and yz and S for scaling. The various transformation
matrices are multiplied among them to obtain a
global matrix, in order to process all voxels from the
CT exam:
SCyzCxzCxyRzRyRxTGLOBAL ×××
×
×××=
(1)
In traditional 3D registration methods, all
translations are iteratively searched, and for each
translation all rotations are searched, and so on;
processing a 3D image becomes a very long process.
In order to overcome this limitation, we propose a
registration method that sequentially performs each
transformation.
In this proposed method, the first step is the
search for the best translation, then holding this
value; it searches for the best rotation over x axis.
Holding these two best values; it searches for the
best rotation over y axis, and so on, obtaining the
best values for each transformation in a much faster
approach than in traditional 3D registration methods.
In the second step, it uses the best values found in
the previous step as starting point, and then repeats
the same procedure described in the first step,
searching for new best values.
2.2.2 Boundaries
Setting boundaries for transformation is very
important to reduce the processing time. For a CT
exam that has been correctly acquired, it should not
have a displacement of more than ¼ of width of the
exam, and the patient body should not have a
rotating higher that 15º on the table, otherwise the
examination is considered inappropriate, because the
anatomical structures may exceed the limits of the
image; these are the limits used for the
transformations.
To enhance the speed of our method, we start by
computing the width of the CT exam and use 1/8 of
the width as the step for searching the best
translation, over the x, y and z axis in a range
from −¼ of the exam width, to +¼ of the exam
width. After searching for these axes, the best value
is found comparing all values computed for the
similarity metric.
The best translation is identified and using this
value as the starting point, a new search is
performed in a range from −1/8 of the exam width,
to +1/8 of the exam width centred at the starting
point, using a step of 1/16 of the exam width, which
is half of the previous used step. This procedure is
repeated until the step reaches the unit.
Then we search for the best rotation, following a
similar procedure used for translation. Holding the
translation best value found, we search for the best
rotation, along the 3 rotation axis, in a range of
[−15º; +15º] with a step of 7.5º. After identifying the
best rotation, we use this value as the starting point
and search for a new best value in a range of ± 7.5º,
centred at the starting point, with a step of 7.5º/2.
This procedure is repeated until the rotation step
reaches the value of one degree. Similar procedures
are used for scale and for shear.
2.3 Metrics
We used several normalized similarity metrics, also
known as figures of merit to quantify the differences
between the reference exam and the exam under
analysis. These three metrics: Sum of the Absolute
Differences (SAD), Correlation (R) and Normalized
Mutual Information (NMI) have values between 0
(for two different images) and 1 (for two coincident
images) (Fitzpatrick, Hill, & Calvin R. Maurer,
2000) (Hill, Batchelor, Holden, & Hawkes, 2001)
(Pratt, 2001). The Mutual Information (MI) metric is
shown to help computing the NMI.
∑∑∑
−−−−−=
X
i
Y
j
Z
k
oknjmiBkjiA
N
BASAD ),,(),,(
1
1),(
(2)
∑∑ ∑∑∑∑
∑∑∑
−−−×
−−−×
=
X
i
Y
j
X
i
Y
j
Z
k
Z
k
X
i
Y
j
Z
k
oknjmiBkjiA
oknjmiBkjiA
R
22
),,(),,(
),,(),,(
(3)
∑∑
∈∈
=
AaBb
BA
AB
AB
ba
ba
baBAMI
)()(
),(
log),(),(
ρρ
ρ
ρ
(4)
)()(
),(2
),(
BHAH
BAMI
BANMI
+
=
with
[]
∑
∈
−=
Aa
AA
aaAH )(log)()(
ρρ
(5)
where, A and B are images; N is a normalization
coefficient; i, j and k are the coordinates on the
image; m, n and o are the displacement values to the
reference image; ρ
AB
(a,b) is the joint probability of
INTRA-PATIENT REGISTRATION METHODS FOR THORACIC CT EXAMS
287

the image and ρ
A
(a), ρ
B
(b) are the probability of
images A and B, respectively.
2.4 Other Registration Methods
Two registration methods, using the Simplex
algorithm and the Patter Search algorithm, were also
implemented to compare their performance with the
proposed method.
The Nelder-Mead Simplex algorithm is a direct
search method for multidimensional unconstrained
minimization. Without any derivative information, a
scalar-valued nonlinear function of n real variables
using only function values is minimized. The
Nelder-Mead algorithm preserves at each stage a
nondegenerate simplex, a volume different from
zero in n dimensions which is the convex surface of
n+1 vertices. This method starts with a simplex,
specified by its n + 1 vertices and the related
function values for each iteration. At least one test
point is calculated, as well as their function values,
and the iteration ends with the levels sets delimited
(Lagarias, Reeds, Wright, & Wright, 1998).
The Pattern Search algorithm is also a direct
search method and uses the function from a
prearranged pattern of points fixed around the
current best point, using shifts that guarantee
determined minimal conditions in order to ensure the
strong performance of the method. This process is
repeated with the pattern centred on the new best
point whenever certain minimal conditions are
ensured. In other words, the reduction of the size of
the pattern occurs and the function is sampled once
again. The goal of the Pattern Search is sampled at
set points which are broader than in the Simplex-
based methods (Torczon, 1997) (Lewis & Torczon,
2002).
3 RESULTS AND DISCUSSION
In this section, we present the results from the
comparison of our method and three other methods:
the traditional registration method and two other
methods with optimization algorithms: the Simplex
algorithm and the Pattern Search algorithm.
In a second step we used exams from an arbitrary
patient and perform the registration of all exams, to
analyse the behaviour of normalized similarity
metrics.
The results of all registration methods were
computed on a desktop computer Intel Core 2 Quad,
4GB RAM, using Matlab.
Our dataset has 40 CT exams from 10 patients,
each exam has about 100 sections, with 512×512
pixels, a resolution of 0.781×0.781×5mm
3
and each
section is adjacent to its neighbours.
3.1 Comparing Registration Methods
We compare the results of several 3D registration
methods, performing the intra-patient registration of
two exams, acquired with one month interval.
In table 1 it is shown the results of 3D intra-
patient registration of pulmonary CT exams,
downsampled to 128×128×n (where n is the original
number of sections), which include correlation
values (initial value, after pre-processing /
preliminary alignment based on mass center, final
value), processing time and the number of iterations.
Table 1: Correlation values: registration of two exams
from patient A.
(Patient A) Correlation values Time No. of
Method: Initial Pre-align Final (min) iterations
Traditional 0.854 0.857 0.939 1830 21870
Our method 0.854 0.857 0.904 20 234
Pattern Search 0.854 0.857 0.929 116 1385
Simplex 0.854 0.857 0.878 12 128
From table 1, we see that the processing time of
our method and Simplex method are much lower
than the other two methods, which suggests that our
method is a fast 3D registration technique, even
when compared with a method that uses an
optimization algorithm (Pattern Search method). We
also observe that the best correlation values are
obtained with the Pattern Search method (and with
traditional method) and the worst value, with the
Simplex Algorithm. So, the traditional method, due
to the long processing time, is rejected.
In table 2 it is shown the results of 3D intra-
patient registration of pulmonary CT exams,
downsampled to 64×64×n (as described for table 1)
and the initial / pre-processing / final values, for
Normalized Mutual Information.
Table 2: Normalized Mutual Information values:
registration of two exams from patient B.
(Patient B) Normalized Mutual Infor. Time No. of
Method: Initial Pre-align Final (min) iterations
Traditional 0.114 0.628 0.799 1050 21870
Our method 0.114 0.628 0.705 12 234
Pattern Search 0.114 0.628 0.796 45 1579
Simplex 0.114 0.628 0.681 15 286
In table 2, we see that our method and the
Simplex method accomplish the lower processing
BIOSIGNALS 2009 - International Conference on Bio-inspired Systems and Signal Processing
288
time. However, the normalized mutual information
achieved by Simplex method is worse than the value
obtained by our method, which suggests that our
method is one of the best, in comparison with the
three methods.
3.2 Metrics in Tumour Discrimination
Using six exams (A1, A2, A3, A4 A5 and A6)
acquired during six months, one exam in each
month, for the patient A (patient with lung cancer
undergoing intensive therapy), we performed the
registration using our method, of first exam A1 with
second exam A2, also the first exam A1 with third
exam A3, and so on, as shown in table 3. For each
registration, the SAD, R and NMI metrics were
computed. To reduce computational time, the exams
were downsampled to 128×128×n and the lungs
were segmented, producing 3D binary volumes,
corresponding to the pulmonary regions.
Table 3: Intra-patient registration method, using 6 CT
exams from a patient with lung cancer.
SAD
A1 w/ A2 A1 w/ A3 A1 w/ A4 A1 w/ A5 A1 w/ A6
Initial 0.937 0.891 0.924 0.817 0.900
Pre-align 0.939 0.923 0.949 0.936 0.929
Final 0.961 0.956 0.969 0.961 0.956
R
A1 w/ A2 A1 w/ A3 A1 w/ A4 A1 w/ A5 A1 w/ A6
Initial 0.854 0.742 0.831 0.598 0.766
Pre-align 0.857 0.817 0.886 0.860 0.834
Final 0.903 0.891 0.930 0.914 0.896
NMI
A1 w/ A2 A1 w/ A3 A1 w/ A4 A1 w/ A5 A1 w/ A6
Initial 0.588 0.387 0.525 0.191 0.417
Pre-align 0.594 0.512 0.640 0.584 0.537
Final 0.692 0.665 0.752 0.708 0.670
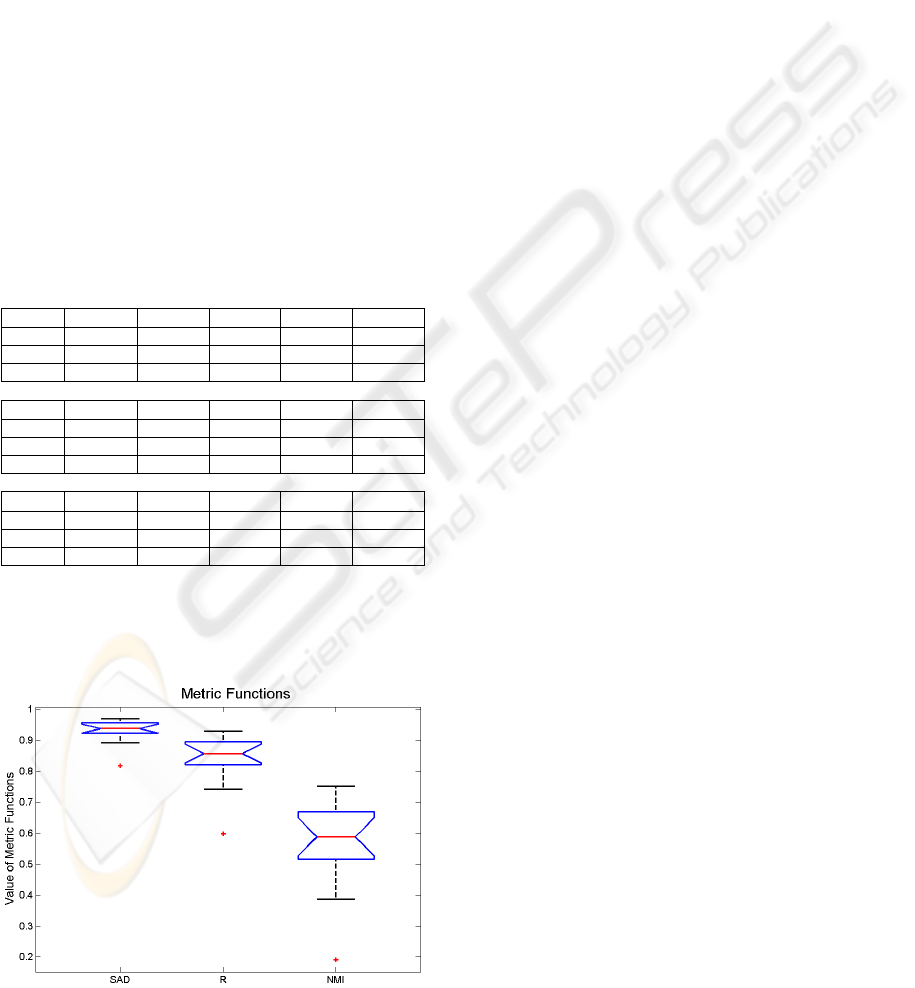
Using the data from table 3, we create a group
for each metric and produce a box-plot graphic, to
observe the dispersion of metric values.
Figure 1: Dispersion values of similarity metrics.
From figure 1, and discarding the three outlier
points, we see that SAD has the lower dispersion
interval (values from 0.891 to 0.969) and the NMI
has the higher dispersion interval (values from 0.387
to 0.752) which suggests that NMI is more sensible
to the presence of tumours.
These results were confirmed with results from
intra-patient registration of CT exams, using other
patients with lung cancer.
4 CONCLUSIONS
In this paper, we addressed the problem of
registering volumetric pulmonary CT exams of
patients with lung cancer. We propose an automatic
3D intra-patient registration method. It starts by
segmenting the lungs and building a 3D binary
image of the pulmonary region. The centre of mass
is computed and the exams are coarsely aligned.
Then, a 3D registration is performed using a
downsampled volume from the original 3D image.
The performance of our method is compared with
the traditional registration method and also with two
optimised methods and we conclude that our method
is the best compromise between processing time and
similarity metric values.
Also, we compare the results of several
normalized similarity metrics used in the 3D
registration of CT exams and conclude that
normalized mutual information is the metric more
sensible to the changes in CT exams due to the
presence of lung tumours.
The results with several cases of intra-patient,
intra-modality registration show that this method
provides accurate registration which is needed for
the quantitative tracking of lesions that may
effectively assist the follow-up process of
oncological patients.
REFERENCES
Betke, M., Hong, H., Thomas, D., Prince, C., & Ko, J. P.
(2003). Landmark Detection in the Chest and
Registration of Lung Surfaces with an Application to
Nodule Registration. Medical Image Analysis, 7(3),
265-281.
Blaffert, T., & Wiemker, R. (2004). Comparison of
different follow-up lung registration methods with and
without segmentation. SPIE Medical Imaging 2004,
5370, 1701-1708.
Boldea, V., Sarrut, D., & Carrie, C. (2005). Comparison of
3D Dense Deformable Registration Methods for
Breath-hold Reproducibility Study in Radiotherapy.
INTRA-PATIENT REGISTRATION METHODS FOR THORACIC CT EXAMS
289

SPIE Medical Imaging: Visualization, Image-Guided
Procedures, and Display, 5747, 222-230.
Brown, L. G. (1992). A Survey of Image Registration
Techniques. ACM Computing Surveys, 24(4), 325-376.
Chambon, S., Moreno, A., Santhanam, A. P., Rolland, J.
P., Angelini, E., & Bloch, I. (2007). CT-PET
Landmark-based Lung Registration Using a Dynamic
Breathing Model. Proceedings of the 14th
International Conference on Image Analysis and
Processing (ICIAP 2007) - Volume 00, 691-696.
Chen, X., Varley, M. R., Shark, L.-K., Shentall, G. S., &
Kirby, M. C. (2007). Automatic 3D-2D image
registration using partial digitally reconstructed
radiographs along projected anatomic contours. Proc.
of International Conference on Medical Information
Visualisation - BioMedical Visualisation (MediViz
2007), 3-8.
El-Baz, A., Yuksel, S., Elshazly, S., & Farag, A. (2005).
Non-rigid registration techniques for automatic
follow-up of lung nodules. Proc. of Computer Assisted
Radiology and Surgery (CARS'05), Berlin, Germany,
1115-1120.
Fitzpatrick, J. M., Hill, D. L. G., & Calvin R. Maurer, J.
(2000). Image Registration. In M. Sonka & J. M.
Fitzpatrick (Eds.), Handbook of Medical Imaging
(Vol. 2, pp. 447 - 514): SPIE Press.
Fung, A. Y. C., Wong, J. R., Cheng, C.-W., Grimm, S. L.,
& Uematsu, M. (2005). A comparison of two image
fusion techniques in CT-on-Rails localization of
radiation delivery. Physica Medica, 21(3), 113-119.
Hill, D. L. G., Batchelor, P. G., Holden, M., & Hawkes, D.
J. (2001). Medical image registration. Physics in
Medicine and Biology, 46(3), 1- 45.
Lagarias, J. C., Reeds, J. A., Wright, M. H., & Wright, P.
E. (1998). Convergence Properties of the Nelder-Mead
Simplex Method in Low Dimensions. SIAM J. on
Optimization, 9(1), 112-147.
Lewis, R. M., & Torczon, V. (2002). A Globally
Convergent Augmented Lagrangian Pattern Search
Algorithm for Optimization with General Constraints
and Simple Bounds. SIAM J. on Optimization, 12(4),
1075-1089.
Li, B., Christensen, G. E., Dill, J., Hoffman, E. A., &
Reinhardt, J. M. (2002). 3D inter-subject warping and
registration of pulmonary CT images for a human lung
model. SPIE - Medical Imaging 2002: Physiology and
Function from Multidimensional Images, 4683, 324-
335.
Matsopoulos, G. K., Mouravliansky, N. A., Asvestas, P.
A., Delibasis, K. K., & Kouloulias, V. (2002).
Thoracic non-rigid registration combining self-
organizing maps and radial basis functions. Med Phys.,
29(2), 201-213.
Pratt, W. K. (2001). Digital Image Processing: John Wiley
& Sons, Inc.
Ruan, D., Fessler, J. A., Robserson, M., Balter, J., &
Kessler, M. (2007). Nonrigid Registration with
Regularization Incorporating Local Tissue Rigidity.
Phys. Med. Biol. (in revision).
Santos, B. S., Ferreira, C., Silva, J. S., Silva, A., &
Teixeira, L. (2004). Quantitative Evaluation of a
Pulmonary Contour Segmentation Algorithm in X-ray
Computed Tomography Images.
Academic Radiology,
11(8), 868-878.
Silva, A., Silva, J. S., Santos, B. S., & Ferreira, C. (2001).
Fast Pulmonary Contour Extraction in X-ray CT
Images: A Methodology and Quality Assessment.
SPIE - Medical Imaging 2001: Physiology and
Function from Multidimensional Images, 4321, 216-
224.
Silva, J. S., Silva, A., & Santos, B. S. (2003). Denoising
Methods in High-Resolution X-Ray Computed
Tomography. Proceedings of BioEng 2003 - 7th
Portuguese Conference on Biomedical Engineering,
59 (extended version in CD of Proceedings).
Silva, J. S. S. (2005). Segmentação Pulmonar em Estudos
de Tomografia Axial Computorizada: PhD Thesis (in
Portuguese), Universidade de Aveiro.
Sonka, M., Hlavac, V., & Boyle, R. (1998). Image
Processing, Analysis, and Machine Vision (2nd ed.):
PWS Publishing.
Tang, L., Hamarneh, G., & Celler, A. (2006). Co-
registration of Bone CT and SPECT Images Using
Mutual Information. IEEE Symposium on Signal
Processing and Information Technology, 116-121.
Torczon, V. (1997). On the Convergence of Pattern Search
Algorithms. SIAM J. on Optimization, 7(1), 1-25.
West, J. B., Maurer, C. R., & Dooley, J. R. (2005). Hybrid
point-and-intensity-based deformable registration for
abdominal CT images. Proceedings of SPIE Medical
Imaging 2005, 5747, 204-211.
BIOSIGNALS 2009 - International Conference on Bio-inspired Systems and Signal Processing
290
