CLASSIFIER AGGREGATION USING LOCAL

CLASSIFICATION CONFIDENCE

David

Stefka and Martin Hole

Institute of Computer Science, Academy of Sciences of the Czech Republic

v.v.i., Pod Vod

arenskou v

ı 2, Prague, Czech Republic

Keywords:

Classiﬁer aggregation, Classiﬁer combining, Classiﬁcation conﬁdence.

Abstract:

Classiﬁer aggregation is a method for improving quality of classiﬁcation. Instead of using just one classiﬁer,

a team of classiﬁers is created, and the outputs of the individual classiﬁers are aggregated into the ﬁnal pre-

diction. In this paper, we study the potential of using measures of local classiﬁcation conﬁdence in classiﬁer

aggregation methods. We introduce four measures of local classiﬁcation conﬁdence and study their suitability

for classiﬁer aggregation. We develop two novel classiﬁer aggregation methods which utilize local classiﬁca-

tion conﬁdence and we compare them to two commonly used methods for classiﬁer aggregation. The results

on four artiﬁcial and ﬁve real-world benchmark datasets show that by incorporating local classiﬁcation conﬁ-

dence into classiﬁer aggregation methods, signiﬁcant improvement in classiﬁcation quality can be obtained.

1 INTRODUCTION

Classiﬁcation is a process of dividing patterns into

disjoint sets called classes. Many machine learn-

ing algorithms for classiﬁcation have been devel-

oped – for example naive Bayes classiﬁers, linear and

quadratic discriminant classiﬁers, k-nearest neighbor

classiﬁers, support vector machines, neural networks,

or decision trees (Duda et al., 2000).

One comonly used technique for improving

classiﬁcation quality is called classiﬁer combining

(Kuncheva, 2004) – instead of using just one classi-

ﬁer, a team of classiﬁers is created, and their results

are then combined. It can be shown that a team of

classiﬁers can perform better than any of the individ-

ual classiﬁers in the team.

There are two main approaches to classiﬁer com-

bining: classiﬁer selection (Woods et al., 1997; Ak-

sela, 2003; Zhu et al., 2004) and classiﬁer aggrega-

tion (Kittler et al., 1998; Kuncheva et al., 2001). If a

pattern is submitted for classiﬁcation, the former tech-

nique uses some rule to select one particular classiﬁer,

and only this classiﬁer is used to obtain the ﬁnal pre-

diction. The latter technique uses some aggregation

rule to aggregate the results of all the classiﬁers in the

team to get the ﬁnal prediction.

A common drawback of classiﬁer aggregation

methods is that they are global, i.e., they are not

adapted to the particular patterns that are currently

classiﬁed. However, if we use the concept of lo-

cal classiﬁcation conﬁdence (i.e., the extent to which

we can “trust” the output of the particular classiﬁer

for the currently classiﬁed pattern), the algorithm can

take into account the fact that “this classiﬁer is/is not

good for this particular pattern”.

Surprisingly, using local classiﬁcation conﬁdence

is not very common in classiﬁer combining. The goal

of this paper is to provide basic introduction to lo-

cal classiﬁcation conﬁdence measures, to study which

particular measures are suitable for classiﬁer aggrega-

tion, and to create novel classiﬁer aggregation algo-

rithms which improve the quality of classiﬁcation by

using local classiﬁcation conﬁdence.

The paper is structured as follows.After discussing

motivations in Section 2, we provide a formalism of

classiﬁer combining in Section 3. In Section 4 we

introduce four local classiﬁcation conﬁdence mea-

sures and we study their suitability with quadratic dis-

criminant classiﬁers. In Section 5, classiﬁer aggrega-

tion methods which utilize these measures are intro-

duced and their performance is tested on 9 benchmark

datasets. Section 6 then concludes the paper.

2 MOTIVATION

In the ﬁeld of classiﬁcation, several methods for

assessing the quality of classiﬁcation exist (Hand,

1997). Some of these methods try to measure the

classiﬁcation conﬁdence, i.e., the probability that the

173

Štefka D. and Hole

na M. (2009).

CLASSIFIER AGGREGATION USING LOCAL CLASSIFICATION CONFIDENCE.

In Proceedings of the International Conference on Agents and Artiﬁcial Intelligence, pages 173-178

DOI: 10.5220/0001545101730178

 SciTePress

classiﬁer predicts correctly, or the degree of trust we

can give to this classiﬁer.

Classiﬁcation conﬁdence measures can be divided

into two main groups: global measures, which assess

the classiﬁer’s predictive power as a whole (Hand,

1997; Duda et al., 2000), and local measures, which

adapt themselves to the particular pattern submitted

for classiﬁcation (Woods et al., 1997; Cheetham and

Price, 2004; Robnik-

Sikonja, 2004; Delany et al.,

2005; Tsymbal et al., 2006). Examples of global

measures can be accuracy, precision, sensitivity, re-

semblance, etc.; these have been studied intensively

since the formation of the theory of classiﬁcation. Lo-

cal classiﬁcation conﬁdence measures have not been

studied as exhaustively as global measures so far;

however, we believe they can express the classiﬁca-

tion conﬁdence better than global measures in the

context of classiﬁer combining, where local proper-

ties are more important than global ones.

Local classiﬁcation conﬁdence measures are

used for example in case-based reasoning systems

(Cheetham and Price, 2004), or in classiﬁcation tasks

where misclassiﬁcation is less acceptable than re-

fusing to classify the pattern (Delany et al., 2005).

Surprisingly, local classiﬁcation conﬁdence is used

scarcely in classiﬁer combining, where we have a

battery of different classiﬁers to use if one classi-

ﬁer refuses to classify the pattern. Even if a method

for combining classiﬁers utilizes a concept of local

classiﬁcation conﬁdence, as in (Woods et al., 1997;

Robnik-

Sikonja, 2004; Tsymbal et al., 2006), the au-

thors usually choose one particular measure of local

classiﬁcation conﬁdence, and this measure is tightly

incorporated into the combining algorithm. How-

ever, any other local classiﬁcation conﬁdence mea-

sure could be used. Moreover, creating a uniﬁed

framework for classiﬁer combining with local clas-

siﬁcation conﬁdence would be more systematic and

general approach.

In this paper, we examine the potential of incor-

porating the concept of classiﬁcation conﬁdence to

classiﬁer combining algorithms. Firstly, we propose

four local classiﬁcation conﬁdence measures and we

examine if they actually predict the probability of

correct classiﬁcation. Secondly, we develop two al-

gorithms for classiﬁer aggregation which utilize lo-

cal classiﬁcation conﬁdence and we test their perfor-

mance on three benchmark datasets.

3 CLASSIFIER COMBINING

Throughout the rest of the paper, we use the follow-

ing notation. Let X ⊆ R

be a n-dimensional fea-

ture space, an element ~x ∈ X of this space is called

a pattern, and let C

,...,C

⊆ X be disjoint sets

called classes. The goal of classiﬁcation is to de-

termine to which class a given pattern belongs. We

call a classiﬁer any mapping φ : X → [0,1]

, where

φ(~x) = (µ

,...,µ

) are degrees of classiﬁcation to

each class.

In classiﬁer combining, a team of classiﬁers

(φ

,...,φ

) is created, each of the classiﬁers predicts

independently, and then the classiﬁers’ outputs are

combined into the ﬁnal prediction. While classiﬁer

selection methods use some techniques to determine

which classiﬁer is locally better than the others, such

algorithms select only one classiﬁer, discarding much

potentially useful information, and thus reducing the

robustness compared to classiﬁer aggregation. This is

the reason why we restrict ourselves to classiﬁer ag-

gregation only in the rest of the paper.

3.1 Ensemble Methods

If a team of classiﬁers consists only of classiﬁers of

the same type, which differ only in their parameters,

dimensionality, or training sets, the team is usually

called an ensemble of classiﬁers. For this reason the

methods which create a team of classiﬁers are some-

times called ensemble methods. Well-known methods

for ensemble creation are bagging (Breiman, 1996),

boosting (Freund and Schapire, 1996), error correc-

tion codes (Kuncheva, 2004), or multiple feature sub-

set methods (Bay, 1999).

3.2 Classiﬁer Aggregation

For classiﬁer aggregation, the output of the team

(φ

,...,φ

) for input pattern ~x can be structured to a

r × N matrix, called decision proﬁle (DP):

DP(~x) =







(~x)













1,1

1,2

... µ

1,N

2,1

2,2

... µ

2,N

r,1

r,2

... µ

r,N







(1)

Many methods for aggregating the team of clas-

siﬁers into one ﬁnal classiﬁer have been proposed in

the literature. A good overview of commonly used ag-

gregation methods can be found in (Kuncheva et al.,

2001). These methods comprise simple arithmetic

rules (sum, product, maximum, minimum, average,

weighted average, etc.), fuzzy integral, Dempster-

Shafer fusion, second-level classiﬁers, decision tem-

plates, and many others.

ICAART 2009 - International Conference on Agents and Artificial Intelligence

174

4 LOCAL CLASSIFICATION

CONFIDENCE

Suppose we have a classiﬁer φ, and a pattern~x to clas-

sify. The local classiﬁcation conﬁdence of classiﬁer φ

on pattern~x is a real number in the unit interval [0,1],

and its value is obtained by a mapping κ

: X → [0, 1].

Local classiﬁcation conﬁdence can be any prop-

erty expressing our “trust” in the classiﬁer’s predic-

tion for the current pattern ~x. In the literature, many

methods for assessing local classiﬁcation conﬁdence

can be found (Woods et al., 1997; Wilson and Mar-

tinez, 1999; Avnimelech and Intrator, 1999; Delany

et al., 2005). Among them, we selected four, which

are described in the following subsections.

4.1 Local Accuracy (LA)

The local accuracy (LA) (Woods et al., 1997) mea-

sures the accuracy of a classiﬁer on a set of neighbors

of ~x. These neighbors are obtained using a k-NN al-

gorithm, i.e., the accuracy is measured on the set of

k neighbors from the validation set closest to ~x with

respect to some metric – we will denote this set as

(~x). In this paper, we use Euclidean metric. The

LA of a classiﬁer φ on ~x is computed as

(~x) =

∑

y∈NN

(~x)

(~y)

#NN

(~x)

∑

y∈NN

(~x)

(~y)

, (2)

where c

(~y) = 1 if~y is classiﬁed correctly by φ, and 0

otherwise, and #A denotes number of patterns in A.

LA is a representative of local conﬁdence mea-

sures which compute some standard global measure

of classiﬁcation quality on neighborhood of the cur-

rently classiﬁed pattern~x. Of course, any other global

measure of conﬁdence could be used.

4.2 Local Match (LM)

Delany et al., 2005, describe several methods for de-

termining local classiﬁcation conﬁdence in their spam

ﬁltering application. Most of the methods are based

on similarity of the currently classiﬁed pattern ~x to

neighboring training patterns. The main idea is that if

~x is near the decision boundary, the prediction may

not be accurate, i.e., the local classiﬁcation conﬁ-

dence should be low.

Based on the ideas behind these methods, we pro-

pose a local classiﬁcation conﬁdence measure called

local match (LM). Let NN

(~x) denote a set of k train-

ing patterns nearest to ~x (again, we used Euclidean

metric), and let NLN

(~x) denote a set of patterns from

(~x) which belong to the same class as predicted

by φ for pattern ~x. LM of φ on ~x is computed as

(~x) =

#NLN

(~x)

#NN

(~x)

#NLN

(~x)

. (3)

4.3 Conﬁdence Measures based on

Degrees of Classiﬁcation

It is also possible to use directly the output of the clas-

siﬁer, i.e., the degrees of classiﬁcation, to compute

the classiﬁcation conﬁdence. Let φ(~x) = (µ

,...,µ

and µ

(1)

, µ

(2)

be the highest and the second highest

degrees of classiﬁcation. Wilson and Martinez, 1999,

deﬁne local classiﬁcation conﬁdence as

(~x) =

(1)

∑

i=1

. (4)

We will call this measure degree of classiﬁcation ratio

(DCR). Avnimelech and Intrator, 1999, deﬁne local

classiﬁcation conﬁdence as

(~x) = (µ

(1)

− µ

(2)

)

, (5)

where s ≥ 1. We will call this measure two-best mar-

gin (TBM). These measures do not need to compute

neighboring patterns of ~x, and therefore they are very

fast compared to LA and LM.

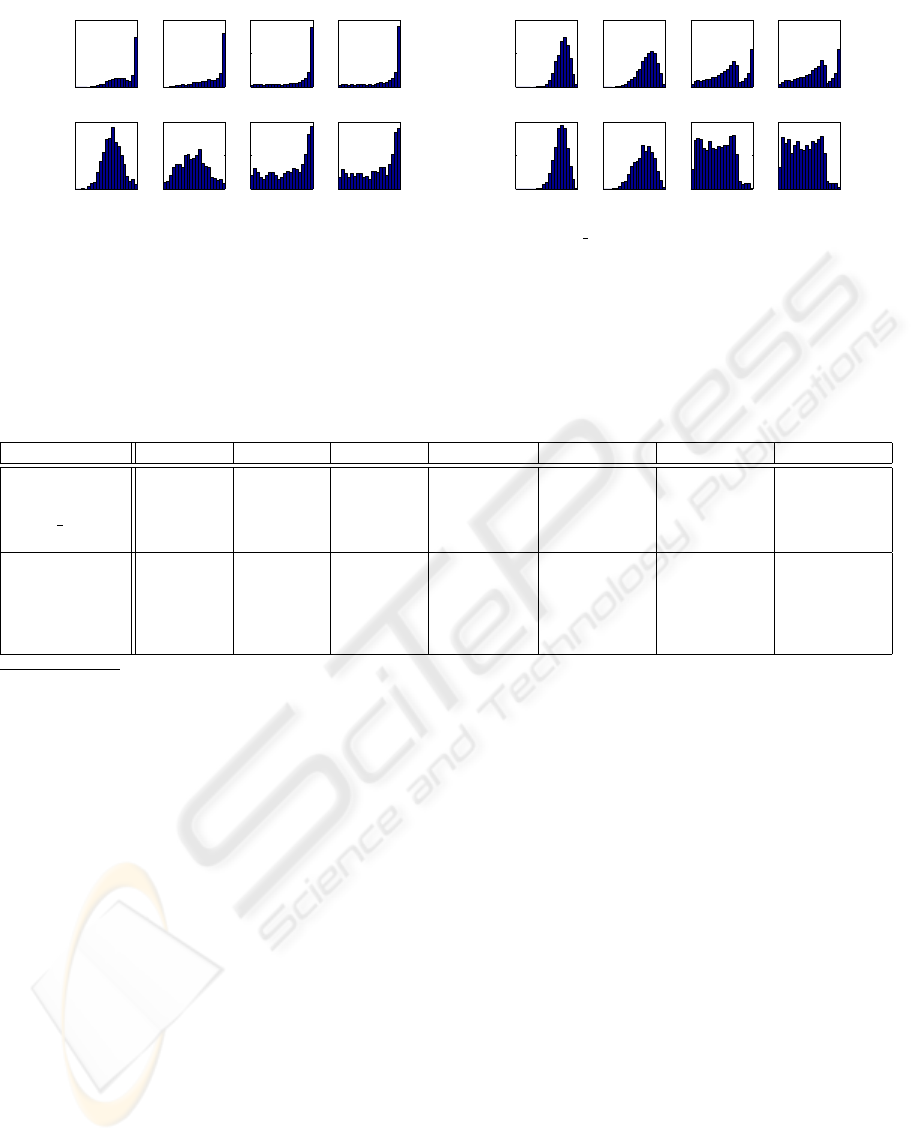
4.4 Experiment 1 - Performance of the

Proposed Measures

To get a general idea to which extent the proposed

local classiﬁcation conﬁdence measures really ex-

press the probability that the classiﬁcation of the cur-

rently classiﬁed pattern is correct, we examined the

histograms of the local classiﬁcation conﬁdence val-

ues for correctly classiﬁed (OK) and for misclassiﬁed

(NOK) patterns.

We tested the measures with a quadratic discrim-

inant classiﬁer (Duda et al., 2000) implemented in

Java programming language. 10-fold crossvalidation

was performed to obtain the results on four artiﬁcial

(Clouds, Concentric, Gauss 3D, Waveform) and ﬁve

real-world (Balance, Breast, Phoneme, Pima, Satim-

age) datasets from the Elena database (UCL MLG,

1995) and from the UCI repository (Newman et al.,

1998). The parameters of the measures were set to

k = 20 for LA and LM, and s = 1 for TBM (based

on preliminary testing; no ﬁne-tuning or optimization

was done).

Ideally, the OK distribution should be concen-

trated near one, while the NOK distribution should be

concentrated near zero, and the distributions should

be clearly separated. If the distributions overlap, or

if the NOK distribution has high values near one, it

means that the measure does not really express the

CLASSIFIER AGGREGATION USING LOCAL CLASSIFICATION CONFIDENCE

175

probability that the classiﬁcation of the currently clas-

siﬁed pattern is right.

Unfortunately, due to space constraints, we can

not show here the results for all the datasets. Gener-

ally speaking, for most of the datasets, the OK and

NOK distributions for LA and LM are quite sepa-

rated, but for DCR and TBM, the OK and NOK dis-

tributions are similar and overlapping, and the NOK

distributions have high values near one. This suggests

that the DCR and TBM measures do not really ex-

press the probability of correct classiﬁcation. Addi-

tional preliminary experiments showed that DCR and

TBM give very poor results in classiﬁer combining.

Therefore we did not further study DCR and TBM.

As for LA and LM, for most datasets, the OK and

NOK distributions are quite separated, which sug-

gests good predictive power, cf. Fig. 1(a). For some

datasets (Gauss 3D, Breast, Pima), the distributions

for LA and LM are overlapping, which suggests bad

predictive power, cf. Fig. 1(b).

5 CLASSIFIER AGGREGATION

WITH CLASSIFICATION

CONFIDENCE

In this section, we describe two commonly used al-

gorithms for classiﬁer aggregation, and two modi-

ﬁcations of these algorithms which utilize the con-

cept of local classiﬁcation conﬁdence. Recall that

(φ

,...,φ

) is a team of classiﬁers, and (1) is the out-

put of the team for a pattern ~x. Let µ

denote the ag-

gregated degree of classiﬁcation to class C

. Then we

deﬁne the following aggregation algorithms:

Mean Value Aggregation (MV) computes the ﬁnal

aggregated degree of classiﬁcation to class C

the average of all degrees of classiﬁcation to class

by all the classiﬁers φ

,...,φ

in the team:

∑

i=1

i, j

. (6)

Weighted Mean Aggregation (WM) uses weighted

mean to compute the ﬁnal prediction:

∑

i=1

i, j

∑

i=1

. (7)

The weights ω

,...,ω

are deﬁned as global con-

ﬁdences (e.g., validation accuracies) of the classi-

ﬁers in the team.

Local Weighted Mean Aggregation (LWM)

replaces the weights in the weighted mean by

local classiﬁcation conﬁdences of the classiﬁers

in the team on the currently classiﬁed pattern ~x:

∑

i=1

(~x)µ

i, j

∑

i=1

(~x)

. (8)

Filtered Mean Aggregation (FM) is a modiﬁcation

of MV, the difference being that prior to comput-

ing the mean value, classiﬁers with local classi-

ﬁcation conﬁdence on the current pattern lower

than some threshold T are discarded. If T = 0,

FM coincides with MV. If there are no classiﬁers

with local classiﬁcation conﬁdence higher than T ,

then T is lowered to the value of the maximal lo-

cal classiﬁcation conﬁdence in the team.

5.1 Experiment 2 - Performance of the

Proposed Aggregation Algorithms

In the second experiment, we tested the performance

of the classiﬁer aggregation algorithms described in

Section 5, in order to determine possible beneﬁts of

incorporating local classiﬁcation conﬁdence to classi-

ﬁer aggregation methods.

We designed an ensemble (φ

,...,φ

) of quadratic

discriminant classiﬁers (Duda et al., 2000), and we

aggregated the ensemble using the methods described

in this section (MV, WM, which do not use local clas-

siﬁcation conﬁdence, and LWM and FM using LA

and LM local classiﬁcation conﬁdence measures). We

also compared the algorithms’ performance with the

so-called non-combined classiﬁer (NC), i.e., a com-

mon quadratic discriminant classiﬁer (the NC classi-

ﬁer represents an approach which we had to use if

we could use only one classiﬁer). The 7 individual

methods will be denoted NC, MV, WM, LWM-LA,

FM-LA, LWM-LM, FM-LM. The algorithms’ perfor-

mance was tested on the same datasets as in Exp. 1.

The ensemble was created either by the bagging

algorithm (Breiman, 1996), which creates classiﬁers

trained on random samples drawn from the original

training set with replacement, or by the multiple fea-

ture subset method (Bay, 1999), which creates clas-

siﬁers using different combinations of features, de-

pending on which method was more suitable for the

particular dataset.

All the methods were implemented in Java pro-

gramming language, and 10-fold crossvalidation was

performed to obtain the results. The same parameter

values as in Exp. 1 were used, and we set T = 0.8 or

T = 0.9, depending on the particular dataset (based

on some preliminary testing; no ﬁne-tuning or opti-

mization was done).

The results of the testing are shown in Table 1.

Mean error rate and standard deviation of the error

ICAART 2009 - International Conference on Agents and Artificial Intelligence

176

0 1

1000

2000

confidence

# correctly classified

0 1

1000

2000

confidence

0 1

1000

2000

DCR

confidence

0 1

1000

2000

TBM

confidence

0 1

100

200

confidence

# misclassified

0 1

100

200

confidence

0 1

100

200

DCR

confidence

0 1

100

200

TBM

confidence

(a) Phoneme – LA, LM good separation; DCR, TBM bad

separation

0 1

500

1000

confidence

# correctly classified

0 1

500

1000

confidence

0 1

500

1000

DCR

confidence

0 1

500

1000

TBM

confidence

0 1

100

200

confidence

# misclassified

0 1

100

200

confidence

0 1

100

DCR

confidence

0 1

100

TBM

confidence

(b) Gauss 3D – all measures bad separation

Figure 1: Histograms of local classiﬁcation conﬁdence values (LA - Local Accuracy, LM - Local Match, DCR - Degree of

Classiﬁcation Ratio, TBM - Two Best Margin) for correctly classiﬁed and misclassiﬁed patterns.

Table 1: Comparison of the classiﬁer aggregation methods – non-combined classiﬁer (NC), mean value (MV), weighted mean

(WM), local weighted mean (LWM) using two conﬁdence measures (LA, LM), and ﬁltered mean (FM) using two conﬁdence

measures (LA, LM). Mean error rate (in %) ± standard deviation of error rate from 10-fold crossvalidation was calculated.

The (B/M) after dataset name means whether the ensemble was created by Bagging or Multiple feature subset algorithm.

Dataset NC MV WM LWM-LA FM-LA LWM-LM FM-LM

Clouds (M) 24.9 ± 1.4 24.9 ± 1.8 24.7 ± 1.8 23.4 ± 2.2 22.2 ± 1.7

∗†

23.1 ± 1.9 21.9 ± 1.9

∗†

Concentric (B) 3.5 ± 1.1 3.6 ± 1.1 3.4 ± 1.5 3.6 ± 1.4 1.7 ± 0.7

∗†

2.8 ± 1.4 1.6 ± 0.7

∗†

Gauss 3D (B) 21.4 ± 1.8 21.3 ± 2.2 21.4 ± 1.5 21.5 ± 2.7 21.7 ± 1.7 21.4 ± 1.6 21.6 ± 1.9

Waveform (B) 14.8 ± 1.4 14.8 ± 1.4 15.1 ± 2.0 15.0 ± 1.6 14.7 ± 0.7 14.5 ± 1.5 14.2 ± 1.9

Balance (M) 8.3 ± 3.6 11.0 ± 4.7 15.5 ± 4.2 9.0 ± 1.9 9.5 ± 3.9 8.3 ± 3.5 9.5 ± 2.5

Breast (M) 4.7 ± 3.0 4.7 ± 2.7 3.5 ± 2.6 2.9 ± 1.0 2.9 ± 1.5 3.1 ± 2.5 3.1 ± 2.6

Phoneme (M) 24.5 ± 2.0 23.7 ± 0.9 23.8 ± 2.7 21.4 ± 2.0

∗

16.8 ± 1.9

∗†

21.0 ± 1.0

∗†

16.2 ± 1.7

∗†

Pima (M) 27.0 ± 3.0 25.5 ± 6.8 26.1 ± 5.7 24.5 ± 5.0 24.2 ± 3.6 23.3 ± 4.2 25.0 ± 4.6

Satimage (B) 15.5 ± 1.6 15.5 ± 1.0 15.6 ± 1.7 15.5 ± 1.1 15.4 ± 1.0 15.1 ± 1.7 14.4 ± 1.5

∗

Signiﬁcant improvement to NC

†

Signiﬁcant improvement to MV

rate of the aggregated classiﬁers from 10-fold cross-

validation was measured. We also measured statisti-

cal signiﬁcance of the results – results which are sig-

niﬁcantly better than NC classiﬁer or MV aggrega-

tor are marked by * or † and are displayed in bold-

face. The signiﬁcance was measured at 5% level by

the analysis of variance using Tukey-Kramer method

(by the ’multcomp’ function from the Matlab statis-

tics toolbox).

The results show that for most datasets, the four

aggregation methods which use local classiﬁcation

conﬁdence (LWM-LA, FM-LA, LWM-LM, FM-LM)

outperform the two aggregation methods which do

not use local classiﬁcation conﬁdence (MV, WM). For

three datasets, these results were statistically signiﬁ-

cant. FM usually gives better results than LWM, and

if we compare the two conﬁdence measures, we can

say that LM gives usually slightly better results than

LA. Generally speaking, the FM-LM was the most

successfull algorithm in this experiment.

To summarize the results from both Exp. 1 and

Exp. 2, we can say that by incorporating local classiﬁ-

cation conﬁdence measures into classiﬁer aggregation

algorithms, signiﬁcant improvement in classiﬁcation

quality can be obtained. However, the measures of

local classiﬁcation conﬁdence sometimes do not ex-

press the probability that the classiﬁcation of the cur-

rently classiﬁed pattern is right (see Fig. 1(b)), and

therefore they do not improve classiﬁer aggregation.

The experimental results from this paper are rel-

evant to quadratic discriminant classiﬁers only, be-

cause for any other classiﬁer types (k-NN, SVM, de-

cision trees, etc.), the measures could give quite dif-

ferent results. However, it should be noted that in our

not yet published experiments with Random Forests,

we obtained similar results.

6 SUMMARY & FUTURE WORK

In this paper, we studied the concept of local classiﬁ-

cation conﬁdence and we introduced four measures of

local classiﬁcation conﬁdence. We compared the dis-

tribution of the values of the measures for correctly

CLASSIFIER AGGREGATION USING LOCAL CLASSIFICATION CONFIDENCE

177

classiﬁed and misclassiﬁed patterns for quadratic dis-

criminant classiﬁer. This experiment showed that the

DCR and TBM measures are not suitable for using

in aggregation of ensembles of quadratic discriminant

classiﬁers.

We showed a possible way how local classiﬁcation

conﬁdence can be used in classiﬁer aggregation. The

performance of these methods was compared to com-

monly used methods for classiﬁer aggregation of an

ensemble of quadratic discriminant classiﬁers on four

artiﬁcial and ﬁve real-world benchmark datasets. The

results show that incorporating local classiﬁer conﬁ-

dence into classiﬁer aggregation can bring signiﬁcant

improvements in the classiﬁcation quality.

In our future work, we plan to study local clas-

siﬁcation conﬁdence measures for other classiﬁers

than quadratic discriminant classiﬁer, mainly decision

trees and support vector machines, and to incorporate

local classiﬁcation conﬁdence into more sophisticated

classiﬁer aggregation methods.

ACKNOWLEDGEMENTS

The research presented in this paper was partially sup-

ported by the Program “Information Society” under

project 1ET100300517 (D.

Stefka) and by the Institu-

tional Research Plan AV0Z10300504 (M. Hole

na).

REFERENCES

Aksela, M. (2003). Comparison of classiﬁer selection meth-

ods for improving committee performance. In Multi-

ple Classiﬁer Systems, pages 84–93.

Avnimelech, R. and Intrator, N. (1999). Boosted mixture of

experts: An ensemble learning scheme. Neural Com-

putation, 11(2):483–497.

Bay, S. D. (1999). Nearest neighbor classiﬁcation from

multiple feature subsets. Intelligent Data Analysis,

3(3):191–209.

Breiman, L. (1996). Bagging predictors. Machine Learn-

ing, 24(2):123–140.

Cheetham, W. and Price, J. (2004). Measures of Solu-

tion Accuracy in Case-Based Reasoning Systems. In

Calero, P. A. G. and Funk, P., editors, Proceedings

of the European Conference on Case-Based Reason-

ing (ECCBR-04), pages 106–118. Springer. Madrid,

Spain.

Delany, S. J., Cunningham, P., Doyle, D., and Zamolot-

skikh, A. (2005). Generating estimates of classiﬁ-

cation conﬁdence for a case-based spam ﬁlter. In

noz-Avila, H. and Ricci, F., editors, Case-Based

Reasoning, Research and Development, 6th Interna-

tional Conference, on Case-Based Reasoning, ICCBR

2005, Chicago, USA, Proceedings, volume 3620 of

LNCS, pages 177–190. Springer.

Duda, R. O., Hart, P. E., and Stork, D. G. (2000). Pattern

Classiﬁcation (2nd Edition). Wiley-Interscience.

Freund, Y. and Schapire, R. E. (1996). Experiments with a

new boosting algorithm. In International Conference

on Machine Learning, pages 148–156.

Hand, D. J. (1997). Construction and Assessment of Clas-

siﬁcation Rules. Wiley.

Kittler, J., Hatef, M., Duin, R. P. W., and Matas, J. (1998).

On combining classiﬁers. IEEE Trans. Pattern Anal.

Mach. Intell., 20(3):226–239.

Kuncheva, L. I. (2004). Combining Pattern Classiﬁers:

Methods and Algorithms. Wiley-Interscience.

Kuncheva, L. I., Bezdek, J. C., and Duin, R. P. W.

(2001). Decision templates for multiple classiﬁer fu-

sion: an experimental comparison. Pattern Recogni-

tion, 34(2):299–314.

Newman, D., Hettich, S., Blake, C., and Merz, C.

(1998). UCI repository of machine learning databases.

http://www.ics.uci.edu/∼mlearn/MLRepository.html.

Robnik-

Sikonja, M. (2004). Improving random forests.

In Boulicaut, J., Esposito, F., Giannotti, F., and Pe-

dreschi, D., editors, ECML, volume 3201 of Lecture

Notes in Computer Science, pages 359–370. Springer.

Tsymbal, A., Pechenizkiy, M., and Cunningham, P.

(2006). Dynamic integration with random forests. In

Frnkranz, J., Scheffer, T., and Spiliopoulou, M., edi-

tors, ECML, volume 4212 of Lecture Notes in Com-

puter Science, pages 801–808. Springer.

UCL MLG (1995). Elena database.

http://www.dice.ucl.ac.be/mlg/?page=Elena.

Wilson, D. R. and Martinez, T. R. (1999). Combining

cross-validation and conﬁdence to measure ﬁtness. In

Proceedings of the International Joint Conference on

Neural Networks (IJCNN’99), paper 163.

Woods, K., W. Philip Kegelmeyer, J., and Bowyer, K.

(1997). Combination of multiple classiﬁers using lo-

cal accuracy estimates. IEEE Trans. Pattern Anal.

Mach. Intell., 19(4):405–410.

Zhu, X., Wu, X., and Yang, Y. (2004). Dynamic classiﬁer

selection for effective mining from noisy data streams.

In ICDM ’04: Proceedings of the Fourth IEEE In-

ternational Conference on Data Mining (ICDM’04),

pages 305–312, Washington, DC, USA. IEEE Com-

puter Society.

ICAART 2009 - International Conference on Agents and Artificial Intelligence

178