
UNIFIED ICA-SPM ANALYSIS OF FMRI EXPERIMENTS
Implementation of an ICA Graphical User Interface for the SPM Pipeline
Troels Bjerre†, Jonas Henriksen†, Carsten Haagen Nielsen†, Peter Mondrup Rasmussen††
Lars Kai Hansen†† and Kristoffer Hougaard Madsen‡
†DTU Electrical Engineering, Technical University of Denmark, Ørsteds Plads Building 348, 2800 Kgs. Lyngby, Denmark
††DTU Informatics, Technical University of Denmark, Richard Petersens Plads Building 321, 2800 Kgs. Lyngby, Denmark
‡DRCMR, Copenhagen University Hospital Hvidovre, Kettegaard All´e 3, 2650 Hvidovre, Denmark
Keywords:
Bayesian Information Criterion (BIC), Functional Magnetic Resonance Imaging (fMRI), General linear model
(GLM),
ica4spm
, Independent Component Analysis (ICA), Statistical Parameter Mapping (SPM).
Abstract:
We present a toolbox for exploratory analysis of functional magnetic resonance imaging (fMRI) data using
independent component analysis (ICA) within the widely used SPM analysis pipeline. The toolbox enables
dimensional reduction using principal component analysis, ICA using several different ICA algorithms, se-
lection of the number of components using the Bayesian information criterion (BIC), visualization of ICA
components, and extraction of components for subsequent analysis using the standard general linear model.
We demonstrate how the toolbox is capable of identifying activity and nuisance effects in fMRI data from a
visual experiment.
1 INTRODUCTION
Statistical parametric mapping (SPM) is the domi-
nant tool for analysis of functional brain data acquired
from medical imaging modalities such as positron
emission tomography (PET) and functional magnetic
resonance imaging (fMRI) (Frackowiak et al., 2003),
and is aimed at identification of functionally special-
ized brain regions. SPM is a voxel based hypothesis
driven method that examines regionally specific re-
sponses on the basis of standard inferential statistics.
The typical functional imaging experiment in-
volves a group of subjects undergoing a common
set of stimuli the stimuli time course is referred to
as the ‘paradigm’. Among hypothesis-driven meth-
ods the far most common model employed is the
general linear model (GLM), where the response
in each voxel is modeled as a linear combination
of a number of explanatory variables, typically de-
rived from the paradigm, and a noise term. Since
each voxel is treated individually this approach is
commonly referred to as a mass-univariate approach.
In fMRI changes in the blood oxygen level depen-
1
The first four authors are listed alphabetically. They
contributed equally to this work.
dent (BOLD) signal can be modeled by incorporation
of information regarding the experimental paradigm,
physiological- (e.g., cardiac and respiratory effects)
and non-physiological artifacts (e.g. head move-
ment and hardware instabilities) into the design ma-
trix (Frackowiak et al., 2003; Lund et al., 2006).
Data-driven methods are less committed, explorative,
and aim to discover the underlying structure of the
data rather than impose given a priori knowledge on
the model. Principal component analysis (PCA) and
independent component analysis (ICA) are multivari-
ate methods that take interactions between voxels into
account, and hereby characterize brain responses as
spatial-temporal patterns (McKeown et al., 2003a).
ICA allows for discovery of components that are sta-
tistically independent, where each component is char-
acterized by a spatial map and a time course. The
technique has proven to be useful in extraction of
independent components (ICs) related to the exper-
imental design, physiological and non-physiological
noise as well as being capable of identification of
brain activations that have been difficult to specify
beforehand, for a review, see e.g., (McKeown et al.,
2003a).
This paper concerns a software tool for the com-
bination of hypothesis- and a data-driven strategies.
316
Bjerre T., Henriksen J., Haagen Nielsen C., Rasmussen P., Hansen L. and Hougaard Madsen K. (2009).
UNIFIED ICA-SPM ANALYSIS OF FMRI EXPERIMENTS - Implementation of an ICA Graphical User Interface for the SPM Pipeline.
In Proceedings of the International Conference on Bio-inspired Systems and Signal Processing, pages 316-321
DOI: 10.5220/0001547803160321
Copyright
c
SciTePress

Figure 1: Left; The SPM data analysis pipeline. First step (1) is preprocessing, second step (2) is model design and parameter
estimation and third step (3) is the statistical inference. The
ica4spm
toolbox is aimed as a intermediate step between the
first and second step. Right; Flow chart for the
ica4spm
toolbox. Signal processing includes dimensionality reduction via
PCA, ICA decomposition and BIC model order estimation. The final volumes contain images of the different components
activation magnitude.
Based on ICA decomposition of the image set, both
‘neural response’ or ‘noise’ components are deter-
mined and hereafter incorporated as explanatory vari-
ables in the model specification in a conventional
SPM analysis. This unified methodology is not novel
and has earlier been proposed by e.g., (Hu et al.,
2005). In their approach, univariate SPM is combined
with multivariate ICA, where inference of statistical
significance of ICs obtained from an ICA analysis
is conducted within the mass-univariate SPM frame-
work.
While there are excellent tools available for fMRI
analysis that parallels the present toolbox, such as
the Group ICA of fMRI Toolbox (GIFT) by Calhoun
et al. (http://icatb.sourceforge.net), the toolbox pre-
sented here is the first to fully integrate ICA (and
PCA) linear multivariate methods into SPM.
We thus present a MATLAB R2007b (The Math-
Works, Natick, Massachusetts, USA) implementation
of a unified methodology comprising of the follow-
ing steps: I) Dimension reduction with PCA. II) ICA
decomposition, with model order selection by the
Bayesian information criterion (BIC) (Hansen et al.,
2001a). III) Visualization of spatial map, time course
and frequency content of ICs. IV) Export of rel-
evant ICs for easy inclusion in specification of the
GLM in a conventional SPM analysis. The tool-
box and a user manual can be downloaded from
http://isp.imm.dtu.dk/toolbox/ica/
.
Our design goals for the
ica4spm
toolbox were
to develop a toolbox that is easy and intuitive for the
neuroscience researcher to use and compatible with
the SPM5 software package (Wellcome Department
of Imaging Neuroscience, University College Lon-
don). The toolbox is intended as an intermediate step
in the conventional SPM pipeline outlined in Fig. 1.
Our toolbox facilitates identification and extraction of
ICs related to noise or the paradigm. Relevant ICs
can conveniently be exported and included in the de-
sign matrix specification in SPM. Hereby our tool-
box is not a ‘direct competitor’ to the GIFT toolbox,
which has many additional functions and statistical
tests, but rather an intuitive tool for researchers fa-
miliar with the SPM software package and the statis-
tical inference framework in SPM. The presentation is
organized as follow. First, we briefly review the the-
ory behind multivariate methods such as PCA, ICA
and model selection based on BIC. Secondly, we give
some general considerations about the combined ap-
proach. Finally, we present our implementation and
an example of an analysis of an fMRI data set.
2 THEORY
Let the response variable in a given voxel be defined
by the random variable Y
i
, where i ∈ [1 : N] are the
observations. The GLM General Linear Model ex-
presses the response variable as a linear combination
of L explanatory variables, where L < N plus an error
term (Frackowiak et al., 2003)
Y
i
= x
i1
β
1
+ x
i2
β
2
+ ... + x
iL
β
L
+ ε
i
, (1)
where β
l
are unknown parameters. It is assumed,
that the errors ε
i
are independent and identically dis-
tributed (i.i.d.) normal random variables with zero
mean and variance σ
2
, that is ε
i
∼ N (0, σ
2
). In ma-
trix notation the GLM is written as Y = Xβ+ε, where
X ∈ R
N×L
is the design matrix and β ∈ R
L×1
is the
parameter vector. The design matrix contains the
explanatory variables. These variables could be di-
rectly related to the paradigm or related to confoun-
UNIFIED ICA-SPM ANALYSIS OF FMRI EXPERIMENTS - Implementation of an ICA Graphical User Interface for the
SPM Pipeline
317

ding effects. Model parameters are determined by
least square estimation.
2.1 Principal Components Analysis
Principal Components Analysis (PCA) is a multivari-
ate statistical method for analysis or dimension re-
duction of multidimensional data sets. It is based on
an orthogonal linear transformation of the data into
a new coordinate system, where the data is projected
in the directions with the most variance defined by
the eigenvectors corresponding to the largest eigen-
values of the covariance matrix, see e.g., (Hansen
et al., 1999). A basic tool for PCA is singular value
decomposition (SVD) of the data matrix, see e.g.,
(Smith, 2002). An fMRI data set describes a tempo-
ral development of the acquisition volume, thus forms
a 4D data structure of dimensions X ∈ R
L×M×N×T
,
where L, M, and N are the physical dimensions of
a single recorded volume at a given time, while T
is the time dimension. Before performing PCA and
ICA, this data set is reshaped into two dimensions
X ∈ R
P×T
, where P = L × M × N denotes the num-
ber of voxels. The SVD of the matrix X ∈ R
P×T
is
given as X = USV
T
, where U ∈ R
P×T
and V ∈ R
T×T
are orthogonal matrices with the sorted eigenvectors
of
1
T
XX
T
and
1
P
X
T
X respectively (McKeown et al.,
1998). S ∈ R
T×T
is a diagonal matrix with the sorted
singular values, which are the standard deviation val-
ues in the different directions. The dimensions of U, S
and V described here, are those obtained by perform-
ing the so-called thin PCA decomposition where only
the first T instead of P columns of U and T instead
of P rows of S are calculated. When the variance of
the noise is small, the dimensionality reduction from
X ∈ R
P×T
to X ∈ R
K×T
is performed by linear trans-
formation to the sub-space spanned by the K eigen-
vectors of U corresponding to the K largest eigenval-
ues of S, i.e.,
˜
X =
˜
U
T
X. After the PCA transforma-
tion, dimensionality reduction is carried out by retain-
ing the lowest order principal components, hence, the
dimensions of the data set that contribute most to its
variance.
2.2 Independent Component Analysis
The nature of the BOLD fMRI signal suggests that
blind source separation (BSS) techniques are rele-
vant for reconstructing individual signal components
(McKeown et al., 1998). In BSS, source signals are
recovered from mixtures without knowing the mixing
coefficients. The source signals can be related to, e.g.,
stimulus response, the heartbeat, respiratory related
confounds, and motion artifacts. ICA is a method
for solving the BSS problem, where multivariate sig-
nals are separated into components or sources that
are statistically independent (McKeown et al., 1998;
Hyv¨arinen and Oja, 2000). In general, the ICA de-
composition can be written as:
X = AS X
n,t
=
K
∑
k=1
A
n,k
S
k,t
, (2)
where X
n,t
is the signal at the n’th voxel and K is the
number of independent components. In matrix nota-
tion A ∈ R
K×K
is the mixing matrix and S ∈ R
K×N
is
the source matrix. In (2), the sources as well as the
mixing coefficients are unknown, hence, the mixing
matrix can be determined up to scaling and permuta-
tion (Hyv¨arinen and Oja, 2000).
ICA can be used to separate either spatially or
temporally independent sources (McKeown et al.,
2003b; Hu et al., 2005). In temporal ICA (tICA), a
single independent component is a set of voxels in A
that are activated by an independent time function in
S. In spatial ICA (sICA) the time courses in S of each
voxel are derived in such a way, that the columns in A
are statistically independent.
Numerous approaches exist for solving the ICA
problem. The toolbox
ica4spm
offers the following
algorithms:
• Maximum Likelihood (also known as Infomax)
(Bell and Sejnowski, 1995; Hansen et al., 2001b)
• Molgedey-Schuster (Molgedey and Schuster,
1994; Hansen et al., 2001b; Kolenda et al., 2001)
• Joint approximate diagonalization of eigenmatri-
ces (JADE) (Cardoso, 1999)
• Fast Fixed-Point Algorithm for Independent
Component Analysis (FastICA) (Hyv¨arinen and
Oja, 1997)
These algorithms have all been evaluated in fMRI
contexts, see e.g., (Correa et al., 2007).
2.3 Probabilistic Model Selection
The conditional probability P(m|X) of a specific
model hypothesis m = 0,..,T given the observed data
X can be calculated using Bayes’ theorem,
P(m|X) =
P(X|m)P(m)
∑
m
P(X|m)P(m)
, (3)
where P(m) is the prior probability of the specific
model given by P(m) = 1/(T + 1) if there is no prior
knowledge. P(X|m) is the conditional probability of
the measured data using the hypothesis of the spe-
cific model. In (Kolenda et al., 2001; Højen-Sørensen
et al., 2002; Hu et al., 2005) BIC Bayes Information
BIOSIGNALS 2009 - International Conference on Bio-inspired Systems and Signal Processing
318

Criterion was proposed for model order selection in
order to select the number of independent component
in fMRI data sets. Let θ be the parameters that de-
scribe a specific ICA model. Then the optimal model
is found by maximizing the BIC approximation to (3),
BIC = log(P(X | θ
MAP
,m) −
1
2
W log(N), where m is
a specific model, θ
MAP
are the maximum likelihood
parameters, W is the number of parameters and N is
the number of data points. In
ica4spm
we offer model
order estimation for the Maximum Likelihood and the
Molgedey-Schuster algorithms.
3 MATERIALS AND METHODS
The fMRI data set used in the demonstration of the
ica4spm
toolbox was collected from a single subject
with a 3T scanner (Magnetom Trio, Siemens, Erlan-
gen Germany) using a gradient echo EPI sequence.
The following settings were used: Echo time TE =
30 ms, repetition time TR = 2.37 s, in-plane resolu-
tion 3 × 3 mm, flip angle α = 90
◦
, slice thickness 3
mm, and interleaved acquisition without gaps. The
subject was visually stimulated during the scan using
an 8 Hz reversing checkerboard with an expanding
ring, where each period lasted 30 s. The activation is
therefore expected to be present in the occipital cor-
tex at a frequency of 1/30 Hz with phase depending
on the position in the visual cortices. Rigid-body re-
alignment of the data was done using SPM2 (Well-
come Department of Imaging Neuroscience, Univer-
sity College London) to minimize movement artifacts
and the data was spatially smoothed with a Gaussian
kernel in order to suppress high frequency noise. An
overview of the signal processing is shown in Fig. 1.
We performed two ICAs on the demonstration data
set, one on the entire dataset (381 volumes) selected
ICs from this analysis is displayed in Fig. 3. In the
second analysis we aim to show how ICA can be used
to identify signal components to be used in a subse-
quent analysis. In order to be able to test for activation
in the subsequent analysis unbiased we divide the data
set into a training set and a test set. Relevant ICs were
identified with the toolbox in the training set and in-
cluded in a subsequent SPM analysis of the test data
set (using SPM5). The statistical inference was done
using an F-test with voxelsactivations considered sig-
nificant for p-values < 0.001. Results from this ana-
lysis is displayed in Fig. 3. In both cases we used a
temporal MS ICA with automatically selected τ and
a number of components based on BIC. The
ica4spm
toolbox is designed and tested in MATLAB R2007b
as a GUI add-on to the SPM software package. The
front end is set up by the script
ica4spm
. The objects
in the user interface have different callbacks enabling
different functions depending on the task required. If
possible, SPM5 functionalities have been used in the
toolbox interface to ease the use for potential users al-
ready familiar with SPM5. Three global variables are
used. These are: a structure containing all handles to
the GUI-figure and its controls, a structure containing
all input variables and calculated parameters by the
PCA, ICA and BIC, and finally a structure with the
handles and variables containing parameters for the
SPM-visualization.
4 RESULTS
The user interface consist of two windows, the main
window
ica4spm
and the component visualization
window
ICA visualization
displayed in Fig. 2.
The main window gives the user the ability to setup
an appropriate ICA. The initial step of the ICA will
be to reduce the dimensionality with PCA. The tool-
box gives the user the option to automatically select
the dimensionality based on the optimal numbers of
principal components calculated by BIC, or use the
BIC as a guidance when specifying the dimension for
the data set entering ICA.
In order to support large data sets and reduce the
computationalworkload it is possible to mask the data
to only include relevant parts of the images. Masking
can be performed based on the mean value or variance
of the voxels in the images across time. The data is
thresholded so either a fraction of voxels with highest
mean values or a fraction with greatest variance is in-
cluded in the analysis. The toolbox enables the user
to manually review the masks before the actual pro-
cessing. Masks obtained from other sources such as
SPM5 can also be loaded and used.
The toolbox offers the possibility of selecting ei-
ther temporal or spatial ICA, currently four ICA al-
gorithms are implemented in the toolbox: Maximum
Likelihood (ML), Molgedey Schuster (MS), JADE,
and FastICA. For the MS algorithm the user has the
ability to manually define a desirable value of τ. As
default the MS algorithm estimates an optimal value.
When the user has selected the desired analysis, ICA
will be performed automatically by pressing Start
Analysis. After processing the results will be dis-
played in the component visualization window.
The visualization window enables the user to in-
vestigate the individual ICs superimposed on a co-
registered anatomical volume. The superimposed
components are shown in the transverse, coronal, and
sagittal planes. The user has the ability to threshold
the visualization of a component, so only a percentage
UNIFIED ICA-SPM ANALYSIS OF FMRI EXPERIMENTS - Implementation of an ICA Graphical User Interface for the
SPM Pipeline
319

Figure 2: Left; The main user interface for the
ica4spm
toolbox. Right; Example of the ICA visualization user interface of
the
ica4spm
toolbox showing a temporal MS ICA component.
of the greatest/least intense voxels are superimposed.
In addition, it is possible to examine the temporal pat-
tern and frequency content of each IC and compare
that to a paradigm. If the user finds it relevant to in-
clude a given IC in the GLM, the toolbox facilitates
specification and export of the IC for use in a sub-
sequent SPM analysis. Fig. 3 shows three selected
components from a temporal MS ICA performed on
the demonstration data set. The temporal profile and
frequencycontents of the two first componentsclearly
indicate that these components are related to the vi-
sual paradigm with a 30 second period and the spatial
map show activity restricted to the visual areas of the
brain. The analysis has split visual activity into two
components allowing it to capture activity regardless
of the phase. The last component shows how the ICA
has also captured nuisance signal variation related to
the cardiac cycle. Notice, that the temporal profile of
this component appears aliased due the low sampling
rate. Figure 3 shows a test for significant effects in the
test data set based on paradigm related ICs identified
in the training data set.
5 DISCUSSION & CONCLUSION
Our
ica4spm
toolbox facilitates easy unsupervised
exploratory analysis and visualization of relevant sig-
nal components from a data set and the use of ex-
tracted ICs in a SPM analysis. From the
ica4spm
main GUI, it is easy to load fMRI data and select
which settings to use for the ICA. If selected, PCA is
performed for dimensionality reduction of the data set
and BIC can be used to automatically for determin-
ing the number of relevant signal components. This
makes it easy to ensure that all relevant signal com-
ponents are discovered. The components of interest
can be saved to a design matrix and loaded in SPM5.
Generally, the use of structures in the program have
made it possible to access all data and variables at all
times.
ICA was found useful when applied to a real fMRI
data set, as it was able to identify both paradigm and
nuisance related effects. The activation related to the
paradigm was split into two components with differ-
ent phases in order to model any phase of the visual
stimuli. In subsequent SPM analysis with the time
series as regressors in the design matrix, we found
strong visual cortex as expected, see Fig. 3. Our
findings are equivalent to those found in (Lund et al.,
2006) for the same data set. Furthermore, it was pos-
sible to recognize ICs containing the pulse and res-
piration, making it possible to include these as con-
founding effects in the design matrix. In conclusion,
we found that the GUI may prove useful in the analy-
sis of fMRI data.
ACKNOWLEDGEMENTS
This work is supported by the Lundbeck Foundation
through the Center for Integrated Molecular Brain
Imaging (www.cimbi.dk).
BIOSIGNALS 2009 - International Conference on Bio-inspired Systems and Signal Processing
320
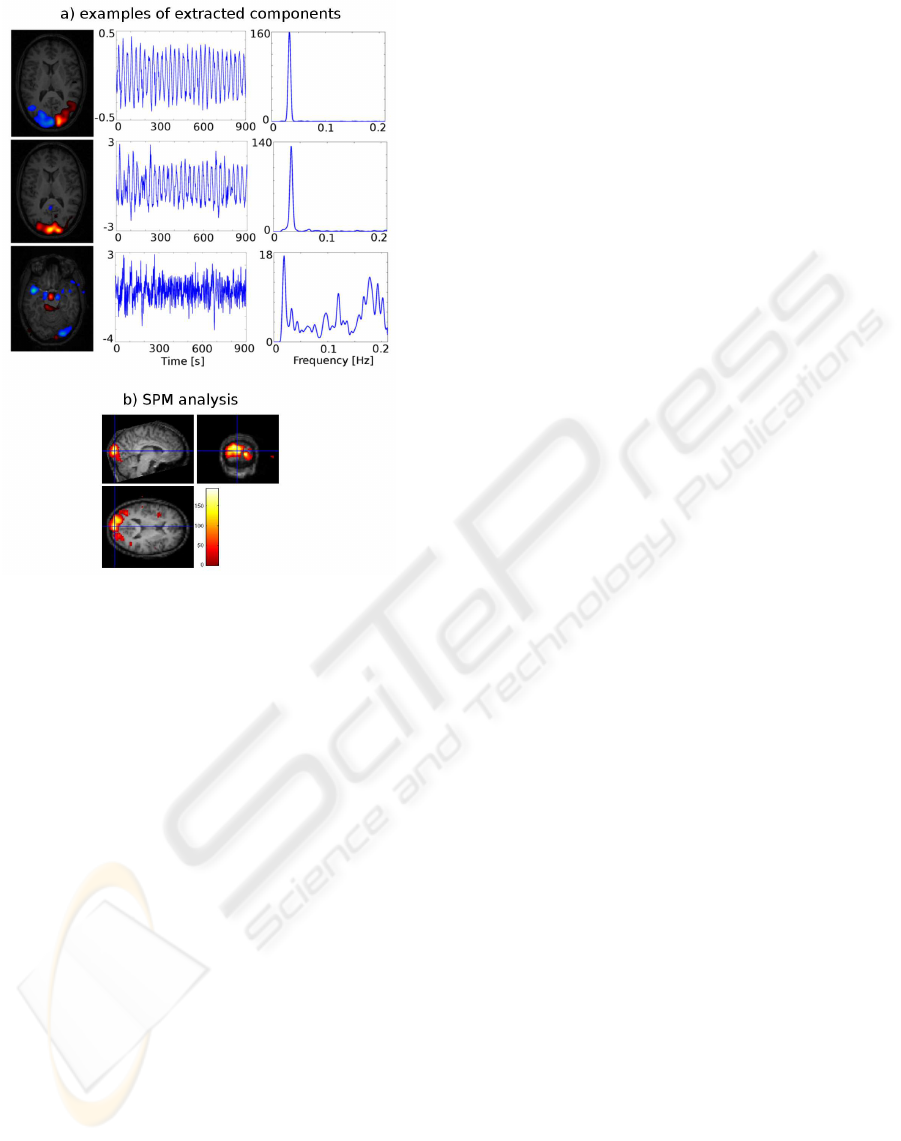
Figure 3: Top; Three selected components from ICA per-
formed on the demonstration dataset. To the left the spatial
map from each component is showed as an overlay on the
anatomical scan. For the first two components a slice near
the calcarine sulcus is shown whereas a slice near the cir-
cle of Willis is shown for the last component. The middle
column of figures shows the temporal profile for each of the
components and the right column shows the power spec-
trum (Welch method). The first two components are clearly
related to the visual paradigm with prominent activity in the
occipital cortex whereas the last component is related to car-
diac nuisance effects. Buttom; F-test conducted in SPM5
on test data set for significant effects of paradigm related
ICs identified in the training data set. Thresholded at p <
0.001 uncorrected.
REFERENCES
Bell, A. and Sejnowski, T. (1995). An information-
maximization approach to blind separation and blind
deconvolution. Neural Computation, 7:1129–1159.
Cardoso, J.-F. (1999). High-order contrasts for independent
component analysis. Neural Comput., 11(1):157–192.
Correa, N., Adali, T., and Calhoun, V. (2007). Performance
of blind source separation algorithms for fmri analy-
sis using a group ica method. Magnetic Resonance
Imaging, 25(5):684–694.
Frackowiak, R., Friston, K., Frith, C., Dolan, R., Price, C.,
Zeki, S., Ashburner, J., and Penny, W. (2003). Human
Brain Function. Academic Press, 2nd edition.
Hansen, L., Larsen, J., and Kolenda, T. (2001a). Blind de-
tection of independent dynamic components. Acous-
tics, Speech, and Signal Processing, 2001. Proceed-
ings. (ICASSP ’01). 2001 IEEE International Confer-
ence on, 5:3197–3200.
Hansen, L., Larsen, J., and Kolenda, T. (2001b). Blind de-
tection of independent dynamic components. Acous-
tics, Speech, and Signal Processing, 2001. Proceed-
ings.(ICASSP’01). 2001 IEEE International Confer-
ence on, 5.
Hansen, L., Larsen, J., Nielsen, F., Strother, S., Rostrup, E.,
Savoy, R., Lange, N., Sidtis, J., Svarer, C., and Paul-
son, O. (1999). Generalizable Patterns in Neuroimag-
ing: How Many Principal Components? Neuroimage,
9(5):534–544.
Højen-Sørensen, P., Winther, O., and Hansen, L. (2002).
Analysis of functional neuroimages using ICA adap-
tive binary sources. Neurocomputing, 49(1):213–225.
Hu, D., Yan, L., Liu, Y., Zhou, Z., Friston, K. J., Tan, C.,
and Wu, D. (2005). Unified spm-ica for fmri analysis.
NeuroImage, 25:746–755.
Hyv¨arinen, A. and Oja, E. (1997). A fast fixed-point al-
gorithm for independent component analysis. Neural
Computation, 9(7):1483–1492.
Hyv¨arinen, A. and Oja, E. (2000). Independent component
analysis: Algorithms and applications. Neural Net-
works, 13(4-5):411–430.
Kolenda, T., Hansen, L., and Larsen, J. (2001). Signal
detection using ICA: Application to chat room topic
spotting. Third International Conference on Indepen-
dent Component Analysis and Blind Source Separa-
tion, pages 540–545.
Lund, T., Madsen, K., Sidaros, K., Luo, W., and Nichols,
T. (2006). Non-white noise in fMRI: Does modelling
have an impact? Neuroimage, 29(1):54–66.
McKeown, M., Hansen, L., and Sejnowsk, T. (2003a). Inde-
pendent component analysis of functional MRI: what
is signal and what is noise? Current Opinion in Neu-
robiology, 13(5):620–629.
McKeown, M., Hansen, L., and Sejnowsk, T. (2003b). Inde-
pendent component analysis of functional mri: what is
signal and what is noise? Current Opinion in Neuro-
biology, 13(5):620–629.
McKeown, M., Makeig, S., Brown, G., Jung, T., Kinder-
mann, S., Bell, A., and Sejnowski, T. (1998). Analysis
of fmri data by blind separation into independent spa-
tial components. Human Brain Mapping, 6(5):160–
188.
Molgedey, L. and Schuster, H. (1994). Separation of
independent signals using time-delayed correlations.
Physical Review Letters, 72(23):3634–3637.
Smith, L. (2002). A tutorial on Principal Components Ana-
lysis. Cornell University, USA, 51:52.
UNIFIED ICA-SPM ANALYSIS OF FMRI EXPERIMENTS - Implementation of an ICA Graphical User Interface for the
SPM Pipeline
321
