AN EFFICIENT AND ROBUST TECHNIQUE OF T WAVE

DELINEATION IN ELECTROCARDIOGRAM

Yogendra Narain Singh

Department of Computer Science & Engineering, Institute of Engineering & Technology, Lucknow, India

P. Gupta

Department of Computer Science & Engineering, Indian Institute of Technology Kanpur, Kanpur, India

Keywords:

ECG analysis, T wave delineation, QRS complex.

Abstract:

This study presented an efﬁcient and robust method for the automatic delineation of T wave in the single-lead

electrocardiogram. The method attained optimum performance using the fusion of delineation results obtained

from a pair of new approaches. The ﬁrst approach utilizes the advantage of time derivative and determines T

wave ends using derivative curve analysis. The effect of local noise on the ECG signal is seized using a non-

derivative approach which performs T wave delineation using the analysis of its waveform curvature toward

the ends. Using the assumption that beginning and end of T wave exhibit the convex shape, this approach

determines minimum radius of curvature of the convex regions at both ends. It is formally shown that the time

instance corresponding to minimum radius of curvature coincides with T wave ends. The delineation results

obtained from both the approaches are fused to achieve the optimum performance. The delineator attained a

detection sensitivity of 99.9%, positive predictivity of 99.1% and an accuracy of 99.01% over the ﬁrst lead

of physionet QT database (20 records of 1, 000 beats each). The delineation errors are found well within the

referenced intercardiologist observations, especially for T wave end. The mean error and standard deviation

are found smaller than 10 ms which outperformed in comparison to other published results.

1 INTRODUCTION

The Electrocardiogram (ECG) is the record of time-

varying bio-electric potential generated by the electri-

cal activity of the heart. ECG provides an easiest way

to monitor the functional activity of the heart without

using of an invasive method. It is a prima tool used

by the cardiologists in diagnosis of cardiac arrhyth-

mia. In the automatic analysis of ECG, locating the

beginning (onset) and end (offset)ﬁducials of its char-

acteristic waveforms, the most difﬁcult one among

these measurements is the delineation of T wave. T

wave is the representation of repolarization of ven-

tricles whereby the myocardium is prepared for the

next cycle of ECG. In the automatic delineation of T

wave, the detection of its offset ﬁducial is more cum-

bersome due to rapid change of the signal near to its

end. Furthermore, the end of T wave also concerns

the irregularity causing in the electrical activity of the

heart. The patterns of cardiac impulses responsible

for T wave generation has been identiﬁed using the

different methods available in the literature.

The information of time derivative has been uti-

lized for the automatic detection of T wave end ﬁdu-

cials in the multilead ECG signals (Laguna et al.,

1994). A similar method based on wavelet trans-

form has taken the advantage of numerical differen-

tiation and its robustness to the waveform variations

(Li et al., 1995). The disadvantage of this method is

its sensitivity towards the noise. In order to limit the

noise-sensitivity, smoothing ﬁlters are used. Among

the other methods of T wave delineation, one of them

has consisted to the computation of an indicator re-

lated to the area covered by T wave curve (Zhang

et al., 2005). It is constituted with its consistency

proof based on assumptions, essentially on the con-

cavity of T wave. The offset ﬁducial is detected on

the basis of the fact that maximum of the computed

indicator inside each cardiac cycle coincides with T

wave end.

Mathematical models of ECG have also been ap-

plied to waveform detection. Morphological model of

146

Narain Singh Y. and Gupta P. (2009).

AN EFFICIENT AND ROBUST TECHNIQUE OF T WAVE DELINEATION IN ELECTROCARDIOGRAM.

In Proceedings of the International Conference on Bio-inspired Systems and Signal Processing, pages 146-154

DOI: 10.5220/0001548401460154

 SciTePress

one P-QRS-T complex is formulated using a set of or-

dinary differential equations. It is ﬁtted to ECG signal

segments by tuning the model parameters, and then

used to locate the waveform boundaries (McSharry

et al., 2005). These methods are in principal noise-

insensitive and easily adapted to the change in ECG

morphology, but they are highly computationally ex-

pensive and also suffered to parameter overheads.

While investigation of T wave delineation meth-

ods, it is found that each method has own strength(s)

and weakness(es). In this paper, a novel method of T

wave delineation is proposed. It is consisted of a pair

of new approaches that resulted an efﬁcient and robust

way to delineate T wave in ECG. Both approaches are

used lowpass ﬁlter for ECG signal correction from

baseline oscillations. For an infallible detection of

T wave and its end ﬁducials, a search window is set

heuristically based on the length of a typical QT in-

terval. Adaptive thresholding technique is utilized to

detect the true presence of T wave in each heartbeat.

The determination of onset (T

onset

) and offset (T

of f set

)

ﬁducials of T wave is resulted using the approach of

(1) derivative curve analysis and (2) waveform cur-

vature analysis. The resulted ﬁducials obtained from

both the approaches are fused to delineate the ﬁnal T

wave ends.

The reminder of this paper is organized as follows.

In Section 2 the schematic description of automated

T wave delineation is presented. A high level de-

scription of the method used for heartbeat detection is

also summarized in this section. A novel method of T

wave delineation, consisting a pair of new approaches

namely, derivative curve analysis and waveform cur-

vature analysis is given in Section 3. In order to eval-

uate the performance of the proposed method, the re-

sults of validation and its signiﬁcance are presented

in Section 4. A comparison of results with other pub-

lished methods are also given in this section. Finally,

conclusions are drawn in Section 5.

2 SYSTEM DESCRIPTION

The automated delineation of T wave concerns ECG

signal analysis and diagnostic method. The correction

of the signal from non-signal artifacts including digi-

tization and sampling is the concern of signal analy-

sis. The schematic diagram of the automated T wave

delineation system is shown in Figure 1. The task of T

wave delineation carries out in following stages: The

preprocessing stage consists of signal acquisition and

heartbeat detection. The ECG data is acquired from

the individuals and subsequently it is digitized. The

digitized signal is passed to the heartbeat detection

Figure 1: Schematic description of automatic T wave delin-

eation.

module. The heartbeat detection module utilizes QRS

complex delineator algorithm which is implemented

using the method of Pan and Tompkins with some

improvements (Pan and Tompkins, 1985). The algo-

rithm can be divided into ﬁltering and decision rules.

The aim of ﬁltering of the signal is to generate a win-

dowed (or time limited) estimate of the energy in the

QRS frequency band. It is achieved by applying the

following tasks: (1) lowpass ﬁlter of cutoff frequency

16Hz and delay of nearly 20ms, (2) highpass ﬁlter of

cutoff frequency 8Hz and delay of nearly 60ms, (3)

derivative unit that extracts slope information of de-

lay nearly 5ms, (4) absolute value function that causes

QRS detector to be less gain-sensitive while Pan and

Tompkins have used squaring function that caused

nonlinear ampliﬁcation, and (5) moving window in-

tegrator that captures QRS complexes in ECG. The

average size of moving window is set to 80ms wide

while in the original algorithm window has been set

to 150ms wide that allowed the wider QRS complexes

produced by the Premature Ventricular Contractions

(PVC) and the merging of QRS complexwith T wave.

After ﬁltering, the signal is free from noise and noise

artifacts. The signal is then ready for the delineation

of QRS complexes. The decision rules are used that

make a distinction between QRS event and the noise

event. The rules are framed from the physiology of

the normal QRS complex in the ECG while the de-

tection of QRS peak are carried out using adaptive

thresholding technique.

In order to determine the windowed region for the

existence of a normal T wave, the end ﬁducial of QRS

complex (QRS

of f set

) is to be delineated. The ﬁdu-

cial QRS

of f set

is delineated according to the location

and the convexity of R peak. The search region for

QRS

of f set

is set according to the width of QRS com-

plex relative to FP (R peak). Within the region, the

signal is traced in time-forward order and search the

sample where slope is lesser than quarter of minimum

slope. In order to insure that found QRS

of f set

position

is not an inﬂection some adjustment surrounding to

the detected position need to be performed.

The computed QRS

of f set

ﬁducial is then passed to

AN EFFICIENT AND ROBUST TECHNIQUE OF T WAVE DELINEATION IN ELECTROCARDIOGRAM

147

Amplitude (mV)

Time (ms)

80ms

QRS

offset

80ms

QRS

offset

470ms

Figure 2: Setting of the search window for T wave delin-

eation.

the processing stage at T wave delineator. The delin-

eator uses this ﬁducial as a reference for the setting

of search window where the proposed delineation ap-

proaches are implemented.

3 T WAVE DELINEATION

The delineation is concerned to the detection of char-

acteristic waveform and its limits. The processing

steps utilize for T wave delineation includes lowpass

ﬁltering, setting of a search window and the threshold

estimation. For the reliable delineation of T wave, os-

cillatory patterns of the isoelectric potential must be

minimized. It can be achieved by ﬁltering of the ECG

signal through a second order recursive lowpass ﬁlter

(Lynn, 1977) of following time difference equation,

= 2∗ y

(n−1)T

−y

(n−2)T

−2∗x

(n−4)T

(n−8)T

(1)

where x

represents the data sample of size n at dis-

crete instant of time T. At sampling frequency of 100

Hz, T is found to be 10 ms and processing delay

caused by the ﬁlter is nearly 30 ms.

Prior to start of the delineation process, a tem-

poral window (search window) is deﬁned that deter-

mines a probable region of the existence of T wave in

each heartbeat. The boundaries of the search window

are set heuristically relative to QRS

of f set

ﬁducial as

shown in Figure 2. The search window that approx-

imately contains the T

onset

and T

of f set

ﬁducials is ex-

tended from QRS

of f set

+ 80ms to QRS

of f set

+ 470ms

positions in each heartbeat. It can also observed that

the segment of 80ms from QRS

of f set

ﬁducial is ex-

cluded from the search window because this is the

time prior to repolarization of ventricles that have the

negligible stimulation. Similarly, the right boundary

of the search window is set according to the duration

of depolarization to repolarization of the ventricles.

In order to discuss the main features of the pro-

posed T wave delineator the morphology of the wave-

form is considered as positive as shown in Figure 2.

The other morphologies of T wave can be treated sim-

ilarly.

3.1 T Wave Detection

The procedure for detection of T wave from each beat

of the ECG signal is as follows: First of all, peak

of the entitled signal which is the signal within the

search window is determined using the time deriva-

tive approach. Using adaptive thresholdingtechnique,

one can classify that detected peak is a true peak or a

non peak of T wave. The threshold is calculated us-

ing the estimates of peak heights and the level of high

frequency noise present in the beat. The threshold (ϑ)

is set between the mean of peak height (µ

peak

) and the

mean of high frequency noise (µ

noise

) according to

the formula,

ϑ = C

∗



peak

− µ

noise



(2)

where the threshold coefﬁcient (C

) lies between 0

and 1. This experiment is conducted on C

= 0.23.

The mean of peak height is estimated from the height

of ﬁve recently detected peaks. The mean of high fre-

quency noise is estimated from the level of high fre-

quency noise (HF

noise

) present in the detected peak

using the following approach: The beat is ﬁrstly

passed to a highpass ﬁlter of following time differ-

ence equation,

= x

− 2∗ x

(n−1)T

+ x

(n−2)T

(3)

The level of artifact signals can be estimated by

taking the mean of y values of ﬁve consecutive sam-

ples. Then maximum of the means is computed for

the entire beat. Let it be denoted as HF

noise

. Finally, a

noise metric is obtained using the ratio of HF

noise

and

R wave peak height (h

peak

) according to the formula,

noise

∗







peak



(4)

where the parameters (C

, C

) can be determined and

set through the experiment. These values are set as

= 50 and C

= 4 during the experiment.

3.2 End Fiducials Detection

The beginning of T wave is concerned to the start

of ventricles repolarization which is raising (dropping

BIOSIGNALS 2009 - International Conference on Bio-inspired Systems and Signal Processing

148

for negative T wave) slowly while the end of T wave

is concerned to the end of repolarization cycle which

is terminating much faster. The changes resulted from

abnormal function of epicardium and/or endocardium

can also be seen in the latter part of T wave. Along to

that, it is also noticed that its end segment shows a rel-

atively lower stimulation in comparison to the level of

noise present in the beat. That makes the detection of

end ﬁducials of T wave, especially T

of f set

more cum-

bersome. Keeping the concern of these observations,

the end ﬁducials of T waves, T

onset

and T

of f set

are to

be determined efﬁciently and more robustly using the

following proposed approaches.

Both approaches utilize a linear derivative ﬁlter

which corrects ECG signal from isoelectric oscilla-

tions. The ﬁrst approach takes the advantage of time

derivative to capture the signal variations. Further-

more, it determines T

onset

and T

of f set

ﬁducials through

derivative curve analysis which is obtained from the

ﬁltered signal. The approach produces better delin-

eation results when the end positions of T wave are

relatively free from local noise. For the cases, when

the end positions of T wave are contaminated highly

with local noise then it yields less accurate results.

This is due to the sensitiveness of time derivative

to the local noise. The pitfall of the ﬁrst approach

can be overcame in the non-derivative based second

approach. The implementation bases of second ap-

proach is the assumption that the curvature of T wave

near to its ends is convex. It extracts the T wave

end ﬁducials using the analysis of the curvature to-

ward both ends. The accuracy of the delineated re-

sults of this approach is highly depends on the as-

sumption that the end ﬁducials of T wave are found at

the sample corresponding to minimum radius of cur-

vature of its waveform at both ends. These results are

reported more robust to the local noise than most ob-

vious derivative measure.

3.2.1 Derivative Curve Analysis

This approach utilizes the advantage of time deriva-

tive to capture the signal variations. The derivative

approximation can be implemented using the follow-

ing difference equation,

= x

− x

(n−1)T

(5)

where the delay of the derivative ﬁlter is set to nearly

10ms at sampling frequency of 100Hz. A snapshot of

the ﬁltered signal and the signal after implementing

derivative approximation is shown in Figure 3. For

determining T wave end ﬁducials, process starts with

ﬁnding the peak of derivative signal within the search

window. The peak is determined at the location where

maximum change in the slope is occurred. Let this

Amplitude (mV)

Time (ms)

peak

max

Raw Signal Filtered Derivative

Figure 3: Detection of T wave end ﬁducials using derivative

curve analysis within the search window.

location be denoted as d

peak

. The procedure to de-

termine the T

of f set

ﬁducial is as follows: Once d

peak

is known, derivative signal is traced from d

peak

to d

positions in time-forward order. The d

position can

be set at the right most boundary of the search win-

dow i.e., QRS

of f set

+ 470ms. Let a line L

is drawn

extending from d

peak

position to d

position where

the coordinates of these positions are (x

peak

) and

) respectively. Thus, the equation of L

can be

formulated as,

≡ y− y

peak

= Slope ∗



x− x

peak



(6)

where Slope can be computed by,

Slope =

− y

peak

− x

peak

(7)

Along with the entitled signal, vertical offset of each

sample in [d

peak

, d

] to the line L

is computed. Let d

be some position in [d

peak

, d

] in the derivative signal

whose coordinate be (x

). The vertical offset (δ

)

corresponds to d

, can be computed using the follow-

ing formula,

=| y

peak



− y

peak





− x

peak



∗



− x

peak



− y

| (8)

Maximum among δ

’s is selected. The desired posi-

tion at which the vertical offset of the entitled signal is

maximum, is the position of T

of f set

. The found sam-

ple at position d

where vertical offset is maximum

e.g., δ

max

= Max(δ

) is the T

of f set

ﬁducial as shown

in Figure 3.

A similar approach is used for the detection of

onset

ﬁducial within the search window. The deriva-

tive signal is traced from d

peak

to d

position in time

reverse order where the position d

is set at leftmost

boundary of the search window, i.e. QRS

of f set

+80ms

as shown in Figure 3. In the derivative signal, a line

is drawn extending from d

peak

to d

position. Let

AN EFFICIENT AND ROBUST TECHNIQUE OF T WAVE DELINEATION IN ELECTROCARDIOGRAM

149

the coordinate of d

be (x

). Along to the deriva-

tive signal, vertical offset δ

is computed for each po-

sition d

(where d

∈ [d

peak

]) to the line L

in time

reverse order according to the formula,

=| y

peak



− y

peak





− x

peak



∗



− x

peak



− y

| (9)

where (x

, y

) is the coordinate corresponding to posi-

tion d

. Among all d

’s, a position is found where the

value of the vertical offset (δ

) of the entitled signal is

maximum, i.e., δ

max

= Max(δ

). The found position

returns the T

onset

ﬁducial as shown in Figure 3.

3.2.2 Waveform Curvature Analysis

It is a non derivative based approach which is capable

to limits the noise sensitivity of the cardiac signal and

determines T wave end ﬁducials using the analysis of

waveform curvature found at its ends.

Notations and Heuristics Basis. It is assumed that

the origin of a T wave which a stage prior to ventric-

ular repolarization and the end of T wave which is a

stage prior to the end of ventricular stimulation, ex-

hibit convex shapes at ends. It means, two convex

regions can be considered at the neighborhood of T

wave ends. The boundaries of both convex regions

are extended towards peak of the waveform so that it

becomes the common extremity of both regions. Let

and t

are two time instances corresponding to the

beginning and the end of T wave as shown in Fig-

ure 4. Consequently, the aim is to determine the time

instances t

and t

as waveform end ﬁducials whose

neighboring regions are convex. Let these regions are

separated by the peak position, t

peak

. The proposed

approach determines T wave end ﬁducials, T

onset

and

of f set

through tracking down the entitled signal and

ﬁnding the sample of minimum radius of curvature at

both convex regions which is found to be more robust

to local noise.

This approach starts its processing with the ﬁl-

tered signal which is corrected from signal oscilla-

tions around isoelectric line. A search window is set

heuristically and an interval [t

] is delimited inside

the search window in each beat of the ECG. The inter-

val is delimited with an observation that the time po-

sitions t

and t

which correspond to T wave ends are

completely inside the interval and the time positions

and t

are on opposite side of t

peak

. The peak posi-

tion can be determined by ﬁnding of local maximum,

while the extremities of the interval, t

and t

can be

determined by ﬁnding of local minimum at both sides

of t

peak

in the entitled signal within the search win-

dow.

Amplitude (mV)

Time (ms)

max

peak

-∆t

max

peak

+∆t

peak

Figure 4: Detection of T wave end ﬁducials using waveform

curvature analysis within the search window.

Assumption 1. The segments of T wave within the

intervals [t

peak

] and [t

peak

] are convex.

Typically, T wave is convex in the neighborhoods

of time instances t

and t

while it shows concaveness

in interval [t

]. It is acknowledged from the mor-

phology of T waveform that the onset of T wave (i.e.,

) and the time instant t

which limits this onset of the

waveform are laid on isoelectric line. The deﬂection

of T wave shows the time evolution of electrical activ-

ity caused by ventricular repolarization which starts

after the electrical activity caused by delayed depo-

larization of ventricles. It shows a signiﬁcant time

gap (∼ 80ms in normal objects) between the start of

ventricular repolarization and the late ventricular de-

polarization where cardiac impulse neutralizes each

other and resulting approximately zero difference in

electrical potential. This time gap is referred as iso-

electric period. In this considerationit is also assumed

that the interval [t

] is strictly inside the isoelectric

period.

Similarly, the offset of T wave (i.e., t

) and the

time instant t

which limits the onset of the wave-

form are laid on isoelectric line. During the interval

], cardiac muscles are prepared for next cycle of

the heartbeat. The preparation time of myocardium

prior to the start of next cycle of the heartbeat is sub-

stantially larger, while the impulse deﬂections during

this period are insigniﬁcant. Thus, this period can be

considered as isoelectric period. Similarly, it is also

assumed that the interval [t

] is strictly inside the

isoelectric period.

Proposition 1. Under assumption 1 and the ﬁxing of

time differences between following intervals:

1. (t

peak

− △t, t

) and (t

peak

− △t, t

peak

− τ

); where

∈ [t

peak

− △t,t

];

2. (t

peak

+ △t, t

) and (t

peak

+ △t, t

peak

+ τ

); where

∈ [t

peak

+ △t,t

] and △t ≥ 0.

BIOSIGNALS 2009 - International Conference on Bio-inspired Systems and Signal Processing

150

the time instances t

and t

can be determined as the

position of minimum radius of curvature between time

differences 1 and 2, respectively.

Proof: For case 1 the waveform is traced from t

peak

position in time reverse order. Assume that

U and

V are directed line segments drawn between the time

difference (t

peak

− △t, t

) and (t

peak

− △t, t

peak

− τ

)

respectively as shown in Figure 4. Here, point of in-

terest is the time instance t

which is the position of

minimum radius of curvature of the waveform seg-

ment in interval [t

peak

]. The radius of curvature is

computed using the principal of vector cross product

between two directed line segments

U and

V. Let δ

be the perpendicular offset of two directed line seg-

ments

U and

V as shown in Figure 4 then δ

can be

determined using following formula,

V | sinθ (10)

where,

sinθ =

1−





U |

V |

(11)

Let the deﬁnition of line segments in time amplitude

system be given as

U =





and

V =





then δ

can be computed using Eqn. (10) and (11) as

follows,

−

(12)

In general, the perpendicular offset δ

can be deter-

mined using Eqn. (12) at any time instance τ

, where

∈ [t

peak

− △t,t

Once the perpendicular offsets (for ∀τ

) are

known, the position of time instance corresponding

to minimum radius of curvature can be determined by

ﬁnding of the sample where δ

is maximum. Let it be

max

, i.e.,

max

= Max

peak

−△t

,. . . , δ

(13)

It returns the position to the time instance t

Similarly, for case 2 one can determine the di-

rected line segments

U and

V between the time dif-

ference (t

peak

+ △t, t

) and (t

peak

+ △t, t

peak

+ τ

respectively. The perpendicular-offset δ

between the

directed line segments can be determined by tracking

the segment of signal from t

peak

position to t

position

in time forward order for all τ

, where τ

is in [t

peak

△t,t

] as shown in Figure 4. Finally, the time instance

corresponding to minimum radius of curvature of the

segment in the interval [t

peak

] can be determined

by δ

max

, where δ

max

= Max

peak

+△t

,. . . , δ

It returns the position to the time instance t

The proposed approach extracts T wave end ﬁdu-

cials in two stages. In the ﬁrst stage, peak posi-

tion is determined by ﬁnding of local maximum in

the region surrounding to T wave whose boundaries

are limited through the search window in each heart-

beat. In the second stage, T

onset

and T

of f set

ﬁducials

are determined by tracking downhill the ﬁltered sig-

nal and ﬁnd the location of minimum radius of curva-

ture at both ends. Experimental result shows that the

detected ﬁducials are more robust to high frequency

noise in the beat.

3.3 Fusion of Delineation Performance

In this work, T wave delineator takes the advantage

of both the proposed approaches. It is found that the

approach based on the analysis of waveform curva-

ture returns more accurate T wave end ﬁducials when

the assumption 1 is satisﬁed. That is the region sur-

rounded to onset and offset positions of T wave is

convex. Otherwise, the approach based on the anal-

ysis of derivative curve produces better result. Thus,

for a reliable and accurate detection of T wave end

ﬁducials, the delineation results obtained from both

the approaches are fused. In this work, the fusion of

delineated results is obtained by taking mean of both

the results.

3.4 Other T Wave Morphologies

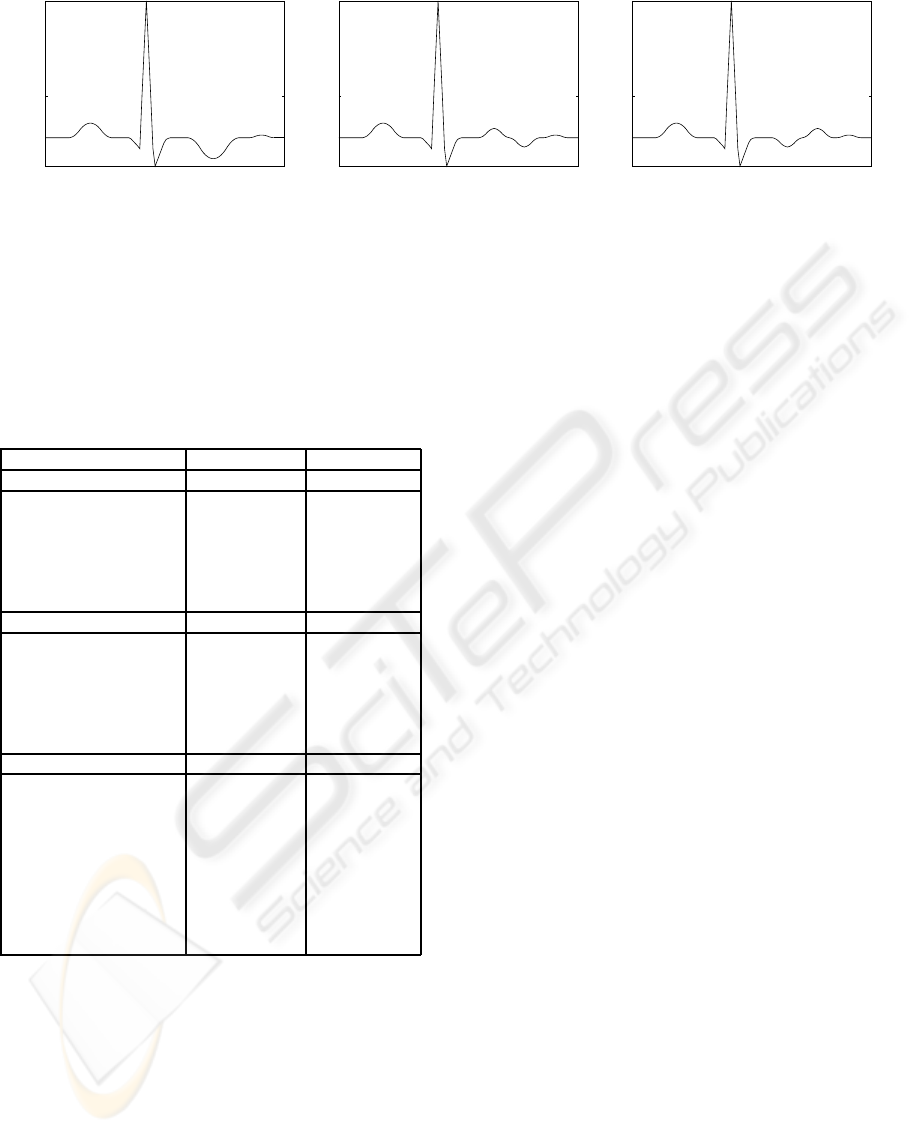
T wave morphologies can be generally classiﬁed as

positive, negative, and biphasic as shown in Figure

5. The delineation approaches proposed here are for-

mulated for the positive T waves of the ECG. The

other T wave morphologies can be treated as follows:

For negative T wave the proposed approaches perform

equally well. The only difference ﬁnds in this case

is the detection of time instance to the peak of the

entitled signal which is associated to the local min-

imum instead of local maximum in both approaches.

In biphasic case, local maximum-minimum can be de-

termined for biphasic positive-negative T wave and

minimum-maximum can be determined for biphasic

negative-positive T wave. The end ﬁducials of bipha-

sic (positive-negative) T wave can be determined by

tracking of the entitled signal downhill from maxi-

mum position in time-reverse order for the detection

of T

onset

and uphill from the minimum position in

time-forward order for the detection of T

of f set

in both

approaches. The end ﬁducials of biphasic (negative-

positive) T wave can be determined vice-versa.

AN EFFICIENT AND ROBUST TECHNIQUE OF T WAVE DELINEATION IN ELECTROCARDIOGRAM

151

Voltage (mV)

Time (ms)

Voltage (mV)

Time (ms)

Voltage (mV)

Time (ms)

Figure 5: Examples of different morphologies of T wave, (a) Negative, (b) Biphasic positive-negative and (c) Biphasic

negative-positive.

Table 1: Detection performance of T wave in QT

database. Se measures the waveform detection sensi-

tivity (Se(%) = 100 × TP/(TP+ FN)). The estimate

of the detection of true waveform is determined by P

(%) = 100 × TP/(TP+ FP)). Acc determines the

measurement of delineation accuracy (Acc(%) = 100 ×

(TP+ TN)/(TP+ TN +FP+ FN).

Technique Parameters T wave

# annotations 3542

TP N/R

FP N/R

WT Detector FN N/R

(Martinez et al., 2004) Se (%) 99.77

(%) 97.79

Acc(%) N/R

# annotations 2500

TP N/R

FP N/R

MD Detector FN N/R

(Sun et al., 2005) Se (%) 99.6

(%) N/R

Acc (%) N/R

# annotations 20000

TP 19980

(999@1000)

FP 180

(9@1000)

Proposed Work FN 20

(1@1000)

Se (%) 99.9

(%) 99.1

Acc (%) 99.01

The approaches utilize for T wave delineation typ-

ically determine the morphology of its waveform a

priori to its onset and offset detection. A simple ap-

proach that distinguishes biphasic T wave with its

other waveforms (e.g., positive T wave or negative T

wave) can be the searching of zero crossing in the sig-

nal within the search window. If there is an existence

of zero-crossing then T wave is biphasic; otherwise it

is either a positive T wave or a negative T wave.

4 EXPERIMENTAL RESULTS

The performance of the proposed T wave delineator

is evaluated on Physionet QT database (Laguna et al.,

1997) which served as a reference for the validation

and the comparisons of T wave delineation methods.

The performance of T wave detection and the deter-

mination of its end ﬁducials are validated on manually

annotated samples of this database.

QT database is a mixed database contains 105

ﬁfteen minutes excerpts of two-channel ambulatory

ECG recordings. The recordings are digitized at

250 Hz per channel with 11-bit resolution over a

10 mV range. It contains following databases, 15

from MIT-BIH Arrhythmia database, 6 from MIT-

BIH ST Change database, 13 from MIT-BIH Supra-

ventricular Arrhythmia database, 10 from MIT-BIH

Normal Sinus Rhythm database, 33 from European

ST-T database, 24 from Sudden Death from MIT-BIH

database and 4 records from MIT-BIH Long Term

ECG database. In this work the MIT-BIH Arrhyth-

mia database and MIT-BIH Normal Sinus Rhythm

database, ﬁrst channel recordings have been used for

analysis.

In this experiment, the performance of T wave de-

tection is measured on following terminologies: TP is

the true detection of T waves. FN returns the waves

those are not registered in the automatic delineation

process. FP returns those waves that are detected in-

correctly. In order to quantify the accuracy of the pro-

posed delineator mean error (µ

) and standard devi-

ation (σ

) of the differences between the annotation

results and the automated delineator results are also

computed. The mean error is used to measure the

closeness between them while σ

measures stability

in the delineation results. Sensitivity (Se), positive

predictivity (P

) and accuracy (Acc) are also com-

puted to measure the detection performance.

BIOSIGNALS 2009 - International Conference on Bio-inspired Systems and Signal Processing

152

Table 2: End Fiducials detection performance of T wave and its comparison with different methods in QT database. (N/R:

Not Reported)

Technique Parameters T

onset

of f set

# annotations 3542 3542

± σ

(ms) N/R -1.6 ±18.1

WT Detector Se (%) 99.77 99.77

(Martinez et al., 2004) P

(%) 97.79 97.79

Acc (%) N/R N/R

# annotations 2500 2500

± σ

(ms) 7.9±15.8 8.3 ±12.4

MD Detector Se (%) 99.8 99.6

(Sun et al., 2005) P

(%) N/R N/R

Acc (%) N/R N/R

# annotations 20000 20000

± σ

(ms) 0.9±7.8 5.3±9.7

Proposed Work Se (%) 99.9 99.8

(%) 99.1 99

Acc (%) 99.01 98.8

Tolerance Limit

(The CSE Working Party, 1985) σ

(ms) ... 30.6

4.1 Waveform Detection

The performance of the proposed delineator for T

wave detection on Physionet QT database is shown in

Table 1. In this study, ﬁrst 8 seconds of the selected

record is used for training purpose and setting of the

parameters. Therefore this portion of the sample is

exempted from validation. From rest of the sample,

1000 peak annotations are selected. The experiment

is conducted on 20 records and the results are shown

in Table 1 which are compared with the results ob-

tained from some of the well known methods, WT

detector (Martinez et al., 2004) and MD detector (Sun

et al., 2005). Among the 1000 peak annotations of T

waves, the proposed delineator is detected 999 waves

correctly and 9 waves incorrectly while it is left only

one wave from the detection, on an average from one

record. It is achieved the detection Se of 99.9% and

of 99.1% which is higher than any of the pub-

lished results. The accuracy of T wave detection is

measured and found more than 99 % which is not re-

ported (N/R) in the other methods.

4.2 End Fiducials Detection

The statistical results for µ

, σ

, Se, P

and Acc of

onset

and T

of f set

ﬁducials obtained from the proposed

delineator are shown in Table 2 and are compared

with other published results. The accepted σ

toler-

ance from the measurements recommended by CSE

(The CSE Working Party, 1985) is also given in the

last row of the this Table.

The delineator takes the advantages of the pro-

posed approaches and achieves outstanding delin-

eation performance on the evaluated database. Lower

values of mean error and standard deviation for T

onset

ﬁducial are observed in comparison to MD detector

while these values are not reported in WT detector.

The mean error for T

of f set

ﬁducial obtained in this

work (5.3 ms) is found better than MD detector (8.3

ms) while WT detector performed best (-1.6 ms). The

standard deviation for T

of f set

ﬁducial is reported bet-

ter than any of the published results and found well

within the acceptable limit recommended by the CSE

working party. This signiﬁes the robustness in the

detection of the end ﬁducial of T waveform. Never-

theless, the end ﬁducial is delineated much efﬁciently

with the Se = 99.8%, P

= 99% and an accuracy of

98.8%. The mean error and standard deviation for

onset

ﬁducial are also found better than both WT and

MD detectors. These results of T wave delineation are

better than any of the published methods.

5 CONCLUSIONS

This paper has presented a novel method of T wave

delineation which showed an efﬁcient detection of T

wave and its end ﬁducials in the single-lead electro-

cardiogram. The performance of the proposed sys-

tem has validated on standard annotated database on

a total of 20000 (20x1000) peak annotations. The re-

sults have shown a reliable and accurate delineation of

AN EFFICIENT AND ROBUST TECHNIQUE OF T WAVE DELINEATION IN ELECTROCARDIOGRAM

153

T wave which outperformed in comparison to other

published results on the referenced database. The

method has detected T waves and their end bound-

aries with an accuracy of more than 99% annotated

by cardiologists in the ECG.

The delineation errors in this experiment have

found well within the referenced inter-cardiologist

observations, especially for the detection of T wave

end. The remarkable performance of T wave delin-

eation has been achieved, due to the utilization of

different approaches of basis the time derivative and

other than the time derivative. The mean error and

standard deviation of T wave end ﬁducials have been

found smaller than one inter sample time which is 10

ms.

REFERENCES

Laguna, P., Jane, R., and Caminal, P. (1994). Automatic

detection of wave boundaries in multilead ECG sig-

nals: Validation with the CSE database. Computers

and Biomedical Research, 27(1):45–60.

Laguna, P., Mark, R. G., Goldberger, A. L., and Moody,

G. B. (1997). A database for evaluation of algorithms

for measurement of QT and other waveform intervals

in the ECG. Computers in Cardiology, pages 673–

676.

Li, C., Zheng, C., and Tai, C. (1995). Detection of ECG

characteristic points using wavelet transforms. IEEE

Transaction on Biomedical Engineering, 42(1):21–28.

Lynn, P. A. (1977). Online digital ﬁlters for biological sig-

nals: some fast design for a samll computer. Medical

& Biological Engineering & Computing, 15.

Martinez, J. P., Almeida, R., Olmos, S., Rocha, A. P., and

Laguna, P. (2004). A wavelet-based ECG delineator:

Evaluation on standard database. IEEE Transactions

on Biomedical Engineering, 51(4):570–581.

McSharry, P. E., Clifford, G. D., Tarassenko, L., and Smith,

L. A. (2005). A dynamic model for generating syn-

thetic electrocardiogram signals. IEEE Transactions

on Biomedical Engineering, 50(3):289–294.

Pan, J. and Tompkins, W. J. (1985). A real time QRS de-

tection algorithm. IEEE Transactions on Biomedical

Engineering, 32(3):230–236.

Sun, Y., Chan, K. L., and Krishnan, S. M. (2005). Charac-

teristic wave detection in ECG signal using morpho-

logical transform. BMC Cardiovascular Disorders,

28:1417–2261.

The CSE Working Party (1985). Recommendations for

Measurement Standards in Quantitative Electrocar-

diography. European Heart Journal.

Zhang, Q., Manriquez, A. I., and Medigue, C. (2005). An

algorithm for robust and efﬁcient location of t-wave

ends in electrocardiogram. Computers in Cardiology,

33.

BIOSIGNALS 2009 - International Conference on Bio-inspired Systems and Signal Processing

154