A SIMPLE METHOD OF CORTICAL BONE THICKNESS

EVALUATION BASED ON RADIOGRAPHIC IMAGES FOR

OSTEOPOROSIS INVESTIGATION

Przemysław Maćkowiak, Ryszard Stasiński

Department of Electronics and Telecommunications,Poznań University of Technology, Polanka 3, Poznań, Poland

Tomasz Kulczyk

Department of Biomaterials and Experimental Dentistry, Poznań University of Medical Sciences, Poland

Keywords: Osteoporosis population screening, Dental panoramic radiographs, Automatic bone borders extraction.

Abstract: In the paper a method of automatic extraction of cortical bone based on dental panoramic radiographs is

described. The method is intended for use as the first contact tool in osteoporosis population screening. Its

components have very low computational complexity, and can be found in every image processing software

package. The upper and lower boundaries of mandibular cortical bone have been determined in a series of

panoramic images, and results have been evaluated by a radiologist. The technique works either very

precisely, or clearly wrong (for heavily cluttered images), which proves its usefulness for an untrained user.

1 INTRODUCTION

Osteoporosis is a disease primarily affecting older

people, especially women aged over 60, and which

may lead to wrist, hip and vertebra fractures

(Torsoni et al., 2006). The modern gold standard for

evaluating osteoporosis is a BMD (Bone Mineral

Density) examination of the lumbar spine or/and

femoral neck. Currently access to a BMD

examination is limited as it is not possible to carry

out screening of all women over 65.

An alternative population screening test may be

based on the evaluation of certain parameters of

dental panoramic radiographs (Horner et al., 2002).

Dental panoramic images show the facial parts of

the skull with the upper and lower jaw and some

neighbouring structures. A particularly interesting

structure visible in a panoramic image is the cortical

bone of the lower border of mandible in the vicinity

of the mental foramen (Figure 1). Its parameters, e.g.

the width of the cortical bone and distance from the

lower border of the mandible to the mental foramen

can be measured as well as some characteristic

morphological features of the bone. If CW is below

3mm, an individual should be referred for the further

osteoporosis investigation (Horner et al., 2002).

Figure 1: Portion of a dental panoramic radiograph

showing the cortical bone and the mental foramen.

Analysis of morphological structures, in

conjunction with the results of measurements such

as PMI (Panoramic Mandibular Index), have been

correlated with data from a BMD test to investigate

any relationship between them. Some authors

believe that analysis of a panoramic image can result

in a dentist advising his patient to have a BMD test,

"because from your dental panoramic image it looks

as though you are in danger of osteoporosis” (Devlin

et al., 2007). The advantages of such a “screening

test“ are both economic and safe, since the

270

ckowiak P., Stasi

nski R. and Kulczyk T. (2009).

A SIMPLE METHOD OF CORTICAL BONE THICKNESS EVALUATION BASED ON RADIOGRAPHIC IMAGES FOR OSTEOPOROSIS INVESTIGA-

TION.

In Proceedings of the International Conference on Health Informatics, pages 270-275

DOI: 10.5220/0001549102700275

 SciTePress

panoramic image has already been taken for other

purposes and the patient is not subject to additional

radiation. Such a test should be automated, as

evaluations done by general dental practitioners may

differ importantly from those given by radiologists

(Devlin et al., 2001).

Currently it exists only few works on automatic

analysis of panoramic images for osteoporosis

examination, and the based on active contours

(snakes) method from paper (Devlin et al., 2007)

requires specialised software. This article presents a

computer algorithm consisting of simple and

readibly available components, which seems to

provide reliable measurements of the cortical bone.

The article is divided as follows. Chapter two

describes the research material. Third chapter is the

algorithm description. The fourth and the fifth

chapter are the discussion and the results. The last

ones are the conclusions and the literature.

Figure 2: The region of interests for the right and left sides

of a panoramic radiograph at the mandible.

2 RESEARCH MATERIAL

40 digital dental panoramic images have been taken

using the CRANEX TOME dental panoramic unit

and a DIGORA PCT PSP DIGITAL SCANNER.

Images of 3258x1764 resolution have been provided

by the Section of Dental Radiology in the

Department of Biomaterials and Experimental

Dentistry, Poznań University of Medical Sciences.

Two small parts of the image from the left and right

sides were cut off by the radiologist to create regions

of interest (ROI) for further analysis. Each ROI has

had a rectangular shape and has contained the region

extending from edge of mental foramen down to and

below the lower edge of cortical bone, as illustrated

in Figure 2. The size of the ROI may vary but must

include the region around the mental foramen and

extend below the lower border of mandible.

3 ALGORITHM DESCRIPTION

The goal is to determine the upper and lower

boundaries of the cortical bone accurately. This task

requires generation of two images, A and B,

specified in sections 3.1 and 3.2. The images are

inputs to a contour extraction method described in

section 3.3, leading to determination of the desired

boundaries. The algorithm is based on linear and

morphological filtering.

The algorithm has been tested for images having

fixed resolution. For other resolutions different mask

sizes (M1 and M2, defined below) should be applied

when low-pass and high-pass filtering an image.

3.1 Image A

Image A provides the upper boundary of the cortical

bone. The algorithm consists of six steps; input

image is the ROI cut:

 High-pass filtering (M1 mask),

 Low-pass filtering (M1 mask), twice,

 Image brightness normalization,

 Thresholding

 Selection of the biggest object.

3.1.1 High-pass and Low-pass Filtering

A signal can be treated as the sum of low-pass and

high-pass components. Using this observation, high-

pass filtering can be done as follows:

J = I – LOWPASS(I, M1), (1)

where I is the original image, LOWPASS(I,M1)

means low-pass filtering of image I using mask M1.

The M1 mask is the matrix of 31x31 elements equal

to 1/31

, and has a notch filter characteristic.

Image J is low-pass filtered using the same mask

M1, the operation is performed twice. It leads to

boundary adjustment (less roughness), but some

blurring, which is corrected in next steps. The use of

a too small mask leads to important roughness of

boundaries after thresholding operation. Of course,

double low-pass filtering can be replaced by a single

one at the expense of increased computational time.

A SIMPLE METHOD OF CORTICAL BONE THICKNESS EVALUATION BASED ON RADIOGRAPHIC IMAGES

FOR OSTEOPOROSIS INVESTIGATION

271

3.1.2 Brightness Normalization

The next processing step relies on image brightness

normalization. 5th and 95th percentiles of image

histogram are computed and the L and H thresholds

are obtained. Pixels are assigned an intensity of zero

or one (maximum) if their brightness is below or

above thresholds L and H respectively. If the pixel

intensity is between L and H, a new pixel brightness

score is assigned according to the equation

()

L-y)IN(x,

L-H

y)OUT(x, ⋅=

, (2)

where OUT is the output image, IN describes the

input image, (x,y) are a pair of coordinates. This is a

simple linear transformation which leads to contrast

improvement in the interval <L,H>.

3.1.3 Thresholding

Only one global threshold is used, as experiments

have shown good results have been obtained for

threshold values T = 175/255 or T = 180/255. It

should be emphasized that more accurate boundary

determination is ensured for a variable threshold, but

the algorithm is not fully automatic in such case.

Image thresholding based solely on highpass

filtering (one global threshold) doesn’t give good

results, as artifacts tend to appear (many twigs). In

such cases upper boundary extraction is difficult.

3.1.4 Selection of the Biggest Object

At this point the (binary) image contains many small

structures, so the next step is to erase all objects but

the one with the biggest surface (structures surfaces

should be computed). An example is presented in

figure 3. Upper part of its contour is the desired

boundary to be extracted.

Figure 3: Example of image A.

3.2 Image B

Image B provides the lower boundary of the cortical

bone. It is much better visible than the upper one, as

the lower boundary occurs in the region of greater

contrast. The algorithm consists of six steps:

• Opening (mask 5x5),

• Low-pass filtering (mask M2),

• High-pass filtering (mask M1),

• Image brightness normalization,

• Thresholding,

• Selection of the biggest object.

Initially the opening operation is carried out

using a 5x5 window (all its elements equal to one),

which involves two nonlinear filtering steps: a

minimum filtering and a maximum filtering. A low-

pass filtering mask M2 consists of 21x21 elements

each having the value 1/21

. At this stage the image

is blurred. High-pass filtering, which is the next step,

emphasizes brightness differences and involves the

use of the previously defined M1 mask. The image

normalization stage has been described in section

3.1.2. Thresholding is performed using a global

threshold T2 equal to 0.35, as a result a binary image

is received. The biggest object is selected in the next

step, its upper limit is the lower cortical bone

boundary. A result is shown in figure 4.

Figure 4: Example of image B (same case as in figure 3).

Figure 5: Boundaries from Figures 3 and 4 superimposed

on the original image.

HEALTHINF 2009 - International Conference on Health Informatics

272

3.3 Contour Extraction

The algorithm combines boundaries of images A and

B. An exemplary result is shown in figure 5.

A and B images are inputs to the contour

extraction method. RESULT is the result image,

additionally, TEMP_TAB and POINTS tables are

used, k and j are indices; at the beginning k and j

equal one, while RESULT, TEMP_TAB contain

zeros. The size of the RESULT image is the same

and equal the size of the A image. The size of the

TEMP_TAB equals the column number of the image

A, the size of the POINTS table equals zero or one.

LAST is the variable determing the number of

column of image A.

1. Find the first white pixel in the k-th column in

the image A (searching is done from the last

row to the first one).

2. Find the first white pixel in the k-th column in

the image B (searching is done from the first

row to the last one).

3. If both pixels are found, execute the following

tasks and go to step 7: join them by the shortest

path (set of white pixels along the k-th column),

mark the connection in the image A (put white

pixel), TEMP_TAB[k]=1, check if the

difference between TEMP_TAB[k] and

TEMP_TAB[k-1] equals one, if it does, put

current k value to the table POINTS.

4. If none of pixels is found, go to step 7.

5. If the white pixel from the image B is not found

and the white pixel from image A is found,

execute following tasks and go to the step 7:

find the first white pixel in the k-th column of

the image A (searching is done from the first

row to the last row), remove all white pixels

from column k (put black pixels), with the

exception of the first white pixel found.

6. If the white pixel from the image B is found and

the white pixel for the image A is not found,

mark it in the A image (put white pixel) and

continue (go to step 7).

7. k = k +1, if k≤LAST, go to step 1, otherwise

continue.

8. Fill any holes in the image A.

9. Create RESULT image by extracting perimeter

of image A (RESULT= PERIMETER(A)).

10. Find all indices {m} for which TEMP_TAB[m]

– TEMP_TAB[m-1] equals -1, put them to the

separate cells of the POINTS table, if the size of

the POINTS table is greater than zero, go to the

next step, otherwise stop the algorithm.

11. Find the first white pixels in the POINTS[j]-th

column from the bottom and from the top of the

image.

12. Assign zero values in the RESULT image to the

pixels between pixels found (along the

POINTS[j]-th column), j = j +1, if j is greater

than the size of POINTS table, stop the

algorithm, otherwise go to step 11.

The flowgraph of the contour extraction algorithm is

shown in figure 6.

4 RESULTS

Forty images have been tested. The cortical bone

contours were extracted. Thresholds T=175/255 and

T=180/255 were used for the right and left side of

the dental panoramic radiograph respectively (image

A). The resulting boundaries have been presented to

a radiologist for verification and have been either

accepted or rejected. There is an irremovable

element of subjectivity in such a test, boundaries

sketched by a human aren’t absolutely strict, and

differ slightly from an evaluation session to another

one.

Table 1: The upper boundary, the left side.

Clutter free (N=28) Cluttered (N=12)

Accepted 26 Accepted 4

Rejected 2 Rejected 8

Table 2: The lower boundary, the left side.

Clutter free (N=28) Cluttered (N=12)

Accepted 28 Accepted 8

Rejected 0 Rejected 4

Table 3: The upper boundary, the right side.

Clutter free (N=31) Cluttered (N=9)

Accepted 30 Accepted 4

Rejected 1 Rejected 5

Table 4: The lower boundary, the right side

Clutter free (N=31) Cluttered (N=9)

Accepted 31 Accepted 5

Rejected 0 Rejected 4

Tables 1, 2 and 3, 4 present verification results

concerning the upper and lower cortical bone

boundaries for the left and right side, respectively.

Images have been classified either as cluttered or

clutter free. The cluttered images contain structures

which overlap the upper or lower cortical bone.

A SIMPLE METHOD OF CORTICAL BONE THICKNESS EVALUATION BASED ON RADIOGRAPHIC IMAGES

FOR OSTEOPOROSIS INVESTIGATION

273

There have been 12 and 9 images in which other

structures overlapped left or right side of DPR,

respectively.

As can be seen, in the case of clutter-free images

the results for extraction of cortical bone boundaries

have been from very good (26 correct ones out of 28

possible for upper boundary, left side) to perfect

ones (both lower boundaries). In contrast, results for

cluttered images are rather poor. Note however that

such images are easily discernible from the clutter-

free ones. Moreover, whenever the method have

failed, it has been very clear even for a non-

specialist that the extracted boundaries did not

define the cortical bone.

The particularly good results for the lower

cortical bone extraction result from higher contrast

at the edge of cortical bone. In the region of the

upper boundary of cortical bone the contrast is

usually much lower due to the presence of spongy

bone. In some cases when positioning of the patient

during x-ray examination was not performed

correctly, the superimposition over the upper cortical

boundary of other anatomical structures such as

hyoid bone was observed in the form of "clutter". In

a few cases the exact location of the upper cortical

border was uncertain even to the radiologist due to

factors mentioned above.

When comparing with existing methods (Devlin

et al., 2007) note that the algorithm presented is

neither complex nor a time consuming one. Firstly,

in contrast to the method based on snakes it is non-

iterative, results are obtained in a single run. Time

complexity of each of its steps is O(n), i.e. the

smallest possible. The prototype function written in

MATLAB (version 7.0) realizing the algorithm

executed in 0.4s for one image on 1.6 GHz Intel

Celeron with 1GB RAM, an optimized program

would be an order of magnitude faster. The snakes

are moving across an image, the computation of a

dislocation for each segment of a snake requires

solving some equilibrium equations. Of course, it

might be done quite time-effectively, if precision

need not be high. Unfortunately, the method from

(Devlin et al., 2007) forms a basis for a commercial

software, hence, the details are not known.

When image contains structures that overlap the

upper cortical bone, thresholding often do not lead to

correct extraction. Note, however that unless a

method has a human-like ability to draw a known

shape on the basis of its small fraction, correct bone

extraction in heavily cluttered images is a hopeless

task. Straightforward use of snakes does not

guarantee the success, too. That is why a clearly

wrong outline of a cortical bone in such images

seems to be a much better result than a shape that is

probable, but highly imprecise one.

6 CONCLUSIONS

A new simple and effective algorithm for extracting

cortical bone boundaries has been described in the

paper. It consists of elementary operations available

as functions in every image processing software

package. The method works very well for clutter-

free images, on the other hand, it is very clear when

it fails in cases when the image is highly misleading.

This combination of features is ideal for an

untrained algorithm user, hence, the method is an

excellent auxiliary tool for osteoporosis

investigation by general dentist practitioners.

As it has been mentioned in the introduction, the

proposed algorithm can be used for the cortical bone

width determination, which seems to be useful for

identification of women with low BMD level (Arifin

A. et al., 2006). Future work will be concentrated on

automatic cortical bone width measurement based

on the proposed algorithm.

REFERENCES

Tosoni, G.M., Lurie, A.G., Cowan, A.E., Burleson, J.A.,

2006. Pixel intensity and fractal analyses detecting

osteoporosis in perimenopausal and postmenopausal

women by using digital panoramic images. In Oral

Surgery, Oral Medicine, Oral Pathology, Oral

Radiology, and Endodontics. Vol. 102(2), pp. 235-

241.

Horner K., Devlin H., Harvey L., 2002. Detecting patients

with low skeletal bone mass. In J. Dent. Vol. 30, pp.

171-175.

Devlin H., Allen P.D., Graham J., Jacobs R., Karayianni

K., Lindh C., van der Stel P.F., Harrison E., Adams

J.E., Pavitt S., Horner K., 2007. Automated

osteoporosis risk assessment by dentists: A new

pathway to diagnosis. In Bone. Vol. 40, pp. 835–842.

Devlin C.V., Horner K., Devlin H., 2001. Variability in

measurement of radiomorphometric indices by general

dental practitioners. In Dentomaxillofac Radiol. Vol.

30, pp. 120-125.

Arifin A. Z.,Asano A., Taguchi A., Nakamoto T., Ohtsuka

M., Truda M., Kudo Y., Tanimoto K., 2006.

Computer-aided system for measuring the mandibular

cortical width on dental panoramic radiographs in

identifying postmenopausal women with low bone

mineral density. In Osteoporosis International, Vol.

17, pp. 753–759.

HEALTHINF 2009 - International Conference on Health Informatics

274

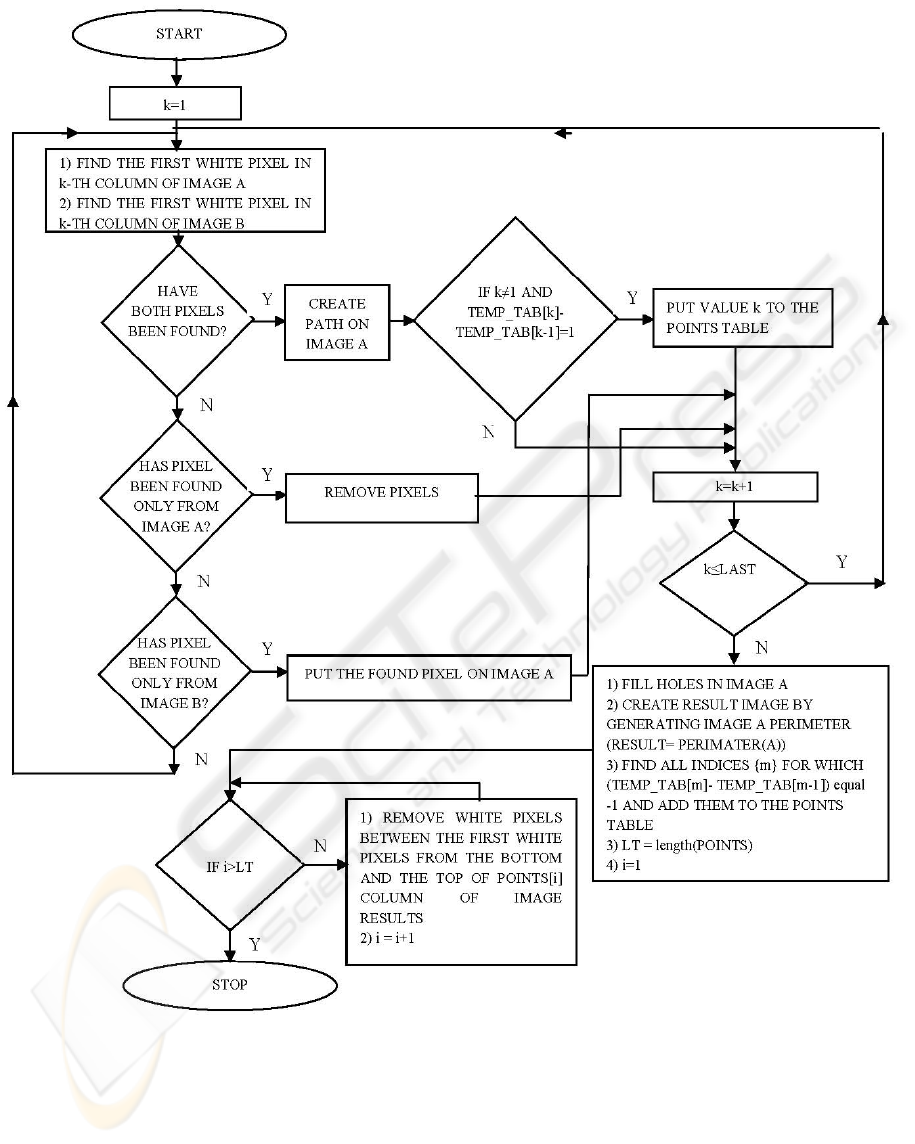
Figure 6: The flowchart of the contour extraction method.

A SIMPLE METHOD OF CORTICAL BONE THICKNESS EVALUATION BASED ON RADIOGRAPHIC IMAGES

FOR OSTEOPOROSIS INVESTIGATION

275