DESIGN OF A BIO-INSPIRED WEARABLE EXOSKELETON

FOR APPLICATIONS IN ROBOTICS

Michele Folgheraiter, Bertold Bongardt, Jan Albiez and Frank Kirchner

German Research Center for Artiﬁcial Intelligence DFKI Bremen

Robotics Lab Robert-Hooke-Strae 5D-28359 Bremen, Germany

Keywords:

Haptic Interface, Bio-Inspired Device, Biorobotics, Exoskeleton.

Abstract:

In this paper we explain the methodology we adopted to design the kinematics structure of a multi-contact

points haptic interface. We based our concept on the analysis of the human arm anatomy and kinematics with

the intend to synthesize a system that will be able to interface with the human limb in a very natural way. We

proposed a simpliﬁed kinematic model of the human arm using a notation coming from the robotics ﬁeld. To

ﬁnd out the best kinematics architecture we employed real movement data, measured from a human subject,

and integrated them with the kinematic model of the exoskeleton , this allow us to test the system before its

construction and to formalize speciﬁc requirements. We also implemented and tested a ﬁrst passive version of

the shoulder joint.

1 INTRODUCTION

In this paper a bio-inspired design approach to syn-

thesize the kinematics structure of a haptic interface is

introduced. The system presented is mainly intended

for applications in the ﬁeld of the tele-robotics sys-

tems; nevertheless can also be effectively employed

as a sophisticated haptic interface during the interac-

tion with a virtual environment or during a training or

rehabilitation session.

In interaction with a human an exoskeleton can

provide two main functionalities: First, it can be used

as an assistive device, e.g in physiotherapy an ex-

oskeleton can be adopted for movement enhancement

(Gupta et al., 2008) (Carignan et al., 2005), in other

scenarios it can be used for performance augmenta-

tion (Dollar and Herr, 2008).

Second, an exoskeleton can be used as an input

device, enabling a human operator to manipulate ei-

ther a virtual or a real target system. The latter use-

case – which is called teleoperation surrenders in any

situation where work has to be done in regions, in

which it is unfavorable or even impossible to work as

a human. Possible applications for teleoperation oc-

cur in telesurgery (Bar-Cohen et al., 2001), aerospace

(Schiele and Visentin, 2003) and underwater (Kwon

et al., 2000).

The primary aim of an intuitive teleoperation is to

allow a human operator to see and feel the remote en-

vironment, as a secondary aim he further should be

able to attribute himself with the target robot (IJssel-

steijn et al., 2006). A general overview about the topic

of teleoperation is given in (Hokayem and Spong,

2006).

In case of teleoperation an exoskeleton acts as an

human-robot haptic interface which is “nothing but

a bidirectional mechanical transducer”(Hayward and

Astley, 1996). Ciriteria for the quality of haptic feed-

back are given in (Hayward and Astley, 1996), com-

parative studies are are presented in (Grifﬁn et al.,

2005) or (Yu, 2003).

The hardware of existing constructions of ex-

oskeletons differ in their degree of activity: On the

one hand pure passive devices were developed by

(Song et al., 2005) and (Chen et al., 2007, ZJUESA).

On the other hand empowering exoskeletons were

built up, see (Dollar and Herr, 2008). Between

these extrema one ﬁnds exoskeletons acting as force-

reﬂecting controlling devices. These can be further

categorized into solutions which are ﬁxed to an exter-

nal basis (Mistry et al., 2005) and (Perry et al., 2007)

and those remaining wearable. The latter is described

by the study in (Kim et al., 2001).

In the next following section we introduce the

model used during the design process, we also

presents some results from the study we conducted

on a real human subject in order to analyse the impor-

tance of the Clavicle-Scapula articulation during the

414

Folgheraiter M., Bongardt B., Albiez J. and Kirchner F. (2009).

DESIGN OF A BIO-INSPIRED WEARABLE EXOSKELETON FOR APPLICATIONS IN ROBOTICS.

In Proceedings of the International Conference on Biomedical Electronics and Devices, pages 414-421

DOI: 10.5220/0001550704140421

 SciTePress

shoulder movement. Section 3 deals with the kine-

matic model of the exoskeleton, in particular here we

reported only the system that is supposed to be cou-

pled with the shoulder of the user. In section 4 we pro-

pose a possible design for the exoskeleton and present

some preliminary results. Finally section 5 draws out

the conclusions and the future developments.

2 HUMAN ARM STUDY

AND KINEMATIC MODEL

The Human Arm represents one of the most advanced

manipulation system we can ﬁnd in nature. It is the

product of an evolutionary process lasted 3.7 billion

years (origin of life on the Earth). Its kinematics is

deﬁned by the conﬁguration of different bones and

articulations, these elements represent the structural

components of the limb. Grossly we can divide the

arm in two different parts: the upper arm and the fore-

arm. The upper arm is represented by the segment that

goes from the shoulder to the elbow, the forearm the

segment that goes from the elbow to the hand.

Starting from the sternum (see picture 1), that for

us represent the reference base, and moving toward to

the distal part of the limb, we can encounter the fol-

lowing bones : Clavicle, Scapula, Humerus, Radius,

Ulna, Carpus Bones, Metacarpus Bones, Phalanxes.

Figure 1: Representation of the skeleton of the human

arm and its 10 DOF simpliﬁed kinematics model using a

robotics notation.

In literature we can ﬁnd different kinematic mod-

els for the human arm (Klopcar and Lenarcic, 2005),

(Schiele and van der Helm, 2006), each one oriented

to describe certain aspects rather than the others; As

in (Schiele and van der Helm, 2006), to represent the

kinematic model of the human arm, we used a no-

tation related with the robotics ﬁeld this in order to

couple it more easily with the kinematic model of the

exoskeleton. Of course we introduced numerous sim-

pliﬁcations and assumed the articulations like joints

with a well deﬁned geometry, nevertheless we think

that for our study this ﬁts well.

The model formalized is represented in ﬁgure 1

(right side), again we can separate the kinematic ar-

chitecture in two different parts: Shoulder Kinemat-

ics, Arm Kinematics. The shoulder Kinematics is

composed by four joints, three spherical (3DOF) and

one planar. More in detail the planar joint can be de-

composed in two prismatic and one rotational joint,

however in this ﬁrst representationwe preferredto use

a compact notation. It also should be noted that the

shoulder kinematics can be further separated in two

other parts: one that is a closed kinematic chain, and

the other that is an open kinematic chain represented

by a spherical joint located in the proximal part of the

upper arm link. The closed chain is formed by three

links and three joints, joint-1 (spherical) is located be-

tween link-0 (the link with the inertia reference sys-

tem) and link-1, joint-2 (spherical) is located between

link-1 and link-2, and ﬁnally joint-3 (planar) close the

kinematics chain connecting link-2 and link-0.

The ﬁrst consideration we can do on this kine-

matic chain is about the overall mobility. The three

joints have a total of 9 DOFs, however because of its

parallel nature there are some constrains that limit the

mobility. We can deﬁne q as the conﬁguration vari-

able, this is a vector with m components (q ∈ R

)

that deﬁne unambiguously the position and the ori-

entation of the all rigid bodies that compose the kine-

matic chain. We consider in this case only minimal

conﬁgurations, this means that is not possible deﬁne

unambiguously the system with less than m scalars.

Given the kinematic chain we can calculate the

dimension for q applying the Kutzbach-Gr¨ubler for-

mula (Zhao et al., 2004) :

m = 6(n− g− 1) +

∑

i=1

(1)

where n is the number of links present in the kine-

matic chain, g is the number of joints, and f

is the

number of degrees of freedom for the i

joint. If we

apply this equation to our speciﬁc case we obtain:

m = 6(3− 3− 1) +

∑

i=1

= −6+ 9 = 3 (2)

This mean that this chain has overall three de-

grees of freedom, therefore to deﬁne unambiguously

DESIGN OF A BIO-INSPIRED WEARABLE EXOSKELETON FOR APPLICATIONS IN ROBOTICS

415

its kinematic conﬁguration we can just deﬁne only

three scalars. The model differs from (Schiele and

van der Helm, 2006) for the presence of an addi-

tional DOF that allows to represents better the human

anatomy. The question that arise now is: which joints

variables we have to chose to deﬁne the conﬁgura-

tion of the shoulder, in theory it is possible to chose

just three variables from the nine we have. In practice

we will see that there are some choices that are bet-

ter than others, this especially if we need to measure

these quantities in a real system.

Starting from the joint-4 the human arm can be

represent as a open kinematic chain. As we can

see from picture 1 joint-4 (lower part of the shoul-

der) connects link-2 to link-3. This joint has a total

of three DOF and allows movements of extension-

ﬂexion, adduction-abduction and rotation around the

upper arm axis.

Moving toward the distal part of this model we

encounter joint-5 (the elbow) that connect link-3 with

link4, this is a one DOF rotational joint that allow

forearm ﬂexion and extension. Finally we have joint-

6 (ﬁrst degrees of freedom for the wrist) that connect

link-4 with link-5. In comparison with the human arm

anatomy this represent a simpliﬁcation, indeed in hu-

man beings it is a complex movement of both radio

and ulna bones that allows the wrist rotation. Any-

how in a ﬁrst approximation this simpliﬁcation is not

so critical for our purposes. A more accurate model

will be formalized in the case the results obtained will

be not satisfactory.

In picture 1 we represented also the other joint for

the wrist, joint-7, this has a total of two degrees of

freedom that in the human arm allow the wrist ﬂexion-

extension and adduction-abduction. At the moment

the hand kinematics is not considered in our study.

2.1 Analysis of the Arm Movements

In order to better understand the kinematic of the hu-

man Arm, and to start the validation of the proposed

model, we conducted a ﬁrst experiment where we ac-

quired the trajectories of different points of interest

located on the surface of the Arm. We applied a total

of 19 markers (see picture 2) on a male subject (height

1.7m.) 3 along the spinal cords, 3 on the scapula, 1

on the top of the shoulder, 3 for the shoulder ring, 1

in the middle of the upper arm, 3 in the elbow ring , 1

in the middle of the forearm, and 4 in the wrist ring.

We wanted to acquire the trajectories of all the parts

of the Arm that are involved during the performance

of an arbitrary movement. In the ﬁrst experiment we

asked the subject to perform a movement of ﬂexion

and extension of the shoulder. The rotation was rela-

tive to an hypothetical axes orthogonal to the sagittal

plane, of course due to the complex kinematic of the

shoulder this axes is not ﬁxed, but changes according

with the shoulder movements.

Figure 2: 19 Markers were ﬁxed on the surface of the sub-

ject’s arm.

The Experiment where done using a commercial

motion tracking system by Qualysis

, we employed

the version with three cameras.

We chose an arrangement in order to avoid as

much as possible the landmarks occlusion during the

planned movement.

During the acquisition subject was located near

the reference system, and was asked to perform the

movement of the arm trying to keep ﬁxed as much as

possible the rest of the body.

After data acquisition and post-processing, it was

possible to analyze the results visually, and to ex-

port the data in text format for a further elabora-

tion by Matlab. The analysis of the movement by

the QualysisTrackManager

showed many interest-

ing features and behaviors. We noted that from the

ﬁrst phase of the extension movement all the bones

of the upper shoulder are involved. We could recog-

nize this by observing the trajectory of the markers

located on the top of the shoulder, and in proximity of

the scapula (ﬁgure 3a ).

This means that it is very difﬁcult to separate the

movement of the lower shoulder from the movement

of the upper shoulder, it turns out that we need to con-

sider the entire shoulder kinematics from the begin-

ning of the exoskeleton design. In picture 3 (b) we

can see the trajectories followed by the markers for

quite the complete extension movement (90%), it ap-

pears that many of them have a circular pattern, this

is natural if we think at the kinematic structure of the

human shoulder.

BIODEVICES 2009 - International Conference on Biomedical Electronics and Devices

416

a. b.

Figure 3: (a)First part of the movement, it possible to note

that the markers on the top of the shoulder start to move (b)

Trajectories followed by the markers during the 90% of the

extension movement.

3 THE EXOSKELETON

KINEMATIC

The exoskeleton kinematics is strongly inﬂuenced

both by the human arm anatomy and the perfor-

mances we want to reach. The central idea is to try

to restrict the mobility of the user’s arm as less as

possible when he is wearing the exoskeleton. Other

desiderable requirements for the overall system are:

• Lightweight construction

• A system easily wearable

• Multi-contact points haptic feedback

• Modular design

All these goals are important to synthesize the

kinematic structure for the exoskeleton, but for an ini-

tial analysis, the overall mobility constrains and the

necessity to have multi-contact point haptic interface,

represent our most relevant aims.

If we want to reduce the user’s mobility limita-

tions due to the exoskeleton we can ﬁx the following

kinematic requirements:

• The upper arm coupled with the upper part of the

exoskeleton should have a total of 3 DOFs

• The forearm coupled with the lower part of the

exoskeleton should have a total of 2 DOFs

In order to provide the user a broad haptic feed-

back, our exoskeleton will transmit forces and torques

via multiple contact points. One of these we have

already deﬁned locating the exoskeleton-shoulder on

the user-shoulder, the other will be located in the mid-

dle of the user upper arm and the last one in the middle

of the user forearm. This locations are optimal in the

sense that they reduce the interference with the hu-

man articulation during the user movements. One can

see these three different contact-points represented in

ﬁgure 4.

Contact Point 1

Contact Point 2

Contact Point 3

Figure 4: Contact points between the exoskeleton and the

human arm.

3.1 Coupling the Exoskeleton with the

Human Arm

It is important now to do some considerations about

the overall kinematics that we obtain combining the

arm with the exoskeleton. This will also help us to

setup how many degrees of freedoms are required for

the exoskeleton.

The next paragraph will concentrate only on the

exoskeleton’s kinematics that deals with the shoulder

and the upper arm of the user, even if we have al-

ready started to extend the analysis also for the fore-

arm. This omission is also justiﬁes by the fact that at

the moment we tested on a human subject only this

part of the exoskeleton.

3.1.1 The Upper Shoulder Joint

Here we the term joint we want to refer to the en-

tire kinematic structure for the mechanical system that

is charged to deal with the upper shoulder (clavicle-

scapula articulation). How many degrees of freedom

should have this joint? From the motion analysis on

the human arm it comes up that the upper shoulder

has a total of 3DOF, but again in order to design the

exoskeleton joint it is necessary to do some assump-

tions about its kinematics. A possible conﬁguration

is presented in ﬁgure 5 (upper part) here we can see

that now we have a complex structure with different

closed paths.

In order to study the system we can do a ﬁrst sim-

pliﬁcation substituting the upper shoulder kinematic

with a single joint with 3 DOF, in this case we have a

simpliﬁed structure showed in ﬁgure 6.

Now it is possible to apply the theory in order to

ﬁnd the overall mobility of this conﬁguration, we can

calculate the number of DOF’s with equation 3.

m = 6(n− g−1) +

∑

i=1

= 6(5− 5−1)+ 9 = 3 (3)

DESIGN OF A BIO-INSPIRED WEARABLE EXOSKELETON FOR APPLICATIONS IN ROBOTICS

417

3DOF

J 1

J 2

J 3

3DOF

L 0

L 2

L 3

Figure 5: Closed kinematic chain formed between the ex-

oskeleton shoulder joint and the upper shoulder kinematic

chain.

2DOF

3DOF

L 0

J 1

L 2

J 3

L 1

J 2

2DOF

1DOF

L 2

L 1

1DOF

Figure 6: Equivalent model.

As is represented in ﬁgure 6 the exoskeleton has

a total of 6 DOF; because we need to actuate a 3

DOF kinematic chain, it means that only 3 of the 6

DOF must be actuated and sensed. From a mechan-

ical point of view it is more suitable to actuate the

joints (J

1 and J

2) that is near to the barycenter of

the body, in this way the actuation system is not re-

quired to move also the weigh of the actuators itself,

this come clear if you think to the torque that can ex-

ercise a weight localized near the joint J

3 to the joint

3.1.2 Model Simulations

To ﬁx some speciﬁcations for the actuation system of

the exoskeleton we formilized a kinematic-dynamic

model of the exoskeleton shoulder-joint using the

toolbox SimMechanics in Matlab-Simulink environ-

ment. The system is composed of a spherical joint

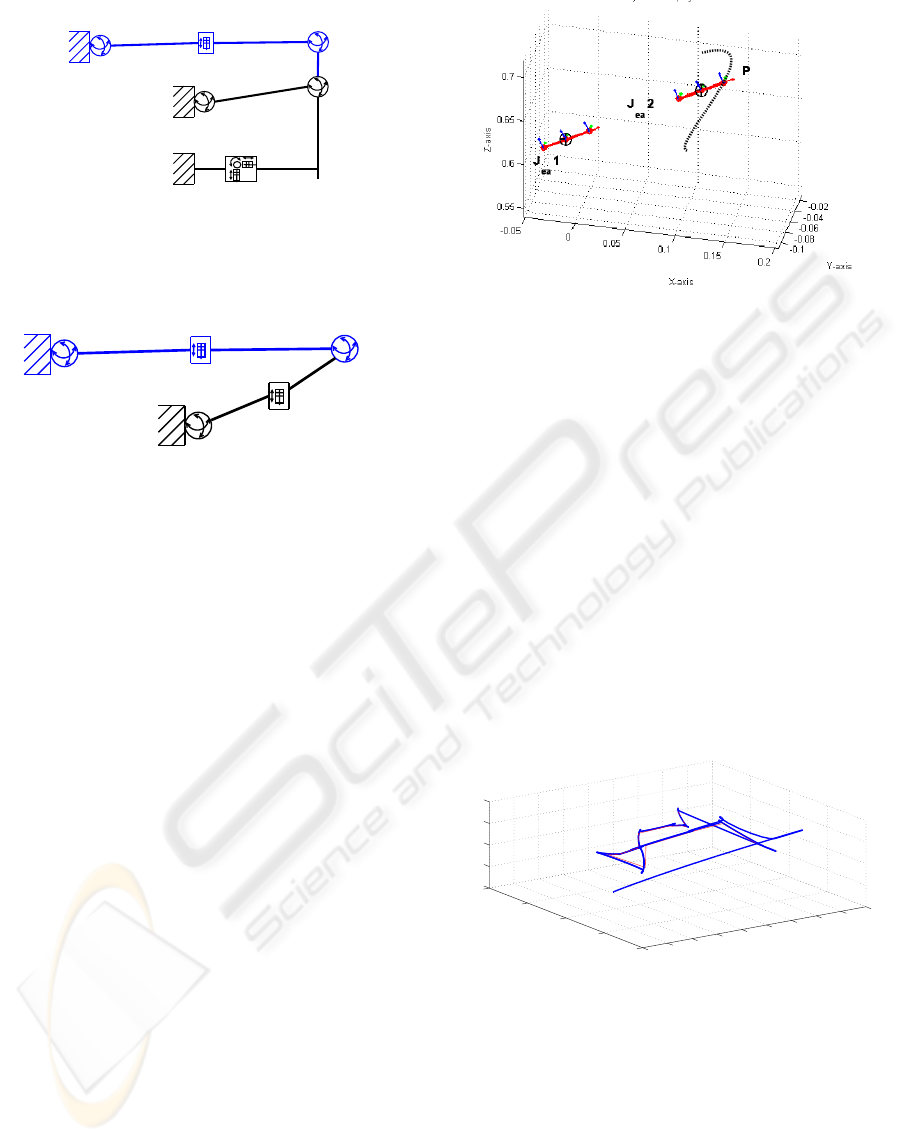
and a prismatic joint (see picture 7).

The initial point for the exoskeleton joint is coin-

cident with the middle landmark along the spinal cord

(see section 2.1).

In order to analyze the motion in a realistic way,

we constraint the point P (see picture 7 ) to lie on a

trajectory. We imposed as a trajectory the one we ob-

tained from the motion analysis of the human arm per-

forming an extension-ﬂexion movement of the shoul-

der (underlined Marker in picture 2). To constrain

the point on the desired trajectory we apply a force

ﬁeld directly on the point that was generated using a

MIMO (Multi Input Multi output) PID controller, pa-

Figure 7: Simulation for the Shoulder Joint, measures in

meters.

rameters of this controller were not optimized because

we wanted only to perform a kinematical test of the

system. The PID in question can be represented using

a diagonal matrix:

P=0.4,I=0.1,D=0.3 0 0

0 P=0.4,I=0.1,D=0.3 0

0 0 P=0.4,I=0.1,D=0.3

This means that only the position error along the

X-axis will effect the X-component of the force, and

the same for error along Y- and Z-axis. The results of

this simulation is reported in picture 8, as it possible

to see the force ﬁeld generated is able to constrain

the point trajectory (thicker line) near the reference

trajectory (thin line).

0.02

0.04

0.06

0.08

0.1

0.12

0.14

0.16

0.18

0.2

−0.1

−0.08

−0.06

−0.04

−0.02

0.55

0.6

0.65

0.7

0.75

Figure 8: The trajectory followed (thicker line) by the point

located on the upper shoulder, the thin line is the reference

trajectory acquired from a human subject.

Once we are sure that point P is well constrained

we can monitoring the position of each joint of the ex-

oskeleton in order to evaluate the range of its move-

ment, this is very useful to obtain same speciﬁcations

for the design of the real system. In the graph of pic-

ture 9 we can see the linear position of the prismatic

joint, how it is possible to note the range for this sub-

ject is about 0.08m (8cm). Of course it is necessary to

BIODEVICES 2009 - International Conference on Biomedical Electronics and Devices

418

perform this analysis on different subjects if we want

to have a system that can adapt to different arm sizes,

this will be the subject of future work.

0 50 100 150 200 250 300

0.02

0.04

0.06

0.08

0.1

0.12

0.14

0.16

Sample

Position [mm]

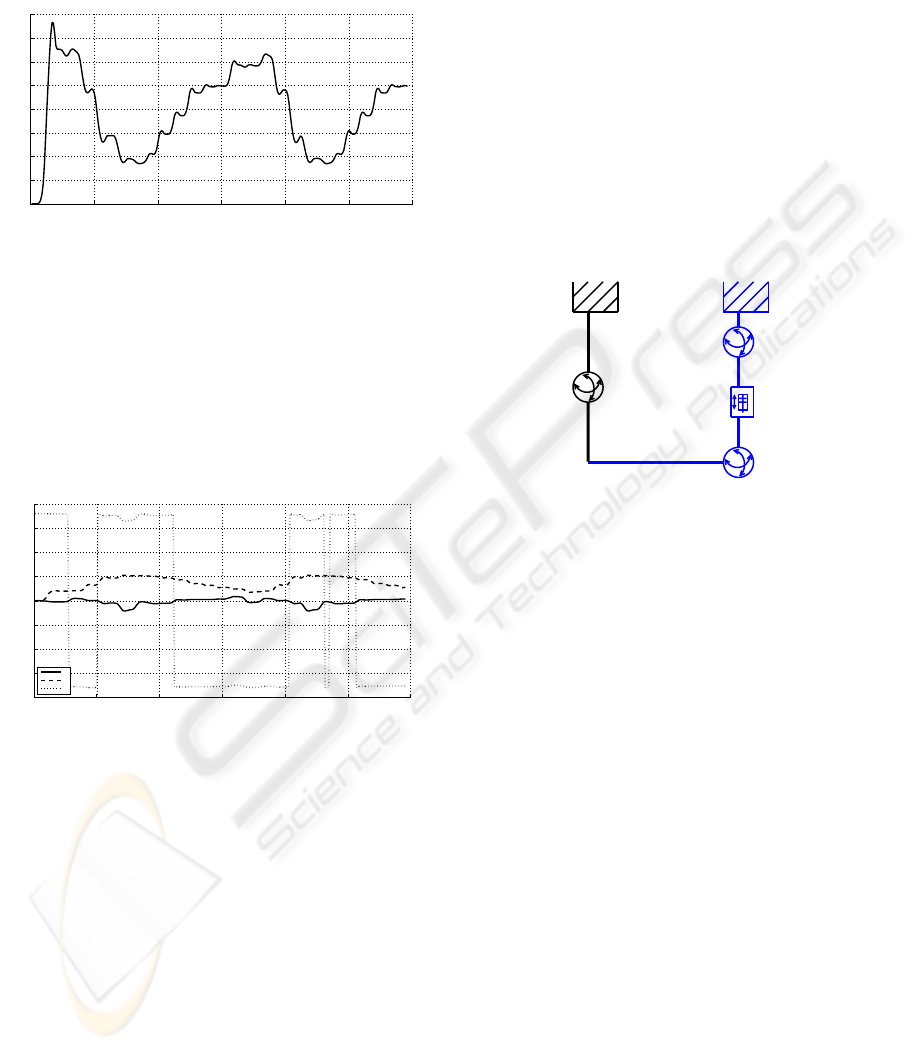
Figure 9: Range for the prismatic joint.

Figure 10 reports the angular positions of the

spherical joint in convention of the Euler angles (roll,

pitch and yaw). Therefore if we want to obtain the an-

gular position of the exoskeleton we should do in se-

quence three rotations along X,Y and Z respectively.

Again we can evaluate the excursion for each sin-

gle angle, from ﬁgure 10 we can see that roll range is

about 30

, the pitch 50

and ﬁnally the yaw 15

0 50 100 150 200 250 300

−200

−150

−100

−50

100

150

200

Sample

Angular position [Degrees]

Figure 10: The three Euler Angles for the spherical joint.

3.1.3 Lower Shoulder Joint

Considering the lower shoulder (upper arm) com-

bined with the upper part of the exoskeleton (ﬁgure

11) one can identify a closed kinematic chain. It

starts at the link L

0, crosses join J

1 (the user shoul-

der), goes toward the contact point one (where the ex-

oskeleton is ﬁxed with the user upper arm) and then

encounters in the order J

3, J

2 and J

1 that belong

to the exoskeleton. Finally the kinematic chain ends

with the link L

0 that in this case coincides with L

We have also to observe that in picture 11 L

1 and L

should be considered as a single link. Supposing now

that J

1 is a 2DOF rotational joint, J

2 is a 1DOF

prismatic joint and J

3 a spherical joint we can cal-

culate the overall degrees of freedom of this closed

kinematics.

m = 6(n− g−1) +

∑

i=1

= 6(4− 4−1)+ 9 = 3 (4)

Equation 4 shows that combining the exoskeleton

with the arm brings to a system that has three degrees

of mobility (user upper arm), of course this do not

guarantee that the mobility we obtain is similar to the

mobility of the user upper arm. This is due to the

fact that Kutzbach-Gr¨ubler formula do not takes in ac-

count the conﬁguration of the joint, but only the total

number of joints and degrees of freedom. For a more

precise analysis, a possible solution is to perform a se-

ries of simulations, this will hallow us also to explore

different conﬁgurations with different parameters.

L 0

L 1

J 1

L 0

L 1

J 1

J 2

L 2

J 3

L 3

Figure 11: Kinematic representation of the exoskeleton

coupled with the user upper arm.

4 EXOSKELETON DESIGN

From the data analysis of the extension/ﬂexion move-

ments of the shoulder it clearly appears that it is nec-

essary to consider the overall shoulder complexity in

order to deﬁne the exoskeleton kinematic.

However, in order to simply the design process,

it is still possible to assume the point deﬁned on the

upper-lateral part of the shoulder as a starting point

where to ﬁx the kinematic structure that will follow

the lower shoulder movements.

Therefore we separated the exoskeleton design in

two different parts: one that deals with the upper and

the other with the lower shoulder. In the following

we explain a possible solution for the upper shoulder

joint.

4.1 Upper-shoulder Joint

The mechanical structure is composed by four joints:

a sequence of two rotational, one prismatic and one

spherical joints. In ﬁgure 12 we can see a ﬁrst con-

cept for this structure, were we can note that there are

two connection structures: one that is intended to be

ﬁxed to the user pelvis (the belt), and the other that is

DESIGN OF A BIO-INSPIRED WEARABLE EXOSKELETON FOR APPLICATIONS IN ROBOTICS

419

intended to be connected with the top side of the user

shoulder. We want to employ rigid materials for these

two parts in order to have a stable connection with

the human body, but of course, we need also to shape

these parts in order to be comfortable for the user.

2DOF

3DOF

L 0

J 1

L 2

J 3

L 1

J 2

2DOF

1DOF

L 2

L 1

1DOF

Active DOF’s

Passive DOF’s

Figure 12: The Upper-Shoulder joint Exoskeleton concept

and its kinematic structure.

exoskeleton. It is quite easy to ﬁx the belt to the

pelvis.

To design the device we should also take into ac-

count some important parameters:

• The exoskeleton length: this parameter should be

adjustable in order to ﬁt with different user sizes.

Fortunately the length depends on the linear posi-

tion of the prismatic joint, this means that the joint

movement can be used to control the position of

the user shoulder but also to adjust the device to

the user size.

• The distance between the exoskeleton and the user

back: this is important because if the exoskeleton

is too near to the user back collisions will occur

during the shoulder movements.

• The Shoulder-Connection dimension: this also

depend on the size of the user shoulder, in this

case it is necessary to build up a mechanism

adaptable. A possible solution is to use an inﬂat-

able device, even if this will decrease the stability

of the contact point.

Furthermore in order to keep low the inertia and

the torque requirements of the actuation system, we

can think to actuate the ﬁrst three DOF and let pas-

sive the last three (Spherical Joint). This solution is

also optimal for the mass distribution, in this case the

barycenter is more near to the user spinal cords (the

endoskeleton that sustains all the upper body weight).

To evaluate if the kinematic structure we assumed

for the exoskeleton is suitable and efﬁcacious, we de-

cided to build a passive version of the system. This,

depicted in ﬁgure 13, reproducesthe same mechanical

functionality of the system until the lower-schoulder-

Joint, but has only sensory capabilities, indeed no ac-

tuators are mounted on the joints. We tested the de-

vices on different subjects and we get a ﬁrst impres-

sion on how the system works.

Figure 13: The passive version of Upper and Lower

Shoulder-joint.

From this ﬁrst qualitative analysis we obtain a

very usefull feedback in order to guide the next steps

for the design process. We noticed that the dimen-

sions of the different exoskelton’s links are not only

important to ﬁt the size of different users, but are

also critical to keep the joints movements in a proper

range. For example, if the link L

2 (picture 12) is

too long the prismatic joint is always completely re-

tracted. This initial condition brings the system to

lose some degrees of mobility. A solution for this

problem is to dimension the exoskeleton in a manner

that each joint, in its initial state, assumes a position

in the middle of the possible range.

5 CONCLUSIONS AND FUTURE

WORK

In this paper we described the design methodologywe

adopted to develop a multi contact point haptic inter-

face. We introduce a kinematic model for the human

arm and combine it we real motion data in order to

synthesize the exoskeleton. We show by realistic sim-

ulations that the kinematic conﬁguration we chose for

the shoulder-joint ﬁts with the human arm anatomy

and do not restrict the shoulder movement. Future

work will be ﬁnalized to better study the kinematics

of the system that will deal with lower shoulder and

the forearm and to test a complete arm-prototype. We

BIODEVICES 2009 - International Conference on Biomedical Electronics and Devices

420

need also to solve the problem of designing a stable

interface between the exoskeleton and the arm and to

develop a proper actuation system. At the movement

we are dealing with the experimentation of a light hy-

brid hydraulic-pneumatic actuator that will be able to

ﬁnally control the force feedback and to change the

impedance actively.

REFERENCES

Bar-Cohen, Y., Mavroidis, C., Bouzit, M., Dolgin, B.,

Harm, D. L., Kopchok, G., and White, R. (2001).

Virtual reality robotic telesurgery simulations using

memica haptic system. In Electroactive polymer ac-

tuators and devices, SPIE proceedings series, volume

4329, pages 357–363.

Carignan, C., Liszka, M., and Roderick, S. (2005). Design

of an arm exoskeleton with scapula motion for shoul-

der rehabilitation. Advanced Robotics, 2005. ICAR

’05. Proceedings., 12th International Conference on,

pages 524–531.

Chen, Y., Zhang, J., Yang, C., and Niu, B. (2007). The

workspace mapping with deﬁcient-dof space for the

puma 560 robot and its exoskeleton arm by using or-

thogonal experiment design method. Robot. Comput.-

Integr. Manuf., 23(4):478–487.

Dollar, A. and Herr, H. (2008). Lower extremity exoskele-

tons and active orthoses: Challenges and state-of-the-

art. Robotics, IEEE Transactions on, 24:144–158.

Grifﬁn, W. B., Provancher, W. R., and Cutkosky, M. R.

(2005). Feedback strategies for telemanipulation with

shared control of object handling forces. Presence:

Teleoper. Virtual Environ., 14(6):720–731.

Gupta, A., O’Malley, M. K., Patoglu, V., and Burgar, C.

(2008). Design, control and performance of ricewrist:

A force feedback wrist exoskeleton for rehabilitation

and training. Int. J. Rob. Res., 27(2):233–251.

Hayward, V. and Astley, O. (1996). Performance mea-

sures for haptic interfaces. In Giralt, G. and Hirzinger,

G., editors, Robotics Research: The 7th International

Symposium, pages 195–207. Springer Verlag.

Hokayem, P. and Spong, M. (2006). Bilateral teleoperation:

An historical survey. Automatica, 42:2035–2057.

IJsselsteijn, W. A., de Kort, Y. A. W., and Haans, A. (2006).

Is this my hand i see before me? the rubber hand illu-

sion in reality, virtual reality, and mixed reality. Pres-

ence: Teleoper. Virtual Environ., 15(4):455–464.

Kim, Y. S., Lee, S., Cho, C., Kim, M., and Lee., C.-W.

(2001). A new exoskeleton-type masterarm with force

reﬂection based on the torque sensor beam. Robotics

and Automation – Proceedings 2001 ICRA. IEEE In-

ternational Conference on, 2623:2628–2633.

Klopcar, N. and Lenarcic, J. (2005). Kinematic model

for determination of human arm reachable workspace.

Meccanica, (40):203219.

Kwon, D.-S., Ryu, J.-H., Lee, P.-M., and Hong, S.-W.

(2000). Design of a teleoperation controller for an

underwater manipulator. In Robotics and Automa-

tion, 2000. Proceedings. ICRA apos;00. IEEE Inter-

national Conference on, pages 3114–3119.

Mistry, M., Mohajerian, P., and Schaal, S. (2005). An ex-

oskeleton robot for human arm movement study. In

Intelligent Robots and Systems, 2005. (IROS 2005).

2005 IEEE/RSJ International Conference on, pages

4071– 4076.

Perry, J., Rosen, J., and Burns, S. (2007). Upper-limb pow-

ered exoskeleton design. Mechatronics, IEEE/ASME

Transactions on, 12:408 – 417.

Schiele, A. and van der Helm, F. (2006). Kinematic design

to improve ergonomics in human machine interaction.

Neural Systems and Rehabilitation Engineering, IEEE

Transactions on, 14(4):456–469.

Schiele, A. and Visentin, G. (2003). The esa human arm

exoskeleton for space robotics telepresence. In 7th

International Symposium on Artiﬁcial Intelligence,

Robotics and Automation in Space, iSAIRAS.

Song, D. H., Lee, W. K., and Jung, S. (2005). Control

and interface between an exoskeleton master robot

and a human like slave robot with two arm. In Ad-

vanced Intelligent Mechatronics. Proceedings, 2005

IEEE/ASME International Conference on, pages 319–

324.

Yu, A. B. (2003). A taxonomy and comparison of haptic

actions for disassembly tasks.

Zhao, J.-S., Zhou, K., and Feng, Z.-J. (2004). A theory of

degrees of freedom for mechanisms. Mechanism and

Machine Theory, 39(6):621–643.

DESIGN OF A BIO-INSPIRED WEARABLE EXOSKELETON FOR APPLICATIONS IN ROBOTICS

421