INSECT NAVIGATION BY POLARIZED LIGHT
F. J. Smith
School of Electronics, Electrical Engineering and Computer Science, Queens University, Belfast, N. Ireland
Keywords: Polarization, Skylight, Navigation, Clouds, POL, Insect celestial map, Robot navigation.
Abstract: Many insects can navigate accurately using the polarized light from the sky. A study of a large number of
experiments on the behaviour and anatomy of insects has led to a simple algorithm for navigation by
skylight, suitable for a robot or drone in lightly clouded skies. The algorithm is based on the special ability
of insect eyes to measure the position of the 4 points in the sky at which the polarization angle, i.e. the angle
χ between the polarized E-vector and the meridian, equals ±π/4. The azimuths of these 4 points are possibly
the only measurable quantities that are invariant to variable cloud cover, provided that polarized light is still
detectable below the clouds. It is shown that the sum of these 4 azimuths can be turned into a celestial
compass in a few short steps. A simulation shows that the compass is accurate as well as simple and well
suited for a robot or drone. It can also explain many of the experimental results published on insect
navigation.
1 INTRODUCTION
Due to the scattering of light within the earth’s
atmosphere, skylight is partially linearly polarized,
discovered by the Irish Scientist Tyndall (1869).
Two years later a mathematical description of the
phenomenon was given by Lord Rayleigh (1871) for
the scattering by small particles (air molecules) in
the atmosphere. That an insect can use this
polarization to navigate was first discovered in
experiments with bees by Karl von Frisch (1949).
It took another 25 years before the nature of the
insect’s celestial compass began to be clarified
(Kirshfeld et al., 1975; Bernard and Wehner, 1977).
It depends primarily on a specialized part of the
insect compound eye, a comparatively small group
of photoreceptors, typically 100 in number, situated
in the dorsal rim area. Further insight on these
photoreceptors came from Wehner and co-workers
working with desert ants and bees (Labhart, 1980;
Rossel and Wehner, 1982; Fent and Wehner, 1985;
Wehner, 1997). It was found that each ommatidium
in the dorsal rim of the compound eye has two
photoreceptors with axes of polarization at right
angles to one another and each strongly sensitive to
the E-vector orientation of plane polarized light. The
axes of polarization of these ommatidia have a fan
shaped orientation that has been claimed from
experiments to provide an approximate map for the
polarized sky, a map which the insect can use as a
compass (Rossel, 1993). The variation in E-vector
orientation has also been traced within the central
complex of the brain of an insect (Heinz and
Homberg, 2007).
Although much is known about this insect
compass little is known about the underlying
physical processes that require these 100
photoreceptors, the subject of this research. One
attempt has been made to design a navigational aid
for a robot based on the compass; this uses 3 pairs of
photoreceptors (Wehner, 1997; Lambrinos et al,
1998), simulating the accumulation of results from
many photoreceptors in three different parts of the
fan of receptors used by an insect. This system is
reported to work well in the desert but it is not clear
that it would be accurate under a variable cloudy
sky. NASA has also built robots navigating by
skylight, but these apparently use a different process
based on 3 photoreceptors with 3 different axes of
polarization on a horizontal plane (NASA, 2005).
Few details have been released publicly on this
system or its performance.
This paper proposes that the fan of
photoreceptors is scanning the sky to find the four
points in the sky where the polarization angle, χ, the
angle between the meridian and the polarized E-
vector in the sky, equals ±π/4. We propose that the
anatomy of the eyes of bees, ants, and many other
363
Smith F. (2009).
INSECT NAVIGATION BY POLARIZED LIGHT.
In Proceedings of the International Conference on Bio-inspired Systems and Signal Processing, pages 363-368
DOI: 10.5220/0001553503630368
Copyright
c
 SciTePress

insects are designed precisely to detect these four
points, probably the only measurable quantities
invariant to variable light cloud cover. We also show
that the direction of the sun can be found quickly by
a simple algorithm well within the capacity of the
insect brain for all orientations of the head.
In a previous work-in-progress paper (Smith,
2008) a simulation of this insect compass was
attempted using an algorithm involving 16 elements
in a 4X4 array in which all possible solar elevations
were examined one after the other until the correct
elevation was found. Probably this was too difficult
for the brain of an insect and in further studies of
previous experiments on insects it was found that
when insects view the sky through two different
windows they obtain solar azimuths equal to the
average of the two azimuths obtained from each
window (Wehner, 1997). This could not be
explained as part of the above algorithm. In addition
a mapping of the celestial compass in the insect
brain by Heinz and Homberg (2007), although it too
involved sets of arrays of 16 elements, indicated that
the processing of polarized light in the brain
involved simple pairing of contributions from
different sources. These facts led to the discovery of
a new much simpler algorithm in this paper and to a
better understanding of the invariance of the
algorithm to cloud conditions.
In the following we first summarise the
derivation of mathematical expressions for the light
intensities measured by the insect photoreceptors.
This is brief as more details are given in the previous
paper (Smith, 2008). We then show how these
intensities can give the direction of the sun in the
new algorithm
2 THEORY
2.1 Measured Intensities
In an ideal sky with no cloud, as shown by Rayleigh
(1871), the light observed from any patch of sky is
partially polarized, with an elliptical profile for the
electric vector, E, in which the major axis of the
ellipse is at right angles to both the direction of the
sun, represented by the unit vector, S, and to the
direction of the observed patch of sky, k’. The
electric vector in the direction of the major axis is
the E-vector. In the ideal situation where all of the
light observed is scattered once only, the ratio of E
in the directions of the minor axis to the major axis
is cos (θ) where θ is the scattering angle between S
and k’.
When this partially polarized light enters an
ommatidium in the dorsal rim its intensity is
measured by two photoreceptors, each of which can
measure polarized light with parallel structures
called microvilli. The two directions of the
microvilli are at right angles to one another, and
define two orthogonal axes of polarization for these
X and Y photoreceptors. In Figure 1 we illustrate the
orientations of the microvilli in the dorsal rim of the
honey bee by Sommer (1979), as redrawn by Rossel
(1993). The fan shape of the microvilli is apparent.
Figure 1: The paired orthogonal photoreceptors in the
dorsal rims of a bee. The axes of polarization of the Y
photoreceptors are dark, the X photoreceptors light.
The centres of the patches of sky being
observed by the photoreceptors are on the opposite
side of the head, i.e. contralateral (Sommer, 1979).
An examination of Figure (1) shows the axes of the
X photoreceptors are approximately parallel to the
meridians passing through these patches of sky
contralaterally. The same approximate parallel
pattern was found in desert ants by Wehner and
Raber (1979). It follows that the angle that the X
polarization axis makes with this meridian always
equals zero. The discovery that this angle is zero,
learned from the anatomy of bees and ants, turns out
to be critical, and it greatly simplifies the
expressions for the light intensities, S
X
and S
Y
,
measured by the two receptors, X and Y. But before
writing down these expressions we note that in the
real world the sky is not blue, but has a degree of
haze or cloud differing with direction. The light then
entering the ommatidia can be viewed as made up of
two components, one partly polarized as in
Rayleigh’s equations, and the second totally
BIOSIGNALS 2009 - International Conference on Bio-inspired Systems and Signal Processing
364

unpolarized due to multiple scattering. We let U be
the intensity of unpolarized light measured by both
photoreceptors. Then the 2 light intensities are:
[
]
UPS
X
+−= )(sin)(sin1
22
χθ
(1)
[
]
UPS
Y
+−= )(cos)(sin1
22
χθ
(2)
where the factor P depends on terms derived by
Rayleigh (1871) and on the measuring capability of
the photoreceptors.
It has been shown by Labhart (1988) that the
brain of a cricket records the difference between the
two signals, S
Y
and S
X
or rather the difference
between the log of the two signals; so the recorded
signal is
)/()()(
XYXYYX
SSLogSLogSLogS =−=
(3)
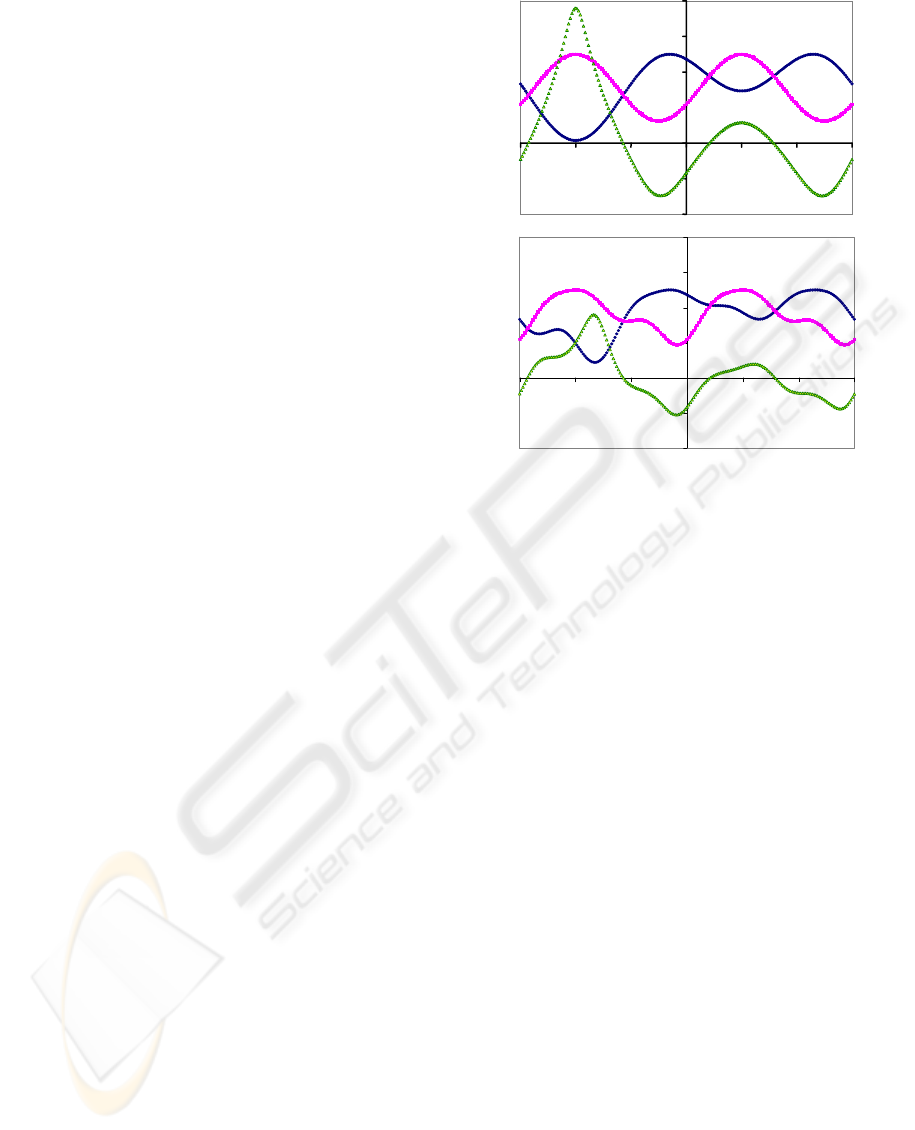
To illustrate the variation in these signals as the
azimuth angles of the ommatidia vary we set P = 1
and U=0 in the top of Figure (2). In the bottom we
include simulated clouds by putting U=0.5 sin
2
(a
o
)
with P=1-U. The curves change with cloud cover
but uniquely the zeros in S
YX
are always the same, as
evident mathematically by equating Equations (1)
and (2).
2.2 Solar Azimuth and Elevation
To proceed further we need the polarization angle, χ,
in terms of the solar azimuth, a
s
, and solar elevation,
h
s
. We need also the known azimuth, a
o
, and
elevation, h
o
, of the centre of the patch of sky being
observed by the photoreceptors.
We also know that the E-vector, in the direction
i’, is at right angles to the plane containing the solar
unit vector, S. So i’.S = 0. In our previous paper
(Smith, 2008) it is shown by substituting for S and i’
that this becomes:
0)cos()sin()sin(
)cos()cos()sin()cos()sin()cos()cos(
=−
−
s
ha
s
ha
o
h
s
h
o
h
χ
χχ
(4)
where a = a
s
– a
o
is the azimuth of the sun relative
to the azimuth of the observed sky. We use this
equation later.
2.3 A Compass for a Cloudy Sky
We need to know why insects are measuring the
difference S
YX
between the signals from the two
orthogonally polarized photoreceptors in each
ommatidium. First, the absolute value of the
difference S
YX
is between logs of intensities as in
Equation (3) and since this equals the log of the ratio
-0.8
-0.4
0
0.4
0.8
1.2
1.6
-180 -120 -60 0 60 120 180
Syx
Sy
Sx
Clouded Sky
ao
Figure 2: Illustration of the signals S
X
S
Y
and S
YX
in a
perfect blue sky [U=0] and a sky with simulated clouds
[U=0.5 sin
2
(ao)], as they vary with the azimuth, a
o
, of the
fan of observations measured from the central axis of the
insect with solar elevation h
s
=30
o
, and azimuth a
s
=60
o
.
Note that there are 4 azimuths a
o
where S
YX
=0 or Sx=Sy,
called zeros, and that these are unchanged by the cloud.
of S
T
to S
X
an examination of Equations (1) and (2)
shows that it reduces the effect of the unknown
unpolarized light intensity U caused by clouds, but it
does not remove it. So little reliable information can
be obtained from the absolute values of S
YX
. Instead,
the ommatidia are probably measuring the positions
of features in the measured intensities rather than the
values of the intensities. As these ommatidia scan
the sky through 360
o
S
YX
goes through a maximum
towards the solar meridian, then a minimum, then a
maximum towards the antisolar meridian and finally
a second minimum. Between these four extrema are
four directions in which S
YX
equals zero. So there are
two possibilities: that the ommatidia are looking for
the positions of the 4 extrema or for the positions of
the 4 zeros.
(a) 4 Extrema
As explained above the difference S
YX
in Equation
(3) goes through maxima in the directions of the
solar meridian, a
s
, and of the antisolar meridian,
a
s
+π. This is because the signal S
Y
goes through a
maximum in these directions while S
X
goes through
a minimum. So the difference between them
enhances the maximum in S
Y
Labhart (1988). If at
-0.8
-0.4
0
0.4
0.8
1.2
1.6
-180 -120 -60 0 60 120 180
ao
o
Blue Sky
Syx
Sy
Sx
INSECT NAVIGATION BY POLARIZED LIGHT
365

least one of these 2 maxima is found then it
immediately gives the direction of the sun or the
opposite direction. Other clues can then tell the
insect which of the two directions is correct.
The positions of the other 2 extrema, the 2
minima cannot be used so easily. Although the
minima of S
Y
occur at a
s
±π/2 the maxima in S
X
do
not, and may be as much as 20
o
different. This is
partly because in these directions the factor sin
2
(θ) in
Equations (1) and (2) is not stationary as it is in the
directions a
s
and a
s
+π. So the 2 minima in S
YX
cannot be used in the celestial compass
Although a maximum in S
YX
gives the positions
of the sun, the finding of the exact position of a
maximum, even enhanced, is not easy; so small
errors are likely. But a bigger problem comes from
cloud. As evident from Figure (2) variable cloud can
shift the position of a maximum or produce false
maxima, causing further errors. The wide window of
observation used by insects minimises this effect but
does not remove it. Simulations with a wide window
and real cloudy skies by Labhart (1999) have shown
that the errors caused by cloud in the positions of the
maxima were small, mostly 3
o
or less, but a few
larger errors occur. Nevertheless this approximate
position of the sun is a valuable check or an
alternative to what we now describe.
(b) 4 Zeros
The second possibility is that S
YX
is measuring the 4
zeros. Firstly zeros can be measured more accurately
than the positions of maxima, and secondly the
positions of zeros are almost completely unaltered
by variable cloud, provided only that there is some
polarized light detectable below the cloud. So the
two sources of errors in the positions of the maxima
are removed. We now show how we can use these 4
accurate measurements of zeros to calculate the
sun’s position.
Putting S
YX
= 0 or S
X
=S
Y
in Equations (1 to 3)
brings about a large simplification eliminating the
unknowns U, P and θ in one step and reduces the
equations to simply:
)(cos)(sin
22
χχ =
. This
makes χ = ±π/4. So finding the zeros where S
YX
=0
tells us the precise azimuths a
o
= Z where χ = ±π/4.
Examples of zeros for different solar elevations for a
constant window of observation between elevations
45
o
and 89
o
are shown in Figure (3). There are
almost always 4 zeros if the window of observation
is at a constant elevation. However, when the solar
elevation is high there may be no zeros. In this case
a robot or insect might increase the elevation of
observation (although this reduces the accuracy).
-90
90
-90 90
Sun
Figure 3: Projection of the sky showing for each solar
elevation the 4 azimuths relative to the sun, of zeros where
S
YX
= 0 and χ=±π/4. These zeros are invariant to cloud
cover. The circles represent elevations of 0
o
, 30
o
and 60
o
.
Therefore, noting that cos(χ) = 1 and sin(χ) = ±1 at
the zeros, Equation (4) simplifies to:
)tan()cos()sin(
)sin()cos(
soos
oos
hhaa
haa
=−±
−
(5)
Solving this for a
s
, the azimuth of the sun, gives
expressions for a
s
, for the 4 zeros where a
o
=Z:
δ
γ
±
±
=
Za
s
(6)
in which δ = arccos(tan(h
s
)cos(h
o
)/K) and γ =
arcsin(1/K) where K
2
= 1+ sin
2
(h
o
). If the robot
scans the sky at a constant elevation h
o
then the
angles γ and δ are also constant, simplifying the
algorithm (Smith, 2008). The angle γ depends only
on the elevation of the observation, it is large, >π/4,
and known to the insect or robot. The angle δ
depends on the solar elevation and when the sun is
on the horizon it equals π/2. It can be calculated by a
robot from the above equation for δ, which needs the
solar elevation, known from the latitude and time;
fortunately we now show that this difficult
calculation is not needed by an insect.
The 4 alternatives in Equation (6) correspond to
the four zeros as illustrated in Figure (4), which we
write as
a
s
= Z
1
+ γ – δ, a
s
= Z
2
– γ – δ (7)
a
s
= Z
3
– γ + δ, a
s
= Z
4
+ γ+ δ (8)
where the signs are chosen by symmetry in the
geometry in Figure (4). Note that all of these
quantities are angles in [0,2π]; so the sums are all
modulus 2π.
If we sum these 4 expressions the γ and δ terms
cancel and we get 4a
s
= Z
1
+Z
2
+Z
3
+Z
4
, mod 2π.
Dividing by 4 gives a
s
, but because of the cyclic
nature of the summation (350
o
+ 20
o
= 10
o
) an
uncertainty of mπ/2 occurs where m=0, 1, 2 or 3.
BIOSIGNALS 2009 - International Conference on Bio-inspired Systems and Signal Processing
366

This uncertainty can be resolved by noting in Figure
4 that (1) Z
2
– Z
1
= Z
4
– Z
3
and (2) the two zeros Z
1
and Z
4
nearest to the sun are closer together than the
other two. These two conditions are used in the
following algorithm to calculate a
s
from 4 measured
zeros, Y
1
, Y
2
, Y
3
, and Y
4
, where at first the order is
not known, i.e. which one of them is Z
1
in Figure 4.
So the algorithm is simple:
1. find the 4 zeros in [0, 2π] where S
X
= S
Y
;
2. put in order Y
1
, Y
2
, Y
3
, and Y
4
;
3. find the sum: S = Y
1
+ Y
2
,+ Y
3
+ Y
4
;
4. put i=1; m=0;
5. if y
2
– y
1
<> y
4
– y
3
then i=2 and m=1;
6. if y
i
– y
i+3
< y
i+2
– y
i+1
then m=m+2;
7. a
s
= (S/4 + m*π/2) mod 2π.
(Note that differences are cyclical and clockwise.)
For example, for a solar elevation h
s
= 60
o
and
observation elevation h
o
= 70
o
we find 4 zeros at 84
o
,
120
o
, 213
o
, and 351
o
. Following the algorithm we
find that m=3 and the 4
th
one is Z
1
, S=768
o
,
S/4=192
o
and a
s
=192
o
+270
o
=462
o
=102
o
, the correct
solar azimuth. Simulations with about 5000
examples have shown that this algorithm succeeds in
almost every case with no ambiguity within a
tolerance of 1 degree. Errors occur only at low or
high solar elevations ( ≤ 2
o
or > h
o
), as long as four
zeros are found.
2.4 Less than 4 Zeros
If 4 zeros cannot be found because part of the
observed sky is obscured a robot can use the average
of the detectable zeros, along with the known values
of γ and δ, to calculate the solar azimuth. Other
clues, such as light intensity, are needed for the signs
of the corrections, remembering that the corrections
are large. An insect, not being able to calculate δ,
puts δ=π/2, assuming that the sun is on the horizon
(Rossel & Wehner, 1982), and uses the average of
the available values: z ± γ ± π/2. Since γ is known
this leaves an error of ±(δ-π/2) if one zero only is
observed. If 2 zeros are observed then the average of
the two zeros gives an error of ±(δ-π/2) or, if they
are symmetric about the solar meridian, an error of
zero. Calculated values of these errors are in general
agreement with experiments with insects (Wehner,
1989). This supports our proposal that the insect
compass is based primarily on the 4 zeros.
An insect may use only two zeros based on the
equations: 2a
s
= Z
1
+Z
4
and 2a
s
= Z
2
+Z
3
deduced
from Equations (7) and (8). We were lead to this
pairing of zeros and to our algorithm by structures
Z1
Z2Z3
Z4
Sun
Figure 4: Example of the approximate azimuths
(directions) of the 4 zeros where S
YX
= 0 relative to the
direction of the sun for a solar elevation h
s
= 60
o
.
found within the brain of an insect observing
polarized light by Heinz & Homberg (2007).
2.5 Robot Design
For a robot the greatest difficulty in building our
skylight compass is finding the direction of the four
zeros. One design (mimicking an insect) uses about
100 pairs of photoreceptors in a circle round the
robot. A problem is that each pair has to observe a
patch of sky with an accurate azimuth and elevation.
In another design the robot has one pair of
photoreceptors which is rotated through 360
o
(like
radar) measuring the azimuth as it moves at a
constant high elevation (e.g. 70
o
). This single pair of
photoreceptors can be made highly sensitive to small
differences in polarization. This would be made
easier by the use of ultraviolet light which can
penetrate cloud more easily than visible light; it is
the light used by most insects (Pomozi et al., 2001).
Although an insect views the polarized sky
contralaterally (for reasons that are unclear) it is
more straight forward for the robot to scan the sky
ipsilaterally, but with the orientations of the
polarization axes in the same directions as an insect.
3 CONCLUSIONS
We have shown that an accurate celestial compass
for a robot can be built round the principle of finding
in skylight the 4 zeros at a constant elevation. The
algorithm was discovered after studying published
experiments on insect navigation and anatomy. The
algorithm is simple and accurate and well within the
capacity of the insect brain. It also allows an insect
to navigate continuously without turning its head. It
explains many experiments on insect behaviour.
Besides the simplicity and accuracy of the
method its greatest advantage is that it is accurate in
INSECT NAVIGATION BY POLARIZED LIGHT
367

hazy and partially clouded skies, because the
position of the zeros is unchanged by cloud. No
other method shows this invariance.
However, much remains uncertain about insect
navigation. For the algorithm to be accurate the top
of the robot or drone must be pointing towards the
zenith. Insects may do this using the 3 ocelli on the
top of their heads (Goodman, 1970). But how they
would do this is not clear. Many insects also have
ommatidia in sets of three with the polarization axes
of the 3 sets differing by about π/3 (Labhart, 1988;
Wehner, 2001). There are several possibilities. If 3
ommatidia from different sets point at the same
patch of sky they could be used to calculate the
polarization angles χ, even in a cloudy sky.
Alternatively they might help identify in one of them
the signs of the corrections ±γ and ±δ if less than 4
zeros are visible. Yet another possibility is that they
are looking also for the 4 zeros where χ = ±π/4 + π/3
and the 4 zeros where χ = ±π/4 - π/3. The algorithm
above might then be repeated for each of the 3 sets
of zeros, giving 3 different approximations for the
solar azimuth. All these possibilities are being
investigated.
REFERENCES
Bernard, G D, Wehner, R, 1977. Functional similarities
between polarization vision and color vision, Vision
Res., 17, 1019-28.
Fent, K, Wehner, R, 1985. Ocelli: A celestial compass in
the desert ant Cataglyphis, Science, 228, 192-4.
Goodman, L. J., 1970. The structure and function of the
insect dorsal ocellus. Adv. Insect Phys., 7, 97-195.
Heinze, S, Homberg, U, 2007. Maplike Representation of
Celestial E-Vector Orientations in the Brain of an
Insect, Science, 315, 995-7.
Kirschfeld, K, Lindauer, M, Martin,H, 1975. Problems in
menotactic orientation according to the polarized light
of the sky, Z. Naturforsch, 30C, 88-90.
Labhart, T, 1980. Specialized Photoreceptors at the dorsal
rim of the honeybee’s compound eye: Polarizational
and Angular Sensitivity, J Comp. Phys., 141, 19-30.
Labhart, T, 1988. Polarized-opponent interneurons in the
insect visual system, Nature, 331, 435-7.
Labhart, T, 1999. How polarization-sensitive
interneurones of crickets see the polarization pattern of
the sky: a field study with an optoelectronic model
neurone, J. Exp. Biol., 202, 757-70.
Lambrinos, D, Maris, M, Kobayashi, H, Labhart, T,
Pfeifer, P, Wehner, R, 1998. Navigation with a
polarized light compass, Self-Learning Robots II: Bio-
Robotics (Digest 1998/248) IEE, London, 7/1-4.
NASA, 2005. www.nasatech.com/Briefs/Oct05/ NPO_41
269.html
Pomozi, I, Horvath, G, Wehner, R., 2001. How the clear-
sky angle of polarization pattern continues underneath
clouds, J. Expt. Biol, 204, 2933-42.
Rayleigh, Lord, 1871. On the light from the sky, its
polarisation and colour, Phil Mag,, 41, 107-20, 274-9.
Rossel, S, 1993. Mini Review: Navigation by bees using
polarized skylight, Comp. Biochem. Physiol, 104A,
695-705.
Rossel, S, and Wehner, R, 1982. The bee’s map of the e-
vector pattern in the sky, Proc. Natl. Acad. Sci. USA,
79, 4451-5.
Sommer, E W, 1979. Untersuchungen zur topo-
graphischen Anatomie der Retina und zur
Sehfeldoptologie im Auge der Honigbiene, Apis
mellifera (Hymenoptera). PhD Thesis, Un. Zurich.
Smith, F J, 2008. A new algorithm for navigation by
skylight based on insect vision, in Biosignals 2008, 2,
Eds. P Encarnacao & A Veloso, Madeira, 185-90.
Tyndall, J, 1869. On the blue colour of the sky, the
polarisation of skylight, and on the polarisation of
cloudy matter, Proc. Roy. Soc., 17, 223.
Von Frisch, K, 1949. Die Polarization des Himmelslichts
als Orientierender Faktor bei den Tanzen der Bienen,
Experientia, 5, 142-8.
Wehner, R, 1989. The hymenopteran skylight compass:
matched filtering and parallel coding, J Exp. Biol.,
146, 63-85.
Wehner, R, 1997. The Ant’s celestial compass system:
spectral and polarization channels, In Orientation and
Communication in Arthropods, Ed. M. Lehler,
Birkhauser, Berlag, Basel, Switzerland, 145-85.
Wehner, R, and Raber, F, 1979. Visual spatial memory in
desert ants, Cataglyphis bicolor (Hymenoptera:
Formicidae), Experientia, 35, 1569-71.
Wehner, R, 2001. Polarization vision – a uniform sesory
capacity, J. Exp. Biol., 204, 2589-96.
BIOSIGNALS 2009 - International Conference on Bio-inspired Systems and Signal Processing
368