CLASSIFICATION OF MASS SPECTROMETRY DATA

Using Manifold and Supervised Distance Metric Learning

Qingzhong Liu

a,b

, Andrew H. Sung

a,b

, Bernardete M. Ribeiro

c,*

and Mengyu Qiao

Department of Computer Science,

Institute for Complex Additive Systems Analysis

New Mexico Tech, Socorro, NM 87801, U.S.A.

Department of Informatics Engineering, University of Coimbra, Portugal

Keywords: Proteomics, Mass spectrometry, Manifold, Distance metric learning, Classification, Support vector machine.

Abstract: Mass spectrometry becomes the most widely used measurement in proteomics research. The quality of the

feature set and applied learning classifier determine the reliability of the prediction of disease status. A well-

known approach is to combine peak detection and support vector machine recursive feature elimination

(SVMRFE). To compare the feature selection and to search for alternative learning classifier, in this paper,

we employ a distance metric learning to classification of proteomics mass spectrometry (MS) data.

Experimental results show that distance metric learning is promising for the classification of proteomics

data; the results are comparable to the best results by applying SVM to the SVMRFE feature sets. Results

also indicate that the good potential of manifold learning for feature reduction in MS data analysis.

1 INTRODUCTION

Mass spectrometry (MS), which includes a sequence

of the ratios of mass/charge (m/z), is currently used

for biomedical diagnosis and protein identification

(Petricoin and Liotta, 2003). The data mining

usually contains four steps, or pre-processing,

feature extraction, feature selection and

classification.

The objective of pre-processing is to purify the

data, and systematically represent the data for the

following steps. Generally speaking, MS data

contain two kinds of noise, electric noise and

chemical noise, which damage the classification

result. The chemical noise, usually shows as a

baseline along the spectrum, is generated by matrix

or ion overloading. Baseline correction computes the

local minimum value and draws a baseline

representing as the background noise and subtracts

the baseline from the spectrum. Williams et al

proposed a robust algorithm for computing the

baseline correction of MALDI-MS spectra

(Williams et al., 2005). The electronic noise, usually

randomly distributed in the spectra, is produced

from the electronic instrument. To remove the noise,

Chen et al designed a wavelet-based denoising

(Chen et al., 2007). The denoised data are

normalized to provide a systematic representation of

the spectra.

The next steps include extracting features from

the spectra, and forming the initial complete feature

set. The simplest way is to obtain every data point as

a discriminative feature, and finally have a huge

feature set including more than 15000 features (Li et

al., 2007), (Li et al., 2002), that is stupid for

classification. Recently, some researchers employed

an elaborated algorithm for peak detection and

performed a more aggressive feature extraction

(Coombes et al., 2007), (Hilario et al., 2006), (Shin

and Markey, 2006). A popular method to deal with

the feature selection in MS data classification is to

apply support vector machine recursive feature

elimination (SVMRFE) for getting a small subset of

peaks as input variables for the classification (Guyon

et al., 2002), (Vapnik, 1998), (Liu et al., 2008),

followed by SVM for the final testing.

To search for promising alternative classifiers

and to feature dimensionality reduction, in this

paper, we apply a distance metric learning, called

large margin nearest neighbor classifier (LMNN)

that is proposed by Weinberger (Weinberger et al.,

2006), to the classification of MS data. We also

compare the testing results on the reduced feature

sets with the use of a manifold learning.

Experimental results show that distance metric

learning is promising for the classification of

proteomics data; the results are comparable to the

best results by applying SVM to the SVMRFE

396

Liu Q., H. Sung A., M. Ribeiro B. and Qiao M. (2009).

CLASSIFICATION OF MASS SPECTROMETRY DATA - Using Manifold and Supervised Distance Metric Learning .

In Proceedings of the International Conference on Bio-inspired Systems and Signal Processing, pages 396-401

DOI: 10.5220/0001556403960401

 SciTePress

feature sets. Results also indicate that the good

potential of manifold learning for feature reduction

in MS data analysis.

The remainder is organized as follows. Pre-

processing algorithms are briefly discussed in

section two, LMNN is introduced in section three

and experimental results are given in section four,

followed by our conclusions in section five.

2 PREPROCESSING DATA

MS data have high dimensionality and small number

of samples. Both chemical and electrical noises are

involved in the signal. The redundancy of the

spectra, different reference points, and unaligned

feature points increase the computational intensity

and decrease the classification accuracy. To deal

with these issues, the proposed processing

procedures include spectra re-sampling, wavelet de-

noising, baseline correction, normalization, peak

detection and alignment.

2.1 Spectra Re-sampling and Wavelet

De-noising

The mass spectrum data is in a discrete format and

the intervals are not equal in the whole spectrum.

For high-resolution data, the high-frequent noise and

redundant data points harm the quality of the dataset.

So, we have to set the common low-frequent mass

value to every sample spectrum in order to give a

unified representation. By using spline interpolation,

we resample the data and confine the interval to a

unified size. Before re-sampling, the sample

spectrum has a little variation from the true

spectrum. The data is re-sampled to a standard

discrete data which could be analyzed in frequency

domain. The electrical noise is generated during the

mass spectrum acquisition by the instrument and it is

almost random distributed noise. The next step is to

employ discrete wavelet transform for eliminating

the electrical noise. By applying a wavelet

transform, the original signal is decomposed into

multi-level wavelet coefficients. By setting up a

threshold value, given percentiles of lower value

coefficients are removed. Then, we apply

polynomial filter of second order to smooth the

signal and get better data quality.

2.2 Baseline Correction and

Normalization

To minimize the chemical noise, the baseline should

be subtracted from the spectrum. In order to obtain

the baseline, the local minima should be computed

by assigning an appropriate window size. Then, we

use spline interpolation to fit the baseline. In order to

compare sample spectra, we need to normalize the

data to represent the data in a systematic scale.

2.3 Peak Detection and Qualification

The final feature acquisition of MS data is to obtain

the peak position and its magnitude. In our mass

spectrum experiment, the peak detection method

proposed by Coombes et al (Coombes et al, 2005) is

performed on mean spectrum rather than individual

spectra, and we used the ad hoc method based on

signal to noise ratio to select the large peaks

(Coombes et al., 2007).

3 DISTANCE METRIC

LEARNING

Distance metric learning includes supervised

learning and unsupervised learning.

For unsupervised distance metric learning or

called manifold learning, the main idea is to learn an

underlying low-dimensional manifold where

geometric relationship between most of the observed

data are preserved. Every dimension reduction

approach is essentially to learn a distance metric

without label information. Manifold learning

algorithms can be divided into global linear

dimension reduction approaches, including Principle

Component Analysis (PCA) and Multiple

Dimension Scaling (MDS), global nonlinear

approaches, for instance, ISOMAP (Tenenbaum et

al., 2000), local linear approaches, including Locally

Linear Embedding (LLE) (Saul and Roweis, 2003)

and the Laplacian Eigenmap (Belkin and Niyogi,

2003). Here we introduce a locally linear embedding

proposed in Roweis and Lawrance, 2000) that is a

local method to establish the mapping relationship

between the observed data and the corresponding

low-dimensional data and to preserve local order

relation of data in both the embedding space and the

intrinsic space, described as follows:

1. Find the n nearest neighbor for each x

the dataset. By assuming that each data

point and its neighbors lie on a locally

linear patch of the manifold, the local

geometry of these patches can be

characterized by linear coefficients that

reconstruct each data point from its

neighbors. The reconstruction error can be

measured by

CLASSIFICATION OF MASS SPECTROMETRY DATA - Using Manifold and Supervised Distance Metric Learning

397

(W) || W ||

iijij

=−

∑

(1)

2. Construct the approximation matrix by

minimizing

|| W ||

iijij

−

∑∑

(2)

s.b.

∑

3. Construct a neighbor-preserving mapping.

The idea is that the reconstruction weights

reflect intrinsic geometric properties of the

data and are invariant to the linear

transform from a high dimensional

coordinates of each neighborhood to global

internal coordinates on a low dimensional

manifold. The details are given in Roweis

and Lawrance, 2000).

Supervised distance metric learning can be

divided into global distance metric learning and

local distance metric learning. The global learns the

distance metric in a global sense, i.e., to satisfy all

the pairwise constraints. The local approach seeks

only to meet local pairwise constraints.

In supervised global distance metric learning, the

representative work is to formulate distance metric

learning as a constrained convex programming

problem (Xing et al., 2003). It learns a global metric

distance that minimizes the distance between the

data pairs in the equivalence constraints subject to

the constraint that the data pairs in the inequivalence

constraints are well separated. In local adaptive

distance metric learning, many researchers presented

approaches to learn appropriate distance metric to

improve KNN classifier (Domeniconi and

Gunopulos, 2002), (Peng et al., 2002), (Goldberger

et al., 2005), (Zhang et al., 2003), (Zhang et al.,

2005).

Inspired by the work on neighborhood

component analysis (Goldberger et al., 2005) and

metric learning by energy-based models (Chopra et

al., 2005), Weinberger et al. proposed a distance

metric learning for Large Margin Nearest Neighbor

classification (LMNN). Specifically, the

Mahanalobis distance is optimized with the goal that

k-nearest neighbors always belong to the same class

while examples from different classes are separated

by a large margin (Weinberger et al., 2006). LMNN

has several parallels to learning in support vector

machines (SVMs), for example, the goal of margin

maximization and a convex objective function based

on the hinge loss. In multi-classification, the training

time of SVMs scales at least linearly in the number

of classes, by contrast, LMNN has no explicit

dependence on the number of classes (Weinberger et

al., 2006). We introduce the idea of LMNN as

follows:

Given a training set of n labeled samples and the

corresponding class labels

{}

, the binary

matrix

{0,1}

y ∈

indicates whether or not the

labels

and

match. And

{0,1}

∈

indicates

whether

is a target neighbor of

. Both matrices

and

are fixed during training. The goal is to

learn a linear transformation

L: R R

→

that

optimizes KNN classification. The transform is used

to compute squared distance as

D(,)||L(,)||

ij ij

xx xx=

(3)

The cost function is given as follows:

(L) L( )

(1 ) 1 L ( ) L( )

ij i j

ij jl i j i l

ijl

Cy xxxx

εη

=−

⎡

⎤

+−+−−−

⎢

⎥

⎣

⎦

∑

(4)

Where [z]

= max(z,0) denotes the standard

hinge loss and the constant C > 0. The first term

penalizes large distances between each input and its

target neighbors and the second term penalizes small

distances between each input and all other inputs

that do not share the same label.

The optimization of eq. (2) can be reformulated

as an instance of semidefinite programming (SDP)

Vandenberghe and Boyd, 1996) and the global

minimum of eq. (2) can be efficiently computed.

Mahalanobis distance metric

MLL

= , then eq. (1)

D( , ) ( ) M( )

ij i j i j

xxx xx=− −

(5)

Slack variables

for all pairs of differently

labeled inputs are introduced so that the hinge loss

can be mimicked. The resulting SDP is given by:

Minimize

(L) ( ) ( ) (1 )

ij i j i j ij jl ijl

ij ijl

xxMxx C y

ηηξ

=− −+ −

∑

Subject to

(1)

()M()( )M( )1

il il i j i j ijl

xx xx xx xx

−

−−− − ≥−

(2)

ijl

≥

(3)

M0≥

BIOSIGNALS 2009 - International Conference on Bio-inspired Systems and Signal Processing

398

4 MATERIALS AND

EXPERIMENTS

4.1 Dataset

The following two mass spectrometry datasets have

been tested in our experiment.

1. High resolution time-of-flight (TOF) mass

spectrometry (MS) proteomics data set from surface-

enhanced laser/desorption ionization (SELDI)

ProteinChip arrays on 121 ovarian cancer cases and

95 controls. The data sources can be accessed by

FDA-NCI Clinical Proteomics at

http://home.ccr.cancer.gov/ncifdaproteomics/ppatt

erns.asp

2. The breast cancer QC SELDI spectra data set

was studied by Pusztai et al. (Pusztai et al., 2004).

Here we utilized data of 57 controls and 51 cases.

The data set may be downloaded at:

http://bioinformatics.mdanderson.org/Supplemen

ts/Datasets

We process the dataset according to the methods

described in section 2 for peak detection. And then

apply LMNN to the detected peak spectra data.

Since SVMRFE is a classical feature selection based

on the weights of the support vectors (Guyon et al.,

2002) and is widely used in the classification of

proteomics data with the use of SVM, we also

compare the results by using LMNN with Euclidean

distance, Mahalanobis distance, and energy-based

classification (Weinberger et al., 2006) and SVM

combining with SVMRFE on the detected peak data.

In each experiment, 80% samples are randomly

chosen for training and the remaining 20% samples

are tested. We repeated the experiments 10 - 100

times and compared the average testing results.

Besides applying SVMRFE to the features

chosen by peak-detection algorithm, we also apply

the manifold learning to the features chosen by

peak-detection and the features filtered by rank-sum

test without peak-detection, and obtain the reduced

features that are mapped from high-dimension to

low-dimension, then we apply a support vector

machine and KNN to the reduced feature sets and

compare the testing results.

4.2 Experiments on Peak Detection

with SVMRFE

Figure 1 list the average testing accuracy values by

applying SVM to SVMRFE on ovarian cancer data

set and breast cancer data set, respectively. These

data sets were preprocessed with the use of peak-

detection algorithms before the use of SVMRFE.

(a) Ovarian cancer (b) Breast cancer

Figure 1: The testing accuracy by applying SVM to the

feature sets with the use of SVMRFE on ovarian cancer

data set (a) and breast cancer data set (b).

Table 1 lists the average testing accuracy by

applying LMNN classifiers to the peak data sets.

Table 2 lists the best averaging testing accuracy by

applying SVM to the feature sets chosen by

SVMRFE from the peak data sets.

Table 1: Average testing accuracy with LMNN classifiers.

Data set Classifier

Testing

accuracy

Ovarian

cancer

LMNN_energy

99.3%

LMNN_Euclidean 84.6%

LMNN_Mahalanobis 99.0%

Breast

cancer

LMNN_energy 81.8%

LMNN_Euclidean 84.6%

LMNN_Mahalanobis 81.7%

Table 2: The best average testing accuracy by applying

SVM to feature sets ranked by SVMRFE.

Data set Testing accuracy

Ovarian cancer 98.0%

Breast cancer

89.5%

Comparing the results listed in tables 1 and 2, we

can see that, although the testing results in table 1

are not as good as the best result by applying SVM

to SVMRFE feature sets for breast cancer data set,

the results by applying LMNN classifiers based on

energy classification and Mahalanobis distance are

both better than the best result obtained by applying

SVM to SVMRFE feature sets. It indicates that

LMNN classifiers with energy classification and

Mahalanobis metric are competitive for the

classification of proteomics data, especially

considering that the best testing accuracy by

applying SVM to SVMRFE feature sets after we

tested each dimensionality from 1 to 200 for ovarian

cancer data set and tested each dimensionality from

1 to 150 for breast cancer data set. Furthermore,

normally we cannot accurately predict the best

CLASSIFICATION OF MASS SPECTROMETRY DATA - Using Manifold and Supervised Distance Metric Learning

399

testing results that correspond to which

dimensionality.

We also test the classification results by applying

LMNN to the feature sets chosen by SVMRFE, and

compare the best testing result and the least number

of the features corresponding to the best result in

each experiment against the results with the use of

SVM, shown in table 3. Experimental results

indicate comparable results by applying LMNN and

support vector machines.

Table 3: The highest testing accuracy and the least number

of the features corresponding to the highest testing results.

Data

set

Classifier

Testing

accuracy

Feature

number

Ovaria

cancer

LMNN_energy

99.5%

LMNN_Euclidean 98.4% 10

LMNN_Mahalanobis

99.5%

SVM 99.3% 11

Breast

cancer

LMNN_energy 92.6% 27

LMNN_Euclidean 90% 28

LMNN_Mahalanobis 92.5% 25

SVM

94%

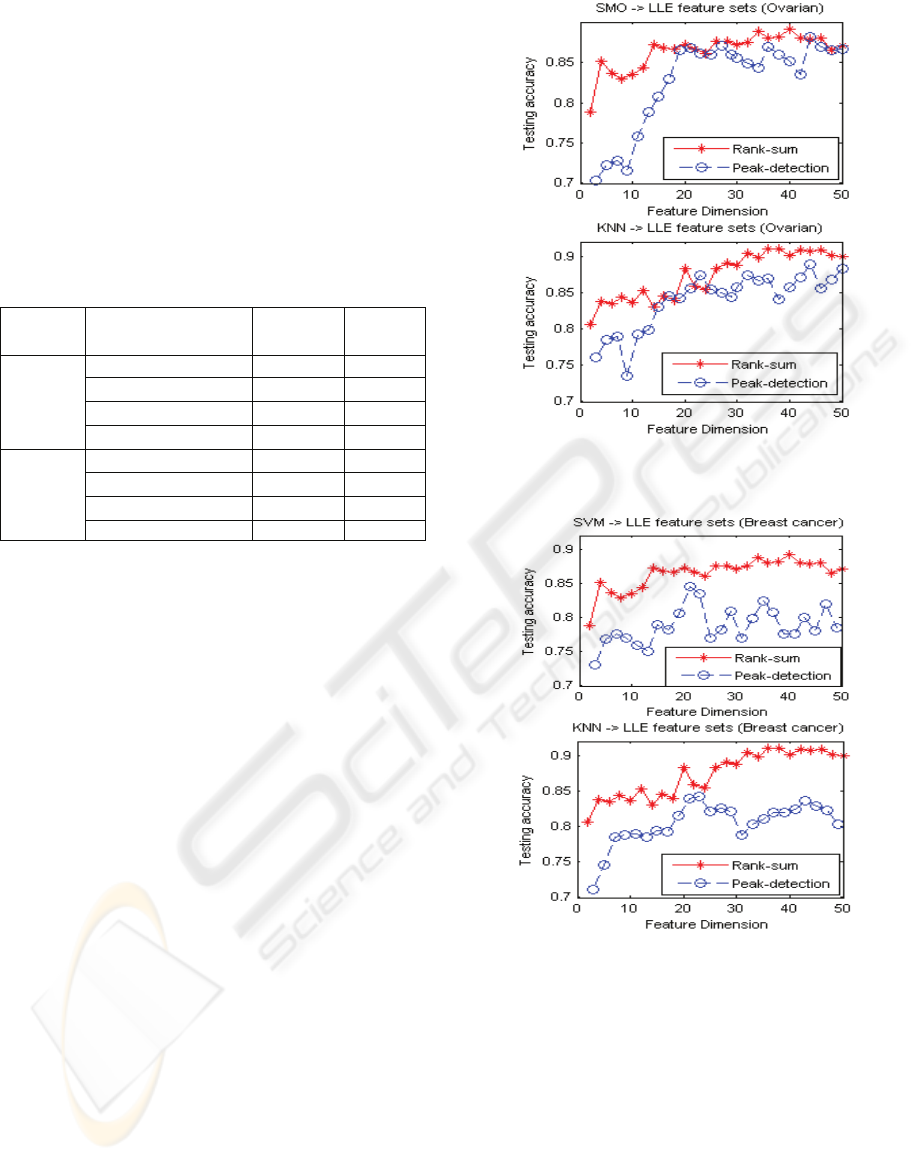
4.3 Manifold for Feature Reduction

We also preprocess the data sets by using peak-

detection algorithms (method one) and filtered the

data sets by using rank sum test without peak-

detection (method two), then we apply the manifold

learning Roweis and Lawrance, 2000) to reduce the

features, finally we employ a SVM and a KNN to

classify the data sets. Figure 2 gives the comparison

of the testing accuracy of these two methods, with

and without peak-detection on the ovarian cancer

data. Figure 3 plots the testing results on breast

cancer data.

Figures 2 and 3 indicate that the testing results

on the reduced feature sets preprocessed from rank

sum test are better than the results on the reduced

feature sets preprocessed by peak detection. It seems

to imply that peak detection cannot include all useful

features. This is worthy of further study.

We also note that the testing results on ovarian

data set are not better than the results obtained by

using SVMRFE, shown in 4.2. However, the results

on breast cancer are comparable to the results with

the use of SVMRFE, given in section 4.2. It

indicates that unsupervised metric learning or

manifold learning holds good promise in dealing

with high-feature dimension data for dimension

reduction and this makes interesting future study.

Figure 2: The testing results of the LLE reduce feature sets

on peak-detection and rank sum test, ovarian cancer data.

Figure 3: The testing results of the LLE reduce feature sets

on peak-detection and rank sum test, breast cancer data.

5 CONCLUSIONS

In this paper, we compared a supervised distance

metric learning, large margin nearest neighbor

classifier and SVM for classification of mass

spectrometry proteomics data. Experiments

produced good results of applying distance metric

learning to proteomics data, comparable to the

results by applying SVM. Our results also indicate

the potential of manifold learning in feature

BIOSIGNALS 2009 - International Conference on Bio-inspired Systems and Signal Processing

400

reduction. Further, our results also indicate that,

peak detection may not be the optimal choice for

pre-processing proteomics data.

ACKNOWLEDGEMENTS

Support for this research received from the Institute

of Complex Additive Systems Analysis, a unit of

New Mexico Tech, is gratefully acknowledged.

REFERENCES

Petricoin, E. and Liotta, L. (2003), Mass spectrometry-

based diagnostic: the upcoming revolution in disease

detection. Clin. Chem., 49, pp.533-534.

Williams, B., Cornett, S., Dawant, B., Crecelius, A.,

Bodenheimer, B. and Caprioli, R. (2005), An

algorithm for baseline correction of MALDI mass

spectra, Proceedings of the 43rd annual Southeast

regional conference, March 18-20, 2005, Kennesaw,

Georgia.

Chen, S., Hong, D. and Shyr, Y. (2007), Wavelet-based

procedures for proteomic mass spectrometry data

processing, Computational Statistics & Data Analysis,

2007, Vol. 52, issue 1, pp.211-220.

Li, L. et al. (2004), Applications of the GA/KNN method

to SELDI proteomics data. Bioinformatics, 20,

pp.1638-1640.

Petricoin, E. et al. (2002), Use of proteomics patterns in

serum to identify ovarian cancer. The Lancet, 359,

pp.572-577.

Coombes, K. et al. (2007), Pre-processing mass

spectrometry data. In Dubitzky, M., et al. (eds.),

Fundamentals of Data Mining in Genomics and

Proteomics. Kluwer, Boston, pp.79-99.

Hilario, M. et al. (2006), Processing and classification of

protein mass spectra. Mass Spectrom. Rev., 25:409-

449.

Shin, H. and Markey, M. (2006), A machine learning

perspective on the development of clinical decision

support systems utilizing mass spectra of blood

samples. J. Biomed. Inform. 39, pp.227-248.

Furey, T. et al. (2000), Support vector machine

classification and validation of cancer tissue samples

using microarray expression data. Bioinformatics, 16:

906-914.

Coombes, K. et al. (2005), Improved peak detection and

quantification of mass spectrometry data acquired

from surface-enhanced laser desorption and ionization

by denoising spectra with the undecimated discrete

wavelet transform, Proteomics, Volume 5, Issue 16.

Duan, K. and Rajapakse, J.C. (2004), SVM-RFE peak

selection for cancer classification with mass

spectrometry data. APBC 2005: pp.191-200.

Guyon, I., Weston, J., Barnhill, S. and Vapnik, V.N.

(2002), Gene Selection for Cancer Classification using

Support Vector Machines. Machine Learning. 2002

46(1-3): pp.389-422.

Vapnik,V.N. (1998), Statistical Learning Theory. John

Wiley and Sons, New York.

Brown, M.P.S. et al. (2000), Knowledge-based analysis of

microarray gene expression data by using support

vector machines. Pro. Nat Acad. Sci., 97, pp.262-267.

Liu, Q., Sung, A.H., Chen, Z. and Xu, J. (2008), Feature

Mining and Pattern Classification for Steganalysis of

LSB Matching Steganography in Grayscale Images,

Pattern Recognition, 41(1): pp.56-66.

Tenenbaum, J., Silva, V. de and Langford, J. C. (2000), A

global geometric framework for nonlinear

dimensionality reduction, Science, vol. 290, pp.2319-

2323.

Saul, L. K. and Roweis, S. T. (2003), Think globally, fit

locally: Unsupervised learning of low dimensional

manifolds, Journal of Machine Learning Research,

vol. 4, pp.119-155.

Belkin, M. and Niyogi, P. (2003), Laplacian eigenmaps

for dimensionality reduction and data representation,

Neural Computation, 15( 6):1373-1396.

Xing, E., Ng, A., Jordan, M., and Russell, S. (2003),

Distance metric learning with application to clustering

with side-information, in Proc. NIPS, 2003.

Domeniconi, C. and Gunopulos, D. (2002), Adaptive

nearest neighbor classification using support vector

machines, Proc. NIPS, 2002.

Peng, J., Heisterkamp, D. and Dai, H. (2002), Adaptive

kernel metric nearest neighbor classification, Proc.

International Conference on Pattern Recognition,

2002.

Goldberger, J., Roweis, S., Hinton, G. and Salakhutdinov,

R. (2005), Neighbourhood components analysis, in

Proc. NIPS, 2005.

Zhang, Z., Kwok, J. and Yeung, D. (2003), Parametric

distance metric learning with label information, in

Proc. International Joint Conference on Artificial

Intelligence, 2003.

Zhang, K., Tang, M. and Kwok, J. T. (2005), Applying

neighborhood consistency for fast clustering and

kernel density estimation. in Proc. Computer Vision

and Pattern Recognition, 2005, pp. 1001-1007

Chopra, S., Hadsell, R. and. LeCun Y. (2005), Learning a

Similarity Metric Discriminatively, with Application

to Face Verification, Proc. Computer Vision and

Pattern Recognition, 2005, Vol. 1, pp.539-546.

Weinberger, K., Blitzer, J. and Saul, L. (2006), Distance

metric learning for large margin nearest neighbor

classification, in Proc. NIPS, 2006, pp.1475-1482.

Pusztai et al. (2004), Pharmacoproteomic Analysis of

Prechemotherapy and Postchemotherapy Plasma

Samples from Patients Receiving Neoadjuvant or

Adjuvant Chemotherapy for Breast Carcinoma,

Cancer 100: pp.1814-1822.

Vandenberghe, L. and Boyd, S.P. (1996), Semidefinite

programming, SIAM Review, 38(1): 49-95.

Roweis, S. T. and Lawrance, K. S. (2000), Nonlinear

dimensionality reduction by locally linear embedding,

in Science, vol. 290, 2000, pp.2323-2326.

CLASSIFICATION OF MASS SPECTROMETRY DATA - Using Manifold and Supervised Distance Metric Learning

401