PROJECTOR CALIBRATION USING A MARKERLESS PLANE

Jamil Drar

eni, S

ebastien Roy

DIRO, Universite de Montreal , CP 6128 succ Centre-Ville, Montreal QC, Canada

Peter Sturm

INRIA Rhone-Alpes , 655 Avenue de lEurope, 38330 Montbonnot St Martin, France

Keywords:

Video projector calibration, Planar calibration, Focal estimation, Structured light, Photometric stereo.

Abstract:

In this paper we address the problem of geometric video projector calibration using a markerless planar surface

(wall) and a partially calibrated camera. Instead of using control points to infer the camera-wall orientation,

we ﬁnd such relation by efﬁciently sampling the hemisphere of possible orientations. This process is so fast

that even the focal of the camera can be estimated during the sampling process. Hence, physical grids and full

knowledge of camera parameters are no longer necessary to calibrate a video projector.

1 INTRODUCTION

With the recent advances in projection display, video

projectors (VP) are becoming the devices of choice

for active reconstruction systems. Such systems like

Structured Light (Salvi et al., 2004) and Photometric

Stereo (Woodham, 1978; Barsky and Petrou, 2003)

use VP to alleviate the difﬁcult task of establishing

point correspondences. However, even if active sys-

tems can solve the matching problem, calibrated VP

are still required. In fact, a calibrated projector is

required to triangulate points in a camera-projector

structured light system, or to estimate the projector’s

orientation when the latter is used as an illuminant de-

vice for a photometric stereo system.

Since a video projector is often modeled as an in-

verse camera, it is natural to calibrate it as part of a

structured light system rather than as a stand alone

device. In order to simplify the calibration process, a

planar surface is often used as a projection surface on

which features or codiﬁed patterns are projected. The

projector can be calibrated as a regular camera, ex-

cept for the fact that a regular accessory camera must

be used to see the projector patterns. The way pat-

terns are codiﬁed and the projection surface orienta-

tion is estimated will distinguish the various calibra-

tion methods from each other.

In (Shen and Meng, 2002), a VP projects patterns

on a plane mounted on a mechanically controlled plat-

form. Thus, the orientation and position of the projec-

tion plane is known and is used to calibrate the struc-

tured light system using conventional camera calibra-

tion techniques.

Other approaches use a calibrated camera and a

planar calibration chessboard attached to the projec-

tion surface (Ouellet et al., 2008; Sadlo et al., 2005).

For convenience and because the projection sur-

face is usually planar, we will refer to it as the wall.

The attached chessboard is used to infer the orienta-

tion and the position of the wall w.r.t the camera. This

relation is then exploited, along with the images of the

projected patterns to estimate the intrinsic parameters

of the projector.

In order to measure the 3D position of the pro-

jected features, (Sadlo et al., 2005) estimates the ho-

mography between the attached chessboard and the

camera. This allows the computation of the extrin-

sic parameters of the camera. It is important to men-

tion that the camera must be fully calibrated in this

case. With at least three different orientations, a set

of 3D-2D correspondences can be obtained and then

used to estimate the VP parameters with standard

plane-based calibration methods (Sturm and May-

bank, 1999; Zhang, 1999). We refer to this method

as Direct Linear Calibration (DLC). To increase accu-

racy of the DLC, a printed planar target with circular

markers is used in (Ouellet et al., 2008), to calibrate

the camera as well as the projector.

In (Lee et al., 2004), a structured light system is

calibrated without using a camera. This is made pos-

377

DrarÃl’ni J., Roy S. and Sturm P.

PROJECTOR CALIBRATION USING A MARKERLESS PLANE.

DOI: 10.5220/0001559603770382

In Proceedings of the Fourth International Conference on Computer Vision Theory and Applications (VISIGRAPP 2009), page

ISBN: 978-989-8111-69-2

sible by embedding light sensors in the target surface.

Gray-coded binary patterns are then projected to es-

timate the sensor locations and prewarp the image to

accurately ﬁt the physical features of the projection

surface. The VP parameters are not explicitly esti-

mated but the method could easily be extended for

that purpose.

In this paper, a new projector calibration method

is introduced. The proposed method does not require

a physical calibration board nor a full knowledge of

the camera parameters.

We overcome the problem of determining the

camera-wall homography H

w→c

by exploring the

space of all acceptable homographies and consider

the one that minimizes the reprojection error (see

Figure.1). Since H

w→c

depends only on the orienta-

tion between the camera and the wall, the space of

acceptable homographies can be parameterized with

only 2 angles: the elevation and the azimuth angles

that deﬁne the normal vector at the wall.

Figure 1: The homography wall-camera is deﬁned by the

orientation of the wall.

Finding the normal of the wall consists then in

sampling the space of orientations on a unit sphere.

For each orientation sample, a DLC is performed and

we select the homography that minimizes the repro-

jection errors in the images. It is worth mentioning

that our DLC implementation differs slightly from the

one used in (Sadlo et al., 2005) as explained in the

next section.

Our proposed method is fully automatic, fast and

produces excellent results as shown in our experi-

ments. We also show that when the camera is not fully

calibrated, projector calibration is still tractable. This

is done by making the common assumptions that the

pixels are square and that the center of projection co-

incides with the image center (Snavely et al., 2006).

Thus, the only unknown camera parameter left to es-

timate is the focal length, which is estimated by sam-

pling.

The rest of this paper is organized as follows. Sec-

tion 3 presents our variant of the direct linear cali-

bration for a projector. Section 4 details our orien-

tation sampling calibration (OSC) using only a (par-

tially calibrated) camera and a marker-less projection

plane.

Section 5 presents the results of our calibration

method, followed by a discussion of limitations and

future work in Section 6.

2 VIDEO PROJECTOR MODEL

We model the video projector as an inverse camera.

Therefore, we intend to compute the intrinsic and ex-

trinsic parameters. Without loss of generality, we con-

sider in this paper a 4 parameters projector model,

namely: the focal length, the aspect ratio and the prin-

cipal point. Thus, the projector matrix K

is deﬁned

as:





ρ f 0 cx

0 f cy

0 0 1





The extrinsic parameters that describe the i

pro-

jector pose are the usual rotation matrix R

and the

translation vector t

3 DIRECT LINEAR

CALIBRATION

In this section, we review the details of the Direct Lin-

ear Calibration for projectors. This method is used

as a reference for our benchmark test. As opposed

to (Sadlo et al., 2005), the variant presented here is

strictly based on homographies and does not require a

calibrated camera.

VISAPP 2009 - International Conference on Computer Vision Theory and Applications

378

If a static camera observes a planar surface (or a

wall), a homography is induced between the latter and

the camera image plane. This linear mapping (H

w→c

)

relates a point P

on the wall to a point P

in the cam-

era image as follows:

∼ H

w→c

· P

(1)

Where ∼ denotes equality up to a scale. Details

on homography estimation can be found in (Hartley

and Zisserman, 2004).

The video projector is used afterward to project

patterns while it is moved to various positions and

orientations. For a given projector pose i, correspon-

dences are established between the camera and the

VP, leading to a homography H

c→ p

. A point P

the image i is mapped into the projector as:

∼ H

c→ p

· P

(2)

Combining Eq.1 an Eq.2, a point P

on the wall is

mapped into the i

projector as:

∼ H

c→ p

· H

w→c

| {z }

w→ p

·P

(3)

On the other hand, P

and P

are related through

a perspective projection as:

∼ K





· P

(4)

Where K

, R

1,2

and t

are respectively the projec-

tor intrinsic parameters, the two ﬁrst vectors of the ro-

tation matrix R

, and the translation vector. From Eq.3

and Eq.4, a relation between H

w→ p

and the extrinsic

parameters of the projector is derived as follows:

−1

· H

w→ p

∼





(5)

With at least two different orientations, one can

solve for K

−1

by exploiting the orthonormal prop-

erty of the rotation matrix as explained in (Sturm and

Maybank, 1999).

4 ORIENTATION SAMPLING

CALIBRATION

In this section we give the details of our proposed

video projector calibration method. As discussed ear-

lier, the justiﬁcation for using an attached calibration

rig to the wall is to infer the homography wall-camera

in order to estimate the 3D coordinates of the pro-

jected features. We propose to estimate this wall-

camera relation by exploring the space of all possible

orientations since only the orientation of the wall w.r.t

the camera matters and not its position.

Another way to look at this orientation space is to

consider all vectors lying on a unit hemisphere placed

on the wall, as depicted on Figure 1.

The calibration process can be outlined in three

main steps:

• Pick a direction on the hemisphere.

• Compute the corresponding homography.

• Use the homography to perform a DLC calibra-

tion (Section 3).

The above steps are repeated for all possible di-

rections and the direction that minimizes the reprojec-

tion errors is selected as the correct plane orientation.

The ﬁrst two steps are detailed in the next subsections.

The third one is straightforward from section 3.

4.1 Sampling a Hemisphere

The problem of exploring the set of possible orienta-

tions is dependent on the problem of generating uni-

formly distributed samples on the unit sphere (hemi-

sphere in our case).

Uniform sphere sampling strategies can be ran-

dom or deterministic (Yershova and LaValle, 2004).

The ﬁrst class are based on random parameters gen-

eration, followed by an acceptance/rejection step de-

pending on whether the sample is or not on the

sphere. Deterministic methods produce valid samples

on a unit sphere from uniformly distributed parame-

ters, such method include (but not limited to) quater-

nion sampling (Horn, 1986), normal-deviate methods

(Knuth, 1997) and methods based on Archimedes the-

orem (Min-Zhi Shao, 1996). We chose to use the lat-

ter method for its simplicity and efﬁciency. As the

name suggests, this method is based on Archimedes

theorem on the sphere and cylinder which states that

the area of a sphere equals the area of every right

circular cylinder circumscribed about the sphere ex-

cluding the bases. This argument leads naturally to

a simple sphere sampling algorithm based on cylin-

der sampling (Min-Zhi Shao, 1996). Uniformly sam-

pling a cylinder can be done by uniformly choosing

an orientation θ

∈ [0,π] (we call it azimuth) to obtain

a directed vector d(θ

,0) (See Figure.2). After that,

a height h

is uniformly chosen in the range [−1,1].

The resulting vector, noted d

(θ

), is axially pro-

jected on the unit sphere. According to the above the-

orem, if a point is uniformly chosen on a cylinder, its

inverse axial projection will be uniformly distributed

on the sphere as well, see (Min-Zhi Shao, 1996) for

further details.

In our case, we only need to sample the hemi-

sphere facing the camera. Thus the span of the

PROJECTOR CALIBRATION USING A MARKERLESS PLANE

379

Figure 2: Orientation space sampling.

points that must be visited is limited to the range

[−1,+1]× [0,π].

4.2 Homography From an Orientation

Sample

The homography wall-camera H

w→c

induced by a

wall whose normal is a direction d

(as deﬁned in the

previous subsection), is deﬁned by:

w→c

∼ K

cam





(6)

Where K

cam

, R

and t are respectively the in-

trinsic camera matrix, the ﬁrst two vectors of the ro-

tation corresponding to the direction d

, and the trans-

lation vector. Without loss of generality and for the

sake of simplicity, we ﬁx the projection of the origin

of the wall P

= (0,0)

into the camera at the image

center. With this convention, the translation vector t

simpliﬁes to (0,0,1)

The rotation matrix R

is computed via Rodrigues

formula, which requires a rotation axis and a rota-

tion angle. The rotation axis is simply the result of

the cross product between d

and the vector (0,0,1)

whereas the rotation angle α

is obtained from the dot

product of the same vectors:

= cos

−1



· (0,0,1)



(7)

4.3 Complete Algorithm

We are now ready to give the complete algorithm

of our video projector calibration. We assume the

existence of two supporting functions, ReprojError

that returns a reprojection error for a given projector

parameters and DLC a function that estimate the

projector parameters using the DLC method (see

Section.3).

Algorithm 1: Orientation Sampling Calibra-

tion.

Data: H

c→ p

, the k camera-projector

homographies and K

cam

Camera intrinsic

matrix (optional).

foreach (h

,θ

)∈[−1,1]×[−π/2,π/2] do

Estimate direction d

(θ

) (sec.4.1)

if K

cam

is undef then

Initialize elements of K

cam

using image

center and f

end

Estimate H

w→c

from d

and f

(sec.4.2)

foreach H

c→ p

w→ p

= H

c→ p

· H

w→c

end

pro j

← DLC(H

c→ p

) (sec.3)

Error ← ReprojError(K

pro j

)

if Error < BestError then

pro j

← K

pro j

BestError ← Error

end

return Projector calibration matrix K

pro j

5 EXPERIMENTS

We have evaluated the proposed calibration method

with both a calibrated and an uncalibrated cam-

eras. The results were also compared to the DLC

method. The evaluation platform consists of a Mit-

subishi pocket projector of 800 × 600 pixels resolu-

tion and a digital camera (Nikon D50). A 50mm lens

was used on the camera and the resolution was set

to 1500 × 1000. The calibration of the camera using

the Matlab toolbox gave the following intrinsic matrix

cam





3176.3115 0 790.6186

0 3172.4809 495.3829

0 0 1





To include the DLC algorithm in our benchmark,

the camera was mounted on a tripod and was ﬁrst reg-

istered to the wall using an attached printed chess-

board. Images of projected chessboard using the

video projector under several orientations were then

acquired using the camera. We took precaution to re-

move the attached chessboard form the wall before

acquiring the projector images to avoid overlaps be-

tween the projected patterns and the rigidly attached

pattern.

VISAPP 2009 - International Conference on Computer Vision Theory and Applications

380

Some images of the projected chessboard along

with detected features are depicted on Figure.3.

Figure 3: Images of projected patterns and detected fea-

tures. The numbers and small red dots are added for illus-

tration only. The large dots in the 4 corners are part of the

projected pattern.

Notice the presence of colored dots on the chess-

board. Those were used to compute a rough esti-

mate of the homography (which will be reﬁned) and

to eliminate the orientation ambiguity of the chess-

board while assigning 3D coordinates to the detected

features.

Our benchmark includes a projector calibration

using the DLC method, the proposed method with

both a calibrated and an uncalibrated camera. In the

ﬁrst case, we used the image of the attached checker

to infer the wall-camera homography and calibrated

as explained in Section.3. For the second method,

we used a multi-resolution strategy to sample the az-

imuth angles and heights. The conditions of the third

method were identical to the second one except that

the camera parameters were ignored and were esti-

mated as follows:

• The focal length estimation was included in the

sampling process. The sampling range was

[0,10000].

• The pixels are assumed square.

• The center of projection is assumed to coincides

with the image center.

The result of this benchmark is outlined on the Ta-

ble.1. The table provides the estimated parameters,

Table 1: Projector calibration benchmark: Direct method,

Orientation sampling with a calibrated camera (Sampling-

C) and Orientation sampling with an uncalibrated camera

(Sampling-U).

Method f

proj

ρ cx cy estf

cam

Error Error B.A

Direct 1320.13 1.02 382.1 368 - 4.35 0.47

Sampling-C 1327.30 1.01 377.4 366 - 0.43 0.22

Sampling-U 1322.15 1.00 376 360 3108 0.16 0.09

the reprojection errors in pixels (Error), and the er-

ror difference comparing before and after applying a

bundle adjustment reﬁnement (Error B.A). Technical

and implementation details on the latter can be found

in (Lourakis and Argyros, 2004).

The running times for a data set of 20 images on

an 1.5 Ghz computer are provided in Table.2.

Table 2: Execution time for Direct method, Sampling with

calibrated camera, and Sampling with uncalibrated camera.

Method Time (seconds)

Direct 0.18

Sampling-C 1.23

Sampling-U 6.2

From this test, we can see that our method, even

in the absence of camera parameters knowledge, out-

perform the Direct Linear Method at the expenses of a

higher running time. However, we are convinced that

the performance of our implementation could be fur-

ther improved by choosing a better multi-scale sam-

pling strategy. We also consider that not requiring a

printed chessboard attached to the wall is a major ad-

vantage, especially when the wall surface is large or

unaccessible.

A plot of the reprojection error in terms of the ori-

entation parameters h and α is provided in Figure.4.

We can clearly see that the function is very well be-

haved and easy to minimize.

As a last test, we wanted to assess the stability of

the focal length estimate. We thus ﬁxed the value of

the wall orientation at the value obtained in the ﬁrst

experiment and varied the focal length. The plot of

the reprojection error as a function of the sampled fo-

cal length of the camera is shown on Figure.5. As we

can see the error function is smooth and convex, sug-

gesting that the lack of knowledge of the focal length

can easily be circumvented in practice.

6 CONCLUSIONS

In this paper we presented a new video projector

calibration method. Contrary to most methods, we

showed that a physical target attached to a projection

surface is not necessary to achieve an accurate projec-

tor calibration. We also suggest that full knowledge

of camera parameters is not strictly required and can

PROJECTOR CALIBRATION USING A MARKERLESS PLANE

381

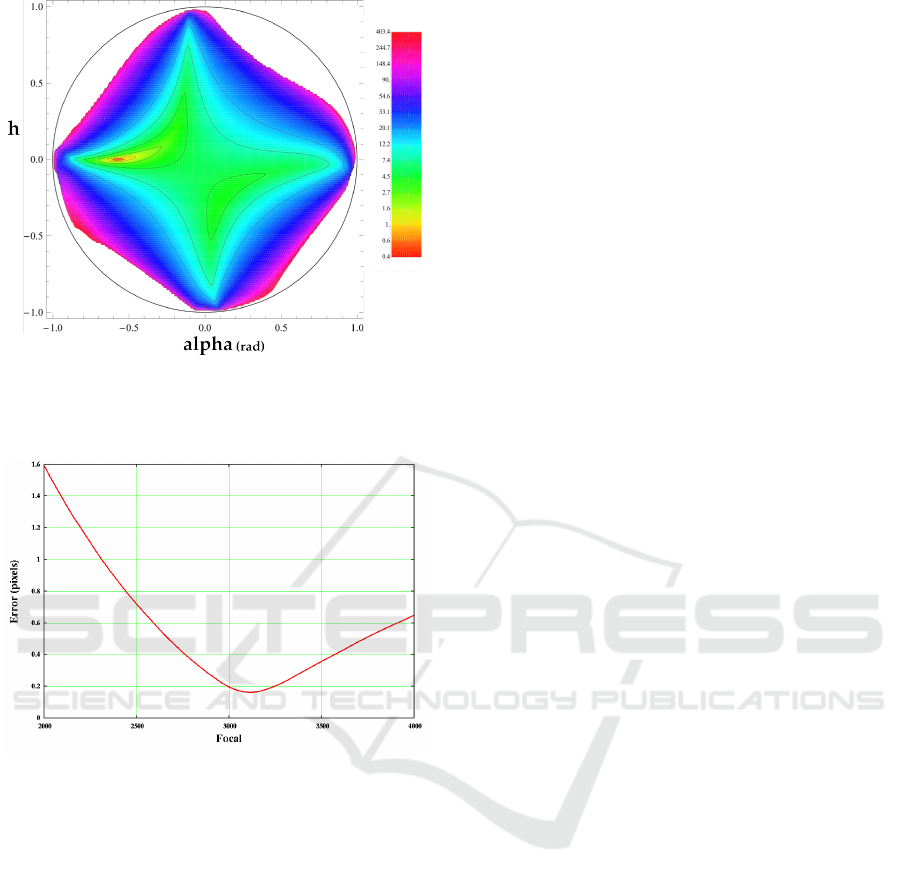
Figure 4: Reprojection error in terms of the orientation pa-

rameters h and α. The error computation does not include

bundle adjustment reﬁnement.

Figure 5: Reprojection error in terms of the camera focal

length values (prior to bundle adjustment procedure). The

minimum is reached at 3034.4, the off-line camera calibra-

tion estimated a camera focal of 3176.

be relaxed into a set of commonly used assumptions

regarding the camera geometry. Very simple to im-

plement, the proposed method is fast and will handle

large projector-camera systems that were previously

impossible to calibrate due to the impractical chess-

board.

REFERENCES

Barsky, S. and Petrou, M. (2003). The 4-source photomet-

ric stereo technique for three-dimensional surfaces in

the presence of highlights and shadows. IEEE Trans-

actions on Pattern Analysis and Machine Intelligence,

25(10):1239–1252.

Hartley, R. I. and Zisserman, A. (2004). Multiple View Ge-

ometry in Computer Vision. Cambridge University

Press, ISBN: 0521540518, second edition.

Horn, B. K. P. (1986). Robot Vision (MIT Electrical Engi-

neering and Computer Science). The MIT Press, mit

press ed edition.

Knuth, D. E. (1997). Art of Computer Programming,

Volume 2: Seminumerical Algorithms (3rd Edition).

Addison-Wesley Professional.

Lee, J. C., Dietz, P. H., Maynes-Aminzade, D., Raskar, R.,

and Hudson, S. E. (2004). Automatic projector cali-

bration with embedded light sensors. In Proceedings

of the 17th annual ACM symposium on User interface

software and technology, pages 123–126. ACM.

Lourakis, M. and Argyros, A. (2004). The de-

sign and implementation of a generic sparse

bundle adjustment software package based on

the levenberg-marquardt algorithm. Technical

Report 340, Institute of Computer Science -

FORTH, Heraklion, Crete, Greece. Available from

http://www.ics.forth.gr/˜lourakis/sba.

Min-Zhi Shao, N. B. (1996). Spherical sampling by

archimedes’ theorem. Technical Report 184, Univer-

sity of Pennsylvania.

Ouellet, J.-N., Rochette, F., and H

ebert, P. (2008). Geo-

metric calibration of a structured light system using

circular control points. In 3D Data Processing, Visu-

alization and Transmission, pages 183–190.

Sadlo, F., Weyrich, T., Peikert, R., and Gross, M. (2005). A

practical structured light acquisition system for point-

based geometry and texture. In Proceedings of the

Eurographics Symposium on Point-Based Graphics,

pages 89–98.

Salvi, J., Pag

es, J., and Batlle, J. (2004). Pattern codiﬁ-

cation strategies in structured light systems. Pattern

Recognition, 37(4):827–849.

Shen, T. and Meng, C. (2002). Digital projector calibration

for 3-d active vision systems. Journal of Manufactur-

ing Science and Engineering, 124(1):126–134.

Snavely, N., Seitz, S. M., and Szeliski, R. (2006). Photo

tourism: Exploring photo collections in 3d. In

SIGGRAPH Conference Proceedings, pages 835–846,

New York, NY, USA. ACM Press.

Sturm, P. and Maybank, S. (1999). On plane-based cam-

era calibration: A general algorithm, singularities, ap-

plications. In Proceedings of the IEEE Conference

on Computer Vision and Pattern Recognition, Fort

Collins, USA, pages 432–437.

Woodham, R. J. (1978). Photometric Stereo: A Reﬂectance

Map Technique for Determining Surface Orientation

from a Single View. In Proceedings of the 22

SPIE

Annual Technical Symposium, volume 155, pages

136–143, San Diego, California, USA.

Yershova, A. and LaValle, S. M. (2004). Deterministic sam-

pling methods for spheres and so(3). In ICRA, pages

3974–3980.

Zhang, Z. (1999). Flexible camera calibration by viewing

a plane from unknown orientations. Computer Vision,

1999. The Proceedings of the Seventh IEEE Interna-

tional Conference on, 1:666–673 vol.1.

VISAPP 2009 - International Conference on Computer Vision Theory and Applications

382