SPECIFYING MULTIAGENT ENVIRONMENTS IN THE GAME

DESCRIPTION LANGUAGE

Stephan Schiffel and Michael Thielscher

Department of Computer Science, Dresden University of Technology, 01062 Dresden, Germany

Keywords:

Knowledge Representation, Multiagent Systems, Game Playing.

Abstract:

The Game Description Language (GDL) has been developed for the purpose of formalizing game rules. It

serves as the input language for general game players, which are systems that learn to play previously un-

known games without human intervention. In this paper, we show that GDL can be readily used as a spec-

iﬁcation language for a large class of multiagent environments. The resulting speciﬁcations are declarative,

compact, and easy to understand and maintain. At the same time they can be fully automatically understood

and used by autonomous agents who intend to participate in these environments. Our main result is a formal

characterization of the class of multiagent environments that can be described in GDL.

1 INTRODUCTION

A novel and challenging research problem for Artiﬁ-

cial Intelligence, General Game Playing is concerned

with the development of systems that learn to play a

previously unknown game solely on the basis of the

rules. The Game Description Language (GDL) (Love

et al., 2006) has been developed to formalize the rules

of any ﬁnite, information-symmetric n-player game

in such a way that the description can be automati-

cally processed by a general game player (Genesereth

et al., 2006). As a declarative language, GDL sup-

ports speciﬁcations that are modular and easy to de-

velop, understand, and maintain. While the basic se-

mantics for GDL is grounded in standard logic, the

language uses several pre-deﬁned predicates as key-

words, whose intended meaning is only informally

described in (Love et al., 2006).

In this paper, we show that GDL can be readily

used as a speciﬁcation language for a large class of

multiagent environments. This allows for formalizing

the physics and laws that govern an arbitrary domain

in such a way that agents can automatically under-

stand the rules and thus know how to participate in

this environment. There is a variety of potential appli-

cations for machine processable descriptions of mul-

tiagent environments: the rules of an e-marketplace

can be made accessible to agents, the interface of in-

teractive Internet platforms for software agents can

be formally described, and agent competitions can be

run without revealing detailed problem speciﬁcations

in advance. In each of these cases, an autonomous

agent—or a team of agents—can learn how to partic-

ipate in a new or modiﬁed environment without the

need to be (re-)programmed for each speciﬁc case.

Because GDL uses a decidable subset of logic pro-

gramming, autonomous agents require just a simple,

standard reasoning module to be able to understand

and effectively process a given set of rules. Moreover,

if an agent environment is speciﬁed in GDL, success-

ful general game playing systems such as (Kuhlmann

et al., 2006; Clune, 2007; Schiffel and Thielscher,

2007; Finnsson and Bj¨ornsson, 2008) can be read-

ily employed as intelligent agents for these environ-

ments.

The main result in this paper is the deﬁnition of a

formal class of multiagent environmentswhich can be

expressed in GDL and, conversely, which can be used

to provide a semantics for any GDL game description.

As a by-product we thus obtain a formal semantics for

the special, pre-deﬁned keywords in GDL.

The rest of the paper is organized as follows. In

Section 2, we formally deﬁne the class of determin-

istic, synchronous multiagent environments. In Sec-

tion 3, we show how these can be axiomatically de-

scribed in GDL, and in the section that follows, we

present the converse result by showing how all GDL

games can be interpreted as a deterministic, asyn-

chronous multiagent environment. We conclude in

Section 5.

Schiffel S. and Thielscher M. (2009).

SPECIFYING MULTIAGENT ENVIRONMENTS IN THE GAME DESCRIPTION LANGUAGE.

In Proceedings of the International Conference on Agents and Artiﬁcial Intelligence, pages 21-28

DOI: 10.5220/0001560200210028

 SciTePress

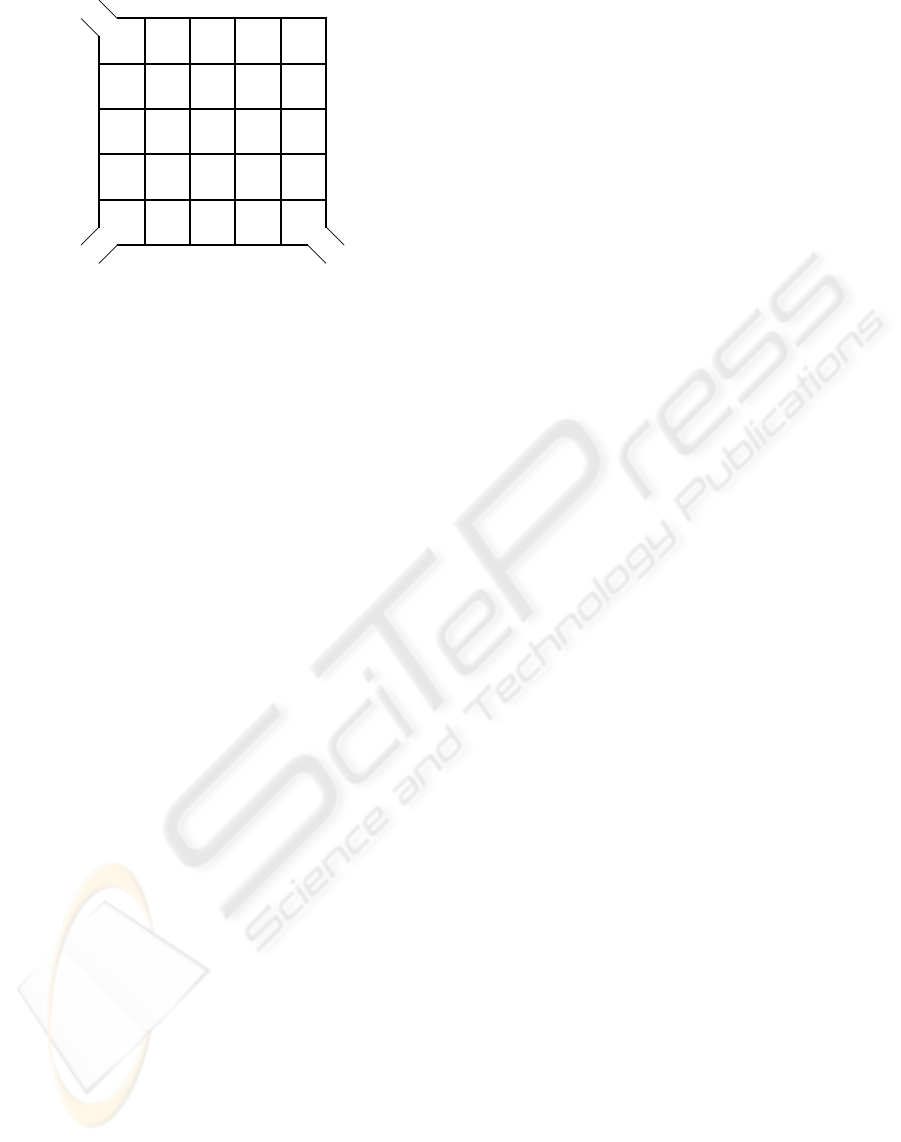
Figure 1: A simple multiagent domain: two “guard” agents

and Ag

shall cooperatively try to catch Ag

, whose

goal in turn is to escape via one of the three exits at lo-

cations (1,1), (5,1), and (1,5). All agents act syn-

chronously and can move horizontally or vertically to an

adjacent position. Ag

is caught when it ends up in the

same location as Ag

or Ag

, or when it crosses path with

one of them in a simultaneous move.

2 MULTIAGENT

ENVIRONMENTS

As the running examplein this paper, we will consider

the multiagent domain depicted in Figure 1. As a dis-

crete environment it can be formally described as a

ﬁnite state transition system. However, even though it

is obviously just a toy-size example, it has a consider-

ably large state space, rendering an explicit encoding

difﬁcult—and practically impossible for even slightly

larger environments. Fortunately it is possible to ex-

ploit the fact that any natural and realistic multiagent

environment has an internal structure, which allows

one to describe its dynamics with the help of symbols

that represent individual components. Our example

domain, for instance, can be formally described using

the following symbolic expressions: Ag

,Ag

representing the three agents; At(r,x, y), where r ∈

{Ag

,Ag

} and x,y ∈ {1, . . . , 5}, representing

the position of each agent; and Move(d), where

d ∈ {North,South,East, West}, along with Stay and

Exit, representing the possible actions.

Based on a suitable collection of symbols, multia-

gent domains can be formally described as follows.

Deﬁnition 1 Let Σ be a countable set of ground

(i.e., variable-free) symbolic expressions. A (discrete,

synchronous, deterministic) multiagent environment

is a structure

(R,s

,t,l,u, g)

where

• R ⊆ Σ ﬁnite (the agents, or roles);

• s

⊆ Σ ﬁnite (the initial state);

• t ⊆ 2

(the terminal states);

• l ⊆ R×Σ×2

(the action preconditions, or legal-

ity relation);

• u : (R 7→ Σ)× 2

7→ 2

(the transition function, or

update function);

• g ⊆ R× N × 2

(the utility, or goal relation).

Here, 2

denotes the set of all ﬁnite subsets of Σ, and

for any r ∈ R and S ∈ 2

, l(r,a,S) holds for ﬁnitely

many a ∈ Σ. 

This deﬁnition deserves some explanation. For the

sake of simplicity, the symbolic expressions are not

categorized—there is no formal distinction between

symbols for objects, state components, actions, etc.

For practical purposes, it is important that states are

ﬁnitely representable; hence, while possibly inﬁnitely

many symbols give rise to inﬁnitely many states, a

state itself is an element of the set of all ﬁnite subsets

of the given symbols. The legality relation l(r, a, S)

deﬁnes a to be a legal action for agent r in state S.

Again for the sake of practical usability, it is assumed

that every agent in every state has only ﬁnitely many

possible actions. The update function takes an ac-

tion for each agent and (synchronously) applies the

joint actions to a current state, resulting in the updated

state. For the sake of simplicity, we take natural num-

bers n ∈ N as the utility of a state S for agent r in

the goal relation g(r, n,S).

For illustration, consider a formalization of the

multiagent environment of Figure 1 using the sym-

bols introduced above.

• R = {Ag

,Ag

};

• s

= {At(Ag

,1,1), At(Ag

,5,1), At(Ag

,5,5)} ;

• t contains all states

{At(Ag

),At(Ag

)}

(that is, where Ag

has escaped) along with all

states

{At(Ag

),At(Ag

)}

in which x

= x

∧ y

= y

or x

= x

∧ y

= y

(that is, where Ag

has been caught);

• l is deﬁned as follows: each agent can always

Stay; in every non-terminal state each agent can

Move(d) in any direction d unless this would

lead outside the physical environment; Ag

can

Exit from any of the locations (1,1), (5,1),

or (1, 5), provided it has not been caught.

• u is deﬁned as follows: actions Stay, Exit, and

Move(d) have the expected effects on the indi-

vidual locations of the agents, with the exception

ICAART 2009 - International Conference on Agents and Artificial Intelligence

that when the paths of Ag

and either of Ag

(or both) cross in a simultaneous move, then

ends up (caught) in the same location as Ag

or Ag

, respectively. For illegal actions or states

that are not reachable, u may be arbitrarily de-

ﬁned.

• g shall be deﬁned as true for n = 100 and r =

in terminal states in which this agent has es-

caped; conversely, g holds for n = 100 and both

and Ag

in terminal states in which Ag

got

caught. In all other states the goal relation gives

value 0 for all three agents.

We have thus obtained a formal, symbolic descrip-

tion of the example multiagent environment. How-

ever, this speciﬁcation is not yet amenable to auto-

matic processing by an autonomous agent, because it

uses natural language to describe some of the compo-

nents. If this were to be translated into an explicit enu-

meration of the transition function, this would again

yield too large a description to be of any practical use.

In the following section, we show how the Game De-

scription Language can be readily used to provide a

fully axiomatic, compact description of arbitrary mul-

tiagent environments; a description that on the one

hand is declarative and easy to understand and main-

tain by humans, and on the other hand can be fully au-

tomatically processed by artiﬁcial, autonomous agent

systems.

3 AXIOMATIZING MULTIAGENT

ENVIRONMENTS AS GAME

DESCRIPTIONS

The Game Description Language (GDL) has been

developed to formalize the rules of any ﬁnite game

with complete information in such a way that the de-

scription can be automatically processed by a general

game player. In this section, we ﬁrst recapitulate the

GDL syntax from (Love et al., 2006) and then show

how the multiagent environments deﬁned in the pre-

ceding section can be formally described in this lan-

guage.

3.1 General GDL Syntax

GDL is based on the standard syntax of logic pro-

grams, including negation. A logic program is a set

of clauses according to the following deﬁnition (see,

e.g., (Lloyd, 1987)).

Deﬁnition 2

• A term is either a variable, or a function sym-

bol applied to terms as arguments (a constant is

a function symbol with no argument);

• An atom is a predicate symbol applied to terms as

arguments;

• A literal is an atom or its negation;

• A clause is an implication h ⇐ b

∧.. . ∧b

where

head h is an atom and body b

∧ . . . ∧ b

a con-

junction of literals (n ≥ 0).



We adopt the Prolog convention according to which

variables are denoted by uppercase letters and predi-

cate and function symbols start with a lowercase let-

ter. (The interested reader may take a peek at Figure 2

at this point to see some example clauses, which in

fact constitute a complete GDL axiomatization of our

running example domain.) GDL imposes some gen-

eral restrictions on a set of clauses, with the intention

to ensure ﬁnite derivability.

Deﬁnition 3 The dependency graph for a set G

of clauses is a directed, labeled graph whose nodes

are the predicate symbols that occur in G and where

there is a positive edge p

→

q if G contains a clause

p(~s) ⇐ ... ∧ q(

t ) ∧ ..., and a negative edge p

−

→

q if

G contains a clause p(~s) ⇐ .. . ∧ ¬q(

t ) ∧ . . . .

To constitute a valid GDL speciﬁcation, a set of

clauses G and its dependency graph Γ must satisfy

the following.

1. There are no cycles involvinga negativeedge in Γ

(this is also known as being stratiﬁed (Apt et al.,

1987; van Gelder, 1989));

2. Each variable in a clause occurs in at least one

positive atom in the body (this is also known as

being allowed (Lloyd and Topor, 1986));

3. If p and q occur in a cycle in Γ and G contains

a clause

p(~s) ⇐ b

(

) ∧ . . . ∧ q(v

,... , v

) ∧ . . . ∧ b

(

)

then for every i ∈ {1, . . . , k},

• v

is variable-free, or

• v

is one of s

,... , s

(:=~s), or

• v

occurs in some

(1 ≤ j ≤ n) such that b

does not occur in a cycle with p in Γ.



Stratiﬁed logic programs are known to admit a

speciﬁc standard model; we refer to (Apt et al., 1987)

for details and just mention the following properties:

1. To obtain the standard model, clauses with vari-

ables are replaced by their (possibly inﬁnitely

many) ground instances.

SPECIFYING MULTIAGENT ENVIRONMENTS IN THE GAME DESCRIPTION LANGUAGE

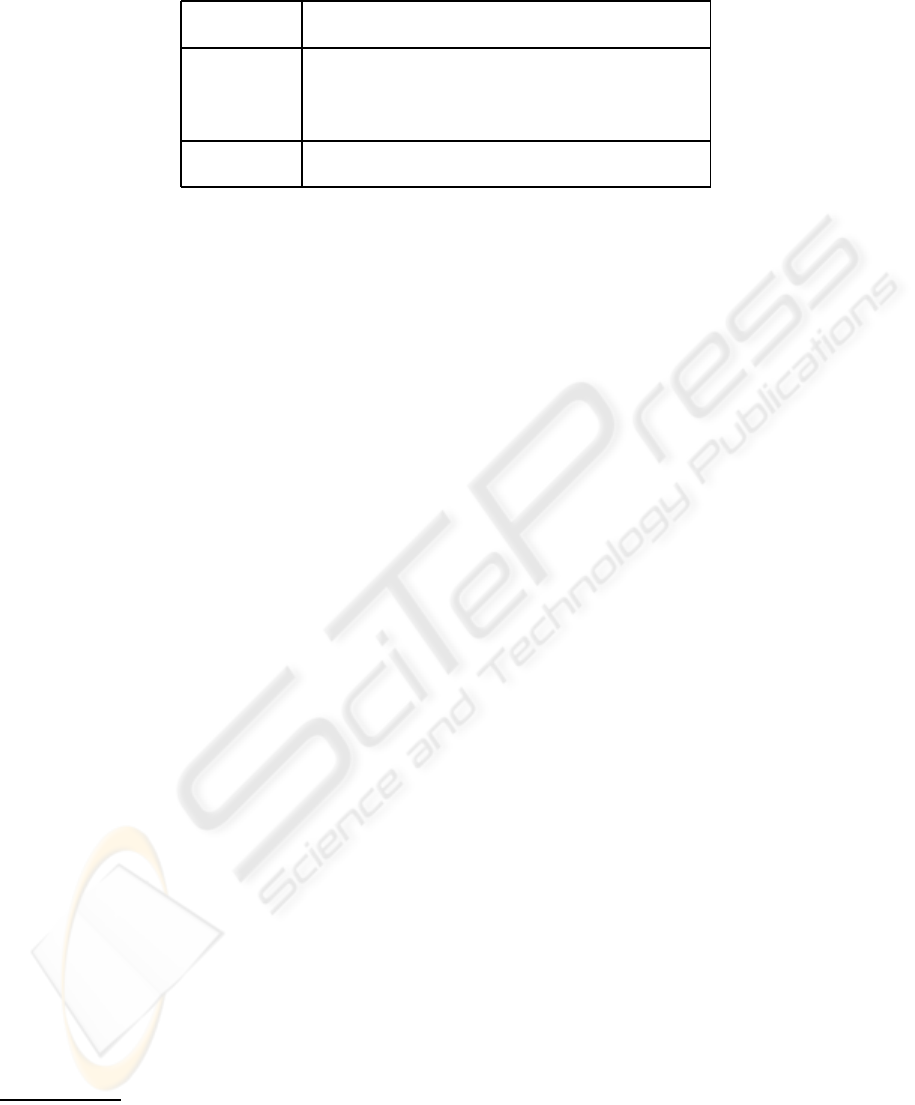
Table 1: GDL keywords.

role(R) R is a player

init(P) P holds in the initial position

true(P) P holds in the current position

legal(R,M) player R has legal move M

does(R, M) player R does move M

next(P) P holds in the next position

terminal the current position is terminal

goal(R, N) player R gets goal value N in the current position

2. Clauses are interpreted as reverse implications.

3. The standard model is minimal while interpret-

ing negation as non-derivability (the “negation-as-

failure” principle (Clark, 1978));

The second and third restriction in Deﬁnition 3 essen-

tially guarantee that a logic program entails a ﬁnite

number of ground atoms via its standard model. This

is necessary to enable agents to make effective use of

a set of game rules.

3.2 GDL Keywords

As a tailor-made speciﬁcation language, GDL uses a

few pre-deﬁned predicate symbols. These are shown

in Table 1 together with their informal meaning. A

further, standard predicate is distinct(X, Y) to ex-

press (syntactic) inequality of two terms.

GDL imposes additional restrictions on the use of

these keywords.

Deﬁnition 4 A valid GDL speciﬁcation is a set of

clauses G that, in addition to the restrictions in Deﬁ-

nition 3, satisﬁes the following conditions.

• role only appears in the head of clauses that

have an empty body;

• init only appears as head of clauses and is not

connected, in the dependency graph for G, to any

of true,legal,does,,,goal;

• true only appears in the body of clauses;

• does only appears in the body of clauses and is

not connected, in the dependency graph for G, to

any of legal,terminal,goal;

• nly appears as head of clauses.



The semantics of this predicate is given by tacitly as-

suming the addition of the clause

distinct(s,t) ⇐

for every pair s,t of syntactically different ground terms.

According to the informal semantics given in (Love

et al., 2006), a GDL speciﬁcation G is to be under-

stood as follows. The derivable instances of role(R)

deﬁne the players. The initial state is composed of

the derivable instances of init(P). In order to deter-

mine the legal moves of a player in any given state,

this state has to be encoded ﬁrst, using the keyword

true. More precisely, let S = {p

,... , p

} be a state

(e.g., the derivable instances of init(P) at the be-

ginning), then G is extended by the clauses

true(p

) ⇐

...

true(p

) ⇐

(1)

Those instances of legal(R, A) which are derivable

from this extended program deﬁne all legal actions A

for player R in state S. In the same way, the clauses

for terminal and goal(R,N) deﬁne termination

and goalhood (of value N for player R) relative to the

encoding of a given state. Determining a state transi-

tion, ﬁnally, requires the encoding of the current state

along with clauses representing a joint move. Specif-

ically, if players r

,... , r

make moves a

,... , a

then

does(r

) ⇐

...

does(r

) ⇐

(2)

must be added to G, and then the derivable instances

of next(P) compose the updated state.

3.3 Multiagent Environments in GDL

GDL provides all necessary features for declarative,

formal descriptions of arbitrary multiagent environ-

ments as deﬁned in Section 2. Of course there are

many possible ways in which any speciﬁc environ-

ment can be axiomatized. We therefore deﬁne two

sets of GDL clauses as logically equivalent if for any

ﬁnite set of ground clauses (1) and (2) added, the two

standard models of the two resulting logic programs

agree on the interpretation of all GDL keywords. Be-

fore we can show how to formalize multiagent en-

vironments in GDL, we need the following syntactic

deﬁnitions.

ICAART 2009 - International Conference on Agents and Artificial Intelligence

For any ﬁnite subset S = {p

,... , p

} ⊆ Σ of a set

of ground terms, the following conjunction axioma-

tizes S as the current state:

true

def

= true(p

) ∧ . . . ∧ true(p

) ∧ ¬p

(3)

Here, p

is an auxiliary predicate, one for every ﬁ-

nite S ⊆ Σ, whose purpose is to ensure that the con-

junction does not hold for states that are strict super-

sets of S:

⇐ true(X)∧

distinct(X, p

) ∧ . . . ∧ distinct(X, p

)

Hence, p

is true for any state in which at least one

state component X is true that differs syntactically

from any of p

,... , p

, that is, the elements of S.

This ensures that the conjunction deﬁned in (3) char-

acterizes state S exactly.

Furthermore, for any function A : {r

,... , r

} 7→

Σ, where r

,... , r

∈ Σ, the following conjunction ax-

iomatizes A as a joint action:

does

def

= does(r

,A(r

)) ∧ . . . ∧ does(r

,A(r

))

We are now ready to show how GDL can be used

to axiomatize multiagent domains.

Deﬁnition 5 Let E = (R,s

,t, l, u, g) be a multi-

agent environment based on ground symbolic expres-

sions Σ, then any valid set of GDL clauses is an ax-

iomatic description of E if it is logically equivalent

to the following.

• role(r) ⇐ for each r ∈ R;

• init(p) ⇐ for each p ∈ s

;

• terminal ⇐ S

true

for each S ∈ t;

• legal(r, a) ⇐ S

true

for each (r, a, S) ∈ l;

• () ⇐ A

does

∧ S

true

for each p ∈ u(A, S) and A :

R 7→ Σ, S ⊆ Σ;

• goal(r,n) ⇐ S

true

for each (r, n, S) ∈ g.



It is important to realize that this direct axiomatiza-

tion, where all relations and functions are encoded

explicitly, is used solely to deﬁne the intended se-

mantics. In practice, of course, a domain can be

described in a much more compact manner, using

variables, logical equivalence, and possibly auxiliary

predicates. As an example, Figure 2 depicts a com-

plete GDL speciﬁcation of the multiagent environ-

ment introduced in Section 2. It is not too difﬁcult

to verify that this is a valid set of clauses according to

Deﬁnition 3 and 4 and that it is indeed a correct ax-

iomatic description of this domain according to Deﬁ-

nition 5.

The speciﬁcation of the Game Description Lan-

guage in (Love et al., 2006) lacks a fully formal deﬁ-

nition of the intended meaning of a speciﬁcation. This

is why there are no formal grounds on which it could

actually be proved that Deﬁnition 5 yields a correct

description of a multiagent environment. In fact, we

can and will use our formal concept of a multiagent

domain to provide just this precise semantics for GDL

in terms of a transition system.

4 A MULTIAGENT SEMANTICS

FOR GDL

In the preceding section, we have shown how GDL

provides a declarative, compact language to formally

describe a large class of multiagent environments in

a machine processable fashion. In this section, we

show how the abstract model of a multiagent environ-

ment can in turn be used to provide a formal semantics

for GDL in terms of a transition system. In this way

we make precise what is only informally described

in (Love et al., 2006).

Any valid game description G in GDL contains

a ﬁnite set of function symbols, including constants,

which implicitly determines a (usually inﬁnite) set of

ground terms. This set constitutes the symbol base Σ

in the transition-based semantics for G. The syntactic

restrictions in GDL ensure ﬁnite derivability, so that

each state, the set of roles, etc. are all ﬁnite subsets

of Σ. The following deﬁnition of the semantics of

a GDL description is straightforwardly obtained by

reversing the mapping from a multiagent environment

into GDL (cf. Deﬁnition 5).

Deﬁnition 6 Let G be a valid GDL speciﬁca-

tion, whose signature determines the set of ground

terms Σ. The semantics of G is the multiagent envi-

ronment (R,s

,t, l, u, g) where

• R = {r ∈ Σ : G |= role(r)};

• s

= {p ∈ Σ : G |= init(p)};

• t = {S ∈ 2

: G∪ S

true

|= terminal};

• l = {(r,a, S) : G∪ S

true

|= legal(r, a, S)}, where

r ∈ R, a ∈ Σ, and S ∈ 2

;

• u(A, S) = {p ∈ Σ : G∪ A

does

∪ S

true

|= ()}, for all

A : (R 7→ Σ) and S ∈ 2

;

• g = {(r, n, S) : G ∪ S

true

|= goal(r, n, S)}, where

r ∈ R, n ∈ N , and S ∈ 2



This deﬁnition provides a formal semantics for GDL

in terms of abstract multiagent environments. Finite

derivability in valid GDL speciﬁcations implies that

Below, entailment (|=) is via the standard model of a

set of clauses.

SPECIFYING MULTIAGENT ENVIRONMENTS IN THE GAME DESCRIPTION LANGUAGE

role(ag

) ⇐

role(ag

) ⇐

role(ag

) ⇐

init(at(ag

,1, 1)) ⇐

init(at(ag

,5, 1)) ⇐

init(at(ag

,1, 5)) ⇐

terminal ⇐ true(at(ag

,X,Y)) ∧ true(at(ag

,X,Y))

terminal ⇐ true(at(ag

,X,Y)) ∧ true(at(ag

,X,Y))

terminal ⇐ ¬remain

remain ⇐ true(at(ag

,X,Y))

legal(R,stay) ⇐ true(at(R,X, Y))

legal(ag

,exit) ⇐ ¬terminal ∧ true(at(ag

,1, 1))

legal(ag

,exit) ⇐ ¬terminal ∧ true(at(ag

,5, 1))

legal(ag

,exit) ⇐ ¬terminal ∧ true(at(ag

,1, 5))

legal(R,move(D)) ⇐ ¬terminal ∧ true(at(R,U, V)) ∧ adjacent(U,V,D, X, Y)

adjacent(X, Y

,north, X, Y

) ⇐ co(X) ∧ succ(Y

)

adjacent(X, Y

,south, X, Y

) ⇐ co(X) ∧ succ(Y

)

adjacent(X

,Y, east,X

,Y) ⇐ co(Y) ∧ succ(X

)

adjacent(X

,Y, west,X

,Y) ⇐ co(Y) ∧ succ(X

)

co(1) ⇐ co(2) ⇐ co(3) ⇐ co(4) ⇐ co(5) ⇐

succ(1,2) ⇐ succ(2,3) ⇐ succ(3,4) ⇐ succ(4,5) ⇐

next(at(R,X, Y)) ⇐ does(R,stay) ∧ true(at(R,X,Y))

next(at(R,X, Y)) ⇐ does(R,move(D)) ∧ true(at(R, U, V)) ∧ adjacent(U,V,D, X, Y) ∧ ¬capture(R)

next(at(ag

,X, Y)) ⇐ true(at(ag

,X, Y)) ∧ capture(ag

)

capture(ag

) ⇐ true(at(ag

,X, Y)) ∧ true(at(R,U, V)) ∧ does(ag

,move(D

))∧

does(R,move(D

)) ∧ adjacent(X,Y,D

,U, V) ∧ adjacent(U,V,D

,X, Y)

goal(R,0) ⇐ role(R) ∧ ¬terminal

goal(R,0) ⇐ role(R) ∧ distinct(R,ag

) ∧ terminal ∧ ¬remain

goal(R,100) ⇐ role(R) ∧ distinct(R,ag

) ∧ terminal ∧ true(at(ag

,X, Y))

goal(ag

,0) ⇐ terminal ∧ true(at(ag

,X, Y))

goal(ag

,100) ⇐ terminal ∧ ¬remain

Figure 2: A complete, formal description of the multiagent environment of Figure 1.

the entailment relation is decidable, which in turn en-

sures that the deﬁnition of the semantics is effective.

In the preceding section we have seen that one

and the same multiagent environmentcan be axiomat-

ically described in many differentways. With the help

of Deﬁnition 6 it is now easy to verify that two logi-

cally equivalent GDL descriptions (as deﬁned in Sec-

tion 3.3) describe exactly the same environment.

Proposition 7 The semantics of two logically equiv-

alent, valid GDL descriptions coincide.

Proof: By deﬁnition, two logically equivalent GDL

descriptions agree on the interpretation of all GDL

keywords for all ﬁnite additions of clauses (1) and (2).

It is easy to see, then, that the various components

of their semantics according to Deﬁnition 6 must be

identical.

Based on this result it is also straightforward to

prove that Deﬁnition 6 indeed provides the comple-

ment to the encoding of a multiagent environment in

GDL.

Proposition 8 Let E be a multiagent environment

and G any axiomatic description thereof, then the se-

mantics of G is E.

Proof: Consider the generic encoding of E given

in Deﬁnition 5. It is easy to verify that the standard

model for this set of clauses, augmented by any ﬁ-

nite set of facts about relations true and does (cf.

clauses (1) and (2), respectively, in Section 3.2), de-

termines a semantics (R, s

,t, l, u, g) via Deﬁnition 6

which equals E . The claim follows from Proposi-

tion 7 and the fact that any GDL encoding for E is

logically equivalent to the generic clauses given in

Deﬁnition 5.

ICAART 2009 - International Conference on Agents and Artificial Intelligence

5 DISCUSSION

We have shown how the Game Description Language,

developed in the context of General Game Playing,

can be readily used as a declarative language to pro-

vide compact and machine processable speciﬁcations

of a large class of multiagent environments. This can

be applied to formalize the rules, for example, of an

e-marketplace, of publicly accessible agent platforms

on the Internet, of problem domains used in agent

competitions, etc. By automatically processing these

speciﬁcations, autonomous agents can fully automat-

ically learn how to participate in a new or modiﬁed

environment without the need to be (re-)programmed.

Moreover, successful off-the-shelf generalgame play-

ing systems can be readily employed as intelligent

agents for these environments.

It is interesting to note that GDL has been orig-

inally developed as problem speciﬁcation language

for a competition (Genesereth et al., 2006), much

like the Planning Domain Description Language

(PDDL) (McDermott, 2000), which today is a quasi

standard for the speciﬁcation of planning domains.

GDL can be viewed as a generalization of PDDL to

domains with multiple agents, because solving a plan-

ning problem can be understood as playing a single-

player game. Indeed, most features of current ver-

sions of PDDL can be expressed in GDL, though

with one notable exception: sensing actions are not

included in the current version of GDL. Although

a GDL speciﬁcation leaves agents with uncertainty

about how the world evolves (an agent can decide on

its own actions but not on those of all other agents),

the language has been written for games without in-

formation asymmetry. An important research issue

for the near future is to extend the Game Description

Language so as to support descriptions of games with

asymmetric information and sensing actions, which

is a typical feature of card games, for instance. This

would then provide a suitable formalization language

for an even larger class of multiagent environments

than considered in this paper.

In the second part of the paper, we have used the

concept of a multiagent environment to provide a for-

mal, transition-based semantics for GDL. With this

we have made precise what is only informally de-

scribed in (Love et al., 2006). Our semantics for GDL

in terms of multiagent environments is related to an

existing formal characterization of GDL by a game

structure (van der Hoek et al., 2007). The main dif-

ference of the latter in comparison to our work are:

• It is restricted to propositional GDL;

• It puts further restrictions on GDL, such as not

allowing predicate init to occur in clause with

non-empty bodies;

• It uses an inductive deﬁnition of the set of all

states in order to obtain only those which are

reachable from the initial state. Since it is pos-

sible to give valid GDL speciﬁcations of games

that do not terminate, this deﬁnition would be un-

decidable in the general setting.

These restrictions have been imposed because the fo-

cus in (van der Hoek et al., 2007) lies on the use of

Temporal Logic for the purpose of verifying proper-

ties of games, such as termination or winnability. In

contrast to this, the semantics given in the present pa-

per covers full GDL.

ACKNOWLEDGEMENTS

We are grateful to the anonymous reviewers of this

paper for helpful suggestions. This research was par-

tially supported by Deutsche Forschungsgemeinschaft

under Contract TH 541/16-1.

REFERENCES

Apt, K., Blair, H. A., and Walker, A. (1987). Towards a

theory of declarative knowledge. In Minker, J., editor,

Foundations of Deductive Databases and Logic Pro-

gramming, chapter 2, pages 89–148. Morgan Kauf-

mann.

Clark, K. (1978). Negation as failure. In Gallaire, H. and

Minker, J., editors, Logic and Data Bases, pages 293–

322. Plenum Press.

Clune, J. (2007). Heuristic evaluation functions for general

game playing. In Proceedings of the AAAI National

Conference on Artiﬁcial Intelligence, pages 1134–

1139, Vancouver. AAAI Press.

Finnsson, H. and Bj¨ornsson, Y. (2008). Simulation-based

approach to general game playing. In Proceedings

of the AAAI National Conference on Artiﬁcial Intel-

ligence, pages 259–264, Chicago. AAAI Press.

It is worth noting that this does not contradict the ﬁnite

derivability property of valid GDL speciﬁcations, which

just implies that all local reasoning problems are decidable.

More speciﬁcally, given a particular state it is decidable

whether an action is possible, and given a joint action it

is also decidable what properties hold in the updated state,

etc. On the other hand, GDL is expressive enough to de-

scribe any Turing machine as a “game” using clauses like

init(head(0)) ⇐

next(head(succ(X))) ⇐ true(head(X)) ∧

does(tm,move forward)

Hence, reachability of states is generally undecidable in

GDL.

SPECIFYING MULTIAGENT ENVIRONMENTS IN THE GAME DESCRIPTION LANGUAGE

Genesereth, M., Love, N., and Pell, B. (2006). General

game playing. AI Magazine, 26(2):73–84.

Kuhlmann, G., Dresner, K., and Stone, P. (2006). Au-

tomatic heuristic construction in a complete general

game player. In Proceedings of the AAAI National

Conference on Artiﬁcial Intelligence, pages 1457–

1462, Boston. AAAI Press.

Lloyd, J. (1987). Foundations of Logic Programming.

Series Symbolic Computation. Springer, second, ex-

tended edition.

Lloyd, J. and Topor, R. (1986). A basis for deductive

database systems II. Journal of Logic Programming,

3(1):55–67.

Love, N., Hinrichs, T., Haley, D., Schkufza, E., and

Genesereth, M. (2006). General Game Playing:

Game Description Language Speciﬁcation. Tech-

nical Report LG–2006–01, Stanford Logic Group,

Computer Science Department, Stanford University,

353 Serra Mall, Stanford, CA 94305. Available at:

games.stanford.edu

McDermott, D. (2000). The 1998 AI planning systems com-

petition. AI Magazine, 21(2):35–55.

Schiffel, S. and Thielscher, M. (2007). Fluxplayer: A suc-

cessful general game player. In Proceedings of the

AAAI National Conference on Artiﬁcial Intelligence,

pages 1191–1196, Vancouver. AAAI Press.

van der Hoek, W., Ruan, J., and Wooldridge, M. (2007).

Strategy logics and the game description language. In

Proceedings of the Workshop on Logic, Rationality

and Interaction, Bejing, China.

van Gelder, A. (1989). The Alternating Fixpoint of Logic

Programs with Negation. In Proceedings of the 8th

Symposium on Principles of Database Systems, pages

1–10. ACM SIGACT-SIGMOD.

ICAART 2009 - International Conference on Agents and Artificial Intelligence