SKY DETECTION IN CSC-SEGMENTED COLOR IMAGES

Frank Schmitt and Lutz Priese

University of Koblenz-Landau

∗

, Koblenz, Germany

Keywords:

Sky detection, CSC.

Abstract:

We present a novel algorithm for detection of sky areas in outdoor color images. In contrast to sky detectors

in literature that detect only blue, cloudless sky we intend to detect all sorts of sky, i.e. blue, clouded and

partially clouded sky. Our approach is based on the analysis of color, position, and shape properties of color

homogeneous spatially connected regions detected by the CSC. An evaluation on a set of images acquired

under different weather conditions proves the quality of the proposed system.

1 INTRODUCTION

For many applications in image processing accurate

and fast detection of the sky is helpful. After the

sky has been detected we can conclude on the content

of the image and extract information about weather

and illumination conditions during image acquisition.

Knowledge about the sky also often helps to constrain

the search domain for later, more complicated image

recognition algorithms.

In images of urban regions the lower border of sky

areas often equals the top border of buildings. Those

borders can give ﬁrst clues for pose estimation, i.e.

the detection of position and orientation of the cam-

era relative to the building. For this task it is important

to ﬁnd the sky reliable under all weather conditions,

i.e., cloudless, partially clouded or overclouded. On

the other hand, it is not important to ﬁnd smaller iso-

lated sky areas below such borders, e.g. under arch-

ways. The sky detection system introduced here is

optimized for such an application scenario.

In the ﬁrst steps of the algorithm, the input im-

age is smoothed and segmented by the CSC, a re-

gion growing segmentation method introduced by

Rehrmann and Priese (Rehrmann and Priese, 1998).

The CSC partitions the image into spatially con-

nected, color homogeneous regions, called segments.

Each segment is analyzed individually regarding its

mean color and a sky probability is attached. In a ﬁ-

∗

This work was supported by the DFG under grant

PR161/12-1 and PA 599/7-1

nal step spatial information typical for urban scenes

is added to the probability map and all segments are

classiﬁed into sky and non-sky.

2 RELATED AND PREVIOUS

WORK

Previous work on sky detection by other groups has

the goal to detect the pure blue sky, thus, the image of

the atmosphere. Clouds are by this deﬁnition explic-

itly not part of the sky and therefore not to be detected.

Luo and Etz (Luo and Etz, 2002) state that the

color of the sky changes gradually from a dark blue

in the zenith to a bright, sometimes almost white, blue

near the horizon. They model the values in three color

channels along straight lines from zenith to horizon

as three one-dimensional functions and analyze these

functions with regard to characteristic properties of

the sky.

Gallagher et. al (Gallagher et al., 2004) ﬁrst gen-

erate an initial sky probability map based on classiﬁ-

cation of color values. In a second stage they model

the spatial variation of pixels initially classiﬁed as

sky. They calculate for each color channel a two-

dimensional polynomial that approximates the values

of pixels with high sky probability. By comparison

between values of pixels in the images and the corre-

sponding values of the polynomial the ﬁnal sky clas-

siﬁcation is generated.

Zafarifar and de With (Zafarifar and de With,

101

Schmitt F. and Priese L. (2009).

SKY DETECTION IN CSC-SEGMENTED COLOR IMAGES.

In Proceedings of the Fourth International Conference on Computer Vision Theory and Applications, pages 101-106

DOI: 10.5220/0001560601010106

 SciTePress

2006) use sky detection in the context of image qual-

ity enhancement in video data. Their system gen-

erates a sky probability map based on texture, color

values, gradients, and vertical position in the image.

They achieve very good results, however, they only

detect blue sky and therefore their system gives low

sky probability in clouds.

However, in many parts of the world clouded sky

is very common. Thus, systems which restrict them-

selves to blue sky detection are restricted in practica-

bility. Our new system detects the total sky under all

weather conditions.

First ideas of the presented approach – not includ-

ing the following major improvements based on the

analysis of segment’s shape and gradients – have been

presented in the German workshop “Farbworkshop

2008” (Schmitt and Priese, 2008).

3 CHARACTERISTICS OF SKY

In systems for the detection of a cloudless sky one

may assume that the sky is free of large gradients but

shows a continuous brightness gradient. As we regard

clouds as part of the sky we can not make such an

assumption. Our sky detector is thus based on differ-

ent assumptions and observations of characteristics of

the sky in color images in urban regions. We assume

that the images to be analyzed have been acquired ho-

rizontally so that the sky is at the top of the image.

Where this assumption does not apply one may em-

ploy algorithms for horizon estimation as introduced

in (Ettinger et al., 2002) or (Feﬁlatyev et al., 2006).

Beside the position in the image, the color is the

second characteristic property of the sky. The color

can range from a pure white over different kinds of

gray inside clouds to shades of blue of different satu-

ration and brightness in cloudless regions. We further

assume, that all segments belonging to the sky have a

vertical connection to the upper border of the image,

either directly or through other segments recognized

as sky.

If one chooses, e.g., split-and-merge (Horowitz

and Pavlidis, 1974) (SaM) as a segmentation tech-

nique and the sky disintegrates into several seg-

ments the borders between those segments show large

straight lines. Those reﬂect the underlying quad-tree

structure of the SaM algorithm. This will not hap-

pen with the CSC segmentation technique. The bor-

ders of two segments of the sky almost always show

an irregular contour without straight lines. However,

the border between sky and buildings is usually build

from straight lines. This leads to further classiﬁcation

criteria.

4 THE ALGORITHM

4.1 Basic Concepts

Our algorithm is directly motivated by the observa-

tions of the previous paragraph.

In a ﬁrst step we smooth the image and segment it

into spatially connected, color homogeneous regions.

In the next step we start at the top border of the image

and search for segments whose mean color is suitable

for sky.

However, an analysis of mean color and position

is insufﬁcient. Such a straight forward method also

classiﬁes white, gray, and blue objects outside the sky

- but immediately below the horizon - as sky. To re-

duce the number of those false-positive classiﬁcations

we have to add another step where the shape of possi-

ble sky segments is analyzed.

4.2 Pre-processing and Segmentation

The input image is ﬁrst smoothed with one iteration of

a 3×3 Kuwahara-ﬁlter(M. Kuwahara, K. Hachimura,

S. Eiho, and M. Kinoshita, 1976). This non-linear

ﬁlter sharpens borders and simultaneously smooths

within homogeneous regions. The ﬁltered image is

segmented into spatially connected, color homoge-

neous regions with the CSC.

The CSC is a region growing segmentation

method steered by a hierarchy of overlapping is-

lands. If two overlapping partial segments are simi-

lar enough they are merged into a new segment. Else

the common sub-region is split between them. As the

decision whether to split or to merge two regions is

not only based on a common border but a common

sub-region, the results are more stable than in con-

ventional region growing methods. The structure of

the island hierarchy makes the CSC inherently paral-

lel. Also, there is no need for spreading seed points

in the image whose position inﬂuences the outcome

of the segmentation in conventional region growing

methods.

It is important to choose the parameters of the

CSC such that an over-segmentation (areas belonging

together are split into several segments) is more likely

than an under-segmentation (areas not belonging to-

gether are merged into one segment) as an additional

classiﬁcation of the found segments has to been done

anyway.

The CSC segmentation can be applied either in

HSV color space based on color similarity tables

(Rehrmann, 1994) or in L*a*b* color space where

similarity between two shades of color is calculated

using the Euclidean distance. For the experiments in

VISAPP 2009 - International Conference on Computer Vision Theory and Applications

102

this paper we have chosen the L*a*b* color space

with a threshold of 12. The result of the CSC is a

label image where the value at every pixel is set to the

label of the segment it belongs to.

4.3 Characteristics of Segments

Let a segment S be represented as a set of spatially

connected pixels. The upper border b

(S) consists of

all coordinates (x, y) such that the pixel at (x, y) is in-

side S and the pixel at (x, i) is outside S for all i ∈ N

with i < y. (As customary in computer vision, we use

positivecoordinates(x, y) where (0, 0) denotes the left

upper corner of the image.)

The color of S is the mean color of all pixels be-

longing to S. As segments are color homogeneous,

the problem that averaging may create false colors

does not occur.

The mean vertical gradient of S is a measure de-

scribing the brightness gradient at the common border

between S and its upper neighbor segments. It is cal-

culated as the average brightness difference between

pixels at b

(S) and their direct upper neighbor pixels.

If no upper neighbors exist the mean vertical gradient

is set to 0. A low mean vertical gradient is a strong

clue for a segment border generated during splitting

of a color gradient into several segments. Such bor-

ders are normally more or less arbitrary and typical

for a segmentation within the sky.

The mean bounded second derivative of b

(S) is a

measure which describes whether the top border of S

is build of straight lines or rather formed irregularly.

It is calculated as follows:

Let x

min

be the x-coordinate of the leftmost and

max

of the rightmost pixel in S. For each i ∈ N

in [x

min

, x

max

] exists exactly one coordinate with x-

component i in b

(S). We can therefore regard b

(S)

as a function of x where b

(S, x) := y if (x, y) ∈ b

(S)

and undeﬁned else. The function

(S, x) := b

(S, x − 1) − 2· b

(S, x) + b

(S, x + 1)

is the discrete second derivative of b

for segment S

at position x.

|δ

(S, x)| is low at straight border segments and

high at irregularly formed areas. Thus, an obvious ap-

proach would be to average |δ

(S, x)| over the width

of S in order to get a measure for the straightness

of S. However, this approach leads to the prob-

lem that within a polygon, that consists of few con-

nected straight lines, the corner points may contribute

too high values. We therefore use bounded values

as follows: Let m(S, x) := 1 for |δ

(S, x)| ≥ 1 and

m(S, x) := 0 elsewhere. The mean bounded second

derivative of the top border of S is calculated as

∑

(x,y)∈b

(S)

m(S, x)

∑

(x,y)∈b

(S)

4.4 Color Analysis

A classiﬁcation of segments as sky solely by their

color is obviously impossible. There are usually sev-

eral objects (or reﬂections) in an image that do not

belong to the sky but have a color which could also

occur in the sky. Thus, in this phase we only deter-

mine whether the mean color of a segment may occur

also in the sky. For such a task it will not help to

train a classiﬁer with many examples of sky and non-

sky segments. The result will not be disjunctive as all

colors which can occur in the sky can occur in other

image regions as well. Instead, we were able to deter-

mine by manual analysis of sample images a simple

and rather compact subspace of the HSV color space

which includes all colors occurring in sky.

Our experiments have shown that it sufﬁces to call

a HSV value hsv sky colored if it meets at least one of

the following conditions:

• hsv.saturation < 13 and hsv.value > 216

• hsv.saturation < 25 and hsv.value > 204 and

hsv.hue > 190 and hsv.hue < 250

• hsv.saturation < 128 and hsv.value > 153 and

hsv.hue > 200 and hsv.hue < 230

• hsv.value > 88 and hsv.hue > 210 and hsv.hue <

220

The listed hue values are to some degree dependent

on the cameras used.

4.5 Analysis of Position and Shape

Let L

and L

be two (initially empty) lists of seg-

ments already classiﬁed as sky (L

) or as candidates

) for sky. Segments whose mean color is sky col-

ored and for which the condition holds that at least

half of their top border touches the top border of the

image are added to L

. All segments touching the

lower border of at least one of the segments in L

are

added to a L

. For each segment S in L

we check

three criteria:

1. the color of S is sky colored,

2. at least two thirds of the top border of S touches

either the top border of the image or segments in

3. at least one of the following conditions is satisﬁed:

(a) the area of S contains less than 500 pixel (we

skip shape analysis for such small segments)

SKY DETECTION IN CSC-SEGMENTED COLOR IMAGES

103

(b) the mean vertical gradient of S is below 25

(S) is

bigger than 0.3.

If all three conditions are satisﬁed S is classiﬁed

as sky and the lists L

, L

are updated. Otherwise, S is

removed from L

. The algorithm terminates when the

candidate list is empty.

At this stage, all segments which belong to sky

and have a connection to the top border of the image

(either a direct connection or through other sky seg-

ments) should have been classiﬁed as sky. However,

in rare cases it may occur that, e.g., a cloud matches

conditions 1 and 2 but not condition 3 and, thus, has

been falsely classiﬁed as non-sky. Such cases are de-

tected and ﬁxed in a post-processing step where all

non-sky segments which satisfy conditions 1 and 2

and which are completely surrounded by sky are clas-

siﬁed as sky as well.

5 EVALUATION

For an evaluation 179 images of the campus of our

university have been acquired under different weather

conditions. Some examples are shown in appendix A.

To get a ground truth (GT) we have manually anno-

tated the sky to copies of those images. Our evalua-

tion compares the detected sky with this ground truth

sky with two measures: The coverability rate (CR)

measures how much of the true sky is detected by the

algorithm. The error rate (ER) measures how much

of the area detected as sky is not part of the true sky.

Let S denote the detected sky and GT the ground truth

sky. Then both measures are deﬁned as

CR(S, GT) :=

|S∩ GT|

|GT|

, ER(S, GT) :=

|S− GT|

|S|

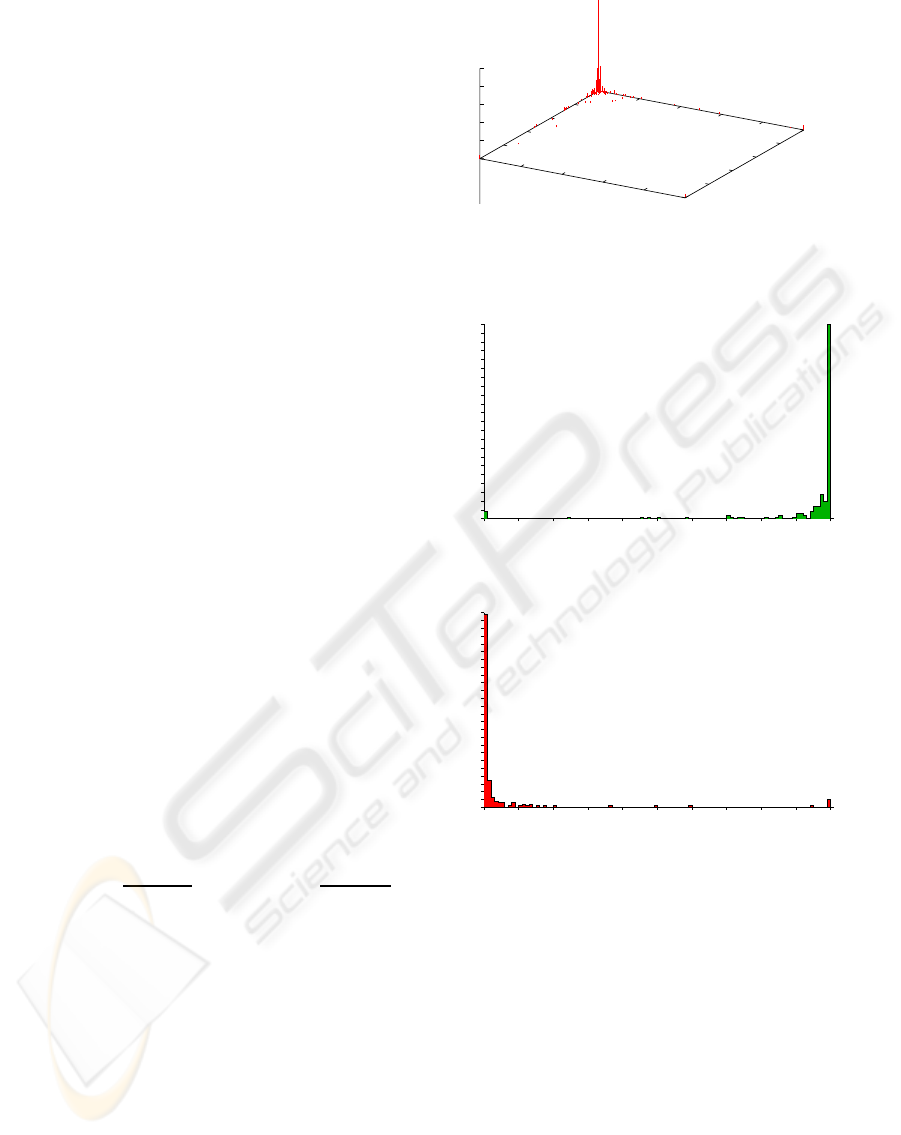
Graphic 1 visualizes our evaluation results. On

the x-axis the error rates are shown, on the y-axis the

coverability rates. The length of a line in z-direction

at position (x,y) tells in how many cases error rate x

and coverabiliy rate y was achieved. Graphics 2 and 3

show the distributions of CR and ER alone.

In 80% of all images, CR is above 0.9 and ER is

below 0.1. In 75% of all images, CR is above 0.95

and ER is below 0.05. Those results clearly show the

quality of the proposed algorithm. The cases where

the error rate is very high correspond in the majority

of cases to images that do not contain any sky at all.

As soon as our algorithm classiﬁes at least one pixel

as sky in those images the error rate becomes 1.0.

0.2

0.4

0.6

0.8

0.2

0.4

0.6

0.8

Quantity

Figure 1: Distribution of CR and ER.

0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1

100

105

110

Figure 2: Distribution of CR.

0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1

100

105

110

115

120

125

Figure 3: Distribution of ER.

6 SUMMARY AND OUTLOOK

We have presented a fast and robust system for

detection of sky in camera images. In contrast to

known systems, our algorithm is able to not only

detect blue but also clouded sky. The presented

algorithm is fast and an quantitative evaluation on a

set of 179 images shows its robustness.

We intend to further improve our sky detector and

will try to automatically detect and split segments

which include both sky and non-sky, see Figure 7 as

an example. Also the detection of images in urban

scenes without any sky at all could be improved.

VISAPP 2009 - International Conference on Computer Vision Theory and Applications

104

REFERENCES

Ettinger, S. M., Nechyba, M. C., Ifju, P. G., and Waszak,

M. (2002). Towards ﬂight autonomy: Vision-based

horizon detection for micro air vehicles. In Florida

Conference on Recent Advances in Robotics 2002.

Feﬁlatyev, S., Smarodzinava, V., Hall, L. O., and Gold-

gof, D. B. (2006). Horizon detection using machine

learning techniques. In ICMLA ’06: Proceedings of

the 5th International Conference on Machine Learn-

ing and Applications, pages 17–21, Washington, DC,

USA. IEEE Computer Society.

Gallagher, A. C., Luo, J., and Hao, W. (2004). Improved

blue sky detection using polynomial model ﬁt. In Im-

age Processing, 2004. ICIP ’04. 2004 International

Conference on, volume 4, pages 2367–2370.

Horowitz, S. and Pavlidis, T. (1974). Picture segmentation

by a directed split-and-merge procedure. In Proceed-

ings of the Second International Joint Conference on

Pattern Recognition, pages 424–433.

Luo, J. and Etz, S. P. (2002). A physical model-based ap-

proach to detecting sky in photographicimages. IEEE

Transactions on Image Processing, 11(3):201–212.

M. Kuwahara, K. Hachimura, S. Eiho, and M. Kinoshita

(1976). Processing of ri-angiocardiographic images.

In Preston, K. and Onoe, M., editors, Digital Process-

ing of Biomedical Images, pages 187–202.

Rehrmann, V. (1994). Stabile, echtzeitf¨ahige Farbbil-

dauswertung. PhD thesis, Universit¨at Koblenz-

Landau, F¨olbach Verlag, Koblenz.

Rehrmann, V. and Priese, L. (1998). Fast and robust seg-

mentation of natural color scenes. In Chin, R. T.

and Pong, T.-C., editors, 3rd Asian Conference on

Computer Vision (ACCV’98), number 1351 in LNCS,

pages 598–606. Springer Verlag.

Schmitt, F. and Priese, L. (2008). Himmelsdetektion in

CSC-segmentierten Farbbildern. In Farbworkshop

2008, Aachen.

Zafarifar, B. and de With, P. H. N. (2006). Blue sky

detection for picture quality enhancement. In Ad-

vanced Concepts for Intelligent Vision Systems, vol-

ume 4179/2006 of Lecture Notes in Computer Sci-

ence, pages 522–532. Springer Berlin / Heidelberg.

APPENDIX

Sample Images

In the following images 4 to 6 the input image of our

algorithm is shown on the left and the result of classi-

ﬁcation on the right. White represents segments clas-

siﬁed as sky, gray represents segments which are sky

colored but not classiﬁed as sky, black represents seg-

ments which are not sky colored.

The following picture 7 shows an example where

the algorithm fails to correctly identify the sky. The

segment encircled in red was falsely classiﬁed as sky

as even in the CSC-segmentation phase the white

front was melted into a larger sky segment.

SKY DETECTION IN CSC-SEGMENTED COLOR IMAGES

105

Figure 4: Photo taken at sunshine with fair-weather cloud.

Figure 5: Photo taken in rainy weather.

Figure 6: Sky colored segments in a building front which aren’t classiﬁed as sky due to shape analysis.

Figure 7: Erroneous CSC segmentation: A white building front merges into one segment with the heavily clouded sky.

VISAPP 2009 - International Conference on Computer Vision Theory and Applications

106