VIEW-INDEPENDENT VIDEO SYNCHRONIZATION FROM
TEMPORAL SELF-SIMILARITIES
Emilie Dexter, Patrick P´erez, Ivan Laptev and Imran N. Junejo
IRISA/INRIA - Rennes Bretagne Atlantique, Campus Universitaire de Beaulieu, 35042 Rennes Cedex, France
Keywords:
Video synchronization, Temporal alignment, Self-similarities.
Abstract:
This paper deals with the temporal synchronization of videos representing the same dynamic event from dif-
ferent viewpoints. We propose a novel approach to automatically synchronize such videos based on temporal
self-similarities of sequences. We explore video descriptors which capture the structure of video similarity
over time and remain stable under viewpoint changes. We achieve temporal synchronization of videos by
aligning such descriptors by Dynamic Time Warping. Our approach is simple and does not require point cor-
respondences between views while being able to handle strong view changes. The method is validated on two
public datasets with controlled view settings as well as on other videos with challenging motions and large
view variations.
1 INTRODUCTION
The number and the variety of video recording de-
vices has exploded in recent years from professional
cameras towards digital cameras and mobile phones.
As one consequence of this development, the simul-
taneous footage of the same dynamic scenes becomes
increasingly common for example for sport events
and public performances. The recorded videos of
the same event often differ in viewpoints and camera
motion, hence, providing information that can be ex-
ploited, e.g., for novel view synthesis and reconstruc-
tion of dynamic scenes or for search in video archives.
Synchronization of such videos is the first challenging
and important step to enable such applications.
In the past, video synchronization was mostly ad-
dressed under assumptions of stationary cameras and
linear time transformations. Some works explore es-
timations of spatial and temporal transformations be-
tween two videos (Stein, 1999; Caspi and Irani, 2002;
Ukrainitz and Irani, 2006) while others focus only on
temporal alignment (Rao et al., 2003; Carceroni et al.,
2004; Wolf and Zomet, 2006; Ushizaki et al., 2006).
In the literature, the majority of approaches ex-
ploit spatial correspondences between views either
to estimate the fundamental matrix (Caspi and Irani,
2002) or to use rank constraints on observation matri-
ces as in (Wolf and Zomet, 2006). In contrast, other
methods try to extract temporal features without cor-
respondences as in (Ushizaki et al., 2006) where au-
thors investigate an image-based temporal feature of
image sequence for synchronization. The time-shift is
estimated by evaluating the correlation between tem-
poral features.
Finally, a few papers deal with synchronization of
moving cameras and to the best of our knowledge,
none of these addresses automatic synchronization.
For example in (Tuytelaars and Van Gool, 2004), au-
thors choose manually the 5 independently moving
points because these points have to be tracked suc-
cessfully along all the sequences.
In this work, we address automatic synchroniza-
tion of videos of the same dynamic event without cor-
respondences between views or assumptions on the
time-warping function. We explore a novel temporal
descriptor of videos, fairly stable under view changes
based on temporal self-similarities. Synchronization
is achieved by aligning descriptors by dynamic pro-
gramming.
1.1 Related Work
Our work is most closely related to the methods of
(Cutler and Davis, 2000; Benabdelkader et al., 2004;
Shechtman and Irani, 2007). The notion of self-
similarity is exploited by (Shechtman and Irani, 2007)
to match images and videos or to detect actions in
383
Dexter E., Pérez P., Laptev I. and N. Junejo I. (2009).
VIEW-INDEPENDENT VIDEO SYNCHRONIZATION FROM TEMPORAL SELF-SIMILARITIES.
In Proceedings of the Fourth International Conference on Computer Vision Theory and Applications, pages 383-391
DOI: 10.5220/0001561003830391
Copyright
c
 SciTePress

videos. They compute a local patch descriptor for ev-
ery pixel by correlating the patch centered at a pixel
with its neighborhood. Matching a template image or
an action to another is achieved by finding a similar
set of descriptors.
The notion of temporal self-similarity we explore
in this paper is more related to the works of (Cutler
and Davis, 2000; Benabdelkader et al., 2004). The
authors construct a similarity matrix where each entry
is the absolute correlation score between silhouettes
of moving objects for all pairs of frames. This matrix
is used respectively for periodic motion detection and
gait recognition.
Our method is also related to the approach of (Rao
et al., 2003) by the use of dynamic programming.
In their work, the authors evaluate temporal align-
ment by including Dynamic Time Warping (DTW)
and rank constraints on observation matrices which
allows the use of non-linear time warping functions
between time axes of videos. In contrast to this work
we do not rely on spatial correspondences between
image sequences which are hard to obtain in practice.
1.2 Our Approach
In this paper, we propose a novel approach to auto-
matically synchronize videos of the same dynamic
event recorded from substantially different, static
viewpoints. In contrast to the majority of existing
methods, we do not impose restrictive assumptions as
sufficient background information, point correspon-
dences between views or linear modeling of the tem-
poral misalignment.
We explore self-similarity matrices (SSM) as a
temporal descriptor of video sequences as recently
proposed for action recognition in (Junejo et al.,
2008). Although SSMs are not strictly view-invariant,
they are fairly stable under view changes as illustrated
in Fig. 1(b,d) where SSMs computed for different
views of a golf swing action have a striking similar-
ity despite the difference in the projections depicted
in Fig. 1(a,c). The intuition behind this claim is the
following. If configurations of a dynamic event are
similar at moments t
1
and t
2
, the value of SSM(t
1
, t
2
)
will be low for any view of that event. On the con-
trary, if configurations are different at t
1
and t
2
the
value of SSM(t
1
, t
2
) is likely to be large for most of
the views. Fig. 1 illustrates this idea. Corresponding
SSMs are computed using distances of points on the
hand trajectory illustrated in Fig. 1(a,c). We can ob-
serve that close trajectory points A, B remain close in
both views while the distant trajectory points A and C
have large distances in both projections.
As a result, the same dynamic event produces sim-
A
B
C
time
time
(a) (b)
B
A
C
time
time
(c) (d)
Figure 1: (a) and (c) demonstrate a golf swing action
seen from two different views, and (b) and (d) represent
their computed self-similarity matrices (SSMs) based on 2D
point trajectories. Even though the two views are different,
the structures of the patterns of computed SSMs are similar.
ilar self-similarity matrices where time axes can be
matched by estimating a time-warping transforma-
tion. Furthermore, we suggest aligning sequence de-
scriptors by DTW in order to obtain exhaustive time
correspondences between videos.
The remainder of this paper is organized as fol-
lows: Section 2 introduces self-similarity descriptors
of videos. Section 3 describes descriptor alignment
based on dynamic programming. In Section 4 we
demonstrate results of video synchronization for two
public datasets as well as for our own challenging
videos.
2 VIDEO DESCRIPTORS
In this section, we introduce the temporal description
of videos. First, we describe the computation and the
properties of self-similarity matrices. Then a local de-
scriptor for SSM is proposed for synchronization.
2.1 Self-similarity Matrices
Our main hypothesis is that similarities and dissim-
ilarities are preserved under view changes. As a re-
sult, the same dynamic event recorded from different
views should produce similar structures or patterns
of self-similarity, enabling subsequent video synchro-
nization.
VISAPP 2009 - International Conference on Computer Vision Theory and Applications
384

For a sequence of images I = {I
1
, I
2
, . . . I
T
}, ly-
ing in discrete (x, y, t)-space, the SSM is the square
symmetric distance matrix D (I ) lying in R
T× T
de-
fined as an exhaustive table of distances between im-
age features taken by pair from the set I :
D (I ) = [d
ij
] =




0 d
12
. . . d
1T
d
21
0 . . . d
2T
.
.
.
.
.
.
.
.
.
d
T1
d
T2
. . . 0




(1)
where d
ij
represents a distance between some features
extracted from frames I
i
and I
j
respectively. The di-
agonal corresponds to comparing an image to itself,
hence, is always zero.
The structure or the patterns of the matrix D (I ) is
determined by features and distance measure used to
compute its entries. Different features produce matri-
ces with different characteristics.
In this work, we use the Euclidean distance to
compute the entries d
ij
of the matrix for features ex-
tracted from image sequence. This form of D (I )
is known as the Euclidean Distance Matrix (EDM)
(Lele, 1993). We have considered two different types
of features to compute D (I ): point trajectories and
image-based features.
2.1.1 Trajectory-based Self-similarities
We first consider trajectory-based similarities where
we track points of the moving object. Entries d
ij
are expressed as the Euclidean distance between the
positions of the tracked points for a pair of frames.
The similarity measure between points tracked in the
frames I
i
and I
j
can be computed as:
d
ij
=
∑
k
kx
k
i
− x
k
j
k
2
(2)
where k indicates the point being tracked, and i and j
indicate the frame numbers in the sequence I . These
point trajectory features are used in our experiments
on the motion capture (MoCAP) dataset presented in
Section 4.1 where the tracked points correspond to
joints on the human body. We denote this computed
matrix by SSM-pos.
2.1.2 Image-based Self-similarities
In addition to the trajectory-based self-similarities,
we also propose to use image-based features. In this
regard, we use optical flow vectors or Histogram of
Oriented Gradients (HoG) features (Dalal and Triggs,
2005) to estimate D (I ).
In our experiments, the optical flow is calculated
using the method proposed by Lucas and Kanade (Lu-
cas and Kanade, 1981) either on bounding box cen-
tered around the the foreground object for the public
image sequence dataset or on the entire image for re-
alistic videos. The global optical flow vector is ob-
tained by concatenating flows in both directions.
In contrast to optical flow vectors which express
motions, HoG features, originally used to perform hu-
man detection, characterize the local shape by captur-
ing edge and gradient structures. Our implementation
uses 4 bin histograms for each 5 x 7 blocks defined
on a bounding box around a foreground object for the
public image sequence dataset or on the entire image
in each frame of realistic videos.
For both features, d
ij
is the Euclidean distance be-
tween two vectors corresponding to the frames I
i
and
I
j
. The SSMs computed by HoG features and optical
flow vectors are respectively denoted SSM-hog and
SSM-of.
2.2 Descriptor
As mentioned above, SSM is symmetric positive
semidefinite matrix with zero-value diagonal and has
view-stable structure. For video synchronization, we
need to capture this structure and consequently con-
struct appropriate descriptors.
We opt for a local representation to describe the
self-similarity matrices after observing their proper-
ties. Indeed, global structures of SSM can be influ-
enced by changes in temporal offsets and time warp-
ing. Furthermore the uncertainty of values increases
with the distance from the diagonal due to the increas-
ing difficulty of measuring self-similarity over long
time intervals.
i
T
1
time
time
h
i
h
i,1
h
i,m
Figure 2: Local descriptors of an SSM are centered at ev-
ery diagonal point i = 1...T and rely on a log-polar block
structure. Histograms of gradient directions are computed
separately for each block and concatenated into descriptor
vector h
i
.
As shown in Fig. 2, we compute at each diagonal
point a descriptor based on a log-polar block struc-
ture. We construct a 8-bin histogram of gradient di-
rections for each of 11 blocks and concatenate the
normalized histograms into a descriptor vector h
i
cor-
responding to the frame number i. Finally the video
sequence is represented by the sequence of such de-
scriptors H = (h
1
, ..., h
T
) computed for all diagonal
VIEW-INDEPENDENT VIDEO SYNCHRONIZATION FROM TEMPORAL SELF-SIMILARITIES
385

elements of the SSM.
3 DESCRIPTOR ALIGNMENT
We aim to align the temporal descriptors extracted
from the self-similarity matrices by a classical DTW
algorithm. Such an approach, which was introduced
for warping two temporal signals in particular for
speech recognition (Rabiner et al., 1978), is well-
adapted to our problem of descriptor alignment.
Given two image sequences I
1
and I
2
of the same
dynamic event seen from different view-points, we
compute SSMs and the corresponding global descrip-
tors, H
1
and H
2
. We denote h
1
i
the local descriptor of
I
1
for the frame i. I
1
and I
2
have respectively N and
M frames.
The DTW algorithm aims to estimate the warping
function w between time axes of the two videos. The
warping between frames i and j of both sequences is
expressed as j = w(i).
Given a dissimilarity measure S, where a smaller
value of S(h
1
i
, h
2
j
) indicates greater similarity between
h
1
i
and h
2
j
, we define the cost matrix C as
C = [c
ij
] =

S(h
1
i
, h
2
j
)

. (3)
Each entry of this matrix measures the cost of
alignment between frames i and j of both sequence
descriptors. The best temporal alignment is the set
of pairs {(i, j)} which contributes to the global min-
imum similarity measure. As a consequence, the op-
timal warping w must minimize the accumulated cost
C
T
:
C
T
= min
w
N
∑
i=1
S(h
1
i
, h
2
w(i)
) (4)
To solve (4) using dynamic programming, we
must construct the accumulated cost matrix C
A
from
the cost matrix C . Considering three possible moves
(horizontal, vertical and diagonal) in C for the warp-
ing, we can recursively compute, for each pair of
frames (i, j), C
A
(h
1
i
, h
2
j
) by
C
A
(h
1
i
, h
2
j
) = c
ij
+ min[C
A
(h
1
i−1
, h
2
j
),
C
A
(h
1
i−1
, h
2
j− 1
), C
A
(h
1
i
, h
2
j− 1
)] (5)
Vertical and horizontal moves correspond to associat-
ing one frame in a sequence to two consecutiveframes
in the other sequence whereas diagonal one amounts
to associating two pairs of consecutive images.
The final solution C
T
of (4) is by definition C
T
=
C
A
(h
1
N
, h
2
M
). The warping function, w, is obtained by
tracing back from the pair of frames (N, M) the opti-
mal path in the accumulated cost matrixC
A
. Finally, if
the pair of frames (i, j) belongs to the path, it means
that the i
th
frame of the first sequence I
1
temporally
corresponds to the j
th
frame of the second sequence
I
2
.
As mentioned above, DTW algorithm requires a
distance measure S(·, ·) to evaluate the alignment cost.
We try different distances, including the one proposed
by (Cha and Srihari, 2002) for histograms. However
cost matrices are extremely similar for our descrip-
tors. So, we choose the Euclidean distance to measure
the similarity between descriptors H
1
and H
2
.
4 SYNCHRONIZATION RESULTS
In this section, we present various results on video
synchronization. The first experiments in Section 4.1
and in Section 4.2 aim to validate the method in con-
trolled multi-view settings using: (i) motion capture
(MoCAP) datasets, and (ii) a public image sequence
dataset (Weinland et al., 2007). We finally demon-
strate synchronization results on realistic videos in
Section 4.3.
(a)
(b) (c)
Figure 3: (a) A person figure animated from the CMU mo-
tion capture dataset and two virtual cameras used to simu-
late projections in our experiments. (b) SSM corresponding
to cam1. (c) SSM corresponding to cam2.
4.1 Synchronization on CMU MoCAP
Dataset
We have used 3D MoCAP data from the CMU dataset
(mocap.cs.cmu.edu) to simulate multiple and con-
trolled view settings of the same dynamic action.
Trajectories of 13 points on the human body were
projected to two cameras with pre-defined orienta-
tions with respect to the human body as illustrated in
Fig. 3(a). We need to remove the effect of translation
VISAPP 2009 - International Conference on Computer Vision Theory and Applications
386

(a) (b) (c) (d)
(e) (f) (g) (h)
Figure 4: Synchronization of SSMs for simulated time-shift. (a-d) Synchronization for sequences with overlapping time inter-
vals. (a) Truncated SSM for cam1. (b) Truncated SSM for cam2. (c) Cost matrix representation with the time transformation
estimation (red curve). (d) The time transformation estimation recovers the ground truth transformation (blue curve). (e-h)
Synchronization for sequences with the time interval of one sequence which is contained in the time interval of the second. (e)
Original SSM for cam1. (f) Truncated SSM for cam2. (g) Cost matrix representation with the time transformation estimation
(red curve). (h) The time transformation estimation recovers the ground truth transformation (blue curve).
and scale such that the points are zero-centered.The
points are normalized by x
i
=
x
′
i
kx
′
i
k
, where x
′
i
corre-
sponds to the joints being tracked in frame i and x
i
corresponds to their normalized coordinates. An ex-
ample of the computed SSMs for these two projec-
tions are proposed in Fig. 3(b,c).
For this dataset, trajectory-based SSMs can be
computed and synchronized in presence of simulated
temporal misalignment. We choose to apply the sim-
plest time transformation: the time-shift. We simply
truncate SSMs in order to simulate time-shift. Two
cases are possible: time intervals of both sequences
overlap or the time interval of one sequence is con-
tained in the time interval of the second. In the first
case, one SSM is truncated at the beginning and the
second at the end. In the second case, only one SSM
is truncated at the beginning and the end.
Fig. 4 illustrates synchronization of both of these
cases for the SSMs shown in Fig. 3. We temporally
align descriptors of truncated SSMs by estimating the
optimal path in the cost matrix with the Dynamic
Time Warping algorithm. The optimal path or esti-
mated time transformation, represented by red curves,
recoversalmost perfectly the ground truth transforma-
tion for both proposed examples corresponding to the
truncated SSMs in the Fig. 4(d,h). These experiments
with controlled view settings validate our framework
of video synchronization when time-warping function
is a simple time-shift.
4.2 Synchronization on IXMAS Dataset
Experiments were also conducted using realimage se-
quences from the public IXMAS dataset (Weinland
et al., 2007). This dataset has 5 synchronized views
of 10 different actors performing 11 classes of actions
three times. Positions and orientations are freely cho-
sen by actors. An illustration of this dataset is de-
picted in Fig. 5.
camera 1
camera 2
camera 3
camera 4
camera 5
“check watch” action
camera 1
camera 2
camera 3
camera 4
camera 5
“punch” action
Figure 5: Example frames for two action classes and five
views of the IXMAS dataset.
For this dataset, we compute image-based features
on bounding boxes around the actors. The boxes are
extracted from silhouettes available for each frame of
VIEW-INDEPENDENT VIDEO SYNCHRONIZATION FROM TEMPORAL SELF-SIMILARITIES
387

(a) (b) (c)
Figure 6: Synchronization of nonlinearly time warped sequences. (a) Sequences with very different view conditions are
represented by key-frames. (b) Cost matrix for computed descriptors with the time transformation estimation (red curve).(c)
Synchronization result where the time transformation estimation recovers almost completely the ground truth transformation
(blue curve).
this dataset. Then, we enlarge and resize bounding
boxes in order to avoid border effect in the optical
flow computation and to ensure the same size of fea-
tures along the sequence. We resize the height to a
value equal to 150 pixels and the width is set to the
largest value for the considered sequence. For HoG
features, we use 4 bin histograms for each 5 x 7 block
defined on the bounding box.
As mentioned above, sequences of this dataset are
synchronized. As a consequence, we must simulate
temporal misalignment. Furthermore, sequences of
this dataset, originally used to perform action recog-
nition, can be considered either action-by-action or
as long sequences composed of several successive ac-
tions. In this paper, we propose only experimental re-
sults for an example of long sequence. However, for
action-by-action sequences, we can apply the same
misalignment method as for the MoCAP dataset.
For long image sequences, we can further chal-
lenge the synchronization by applying a nonlinear
time transformation to one of the sequences in addi-
tion to the time-shift. The time of one sequence is
warped by t
′
= acos(bt). An example of synchroniza-
tion for this warping form is depicted in the Fig. 6(c)
where the estimated time transformation is illustrated
by the red curve and does almost perfectly recover the
ground truth transformation (blue curve) despite the
drastic view variation between image sequences seen
in Fig. 6(a).
We notice that the beginning and the end of the
estimated time transformation do not correspond ex-
actly with the ground truth. This is due to the fact
that DTW estimation assumes, wrongly, that the ad-
missible paths end at (N, M). Despite the false corre-
spondences that this constraint causes, the algorithm
is able to recover a large part of the ground truth.
However, these results demonstrate that our approach
supports linear and nonlinear time transformations
even under drastic view variations between image se-
quences.
4.3 Synchronization on Natural Videos
We have tested the proposed framework to synchro-
nize realistic videos with moving objects or human
activities. For these image sequences, we compute
optical flow between consecutive frames and estimate
corresponding self-similarity matrices and descrip-
tors.
4.3.1 Sequence with Moving Objects
In the first experiment we have used videos of mov-
ing objects as illustrated in Fig. 8(a). The sequences
represent two balls bouncing on a table from two dif-
ferent viewpoints: a top view and a side view. An
illustration of the scene configuration is proposed in
Fig. 7 where green and purple curves represent ball
trajectories. Synchronization results for this pair of
sequences are presented in Fig. 8(c). The original
transformation between the two videos, which is a
time-shift, is partially recovered. In fact, at the be-
ginning and at the end of both sequences, there is no
motion which leads to misalignment due to the lack
of temporal information.
Figure 7: Scene configuration of the videos with two balls
bouncing on a table.
However, our approach has difficulties for peri-
odic motion such as walking or running. Indeed,
VISAPP 2009 - International Conference on Computer Vision Theory and Applications
388

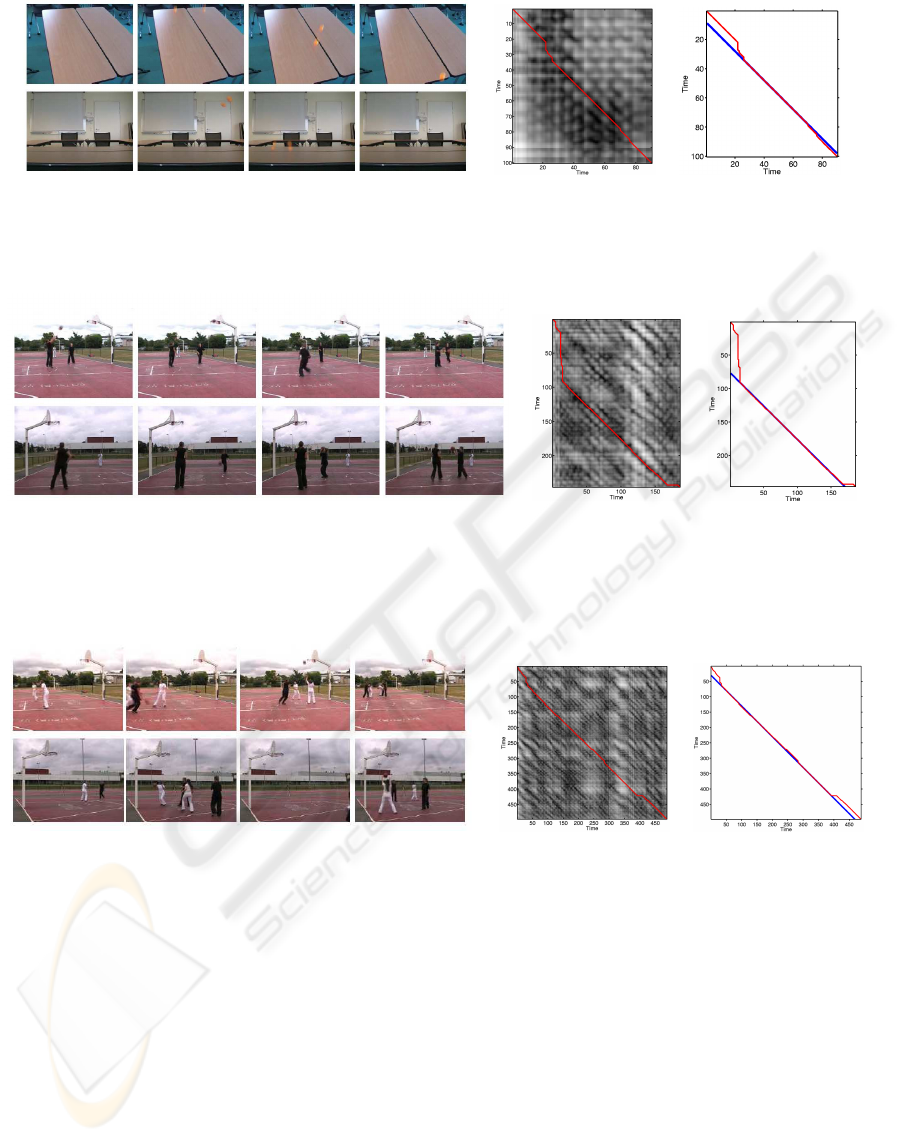
(a) (b) (c)
Figure 8: Synchronization of videos with moving objects. (a) Two balls bounce on a table seen from the top (upper row) and
from the side (lower row). (b) Cost matrix with the time transformation estimation (red curve). (c) Synchronization result
with the time transformation estimation and the ground truth in blue.
(a) (b) (c)
Figure 9: Synchronization of videos of basketball with two players. (a) The upper row represents the first side view whereas
the lower row represents the opposite view. The players always appear in the field of view of cameras. (b) Cost matrix with
the time transformation estimation (red curve). (c) DTW estimation recovers the original transformation (blue curve).
(a) (b) (c)
Figure 10: Synchronization of videos of basketball with four players.(a) The upper row represents the first side view whereas
the lower row represents the opposite view. The players can appear and disappear along the sequences. (b) Cost matrix with
the time transformation estimation red curve). (c) DTW estimation recovers the original transformation (blue curve).
periodic motions induce periodic structures in corre-
sponding self-similarity matrices and cause ambigui-
ties for the DTW algorithm. When motion is almost
periodic as in Fig. 8(a), the performance of our ap-
proach depends on the length of the time-shift. As
in our example the time-shift is short, ambiguities are
limited.
4.3.2 Sequences with Human Activities
In the second experiment we consider outdoor basket-
ball videos. We present two synchronization results.
The first pair of sequences, illustrated in Fig. 9(a),
shows two players seen from two cameras with almost
opposite viewpoints. In addition to the challenging
views, another difficulty of this experiment lies in the
large time-shift equal to 76 frames between both con-
sidered videos. The second pair of sequences is pre-
sented in Fig. 10(a) where four players can be seen in
both views. At some instance, some players move out
of the field of views of cameras.
For both image sequences, we synchronize de-
scriptors of the computed SSM-of. The time warp-
ing functions illustrated by the red curve in Fig. 9(c)
VIEW-INDEPENDENT VIDEO SYNCHRONIZATION FROM TEMPORAL SELF-SIMILARITIES
389

and Fig. 10(c) recover the ground truth transforma-
tions (blue curve).Thesynchronization of the first pair
of image sequences demonstrates that the method can
handle large time-shift, provided that motion in se-
quences is not periodic. In addition, we can observe
that appearances and disappearances of the players
in the second pair of videos do not disturb the time-
warping estimation.
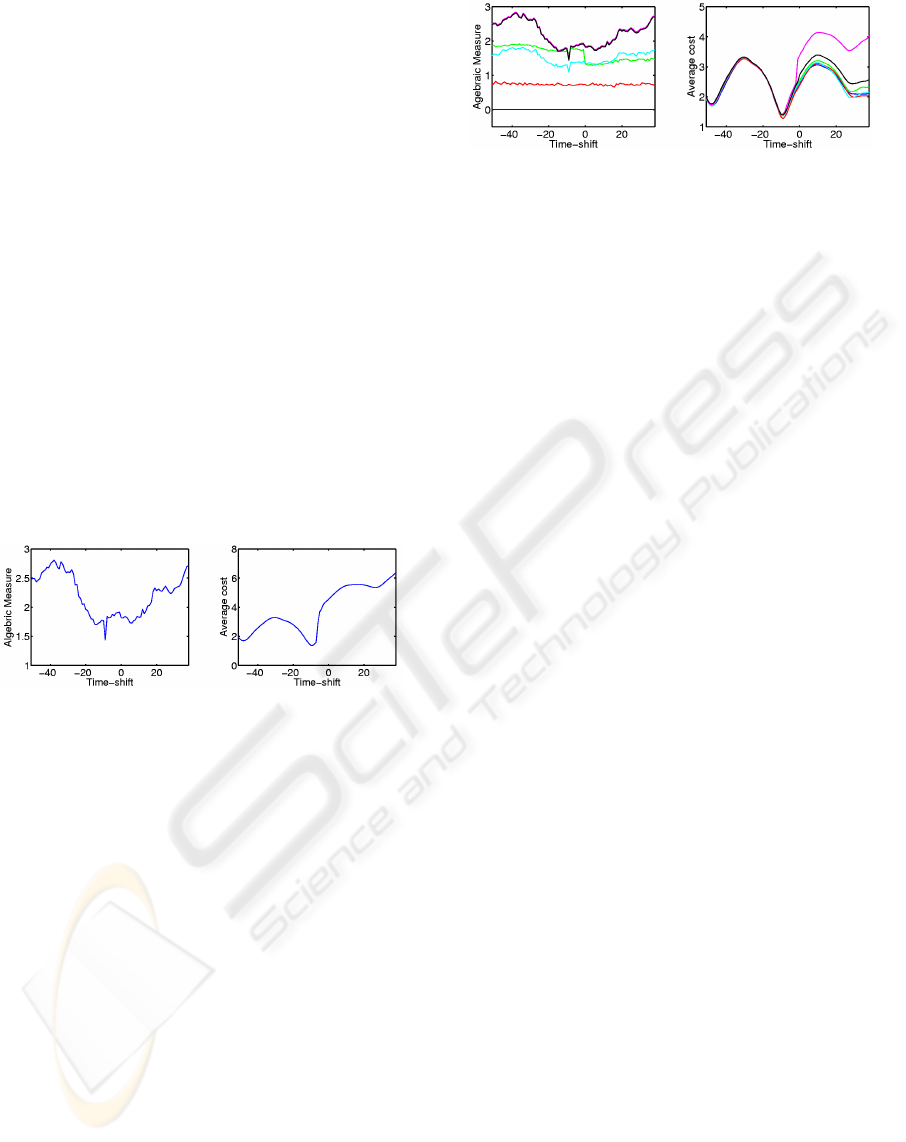
4.4 Comparison
In this subsection, we compare our method with the
approach proposed by (Wolf and Zomet, 2006)(WZ).
Due to the lack of space, we do not describe this
method and invite the reader to refer to the paper for
details. Their approach can be used to align sequences
linked by time-shift transformation. For each possi-
ble time-shift value, they evaluate an algebraic mea-
sure based on rank constraints of trajectory-based ma-
trices. They retain the time-shift that minimizes this
measure. They propose to represent results by a graph
of the computed measure versus the time-shift as il-
lustrated in Fig. 11(a).
(a) (b)
Figure 11: Results on noise-free projected MoCAP point
trajectories (a) WZ result : the algebraic error versus time-
shift (b) Our result : the average cost versus time-shift.
In order to have similar result representation, we
compute the average cost value in the cost matrix on
a path for a given time-shift. We plot this average
value versus the time-shift as illustrated in Fig. 11(b).
Fig. 11 presents results for both methods on MoCAP
dataset for the same example as in Fig. 4(e-h) but
using 20 trajectories randomly chosen for each se-
quence. We re-compute SSMs for these trajectories.
In order to compare robustness of the two ap-
proaches, we apply noises with different variances.
We can observe on Fig. 12 that for low variance noise
(black, magenta and cyan curves) both methods re-
cover the time-shift. However for higher variances,
our method can recover the time-shift whereas their
approach has difficulties (green, red and blue curves).
(a) (b)
Figure 12: Results for noisy data (a) WZ result : the alge-
braic error versus time-shift (b) Our result : the average cost
versus time-shift.
5 CONCLUSIONS
We have presented a novel approach for video syn-
chronization based on temporal self-similarities of
videos. It is characterized by its simplicity and its
flexibility: we do not impose restrictive assumptions
as sufficient background information, or point cor-
respondences between views. In addition, temporal
self-similarities, which are not strictly view-invariant,
supply view-independentdescriptors for synchroniza-
tion. Although our method does not provide syn-
chronization with sub-frame accuracy, it can perform
video synchronization automatically without tempo-
ral misalignment modeling.
We have validated our framework on datasets with
controlled view settings and tested its performance
on challenging real videos. These videos were cap-
tured by static cameras but the method could be ap-
plied to moving cameras, which we will investigate in
future work. Furthermore, as the self-similarity ma-
trix structures are not only stable under view changes
but also specific to actions, the method could address
the problem of action synchronization, i.e. the tempo-
ral alignment of sequences featuring the same action
performed by different people under different view-
points.
REFERENCES
Benabdelkader, C., Cutler, R. G., and Davis, L. S.
(2004). Gait recognition using image self-similarity.
EURASIP J. Appl. Signal Process., 2004(1):572–585.
Carceroni, R., Padua, F., Santos, G., and Kutulakos, K.
(2004). Linear sequence-to-sequence alignment. In
Proc. Conf. Comp. Vision Pattern Rec., pages I: 746–
753.
Caspi, Y. and Irani, M. (2002). Spatio-temporal alignment
of sequences. IEEE Trans. on Pattern Anal. and Ma-
chine Intell., 24(11):1409–1424.
Cha, S. and Srihari, S. (2002). On measuring the dis-
VISAPP 2009 - International Conference on Computer Vision Theory and Applications
390

tance between histograms. Pattern Recognition,
35(6):1355–1370.
Cutler, R. and Davis, L. (2000). Robust real-time periodic
motion detection, analysis, and applications. PAMI,
22(8):781–796.
Dalal, N. and Triggs, B. (2005). Histograms of oriented
gradients for human detection. In Proc. Conf. Comp.
Vision Pattern Rec, volume 2, pages 886–893.
Junejo, I., Dexter, E., Laptev, I., and P´erez, P. (2008).
Cross-view action recognition from temporal self-
similarities. In Proc. Eur. Conf. Comp. Vision, pages
293–306.
Lele, S. (1993). Euclidean distance matrix analysis (edma):
Estimation of mean form and mean form difference.
Mathematical Geology, 25(5):573–602.
Lucas, B. and Kanade, T. (1981). An iterative image regis-
tration technique with an application to stereo vision.
In Image Understanding Workshop, pages 121–130.
Rabiner, L., Rosenberg, A., and Levinson, S. (1978). Con-
siderations in dynamic time warping algorithms for
discrete word recognition. IEEE Trans. on Acoustics,
Speech and Signal Processing, 26(6):575– 582.
Rao, C.and Gritai, A., Shah, M., and Syeda Mahmood, T. F.
(2003). View-invariant alignment and matching of
video sequences. In Proc. Int. Conf. on Image Pro-
cessing, pages 939–945.
Shechtman, E. and Irani, M. (2007). Matching local self-
similarities across images and videos. In Proc. Conf.
Comp. Vision Pattern Rec.
Stein, G. (1999). Tracking from multiple view points: Self-
calibration of space and time. In Proc. Conf. Comp.
Vision Pattern Rec., volume 1, pages 521–527.
Tuytelaars, T. and Van Gool, L. (2004). Synchronizing
video sequences. In Proc. Conf. Comp. Vision Pattern
Rec., volume 1, pages 762–768.
Ukrainitz, Y. and Irani, M. (2006). Aligning sequences
and actions by minimizing space-time correlations. In
Proc. Europ. Conf. on Computer Vision.
Ushizaki, M., Okatani, T., and Deguchi, K. (2006). Video
synchronization based on co-occurrence of appear-
ance changes in video sequences. In Int. Conf. on Pat-
tern Recognition, pages III: 71–74.
Weinland, D., Boyer, E., and Ronfard, R. (2007). Action
recognition from arbitrary views using 3d exemplars.
In Proc. Int.Conf. on Computer Vision, pages 1–7.
Wolf, L. and Zomet, A. (2006). Wide baseline matching
between unsynchronized video sequences. Int. J. of
Computer Vision, 68(1):43–52.
VIEW-INDEPENDENT VIDEO SYNCHRONIZATION FROM TEMPORAL SELF-SIMILARITIES
391