
BAYESIAN SCENE SEGMENTATION INCORPORATING MOTION
CONSTRAINTS AND CATEGORY-SPECIFIC INFORMATION
Alexander Bachmann and Irina Lulcheva
Department for Measurement and Control, University of Karlsruhe (TH), 76 131 Karlsruhe, Germany
Keywords:
Stereo vision, Motion segmentation, Markov Random fields, Object classification, Global image context.
Abstract:
In this paper we address the problem of detecting objects form a moving camera by jointly considering low-
level image features and high-level object information. The proposed method partitions an image sequence
into independently moving regions with similar 3-dimensional (3D) motion and distance to the observer. In the
recognition stage category-specific information is integrated into the partitioning process. An object category
is represented by a set of descriptors expressing the local appearance of salient object parts. To account for the
geometric relationships among object parts a structural prior over part configurations is designed. This prior
structure expresses the spatial dependencies of object parts observed in a training data set. To achieve global
consistency in the recognition process, information about the scene is extracted from the entire image based
on a set of global image features. These features are used to predict the scene context of the image from which
characteristic spatial distributions and properties of an object category are derived. The scene context helps to
resolve local ambiguities and achieves locally and globally consistent image segmentation. Our expectations
on spatial continuity of objects are expressed in a Markov Random Field (MRF) model. Segmentation results
are presented based on real image sequences.
1 INTRODUCTION
One of the cornerstones in the development of auto-
motive driver assistance systems is the comprehen-
sive perception and understanding of the environment
in the vicinity of the vehicle. Especially for appli-
cations in the road traffic domain the robust and re-
liable detection of close-by traffic participants is of
major interest. In this context, vision sensors pro-
vide a rich and versatile source of information (Sivak,
1996), (Rockwell, 1972). Visual object detectors are
expected to cope with a wide range of intra-class char-
acteristics, i.e. variations in the visual appearance of
an object due to changes in orientation, lighting con-
ditions, scale, etc.. At the same time, these methods
must retain enough specificity to yield a minimum
amount of misclassifications. Here, most of the ap-
proaches developed in the last decades can be parti-
tioned into either: (i) methods based on classification
which constrain the detection process to a very spe-
cific representation of an object learned from a ref-
erence data set or (ii) methods performing object de-
tection by employing local object characteristics on
a low level of abstraction using image-based criteria
to describe coherent groups of image points as e.g.
grey level similarity, texture or motion uniformity of
image regions. A major drawback of these meth-
ods is the fact that the grouping criteria mostly ig-
nore object-specific properties with the consequence
of misdetection rates in cluttered real world scenes
that are still prohibitive for most driver assistance ap-
plications. This limitation can be weakened by clas-
sification methods that have proven to detect a large
portion of typical objects at moderate computational
cost.
In our approach object detection is performed
based on the relative motion of textured objects and
the observer. The expectation of spatial compactness
for most real world objects is expressed by its posi-
tion relative to the observer. To obtain a dense rep-
resentation of the observed scene, object detection is
formulated as an image segmentation task. Here, each
image point is tested for consistency with a set of pos-
sible hypothesis, each defined by a 3D motion and po-
sition. The set of object parameters that best explains
the measured quantities of the image point is assigned
to the image point.
To further increase the quality of the segmenta-
291
Bachmann A. and Lulcheva I. (2009).
BAYESIAN SCENE SEGMENTATION INCORPORATING MOTION CONSTRAINTS AND CATEGORY-SPECIFIC INFORMATION.
In Proceedings of the Fourth International Conference on Computer Vision Theory and Applications, pages 291-298
DOI: 10.5220/0001653302910298
Copyright
c
SciTePress
tion result, we incorporate information about the ob-
jects to be recognised by the system. The integra-
tion of object-specific information for driving image
segmentation methods has recently developed into a
field of active research and seems to be a promis-
ing way to incorporate more information into exist-
ing low-level object detection methods, see e.g. (Ohm
and Ma, 1997; Burl et al., 1998). Our work is in-
spired by recent research results in human vision,
as e.g. (Rentschler et al., 2004), indicating that the
recognition and segmentation of a scene is a heavily
interweaved process in human perception. Follow-
ing this biological model our segmentation method
is based on low-level features but guided and sup-
ported by category-specific information. The ques-
tion of how to describe this knowledge is very chal-
lenging because there is no formal definition of what
constitutes an object category. Though most people
agree on the choice of a certain object category, there
is still much discussion on the choice of an appropri-
ate object descriptor. In our approach the high-level
information comprises the appearance of a set of char-
acteristic object parts and its arrangement relative to
each other and in the scene. Though good for model-
ing local object information it fails to capture global
consistency in the recognition process, as e.g. the de-
tection of a car in a tree high above the road. We
establish global consistency by exploiting the close
relationships of certain object categories to the scene
of the image. The method characterises a scene by
global image features and derives the predicted cat-
egory likelihood and distribution of an object for a
particular scene. We argue that the incorporation of
category-specific scene context into our scene seg-
mentation framework can drastically improvethe pro-
cess as (i) insufficient intrinsic object information can
be augmented with and (ii) local ambiguities can be
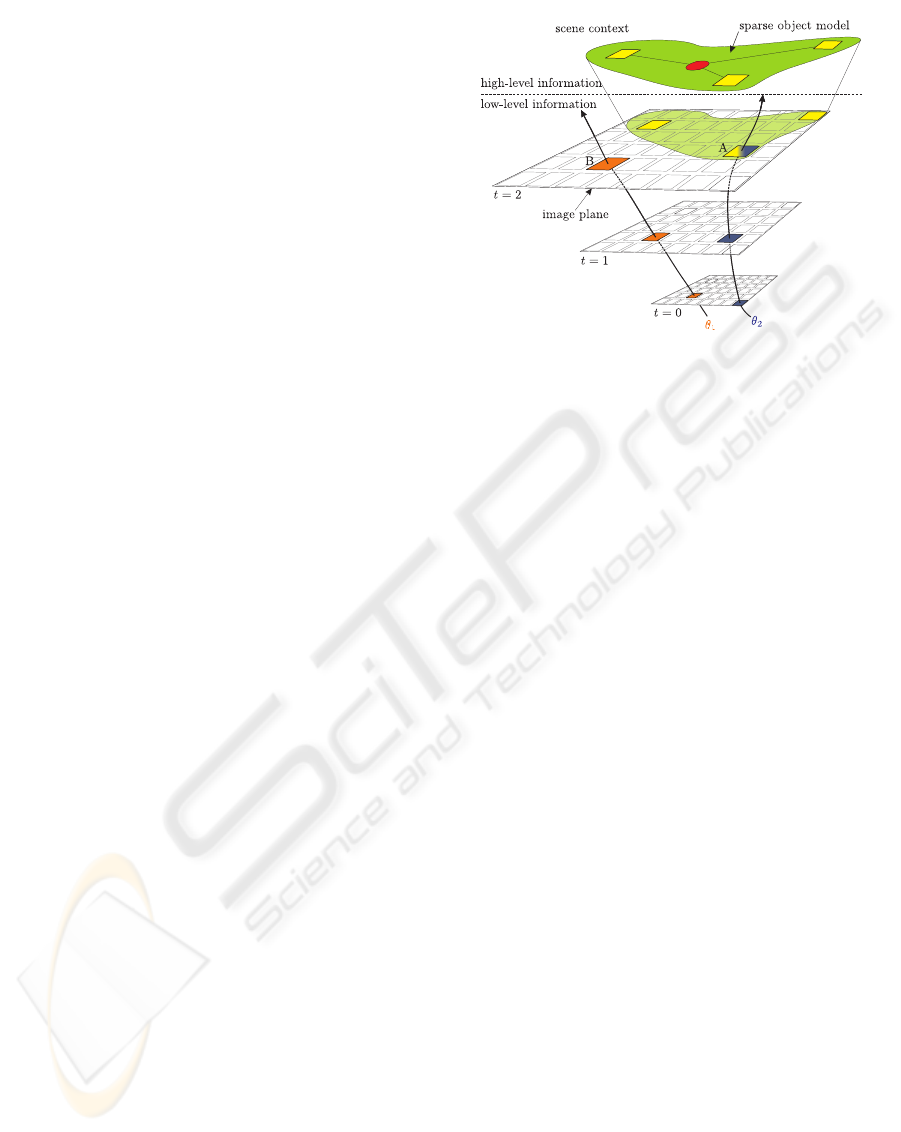
better resolved from a global perspective. Figure 1
shows the principle of our probabilistic image seg-
mentation framework.
The remainder of the paper is organised as fol-
lows. Section 2 recalls some of the theoretical back-
ground that is needed to understand image segmen-
tation as presented here. It is shown how object-
specific information can be incorporated into the ex-
isting probabilistic framework by means of a sparse
object model and category-specific scene informa-
tion. Section 3 presents the experimental results be-
fore conclusions are drawn in Section 4.
Figure 1: Principle of the combined segmentation process.
Image segmentation is performed by a Bayesian maximum
a posteriori estimator assigning the most probable object
hypothesis to each image point. In the example, image
points are assigned to either object hypothesis 1 (B, ex-
pressed by θ
1
) or object hypothesis 2 (A, expressed by θ
2
).
2 SCENE SEGMENTATION
USING MRFs
This section outlines the mechanism that evaluates the
local and global properties of image points and sepa-
rates the image accordingly. Notably there are two
issues to be addressed in this task: (i) how to encour-
age the segmentation to consider local properties in
the image on a low abstraction level and (ii) how to
enforce the process to incorporate category-specific
information into the segregation of the image.
First, a number of constraints are formulated that
specify an acceptable solution to the problem. In
computer vision, commonly the data and prior knowl-
edge are used as constraints. The data constraint re-
stricts a desired solution to be close to the observed
data and the prior constraint confines the desired solu-
tion to have a form agreeable with the a priori knowl-
edge.
The challenging task is the estimation of object
parameters θ =
θ
1
, .., θ
K
given an observation set
Y which has been generated by an unknown and con-
stantly changing number of objects K. Within our
framework we solved this by formally expressing the
scene segmentation process as labeling problem: Let
a set of sites (or units) P = {p
1
, .., p
N
} ,p
i
∈ R
2
and a
set of possible labels L be given with one label l
i
for
each site p
i
specifying the process which generated
the data. l
i
is a binary vector such that l
j
i
= 1 if object
j generated the data at site p
i
. The desired labeling
is then a mapping l : P 7→ L that assigns a unique la-
VISAPP 2009 - International Conference on Computer Vision Theory and Applications
292

bel to each site. The labeling l = (l(p
1
), .., l(p
N
)) =
(l
1
, .., l
N
) shall ascertain that (i) the data of all sites
with identical label exhibit similarity w.r.t. some mea-
sure and that (ii) the labeling conforms with the a pri-
ori knowledge.
Taking a Bayesian perspective the posterior prob-
ability of a labeling l can be formulated
P(l|Y, θ) =
P(Y|l, θ)P(l|θ)
P(Y, θ)
, (1)
where we try to find the labeling l which maximises
P(l|Y, θ). Here, P(Y|l, θ) states the data constraint
parametrised by object parameter vector θ. P(l|θ)
states the prior term. Obviously, P(Y) in Equation (1)
does not depend on the labeling l and can thus be
discarded during the maximization. By rearranging
Equation (1) the maximum a posteriori (MAP) esti-
mate of a labeling can be expressed
b
l = argmax
l
P(Y|l, θ)
| {z }
data term
P(l|θ)
|{z}
prior term
.
(2)
Assuming the observations Y to be i.i.d. normal,
the first term in Equation (2) can be written
P(Y|l, θ) =
N
∏
i=1
P(y
i
|l
i
, θ)
∝
N
∏
i=1
exp(−E
i
(y
i
|l
i
, θ)).
(3)
E
i
denotes an energy functional, rating observation y
i
given label vector l
i
and object parameter vector θ.
If there exists no prior knowledge about the val-
ues of θ (i.e. P(θ) = const.) prior expectations on l
can be modelled using MRFs. An MRF is defined
by the property P(l
i
|l
1
, .., l
i−1
, l
i+1
, l
N
) = P(l
i
|l
j
, ∀
j
∈
G
i
), with G
i
being the neighbourhood set of image
point p
i
. The system must fulfill the constraints (i)
p
i
6∈ G
i
∀l
i
, no site is its own neighbour and (ii) p
i
∈
G
j
⇔ p
j
∈ G
i
, if p
i
is a neighbour of p
j
, then p
j
is also
a neighbour of p
i
. Due to the equivalence of MRF
and Gibbs distributions, see e.g. (Besag, 1974), an
MRF may be written as P(l) =
1
Z
exp(−V
k
(l)), where
V
k
(l) ∈ R is referred to as clique potential which only
depends on those labels of l whose sites are elements
of clique k. A clique k ⊆ P is any set of sites such
that any of its pairs are neighbours. We model the
clique potential for 2-element cliques k =
p
i
, p
j
with |p
i
− p
j
| = 1 using an extension of the gener-
alised Potts model ((Geman and Geman, 1984))
V
{i, j}
(l
i
, l
j
) =
λ if l
i
6= l
j
0 otherwise
, (4)
favoring identical labels at neighbouring sites. The
coefficient λ modulates the effect of the prior term
and therefore the degree of label smoothness in the
segmentation result. The generalised Potts model is
a natural and simple way to define a clique poten-
tial function that describes the smoothness of neigh-
bouring points. With Equation (3)–(4), Equation (2)
evolves to
b
l = argmin
l
N
∑
i=1
E
i
(y
i
|l
i
, θ) +
N
∑
i=1
∑
j∈k
V
{
i, j}
(l
i
, l
j
)
=argmin
l
Ψ(E, l, θ) .
(5)
2.1 Low-level Information
Concerning the data term, in (Bachmann and Dang,
2008) excellent results have been achieved using the
property object motion. Here, objects are specified by
a 6-degree-of-freedom(dof) parametric motion model
representing the motion of an image region by pa-
rameter vector v. The similarity between expected
and observed object motion is expressed by evalu-
ating the similarity between expected image texture
G
t−1
(p
i
;r;v) derived from motion profile v and ob-
served image texture G
t
(p
i
;r) within a block of size
B centered around image point p
i
E
i
(ε
v
i
|l
i
, v) =
∑
r∈B
G
t
(p
i
;r) − G
t−1
(p
i
;r;v)
2
, (6)
with ε
v
i
stating the residual at image position p
i
.
This object model has been further extended by
the object position ξ relative to the own vehicle, i.e.
θ = (v, ξ). The relative object position is expressed
by the mean disparity ξ
∆
of all image points assigned
to the respective label and the assignment energy of
image point p
i
given an object label is
E
i
(ε
ξ
i
|l
i
, ξ) =
∆
i
− ξ
∆
2
2σ
2
ξ
∆
. (7)
σ
ξ
∆
states the extension of the object in terms of the
variance of the disparity values assigned to the object
label.
The object model presented above allows to seg-
regate an image sequence into K distinct regions with
each region being defined as homogenously moving
object at a certain distance to the observer, i.e. L =
{
background
,
object 2
, ..,
object K
}, with image
regions moving static relative to the observer (as e.g.
trees, buildings, etc.) being labeled {
background
}.
With the intention to classify every image point
into a meaningful semantic category and due to the
well-known limitations of motion-based segmenta-
tion methods (as e.g. the aperture problem or poorly
textured image regions) the next step is to incorpo-
rate category-specific information into the segmenta-
tion process.
BAYESIAN SCENE SEGMENTATION INCORPORATING MOTION CONSTRAINTS AND CATEGORY-SPECIFIC
INFORMATION
293

2.2 Category-specific Information
Therefore we extend our algorithm to perform in-
terleaved object recognition and segmentation. To
achievethis, the object parameter vector θ is extended
by model parameter Φ expressing the configuration of
an object of a certain category c
O
. An image point
is either assigned to one of the defined object cat-
egories {
car, bicycle, pedestrian
} ∈ c
O
or, if
none of the categories adequately describes the image
point, {
obstacle
} ∈ c
O
. To incorporate object cate-
gories into our segmentation scheme, Equation (5) is
extended to
Ψ(E, l, θ) = Ψ(E, l, v, ξ)
| {z }
object motion & position
+ Ψ(E, l, Φ)
| {z }
object category
,
(8)
with
Ψ(E, l, Φ) =
N
∑
i=1
E
i
(ε
Φ
i
|l
i
, Φ). (9)
The function E(ε
Φ
i
|l
i
, Φ) ascertains that image points
falling close to a given object description would more
likely carry the object category label and vice versa.
The energy functional has the form
E
i
(ε
Φ
i
|l
i
, Φ) = −log P(ε
Φ
i
|l
i
, Φ). (10)
For this work P(ε
Φ
i
|l
i
, Φ) is defined as
P(ε
Φ
i
|l
j
i
= 1, Φ) =
1
1+ d(p
i
, Φ
j
)
, (11)
with d(p
i
, Φ
j
) expressing the distance from image
point p
i
to the object that is parametrised by Φ
j
.
In this work, an object of a certain category is
characterised by the local appearance of a set of n
salient parts Φ = (φ
1
, ..., φ
n
), with φ
i
= (x
i
, y
i
, z
i
, ρ
i
)
stating the location of the i-th part in 3D space and
ρ
i
being the scale factor. Depth z
i
is obtained from
a calibrated stereo camera setup (Dang et al., 2006).
The structural arrangement of the parts comprising an
object is expressed by the spatial configuration of Φ.
Spatial relationships between parts in the sparse ob-
ject model are captured by parameter s. The local ap-
pearance of each part is characterised by parameter a.
The pair M = (s, a) parameterises an object category.
Again, using Bayes rule the probability of an object
being at a particular location, given fixed model pa-
rameters, can be written
P
M
(Φ|Y) ∝ P
M
(Y|Φ)P
M
(Φ) . (12)
Above, P
M
(Y|Φ) is the likelihood of the feature
points depicting an object for a certain configuration
of the object parts. The second term in Equation (12)
is the prior probability that the object obeys the spatial
configuration Φ. Assuming the object is present in an
image, the location that is most likely its true position
is the one with maximum posterior probability
ˆ
Φ ∝ argmax
Φ
P
M
(Y|Φ)P
M
(Φ).
(13)
Local Appearance. The image evidence P
M
(Y|Φ)
of the individual parts in the sparse object model is
modelled by its local appearance. The part appear-
ance a
i
, characterising the i-th part of a certain ob-
ject model is extracted from an image patch cen-
tered on Π(φ
i
), where Π(·) symbolises the projec-
tion of a scene point onto the image plane. The
object-characteristic appearance of each image patch
i ∈ (1, .., n) has been learned from a set of labeled
training images. In this work three types of appear-
ance measures a
i
=
a
1
i
;a
2
i
;a
3
i
have been used to de-
scribe an object:
• Texture information a
1
i
, the magnitude of each
pixel within the patch is stacked into a his-
togramm vector to express the texture.
• Shape information a
2
i
, the Euclidean distance
transform of the edge map within the patch ex-
presses the shape.
• Height information a
3
i
, the characteristic height
of φ
i
above the estimated road plane expresses the
relative location in the scene.
The resulting patch responses constitute a vector of
local identifiers for each object category. The model
parameters have been learned from a set of labeled
training images in order to generate a representative
description of the local appearance of an object cate-
gory. Prominent regions have been extracted from the
image using the Harris interest point detector (Harris
and Stephens, 1988) and a corner detector based on
curvature scale space technique as described in (He
and Yung, 2004). For object part φ
i
and observation
vector Y follows the model likelihood
P
M
(Y|Φ) =
n
∏
i=1
P
M
(Y|φ
i
). (14)
The likelihood function measures the probability of
observing Y in an image, given a particular config-
uration Φ. Intuitively, the likelihood should be high
when the appearance of the parts agree with the im-
age data at the positions they are placed, and low oth-
erwise. Figure 2 shows the sparse object model of
object category
car
.
Structural Prior. What remains is to encode the as-
sumed spatial relationships among object parts. As
VISAPP 2009 - International Conference on Computer Vision Theory and Applications
294

(a) (b) (c)
Figure 2: Sparse representation of object category
car
: (a)
front view, (b) side view, (c) rear view. The parts used in the
training stage are marked with green rectangles containing
the part-ID.
presented in (Bachmann and Dang, 2008) the assump-
tion can be made that the part locations are indepen-
dent
P
M
(Φ) =
n
∏
i=1
P
M
(φ
i
). (15)
Here, only the metric height above the estimated
road plane has been used as structural informa-
tion. Maximizing P
M
(Φ|Y) is particularly easy as
P
M
(Y|Φ)P
M
(Φ) can be solved independently for
each φ
i
. For n parts and N possible locations in the
image this can be done in O(nN) time. A major draw-
back of this method is that it encodes only weak spa-
tial information and is unable to accurately represent
objects composed of various parts.
The most obviousapproachto represent multi-part
objects is to make no independenceassumption on the
locations of different parts. Though theoretically ap-
pealing the question of how to efficiently perform in-
ference on this spatial prior is not trivial.
A balance between the inadequate independence
assumption and the strong but hard to implement
full dependency between object parts is assumed
by maintaining certain conditional independence as-
sumptions. These assumptions can be elegantly rep-
resented using an MRF where the location of part φ
i
is
independent of the values of all other parts φ
j
, j 6= i,
conditioned on the values of the neighbours G
i
of φ
i
in
an undirected graph G(Φ, E). The structural prior is
characterised by pairwise only dependencies between
parts.
Sparse Object Model. The spatial prior is modeled
as a star structured graph with the location of the ob-
ject parts being conditioned on the location of refer-
ence point φ
R
. For a better understanding φ
R
can be
interpreted as center of mass of the object. All ob-
ject parts arranged around φ
R
are independent of one
another. A similar model is also used by e.g. (Cran-
dall and Huttenlocher, 2007; Fischler and Elschlager,
1973). Let G = (Φ, E) be a star graph with central
node φ
R
. Graphical models with a star structure have
a straight forward interpretation in terms of the con-
ditional distribution
P
M
(Φ) = P(φ
R
)
n
∏
i=1
P
M
(φ
i
|φ
R
). (16)
Reference point φ
R
acts as the anchor point for all
neighbouring parts. The positions of all other parts
in the model are evaluated relative to the position of
this reference point. In this work we chose φ
R
to be
virtual, i.e. there exists no measurable quantity that
indicates the existence of the reference point itself.
We argue that this makes the model insensitive to par-
tial object occlusion and, therefore, to the absence of
reference points. P
M
(Φ) is modelled using a Mix-
ture of Gaussian (MoG). The model parameter subset
M = (s, ·), with mean µ
i,R
and covariance σ
i,R
stating
the location of φ
i
relative to the reference point φ
R
,
has been determined in a training stage.
An optimal object part configuration (see Equa-
tion (13)) can be written in terms of observing
an object at a particular spatial configuration Φ =
(φ
1
, .., φ
n
), given the observations Y in the image.
With the likelihood function of seing object part i at
position φ
i
(given by Equation (14)) and the structural
prior in Equation (16) this can be formulated as
P
M
(Φ|Y) ∝ P(φ
R
)Γ(φ
R
|Y) , (17)
where the quality of the reference point φ
R
relative to
all parts φ
i
within the object definition is written
Γ(φ
R
|Y) = max
φ
n
∏
i=1
P
M
(φ
i
|φ
R
)P
M
(Y|φ
i
). (18)
What we are interested in, is finding the best configu-
ration for all n parts of the object model relative to φ
R
.
To reduce computational costs only points are further
processed with a likelihood P
M
(Y|φ
i
) > T, where T
is the acceptance threshold for the object hypothesis
to be true. This results in a number of candidates m
for each object part i. As this is computationally in-
feasible (O(m
n
)) for large growing n we propose a
greedy search algorithm to maximise P
M
(Φ|Y) over
all possible configurations {φ
j
i
:i = 1, .., n; j = 1, .., m}
as outlined in Table1.
2.3 Context Information
The MRF presented above efficiently models local
image information consisting of low-level features
enriched by high-level category-specific information.
However, context information capturing the over-
all global consistency of the segmentation result has
been ignored so far. By introducing a set of seman-
tic categories into the segmentation process, it is now
possible to derive category-specific object character-
istics not only on a local, object-intrinsic level but
BAYESIAN SCENE SEGMENTATION INCORPORATING MOTION CONSTRAINTS AND CATEGORY-SPECIFIC
INFORMATION
295
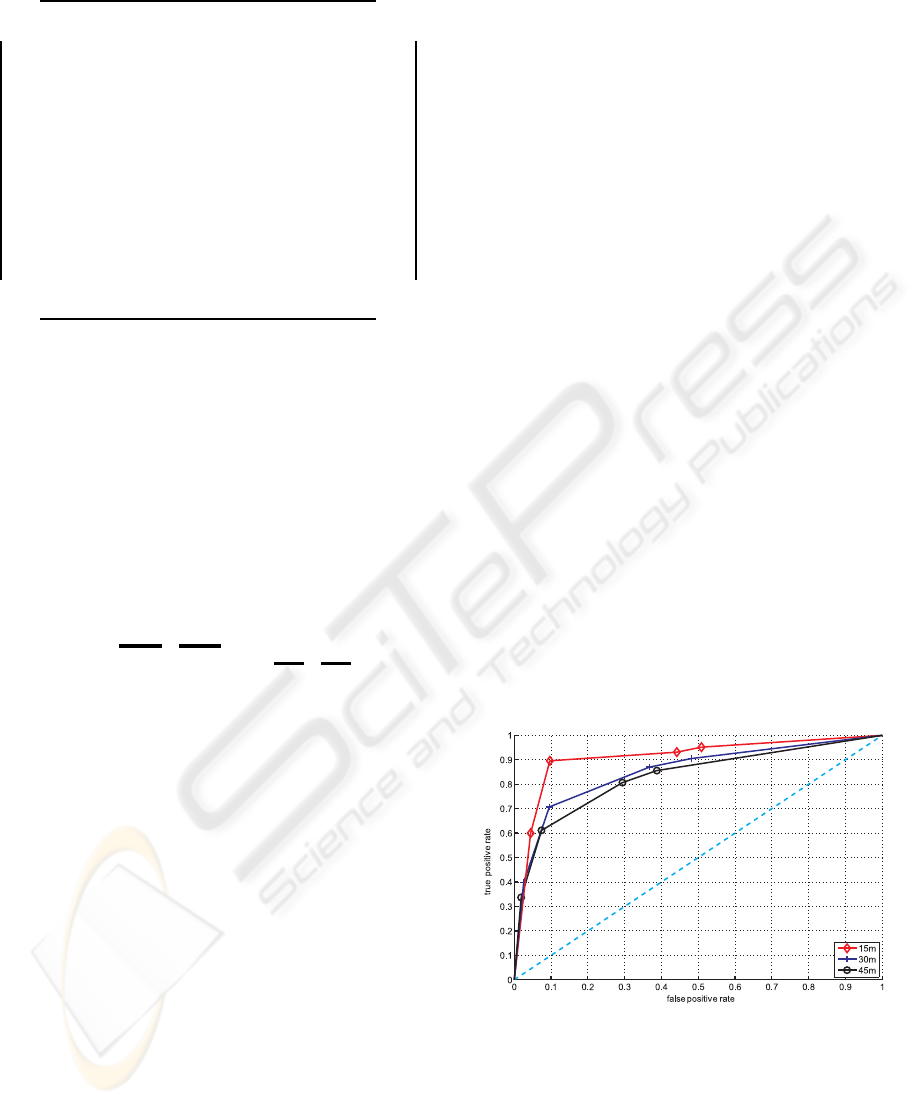
Table 1: Iterative search algorithm.
'
&
$
%
1. compute candidates φ
j
, j = (1, .., m) for
which P
M
(Y|φ
j
i
) > T
2. initialise φ
j
i
, j ∈ (1, .., m) for object part i = 1;
set k = i; for each candidate φ
j
...
(a) ...vote for reference point φ
j
R
based on part
location φ
i
(b) ...set i = i+ 1 and k = [k;i]
(c) ...back-project φ
i
from φ
j
R
and compute
P
M
(Φ
∗
|Y), with Φ
∗
= (φ
k
)
(d) ...IF P
M
(Φ
∗
|Y) > T: go back to (a);
...ELSE: end
also on a global scale, expressing the relationships be-
tween labels and global image features. In this work
this is the predicted distribution of object categories
in the image which helps to achieve globally con-
sistent recognition. Based on the work presented in
(Bachmann and Balthasar, 2008) we exploit the re-
lation between the expected distribution of a certain
category and the scenery. The scene-based informa-
tion is formally introduced into our framework by ex-
tending Equation (5) with a context-awareobject prior
predicting the distribution of category labels
Ψ(E, l, θ) = Ψ(E, l, v, ξ,Φ)
| {z }
local information
+
N
∑
i=1
G
i
(l
i
|Y)
| {z }
context information
,
(19)
with category context potential
G
i
(l
i
|Y) = logP(l
i
|M
C
) . (20)
G
i
(·) predicts the label l
i
from a global perspective
using global image features M
C
. The global features
characterise the entire image in terms of magnitude
and orientation of edges in different image resolu-
tions. For this work we defined a set of scene cate-
gories c
S
= {
open, semi-open, closed
}, each ex-
pressed by a unique feature vector M
C
, describing the
openness of the scene. This information is used to de-
rive the distribution of category labels and category
probability in the image. The feature vector M
C
for
each specific scene has been calculated from a train-
ing data set and is formally expressed by a mixture of
Gaussian model. The relationships between the con-
textual features and a specific object category c
O
has
been learned in a training stage as presented in (Bach-
mann and Balthasar, 2008). Given an input image, the
prior probability of an object category c
O
is expressed
as its marginal distribution over all scene categories c
S
whereas the scene similarity of the input image (ex-
pressed by M
obs
C
) to the defined scene categories is
determined by calculating the joint probability with
the single components in M
C
.
3 EXPERIMENTAL RESULTS
This section presents the experimental evaluation of
the object detection approach developed in the pre-
vious sections. The results are based on image se-
quences of typical urban traffic scenarios. The al-
gorithm is initialised automatically by scanning for
the actual number of dominant motions in the scene.
Concerning the motion of the observer, the road plane
is determined at the beginning of the image sequence
as described in (Duchow et al., 2006). Thus, the mo-
tion profile of the observer can be determined by sam-
pling feature points exclusively from the region that
is labeled as road plane and therefore static relative
to the observer. During the segmentation process, the
motion profiles are refined and updated continuously
with the motion tracker scheme described in (Bach-
mann and Dang, 2008). Regarding the relative im-
portance of data and smoothness term in the segmen-
tation process, the regularization factor was adapted
empirically to values between λ = (0.05, .., 0.5).
The confidence of an image point to be part of
an object hypothesis, i.e. label, is calculated based
on its relative motion, its position and similarity to
the defined object categories. The image point is as-
signed to the label with highest confidence. The train-
ing data for object category
car
as presented here was
extracted from an image data base of 160 images.
Figure 3: ROC-curve for rear view of object category
car
as a function of the distance from the observer.
Figure 3 shows that a threshold value of T ≈ 0.6
yields a good compromise between a reasonable true
positive rate and a false positive rate at relative low
values.
Figure 4 shows some of the detection results for
object category
car
. The model was learned from
VISAPP 2009 - International Conference on Computer Vision Theory and Applications
296

labeled data. The patch-size of the extracted inter-
est points was scale-normalised based on a predefined
reference scale.
Figure 4: Detection results (threshold value T = 0.5) for
object category
car
. The figure on the bottom right shows
a false positive.
Figure 5 shows the classification results for de-
tected objects solely based on scene context. No lo-
cal category information has been integrated. It can
be seen that the integration of global information is
useful as a first process of image recognition. Joint
use of the proposed local object detector together with
category-specific scene context improves the recogni-
tion accuracy as shown in Figure 6.
Figure 5: Left: Detected objects based on the local ob-
ject properties motion similarity and position. Right: Prior
probability P
M
C
(l
S
i
= O) of image region S
i
to belong to ob-
ject category O = {
car, bicycle, pedestrian
} solely
based on scene context information.
Here, the object detection and segmentation re-
sults for different traffic scenes is depicted. As in this
work only object category
car
is known locally to the
system, detected objects that are labeled
bicyclist
or
pedestrian
rely solely on the global context of the
image. In the initialization phase of the segmentation
process the motion estimates for the labels are inac-
curate. Therefore the segmentation is mainly driven
by the appearance-based confidence measure. With
increasing accuracy and distinctiveness of the labels
motion profile, the influence of the motion cue in-
creases. In most cases, it takes less than 3 frames to
partition the image into meaningful regions.
4 CONCLUSIONS
This paper has presented a MRF for pixel-accurate
object recognition that models local object informa-
tion and global information explicitly. The local in-
formation consists of a set of distinct 6-dof motion
profiles, positions and - on a high abstraction level
- the local appearance similarity to the trained ob-
ject category
car
. Distinctive, local object descriptors
and a structural prior on the object-parts configuration
have been extracted from a set of sample images. The
structural relationships among object parts has been
modelled as sparse structural prior. Object recogni-
tion is realised by an iterative method that finds an
optimal configuration of the object parts based on the
local appearance in the image and its spatial arrange-
ment. Global information is derived from scene-based
information generated according to the scene of the
input image. As the occurrence of object categories is
closely related to the scene of the image, scene con-
text is exploited to derive characteristic category dis-
tributions and probabilities. It has been shown that
the joint use of a local object detector and scene con-
text improves the recognition accuracy. Under the as-
sumption of motion and category homogeneity within
the boundaries of an object, spatial consistency has
been modelled through a Markov Random Field.
In ongoing work, we expect to increase the perfor-
mance of the method by further refining and extend-
ing the sparse object model description. We suppose
to increase the quality of the classification process by
making the object appearance descriptors invariant to
object orientation and rotation. Additionally, the per-
formance shall be increased by an exhausting train-
ing of different object categories. Furthermore it is
intended to speed up the search algorithm that incor-
porates the object spatial configuration to make the
entire process computationally feasible.
ACKNOWLEDGEMENTS
This work was partly supported by the Deutsche
Forschungsgemeinschaft DFG within the collabora-
tive research center ‘Cognitive Automobiles’.
REFERENCES
Bachmann, A. and Balthasar, M. (2008). Context-aware ob-
ject priors. In IEEE IROS 2008; Workshop on Plan-
ning, Perception and Navigation for Intelligent Vehi-
cles (PPNIV), Nice, France.
BAYESIAN SCENE SEGMENTATION INCORPORATING MOTION CONSTRAINTS AND CATEGORY-SPECIFIC
INFORMATION
297

Figure 6: Left: Scenes with a variable number of moving objects. The 6–dof motion for each object is determined based
on a set of interest points extracted from the respective object. Coloured markers indicate the tracked points. Middle: The
resulting segmentation map. Each image point is assigned the label containing the most probable motion profile and position.
Right: The segmented image. Image points assigned to an object label are highlighted.
Bachmann, A. and Dang, T. (2008). Improving motion-
based object detection by incorporating object-
specific knowledge. International Journal of Intel-
ligent Information and Database Systems (IJIIDS),
2(2):258–276.
Besag, J. (1974). Spatial interaction and the statistical anal-
ysis of lattice systems. Journal of the Royal Statistical
Society, Series B 36(2):192–236.
Burl, M. C., Weber, M., and Perona, P. (1998). A probabilis-
tic approach to object recognition using local photom-
etry and global geometry. Lecture Notes in Computer
Science, 1407:628ff.
Crandall, D. and Huttenlocher, D. (2007). Composite mod-
els of objects and scenes for category recognition. In
Proc. IEEE Conference on Computer Vision and Pat-
tern Recognition CVPR ’07, pages 1–8.
Dang, T., Hoffmann, C., and Stiller, C. (2006). Self-
calibration for active automotive stereo vision. In Pro-
ceedings of the IEEE Intelligent Vehicles Symposium,
Tokyo.
Duchow, C., Hummel, B., Bachmann, A., Yang, Z., and
Stiller, C. (2006). Akquisition, Repraesentation und
Nutzung von Wissen in der Fahrerassistenz. In In-
formationsfusion in der Mess- und Regelungstechnik
2006, VDI/VDE-GMA. Eisenach, Germany.
Fischler, M. and Elschlager, R. (1973). The representa-
tion and matching of pictorial structures. IEEE Trans.
Comput., 22(1):67–92.
Geman, S. and Geman, D. (1984). Stochstic relaxation,
Gibbs distribution, and the Bayesian restoration of im-
ages. In IEEE Transaction on Pattern Analysis and
Machine Intelligence, volume 6, pages 721–741.
Harris, C. and Stephens, M. (1988). A combined corner
and edge detector. In Fourth Alvey Vision Conference,
Manchester, pages 147–151.
He, X. and Yung, N. (2004). Curvature scale space corner
detector with adaptive threshold and dynamic region
of support. In 17th International Conference on Pat-
tern Recognition, volume 2, pages 791–794, Washing-
ton, DC, USA. IEEE Computer Society.
Ohm, J.-R. and Ma, P. (1997). Feature-Based cluster seg-
mentation of image sequences. In ICIP ’97-Volume 3,
pages 178–181, Washington, DC, USA. IEEE Com-
puter Society.
Rentschler, I., Juettner, M., Osmana, E., Mueller, A., and
Caell, T. (2004). Development of configural 3D object
recognition. Elsevier - Behavioural Brain Research,
149(149):107–111.
Rockwell, T. (1972). Skills, judgment, and information ac-
quisition in driving. Human Factors in Highway Traf-
fic Safety Research, pages 133–164.
Sivak, M. (1996). The information that drivers use: is it
indeed 90% visual? Perception, 25(9):1081–1089.
VISAPP 2009 - International Conference on Computer Vision Theory and Applications
298
