RELATING KNOWLEDGE SPECIFICATIONS

BY REDUCTION MAPPINGS

Alexei Sharpanskykh and Jan Treur

Vrije Universiteit Amsterdam, De Boelelaan 1081a, Amsterdam, The Netherlands

Keywords: Reduction relations, Automated mapping of specifications, Cognitive science.

Abstract: Knowledge can be specified at different levels of conceptualisation or abstraction. In this paper, lessons

learned on the philosophical foundations of cognitive science are discussed, with a focus on how the

relationships of cognitive theories with specific underlying (physical/biological) makeups can be dealt with.

It is discussed how these results can be applied to relate different types of knowledge specifications. More

specifically, it is shown how different knowledge specifications can be related by means of reduction

relations, similar to how specifications of cognitive theories can be related to specifications within physical

or biological contexts. By the example of a specific reduction approach, it is shown how the process of

reduction can be automated, including mapping of specifications of different types and checking the

fulfilment of reduction conditions.

1 INTRODUCTION

Specification languages play a major role in the

development of knowledge models, as a means to

describe specific functionalities aimed at.

Functionalities can be described at different levels of

conceptualisation and abstraction, and often

different languages are available to specify them,

varying from symbolic, logical languages to

algorithmic, numerical languages. The question in

how far such different types of specifications can be

related to each other has not a straightforward

general answer yet. Specifications of different types

can just be used without explicitly relating them, as

part of a heterogeneous specification. In a particular

case relationships can be defined of the type that

output of one functionality specification is related to

input for another specification. However, it may be

useful when general methods are available to relate

the contents of different specifications as well. The

aim of this paper is to explore possibilities for such

general methods, inspired by recent work in the

philosophical foundations of Cognitive Science.

Within the philosophical literature the position of

Cognitive Science has often been debated; e.g.,

(Bennet and Hacker, 2003). Recent developments

have provided more insight in the specific

characteristics of Cognitive Science, and how it

relates to other sciences. A main issue that had to be

clarified is the role of the specific (physical or

biological) makeup of individuals (or species) in

Cognitive Science. Cognitive theories have a

nontrivial dependence on the context(s) of these

specific makeups. Due to this context-dependency,

for example, regularities or relationships between

cognitive states are not considered genuine universal

laws and cannot be directly related to general

physical or biological laws, as they simply can be

refuted by considering a different makeup. The

classical approaches to reduction that provide means

to relate properties (or laws) of one level of

conceptualization to properties (or laws) of another

level (e.g., bridge law reduction (Nagel, 1961),

functional reduction (Kim, 2005) and interpretation

mappings (Tarski et al, 1953) do not address this

context-dependency properly. In this paper a

context-dependent refinement of these approaches is

proposed that provides a way to clarify in which

sense regularities in a cognitive theory relate on the

one hand to general physical/biological laws and on

the other hand to specific makeups or mechanisms.

In this paper, first the lessons learned about the

philosophical foundations of Cognitive Science are

briefly summarised in Section 2. Section 3 shows

how these findings can be applied to relate different

knowledge specifications. This is illustrated for an

example of adaptive functionality, for which two

different types of knowledge specifications are

given: one logical specification, and one

Sharpanskykh A. and Treur J. (2009).

RELATING KNOWLEDGE SPECIFICATIONS BY REDUCTION MAPPINGS .

In Proceedings of the International Conference on Agents and Artiﬁcial Intelligence, pages 29-36

DOI: 10.5220/0001654300290036

 SciTePress

algorithmic, numerical specification. Section 4

describes how different types of reduction relations

can be defined to relate the two types of knowledge

specification. Furthermore, in Section 5 it is shown

in this example how the interpretation mapping

approach to reduction can be automated, including

checking the fulfilment of reduction conditions. The

paper concludes with a discussion in Section 6.

2 SOME OF THE MAIN ISSUES

The status of Cognitive Science has since long been

the subject of debate within the philosophical

literature; e.g. (Bickle, 1998; Kim, 1996; Kim,

2005). Among the issues questioned are the

existence and status of higher-level cognitive laws,

and the connection of a higher-level specification to

reality. Within the philosophical literature on

reduction since a long time much effort has been

invested to address these issues, with partial success;

e.g., (Nagel, 1961). In response to the severe

criticisms, alternative views have been explored.

In recent years much attention has been paid to

explore the possibilities of the notion of mechanism

within Philosophy of Science; e.g., (Craver, 2001;

Glennan, 1996). One of the issues addressed by

mechanisms is how a certain (higher-level)

capability is realised by organised (lower-level)

operations. This paper shows how certain aspects

addressed by mechanisms can also be addressed by

refinements of approaches to reduction, such as the

bridge law approach, the functional approach, and

the interpretation mapping approach.

Before going into the details, first some of the

central claims from the literature in Philosophy of

Mind are illustrated for an example case study:

(a) Cognitive laws are not genuine laws but depend on

circumstances, for example, in the form of an

organism’s makeup.

(b) Cognitive laws can not be related (in a truth-

preserving manner) to physical or biological laws.

reality in a principled manner, but, if at all, in

different manners depending on circumstances.

A central issue in these claims is the observation

that the relationship between a higher-level

conceptualisation and reality has a dependency on

the context of the physical or biological makeup of

individuals and species, and this dependency

remains unaddressed and hidden in the classical

reduction approaches. Perhaps one of the success

factors of the approaches based on mechanisms is

that referring to a mechanism can be viewed as a

way to make this context-dependency explicit.

To get more insight in the issue, an example case

study is used concerning functionality for adaptive

behaviour, as occurs, in conditioning processes in

the sea hare Aplysia. For Aplysia underlying neural

mechanisms of learning are well understood, based

on long term changes in the synapses between

neurons; see, for example, (Gleitman, 2004). Aplysia

is able to learn based on the (co)occurrence of

certain stimuli; for example; see (Gleitman, 2004).

The example functionality for adaptive

behaviour is described from a global external

viewpoint as follows. Before a learning phase a tail

shock leads to a response (contraction), but a light

touch on its siphon is insufficient to trigger such a

response. Suppose a training period with the

following protocol is undertaken: in each trial the

subject is touched lightly on its siphon and then

immediately shocked on its tail. After a number of

trials the behaviour has changed: the subject also

shows a response (contraction) to a siphon touch.

From an external viewpoint, the overall behaviour

can be summarised by the specification of a

relationship between stimuli and (re)actions

involving a number of time points:

If a number of times a siphon touch occurs, immediately

followed by a tail shock, and after that a siphon touch

occurs, then contraction will take place.

To obtain a higher-level description of the

functionality of this adaptive behaviour, a sensitivity

state for stimulus-action pairs s-a is assumed that

can have levels low, medium and high, where high

sensitivity entails that stimulus s results in action a,

and lower sensitivities do not entail this response:

If s-a sensitivity is high and stimulus s occurs, then

action a occurs.

If stimulus stim1 and stimulus stim2 occur and stim1-a

sensitivity is high, and stim2-a sensitivity is not high,

then stim2-a sensitivity becomes one level higher.

As a next step, it is considered how the mechanism

behind the higher-level description works at the

biological level for Aplysia.

The internal neural

mechanism for Aplysia’s conditioning can be

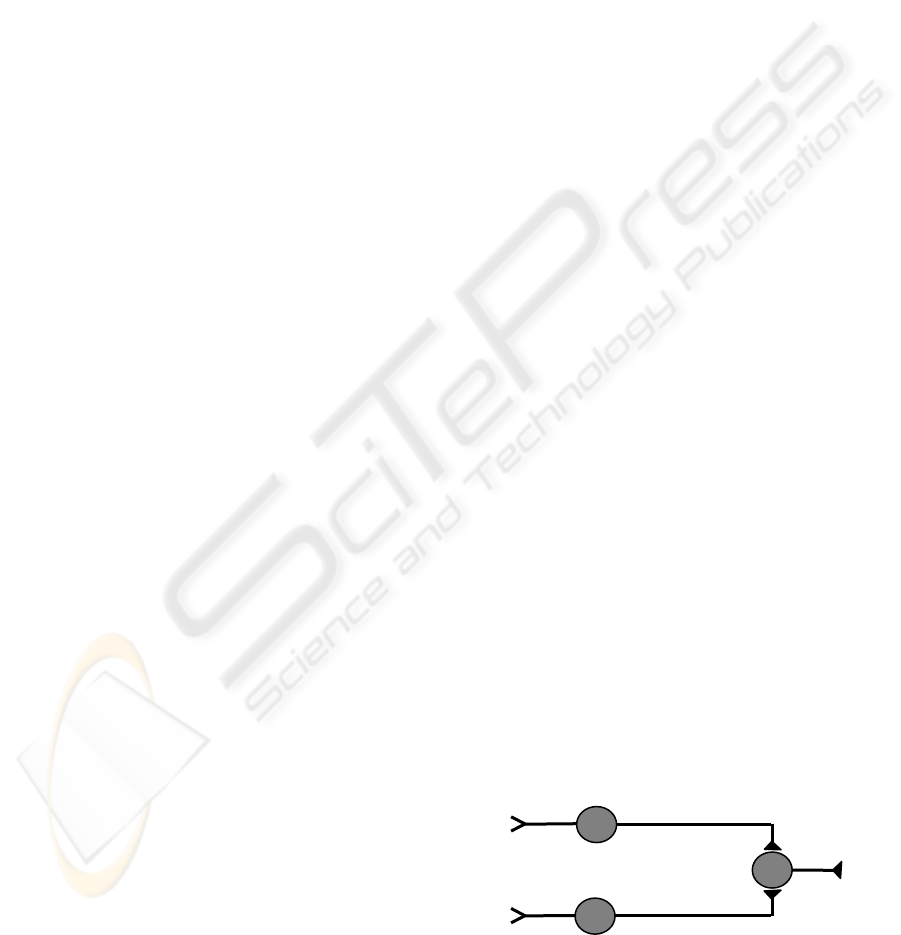
depicted as in Fig. 1, following (Gleitman, 2004).

Figure 1: A neural mechanism for adaptive functionality.

siphon

touch

tail

shock

contraction

SN2

SN1

ICAART 2009 - International Conference on Agents and Artificial Intelligence

A tail shock activates a sensory neuron SN1.

Activation of SN1 activates the motoneuron MN via

the synapse S1; activation of MN makes the sea

hare move. A siphon touch activates the sensory

neuron SN2. Activation of SN2 normally is not

sufficient to activate MN, as the synapse S2 is not

strong enough. After learning, the synapse S2 has

become stronger and activation of SN2 is sufficient

to activate MN. During the learning SN2 and MN

are activated simultaneously, and the strength of the

synapse S2 increases. This description is on the one

hand based on the specific makeup of Aplysia’s

neural system, but on the other hand makes use of

general neurological laws. A (simple) neurological

theory consisting of the following laws explains the

mechanism:

Activations of neurons propagate through

connections via synapses with high strength.

Simultaneous activation of two connected neurons

increases the strength of the synapse connecting them.

When an external stimulus occurs that is connected to a

neuron, then this neuron will be activated. When a

neuron is activated that is connected to an external

action, then this action will occur.

Claims (a) and (b) discussed above are illustrated

by the Aplysia case as follows. The neurological

laws considered

are general laws, independent of any

specific makeup; they are (assumed to be) valid for

any neural system. In contrast, the validity of the

higher-level specification not only depends on these

laws but also on the makeup of the specific type of

neural system; for example, if some of the

connections of Aplysia’s neural system are absent

(or wired differently), then the higher-level

specification will not be valid for this organism. As

the neurological laws do not depend on this makeup,

the higher-level specification can not be related (in a

truth-preserving manner) to the neurological laws.

Claim (c) can be illustrated by considering other

species than Aplysia as well, with different neural

makeup, but showing similar conditioning processes.

A central issue shown in this illustration of the

claims is the notion of makeup, which provides a

specific context of realisation of the higher-level

specification. Indeed, the classical approaches to

reduction ignore this aspect, whereas the approaches

based on the notion of mechanism explicitly address

it. However, variants of these classical approaches

can be defined that also explicitly take into account

this aspect of context-dependency, and thus provide

support for the claims (a) to (c) instead of ignoring

them. This will be addressed in Section 3.

3 CONTEXT-DEPENDENT

REDUCTION RELATIONS

Reduction addresses relationships between

descriptions of two different levels, usually indicated

by a higher-level theory T

(e.g., a cognitive theory)

and a lower-level or base theory T

(e.g., a

neurological theory). A specific reduction approach

provides a particular reduction relation: a way in

which each higher-level property or law a (an

expression in T

) can be related to a lower-level

property or law b (an expression in T

), this b is

often called a realiser for a. Reduction approaches

differ in how these relations are defined. Within the

traditional philosophical literature on reduction,

three approaches play a central role. In the classical

approach, following Nagel (1961) reduction

relations are based on (biconditional) bridge

principles a ↔ b that relate the expressions a in the

language of a higher-level theory T

to expressions b

in the language of the lower-level or base theory T

In contrast to Nagel’s bridge law reduction,

functional reduction (e.g., (Kim, 2005)) is based on

functionalisation of a state property a in terms of its

causal task C, and relating it to a state property b in

performing this causal task C. From the logical

perspective two closely related notions to formalise

reduction relations are (relative) interpretation

mappings (e.g., (Schoenfield, 1967; Kreisel, 1955).

These approaches relate the two theories T

and T

based on a mapping

relating the expressions a of

to expressions b of T

, by defining b =

(a).

Within philosophical literature, for example, Bickle

(1998) discusses a variant of the interpretation

mapping approach with roots in (Hooker, 1981).

For each of the three approaches to reduction as

mentioned a context-dependent variant will be

defined. As a source of inspiration (Kim, 1996) is

used, where it is briefly sketched how a local or

structure-restricted form of bridge law reduction can

handle multiple realisation within different

makeups. This section shows how this idea of

context-dependent reduction can be worked out for

each of three approaches, thus obtaining variants

making the dependency on a specific makeup.

In context-dependent reduction the aim is to

identify multiple context-specific sets of realisers.

When contexts are defined in a sufficiently fine-

grained manner, within one context the set of

realisers can be taken to be unique. The contexts

may be chosen in such a manner that all situations

in which a specific type of realisation occurs are

grouped together and described by this context. In

Cognitive Science such a grouping could be based

RELATING KNOWLEDGE SPECIFICATIONS BY REDUCTION MAPPINGS

on species. When within each context one unique

set of realisers exists, from an abstract viewpoint

contexts can be seen as a form of parameterisation

of the different possible sets of realisers.

In context-dependent reduction approaches, a

context can be taken a description S (of an organism

or system with a certain structure) by a set of

statements within the language of the lower-level

theory

. For a given context S as a parameter, for

each expression of

there exists a realiser within

the language of

. Context-dependent reduction as

sketched by Kim ((1996), pp. 233-236), assumes

that the contexts all are specified within the same

base theory

. However, if mental state properties

(for example, having certain sensory

representations) are assumed that can be shared

between, for example, biological organisms and

robot-like architectures, it may be useful to allow

contexts that are described within different base

theories. In the multi-theory-based multi-context

reduction approach developed below, a collection of

lower-level theories T

is assumed, and for each

theory

T in T

a set of contexts C

, such that each

organism or system is described by a specific theory

T in T

together with a specific context or makeup S

in C

; these contexts S are assumed to be

descriptions in the language of

T and consistent with

T. For the case that within one context only one

realisation is possible, the theories

T in T

and

contexts

S in C

can be used to parameterise the

different sets of realisers that are possible. Below it

is shown how contexts can be incorporated in the

three reduction approaches discussed above.

Context-dependent Bridge Law Reduction. For

this approach, a unique set of realisers is assumed

within each context S for a theory T in T

; this is

expressed by context-dependent biconditional

bridge laws. Such context-dependent bridge laws

are parameterised by the theory T in T

and context

S in C

, and can be specified by

↔ b

1,T,S

, …, a

↔ b

k,T,S

Here a

is an expression specified in the language

of theory

, and b

is an expression in the language

of theory

corresponding to a

. Given such a

parameterised specification, the criterion of context-

dependent bridge law reduction for a law

L(a

, …, a

)

of T

can be formulated (in two equivalent manners)

by:

(i) T

|─ L(a

, …, a

)

⇒

∀T∈ T

∀S∈ C

T ∪ S ∪ {a

↔ b

1,T,S

, …, a

↔ b

k,T,S

}

|─ L(a

, …, a

)

(ii) T

|─ L(a

, …, a

)

⇒

∀T∈T

∀S∈ C

T ∪ S

|─

L(b

1,T,S

, …, b

k,T,S

)

Here T |─ A denotes that A is derivable in T. Note

that this notion of context-dependent bridge law

reduction implies unique realisers (up to

equivalence) per context: from

a ↔ b

T,S

and a ↔ b'

T,S

it follows that b

T,S

↔ b'

T,S

. So the idea is that to

obtain context-dependent bridge law reduction in

cases of multiple realisation, the contexts are

defined with such a fine grain-size that within one

context unique realisers exist.

Context-dependent Functional Reduction. For a

given collection of context theories T

and sets of

contexts C

, for context-dependent functional

reduction a first criterion is that a joint causal role

specification C(P

, …, P

) can be identified such

that it covers all relevant state properties of theory

. As an example, consider the case discussed in

((Kim, 1996), pp. 105-107). Here the joint causal

role specification C(alert, pain, distress) for three

related mental state properties is described by:

For any x,

if x suffers tissue damage and is normally alert, x is in

pain

if x is awake, x tends to be normally alert

if x is in pain, x winces and groans and goes into a state

of distress

if x is not normally alert or is in distress, x tends to

make typing errors

By a Ramseification process the following joint

causal role specification is obtained. There exist

properties

, P

such that C(P

, P

) holds,

where

C(P

, P

) is

For any x,

if x suffers tissue damage and has P

, x has P

if x is awake, x has P

if x has P

, x winces and groans and has P

if x has not P

or has P

, x tends to make typing errors

The state property ‘being in pain’ of an organism is

formulated in a functional manner as follows:

There exist properties P

, P

such that C(P

, P

)

holds and the organism has property

Similarly, ‘being alert’ is formulated as:

There exist properties P

, P

such that C(P

, P

)

holds and the organism has property

A first criterion for context-dependent functional

reduction is that for each theory

T in T

and context

S in C

at least one instantiation of it within T

exists:

∀T∈T

∀S∈C

∃P

, …, P

T ∪ S

|─ C(P

, …, P

The second criterion for context-dependent

functional reduction, concerning laws or regularities

L is

|─ L(a

, …, a

)

⇒ ∀T∈

∀S∈C

∀P

, …, P

[ T ∪ S |─ C(P

, …, P

)

⇒

T ∪ S |─ L(P

, …, P

) ]

ICAART 2009 - International Conference on Agents and Artificial Intelligence

In general this notion of context-dependent

functional reduction may still allow multiple

realisation within one theory and context. However,

by choosing contexts with an appropriate grain-size

it can be achieved that within one given theory and

context unique realisation occurs. This can be done

by imposing the following additional criterion

expressing that for each

T in T

and context S in C

there exists a unique set of instantiations

(parameterised by

T and S) realising the joint causal

role specification C(P

, …, P

∀T∈ T

∀S∈C

∃P

, …, P

[ T ∪ S |─ C(P

, …, P

) &

∀Q

, …, Q

[ T ∪ S |─ C(Q

, …, Q

)

⇒ T ∪ S |─ P

↔ Q

& … & P

↔ Q

] ]

This unique realisation criterion guarantees that

for all systems with theory

T and context S any basic

state property in

has a unique realiser,

parameterised by theory

T in T

and context S in C

When also this third criterion is satisfied, a form of

reduction is obtained that we call strict context-

dependent functional reduction. Based on the unique

realisation criterion, the universally quantified form

for relations between laws is equivalent to the

following existentially quantified variant:

|─ L(a

, …, a

) ⇒

∀T∈

∀S∈C

∃P

, …, P

[T ∪ S |─ C(P

, …, P

) &

T ∪ S |─ L(P

, …, P

) ]

Context-dependent Interpretation Mappings. To

obtain a form of context-dependent interpretation,

the notion of interpretation mapping can be

generalised to a multi-mapping, parameterised by

contexts. A context-dependent interpretation of a

theory

in a collection of theories T

with sets of

contexts C

specifies for each theory T in T

and

context S in C

an appropriate mapping ϕ

T,S

from the

expressions of

to expressions of T. When both the

higher and lower level theories are specified using a

sorted predicate language, then such a multi-

mapping can be defined on the basis of mappings of

each predicate symbol from the language of

and

of its arguments – terms of the language of

– to

formulae in the language of

. Mappings of sorts,

constants, variables and functions may be specified

to define mappings of terms. Mappings of

composite formulae in the language of

are

defined as follows:

T,S

& A

) = ϕ

T,S

) & ϕ

T,S

)

T,S

(¬ A) = ¬ ϕ

T,S

(A)

T,S

(∃x. A) = ∃ϕ

T,S

(x) ϕ

T,S

(A)

Here A, A

and A

are formulae in the language of T

A multi-mapping

T,S

is a context-dependent

interpretation mapping when it satisfies the property

that if a law (or regularity)

L can be derived from T

then for each

T in T

and context S in C

the

corresponding

T,S

(L) can be derived from T ∪ S:

|─

⇒ ∀T∈T

∀S∈C

T ∪ S

|─ ϕ

T,S

(L)

Note that also here within one theory

T in T

and context

S in C

multiple realisation is still

possible, expressed as the existence of two

essentially different interpretation mappings

T,S

and

ϕ'

T,S

, i.e., such that it does not always hold that ϕ

T,S

(a)

↔ ϕ'

T,S

(a). An additional criterion to obtain unique

realisation per context is: when for a given theory T

in T

and context S in C

two interpretation

mappings

T,S

and ϕ'

T,S

are given, then for all

formulae

a in the language of T

it holds that

T ∪ S

|─ ϕ

T,S

(a) ↔ ϕ'

T,S

(a)

When for each theory and context this additional

criterion is satisfied as well, the interpretation is

called a strict context-dependent interpretation.

4 CASE STUDY

In this section the applicability of the context-

dependent reduction approaches described in Section

3 is illustrated for a case study involving adaptive

functionality inspired by the conditioning processes

in Aplysia (see Section 2).

To formalise both the lower and higher level

theories the reified temporal predicate language

RTPL (Galton, 2006) was used, a many-sorted

temporal predicate logic language that allows

reasoning about the dynamics of a system. To

express state properties (the sort

STATPROP) of a

system ontologies are used. To represent dynamics

of a system sort

TIME (a set of time points) and the

ordering relation

> : TIME x TIME are introduced in

RTPL. To indicate that some state property holds at

some time point the relation

at: STATPROP x TIME is

introduced. The terms of RTPL are constructed by

induction in a standard way. The set of well-formed

RTPL formulae is defined inductively in a standard

way using Boolean connectives and quantifiers.

In the following a specification of the higher-

level model HM for conditioning (as in Aplysia) is

provided formalised in RTPL using the state

ontology from Table 1.

In the following formalization

a and s are variable

names.

HMP1 Action performance

For any time point, if the sensitivity of a relation s-a is

high and the stimulus s is observed,

then at some later time point action a will be performed.

Formally:

RELATING KNOWLEDGE SPECIFICATIONS BY REDUCTION MAPPINGS

∀t1:TIME [ at(sensitivity(s, a, high) ∧ observesstimulus(s),

t1) ⇒ ∃t2:TIME t2 > t1 & at(performsaction(a), t2) ]

Table 1: State ontology for the higher-level model HM.

Sort Elements

STIMULUS stim1, stim2

ACTION contraction

DEGREE low, medium, high

Predicate Description

sensitivity: STIMULUS x

ACTION x DEGREE

Describes the sensitivity degree

of a stimulus-action relation

observesstimulus:

STIMULUS

Describes the observation of a

stimulus

performsaction: ACTION

Describes an action being

performed

HMP2 Sensitivity increase

For any time points t1 and t2, such that t1+1 < t2 ≤ t1+c5+1

if stimulus

stim1 is observed at t1 and the sensitivity of

relation

stim1-a is high and stimulus stim2 is observed at t2

and the sensitivity of relation

stim2-a is v, and v’ is the

value-successor of

then at

t2+2 the sensitivity of relation stim2-a will become

v’.

HMP3 Unconditional persistency of the high sensitivity

value

HMP4 Conditional persistency of the sensitivity value other

than high

For any time point t5,

if the sensitivity value of the relation

stim2-a is v≠high and

and not

stimulus

stim2 was observed at time point t5-1,

and there exists time point

t6 t5-1 > t6 ≥ t5 - c5 -1 such

that stimulus

stim1 was observed at t6

then at the next time point the sensitivity value of the

relation

stim2-a stays the same.

A lower-level model LM for the same adaptive

functionality is formalised below as a neurological

makeup NM together with the general neurological

activation rules NA. For the formalisation the

ontology from Table 2 were used.

LMP1 Neuron activation based on a stimulus

For any time point,

if a stimulus occurs,

then the neuron connected to this stimulus will be

activated for c5 following time points. Formally:

∀t5:TIME ∀st:STIMULUS ∀y:NEURON [

at(stimulusconnection(st, y) ∧ occurs(st), t5)

⇒ ∀t2:TIME t5 < t2 ≤ t5+c5 & at(activated(y), t2) ]

LMP2 Propagation of neuron activations

For any time point, if a neuron is activated, and this

neuron is connected to some other neuron by a synapse

with strength higher than B2,

then the other neuron will be also activated at the next

time point.

Table 2: State ontology for formalising the lower-level

model LM.

Sort Elements

NEURON sn1, sn2, mn

SYNAPSE S1, S2

VALUE natural numbers

Predicate Description

stimulusconnection: STIMULUS

x NEURON

Describes a connection

between a stimulus and a

(sensory) neuron

occurs: STIMULUS, occurs:

ACTION

Describes an occurrence

of a stimulus/action

activated: NEURON

Describes the activation

of a neuron

connectedvia: NEURON x

NEURON x SYNAPSE

Describes a connection

between two neurons by

a synapse

has_strength: SYNAPSE x

VALUE

Describes the strength of

a synapse

actionconnection: NEURON x

ACTION

Describes a connection

between a (preparatory)

neuron and an action

LMP3 Increase of the synapse’s strength

For any time point,

if two neurons connected by a synapse with strength

v are

activated

and at the previous time point both neurons were not

activated,

then at the next time point the strength of the synapse will

v+d(v). Formally:

∀t3:TIME ∀x,y:NEURON ∀s:SYNAPSE ∀v:VALUE [

at(activated(x) ∧ activated(y) ∧ connectedvia(x, y, s) ∧

has_strength(s, v), t3) & at(not(activated(x) ∧ activated(y)),

t3-1) ⇒ at(has_strength(s, v+d(v)), t3+1) ]

LMP4 Conditional persistency of the strength value of a

synapse

For any time point,

if the value of a synapse is v,

and not

both neurons are activated and

at the previous time point both neurons were not activated,

then the synapse’s strength remains the same.

LMP5 Occurrence of an action

For any time point,

if a neuron is not activated

and at the previous time point the neuron was activated,

then after c4 time points the action related to the neuron

will be performed.

The neurological makeup NM is assumed to be

stable in this example and is specified more formally

as follows (inspired by Aplysia’s makeup shown in

Fig. 1):

∀t:TIME at(stimulusconnection(stim1, SN1) ∧

stimulusconnection(stim2,SN2) ∧ connectedvia(SN,MN, S1)

∧ connectedvia(SN2, MN, S2) ∧ actionconnection(MN,

contraction) ∧ has_strength(S1,v1) ∧ has_strength(S2,v2),t)

ICAART 2009 - International Conference on Agents and Artificial Intelligence

Applying the Context-dependent Reduction

Approaches. An interpretation mapping from the

higher-level model HM to the lower-level model

LM can be defined as follows. The variables and

constants of sorts ACTION, STIMULUS, TIME,

VALUE are mapped without changes.

NA,NM

(v:DEGREE) = v:VALUE, where v is a

variable.

Suppose within the context of makeup NM,

stimulus

s is connected to the motoneuron MN via a

path passing synapse S, then:

NA,NM

(sensitivity(s, a, low)) = has_strength (S, v) ∧ v < B1

NA,NM

(sensitivity(s, a, medium)) = has_strength (S, v) ∧ B1

≤ v ∧ v ≤ B2

NA,NM

(sensitivity(s, a, high)) = has_strength (S, v) ∧ v > B2

NA,NM

(sensitivity(s, a, v)) = has_strength (S, v),

where v is a variable

To avoid clashes between names of variables,

every time when a new variable is introduced by a

mapping, it should be given a name different from

the names already used in the formula.

Note that the reduction relation depends on the

context NM. Within context NM sensitivity for

stimulus

stim1 relates to synapse S1 and sensitivity

for stimulus stim2 to synapse S2. Therefore, for

example,

NA,NM

(sensitivity(stim1, a, high)) = has_strength (S1, v) ∧

v > B2

NA,NM

(sensitivity(stim2, a, high)) = has_strength (S2, v) ∧

v > B2.

Here v is a variable of sort VALUE.

Observation and action predicates are mapped as

follows:

NA,NM

(observesstimulus(s)) = occurs(s)

NA,NM

(performsaction(a)) = occurs(a)

NA,NM

(has_successor(v, v')) = v’=v + d(v)

All other functional and predicate symbols of the

language of HM are mapped without changes.

Based on the mapping

NA,NM

as defined for basic

state properties, by compositionality the mapping of

more complex relationships is made as described in

Section 3.

This and other regularities derivable from the

higher-level specification HM can be mapped

automatically as described below in Section 5 onto

regularities that are derivable from NA ∪ NM, which

illustrates the criterion for interpretation mapping.

In similar manners the other two context-based

approaches can be applied to the case study. For

example, context-dependent bridge principles for NA

and context NM can be defined by (where the path

from stimulus

s to neuron MN is via synapse S):

sensitivity(s, a, low) ↔ has_strength (S, v) ∧ v < B1

sensitivity(s, a, medium) ↔ has_strength (S, v) ∧

B1 ≤ v ∧ v ≤ B2

sensitivity(s, a, high) ↔ has_strength (S, v) ∧ v > B2

observesstimulus(s) ↔ occurs(s)

performsaction(a) ↔ occurs(a)

has_successor(v, v') ↔ v’=v + d(v)

v:DEGREE ↔ v:VALUE

where v is a variable

Context-dependent functional reduction can be

applied by taking the joint causal role specification

for

sensitivity(stim2, a, low), sensitivity(stim2, a, medium),

sensitivity(stim2, a, high)

assuming that the sensitivity

of relation stim1-a is high.

5 IMPLEMENTATION

To perform an automated context-dependent

mapping of a higher level model specification to a

lower level model specification, a software tool has

been implemented in Java™ based on the mapping

principles described in Sections 3 and 4. As input for

this tool a higher level model specification in sorted

predicate logic is provided together with a set of

mappings of basic elements of the ontology used for

formalisation of the higher level specification. While

a mapping is being performed on any higher-level

formula, the tool traces possible clashes of variable

names and renames new variables when needed. As

a result, a specification in the lower level

specification language is generated.

The context-dependent interpretation mapping

should satisfy the reduction conditions described in

Section 3. For the case considered, these conditions

have the form: if a law (or property)

L is derived

from HM, then the corresponding mapping ϕ

NA,NM

(L)

should be derived from NA ∪ NM: HM |─ L

⇒ NA ∪

NM |─ ϕ

NA,NM

(L). This will be applied to the properties

in the specification

HM.

Since both HM and NA ∪ NM are specified using

the reified temporal predicate language, to establish

if a formula can be derived from a set of formulae,

the theorem prover Isabelle for many-sorted higher-

order logic has been used (Nipkow, Paulson and

Wenzel, 2002). As input for Isabelle a theory

specification is provided. A simple theory

specification consists of a declaration of ontologies,

lemmas and theorems to prove. Sorts are introduced

using the construct

datatype (e.g., datatype neuron =

sn1| sn2| mn

). Furthermore, sorts for higher-order

logics can be defined: e.g., sort STATPROP is defined

for the case study as:

datatype statprop= stimulusconnection event neuron|

activated neuron | occurs event | connectedvia neuron

neuron synapse | actionconnection neuron event |

has_strength synapse nat

RELATING KNOWLEDGE SPECIFICATIONS BY REDUCTION MAPPINGS

Here each element of

statprop refers to a state

property, expressed using the state ontology. The

elements of the state ontology should be also defined

in the theory : e.g.,

activated:: "neuron ⇒ statprop";

stimulusconnection:: "event ⇒ neuron ⇒ statprop"

. The

formulae of the state language are imported into the

reified language using the predicate

at:: "statprop ⇒

nat ⇒ bool".

The first theory specification defines the

following lemma expressing the criterion for the

mapping of the property HMP1 (Action

Performance), which expresses

NA ∪ NM |─ ∀t1:TIME [ at(has_strength (syn, v) ∧ v >

B2 ∧ occurs(s), t1)

⇒ ∃t2:TIME t2 > t1 & at(occurs(a), t2) ]

To enable the automated proof of this lemma the

implication introduction rule is applied (Nipkow,

Paulson and Wenzel, 2002), which moves the part

∀t1:TIME ∀s:STIMULUS [ at(has_strength (syn, v) ∧ v > B2

∧ occurs(s), t1)

to the assumptions. Then, the lemma

is proved automatically by the blast method, which

is an efficient classical reasoner. Note that for the

actual proof only the relevant part of

NA ∪ NM has

been used.

The second specification defines the lemma for

the mapping of the property HMP2 (Sensitivity

increase), which expresses

NA ∪ NM |─ ∀t1, t2:TIME ∀v, v’:VALUE [ t1+1 < t2 ≤

t1+c5+1 & at(occurs(stim1) ∧ has_strength (S1, var) ∧ var

> B2, t1) & at(occurs(stim2) ∧ has_strength (S2, v) ∧ v’=v

+ d(v), t2) ⇒ at(has_strength (S2, v’), t2+2) ]

For the proof of this lemma the same strategy has

been used as for the previous example. The proofs of

both examples have been performed in a fraction of

a second.

6 DISCUSSION

Within Cognitive Science, cognitive theories

provide higher-level descriptions of the functioning

of specific neural makeups. The concepts and

relationships used in the descriptions do not have a

direct one-to-one relationship to reality such as

concepts and relationships used within Physics or

Chemistry have. Due to the nontrivial dependence of

cognitive theories on the context of specific (neural)

makeups of individuals or species, relationships

between cognitive states are not considered genuine

universal laws; by changing the specific makeup

they simply can be refuted. Therefore they cannot

have a direct truth-preserving relationship to general

physical/biological laws. The classical approaches to

reduction do not take into account this context-

dependency in an explicit manner. Therefore, in this

paper refinements of these classical reduction

approaches are used that incorporate the context-

dependency in an explicit manner. These context-

dependent reduction approaches make explicit how

laws or regularities in a cognitive theory depend on

lower-level laws on the one hand and specific

makeups on the other hand. The detailed formalised

definitions of the approaches described in this paper

enable practical application to higher-level and

lower-level knowledge specification. As in the case

of cognitive theories, here the context-dependent

reduction approaches make explicit how concepts

and relationships in higher-level specifications relate

to lower-level specifications. Using these formalized

relations reduction approaches can be automated. In

particular, this paper illustrates how the

interpretation mapping approach can be automated,

including mapping of specifications and checking

the fulfilment of reduction criteria. In the example

considered the mapping of basic ontological

elements was assumed to be given. In the future

research approaches to identify basic ontological

mappings will be developed.

REFERENCES

Bennett, M. R., Hacker, P M.S., 2003. Philosophical

Foundations of Neuroscience. Malden, MA: Blackwell

Bickle, J., 1998. Psychoneural Reduction: The New Wave.

MIT Press.

Craver, C.F., 2001. Role Functions, Mechanisms and

Hierarchy. Philosophy of Science, vol. 68, pp. 31-55.

Galton, A., 2006. Operators vs Arguments: The Ins and

Outs of Reification. Synthese, vol. 150, pp. 415-441.

Gleitman, H., 2004. Psychology, W.W. Norton &

Company, New York.

Glennan, S. S., 1996. Mechanisms and the Nature of

Causation, Erkenntnis, vol. 44, pp. 49-71.

Hooker, C., 1981. Towards a General Theory of

Reduction. Dialogue, vol. 20, pp. 38-59, 201-236.

Kim, J., 1996. Philosophy of Mind. Westview Press.

Kim, J., 2005. Physicalism, or Something Near Enough.

Princeton University Press.

Kreisel, G., 1955. Models, translations and interpretations.

In Skolem, Th. Al. (eds.), Mathematical Interpretation

of Formal Systems. NH, Amsterdam, pp. 26-50.

Nagel, E., 1961. The Structure of Science. Harcourt, Brace

& World, New York.

Nipkow, T., Paulson, L. C., Wenzel, M., 2002.

Isabelle/HOL - A Proof Assistant for Higher-Order

Logic, vol. 2283 of LNCS. Springer-Verlag.

Schoenfield, J.R., 1967. Mathematical Logic. Addison-

Wesley.

Tarski, A., Mostowski, A., Robinson, R.M., 1953.

Undecidable Theories. North-Holland, Amsterdam.

ICAART 2009 - International Conference on Agents and Artificial Intelligence