STATE AGGREGATION FOR REINFORCEMENT LEARNING

USING NEUROEVOLUTION

Robert Wright and Nathaniel Gemelli

Air Force Research Lab, Information Directorate, 525 Brooks Rd., Rome, 13441, U.S.A.

Keywords:

Reinforcement learning, NeuroEvolution, Evolutionary algorithms, State aggregation.

Abstract:

In this paper, we present a new machine learning algorithm, RL-SANE, which uses a combination of neuroevo-

lution (NE) and traditional reinforcement learning (RL) techniques to improve learning performace. RL-SANE

is an innovative combination of the neuroevolutionary algorithm NEAT(Stanley, 2004) and the RL algorithm

Sarsa(λ)(Sutton and Barto, 1998). It uses the special ability of NEAT to generate and train customized neural

networks that provide a means for reducing the size of the state space through state aggregation. Reducing

the size of the state space through aggregation enables Sarsa(λ) to be applied to much more difﬁcult problems

than standard tabular based approaches. Previous similar work in this area, such as in Whiteson and Stone

(Whiteson and Stone, 2006) and Stanley and Miikkulainen (Stanley and Miikkulainen, 2001), have shown

positive and promising results. This paper gives a brief overview of neuroevolutionary methods, introduces

the RL-SANE algorithm, presents a comparative analysis of RL-SANE to other neuroevolutionary algorithms,

and concludes with a discussion of enhancements that need to be made to RL-SANE.

1 INTRODUCTION

Recent progress in the ﬁeld of neuroevolution has

lead to algorithms that create neural networks to solve

complex reinforcement learning problems (Stanley,

2004). Neuroevolution refers to technologies which

build and train neural networks through an evolution-

ary process such as a genetic algorithm. Neuroevolu-

tionary algorithms are attractive in that they are able

to automatically generate neural networks. Manual

engineering, domain expertise, and extensive training

data are no longer necessary to create effective neu-

ral networks. One problem with these algorithms is

that they rely heavily on the random chance of muta-

tion operators to produce networks of sufﬁcient com-

plexity and train them with the correct weights to

solve the problem at hand. As a consequence, neu-

roevolutionary methods can be slow or unable to con-

verge to a good solution. Traditional reinforcement

learning (RL) algorithms on the other hand take cal-

culated measures to improve their policies and have

been shown to converge very quickly. However, RL

algorithms rely on costly Q-tables or predetermined

function approximators to enable them to work on

complex problems. A hybrid of the two technologies

has the potential to provide an algorithm with the ad-

vantages of both.

We present a new machine learning algorithm,

which combines neuroevolution and traditional re-

inforcement learning techniques in a unique way.

RL-SANE

, Reinforcement Learning using State Ag-

gregation via Neuroevolution, is an algorithm de-

signed to take full advantage of neuroevolutionary

techniques to abstract the state space into a more

compact representation for a reinforcement learner

that is designed to exploit its knowledge of that

space. We have combined a neuroevolutionary algo-

rithm developed by Stanley and Miikkulainen called

NEAT(Stanley and Miikkulainen, 2001) with the re-

inforcement learning algorithm Sarsa(λ)(Sutton and

Barto, 1998). Neural networks serve as excellent

function approximators to abstract knowledge while

reinforcement learners are inherently good at ex-

ploring and exploiting knowledge. By utilizing the

It should be noted that RL-SANE is not related to the

SANE algorithm(Moriarty and Miikkulainen, 1997), Sym-

biotic Adaptive NeuroEvolution. SANE is a competing

neuroevolutionary algorithm with NEAT that uses a coop-

erative process to evolve NNs.

Wright R. and Gemelli N. (2009).

STATE AGGREGATION FOR REINFORCEMENT LEARNING USING NEUROEVOLUTION.

In Proceedings of the International Conference on Agents and Artiﬁcial Intelligence, pages 45-52

DOI: 10.5220/0001658800450052

 SciTePress

strengths of both of these methods we have created

a robust and efﬁcient machine learning approach in

RL-SANE.

The rest of the paper is organized as follows. Sec-

tion 2 will give an overview of the problem on which

are working and other state aggregation approaches

that have been done. Section 3 will provide a full de-

scription and discussion on the RL-SANE algorithm.

In sections 4.3 and 4.4 we will provide experimen-

tal results for RL-SANE. Section 4.3 provides in-

sight into how the β parameter affects performance

and how it can be determined. Section 4.4 completes

the analysis with a comparison of RL-SANE’s perfor-

mance versus a standard neuroevolutionary approach,

NEAT, on two standard benchmark problems. Finally,

section 5 will highlight our future work.

2 BACKGROUND

The state aggregation problem for machine learning

has started to gain more momentum over the past

decade. Singh et al. used soft state aggregation meth-

ods in (Singh et al., 1995) and discussed how impor-

tant compact representations are to learning methods.

Stanley and Miikkulainen (Stanley and Miikkulainen,

2002) discuss using neural networks for state aggre-

gation and learning and demonstrated promising re-

sults for real-world applications. Further improve-

ments to neuroevolutionary approaches were done in

Siebel et al. in (Siebel et al., 2007) and combina-

tions of neuroevolution and reinforcement learning

were studied in Whiteson and Stone in (Whiteson

and Stone, 2006). Neuroevolution has been shown

to be one of the strongest methods for solving com-

mon benchmarking problems, such as pole-balancing

(Stanley and Miikkulainen, 2002). This section will

highlight neuroevolution and describe the NEAT al-

gorithm which we use as a benchmark to compare our

work against.

2.1 Neuroevolution

Neuroevolution (NE) (Stanley and Miikkulainen,

2001) is a technology that encompasses techniques

for the artiﬁcial evolution of neural networks. Tra-

ditional work in neural networks used static neural

networks that were designed by subject matter ex-

perts and engineers. This method showed the power

of neural networks in being able to model and learn

non-linear functions. However, the static nature of

these structures limited their scope and applicability.

More recent advances in the ﬁeld of neuroevolution

have shown that it is possible to build and conﬁgure

these networks dynamically through the use of special

mutation operators in a genetic algorithm (GA) (Stan-

ley, 2004). These advances have made it possible

to automatically generate and train special purpose

neural networks for solving difﬁcult multi-parameter

problems. We recognize similar work in this area as

in Siebel et al. (Siebel et al., 2007), Stanley et al.

(Stanley and Miikkulainen, 2001), and Whiteston and

Stone (Whiteson and Stone, 2006) exists and below

we describe one such algorithm, NEAT.

2.2 NEAT

NeuroEvolution of Augmenting Topologies (NEAT)

is a neuroevolutionary algorithm and framework

which uses a genetic algorithm to evolve populations

of neural networks. It is a neuroevolutionary algo-

rithm that evolves both the network topology and

weights of the connections between the nodes in the

network(Stanley and Miikkulainen, 2002). The au-

thors, Stanley et al., found that by evolving both the

network topology and the connection weights, they

solved typical RL benchmark problems several times

faster than competing RL algorithms(Stanley and Mi-

ikkulainen, 2001) with signiﬁcantly less system re-

sources. The algorithm starts with a population of

simple perceptron networks and gradually, through

the use of a genetic algorithm (GA), builds more com-

plex networks with the proper structure to solve a

problem. It is a bottom-up approach which takes

advantage of incremental improvements to solve the

problem. The results are networks that are automat-

ically generated, not overly complicated in terms of

structure, and custom tuned for the problem at hand.

Two of the most powerful aspects of NEAT

which allow for such good benchmark perfor-

mance and proper network structure are complexiﬁ-

cation(Stanley, 2004) and speciation(Stanley and Mi-

ikkulainen, 2002). Complexiﬁcation, in this context,

is an evolutionary process of constructing neural net-

works through genetic mutation operators. These ge-

netic mutation operators are: modify weight, add link,

and add node (Stanley, 2004). Speciation is a method

for protecting newly evolved neural network struc-

tures (specie) into the general population, and prevent

them from having to compete with more optimized

species (Stanley, 2004). This is important to preserve

new (possibly helpful) structures with less optimized

network weights.

ICAART 2009 - International Conference on Agents and Artificial Intelligence

3 RL-SANE

RL-SANE is the algorithm we have developed which

is a combination of NEAT and a RL algorithm

(Sarsa(λ)(Sutton and Barto, 1998)). This combina-

tion was chosen because neural networks have been

shown to be effective at reducing the complexities of

state spaces for RL algorithms(Tesauro, 1995). NEAT

was chosen as a way for providing the neural net-

works because it is able to build and train networks

automatically and effectively. Sarsa(λ) was chosen

because of its performance characteristics. Any NE

algorithm that automatically builds neural networks

can be substituted for NEAT and any RL algorithm

can be substituted in Sarsa(λ)’s place, and RL-SANE

should still function.

RL-SANE uses NE to evolve neural networks

which are bred speciﬁcally to interpret and aggregate

state information. NEAT networks take the raw per-

ception values and ﬁlter the information for the RL

algorithm by aggregating inputs together which are

similar with respect to solving the problem

. This re-

duces the state space representation and enables tradi-

tional RL algorithms, such as Sarsa(λ), to function on

problems where the raw state space of the problem is

too large to explore. NEAT is able to create networks

which accomplish the ﬁltering by evolving networks

that improve the performance of Sarsa(λ) in solving

the problem. Algorithm 1 provides the pseudo code

for RL-SANE and describes the algorithm in greater

detail.

What differentiates RL-SANE from other algo-

rithms which use NE to do learning, such as in NEAT,

is that RL-SANE separates the two mechanisms that

perform the state aggregation and policy iteration.

Previous NE algorithms(Stanley and Miikkulainen,

2001)(Whiteson and Stone, 2006) use neural net-

works to learn a function which not only encompasses

a solution to the state aggregation problem, but the

policy iteration problem as well. We believe this over-

burdens the networks and increases the likelihood of

“interference”(Carreras et al., 2002). In this context,

“interference” is the problem of damaging one aspect

of the solution while attempting to ﬁx another. RL-

SANE, instead, only uses the neural networks to per-

form the state aggregation and uses Sarsa(λ) to per-

form the policy iteration which reduces the potential

impact of interference.

The purpose of the neural networks created by

the NEAT component is to ﬁlter the state space for

“With respect to the problem” in this paper refers to

groupings made by NEAT which improve Sarsa(λ)’s ability

to solve the problem, not necessarily the grouping of similar

perceptual values.

Algorithm 1 RL-SANE(S,A,p,m

,g,e,α,β,γ,λ,ε)

1: //S: set of all states, A: set of all actions

2: //p: population size, m

: set of all states, m

: link mutation rate

3: //m

: link removal mutation rate, g: number of generations

4: //e: number of episodes per generation, α: learning rate

5: //β: state bound, γ: discount factor, λ: eligibility decay rate

6: //ε: ε-Greedy probability

7: P[] ← INIT-POPULATION(S,p) // create a new population P of random

networks

8: Q

[] ← new array size p // initialize array of Q tables

9: for i ← 1 to g do

10: for j ← 1 to p do

11: N,Q[] ← P[ j], Q

[ j] // select network and Q table

12: if Q[] = null then

13: Q[]←new array size β // create a new Q table

14: end if

15: for k ← 1 to e do

16: s,s

←null, INIT-STATE(S) // initialize the state

17: repeat

18: s

←INT-VAL(EVAL-NET(N,s

)*β) // determine the

state id

19: with-prob(ε) a

←RANDOM(A) // ε-Greedy action se-

lection

20: else a

←argmax

Q[s

,l]

21: if s6=null then

22: SARSA(r,a,a

,λ,γ,α,Q[],s

)//update Q table

23: end if

24: s

,s,a←s

25: r,s

←TAKE-ACTION(a

)

26: N. f itness←N. f itness+r // update the ﬁtness of the net-

work

27: until TERMINAL-STATE(s)

28: end for

29: Q

[ j]←Q[] // update array of Q tables

30: end for

31: P

[],Q

← new arrays size p // array for next generation

32: for j←1 to p do

33: P

[ j],Q

[ j]←BREED-NET(P[],Q

[]) // make a new network and

Q table based on parents

34: with-probability m

: ADD-NODE-MUTATION(P

[ j])

35: with-probability m

: ADD-LINK-MUTATION(P

[ j])

36: with-probability m

: REMOVE-LINK-MUTATION(P

[ j])

37: end for

38: P[],Q

[]←P

[],Q

[]

39: end for

Sarsa(λ). They do this by determining if different

combinations of perceptual inputs should be consid-

ered unique states with respect to the problem. This is

done by mapping the raw multi-dimensional percep-

tual information onto a single dimensional continuum

which is a real number line in the range [0..1]. The

state bound parameter, β, divides the continuum into

a speciﬁed number of discrete areas and provides an

upper bound on the number of possible states there are

in the problem. All points on the continuum within

a single area are considered to be the same state by

RL-SANE and are labeled with a unique state iden-

tiﬁer. The output of the neural networks, given a set

STATE AGGREGATION FOR REINFORCEMENT LEARNING USING NEUROEVOLUTION

of perception values, is the state identiﬁer of the area

the perception values map on to the continuum. RL-

SANE uses this state identiﬁer as input to the Sarsa(λ)

RL component as an index into its Q-table. The Q-

table is used to keep track of values associated with

taking different actions in speciﬁc states. The net-

works which are best at grouping perception values

that are similar with respect to solving the problem

will enable Sarsa(λ) to learn how to solve the prob-

lem more effectively.

Sarsa(λ) provides a ﬁtness metric for each net-

work to NEAT by reporting the aggregate reward it

received in attempting to learn the problem. This

symbiotic relationship provides NEAT with a ﬁtness

landscape for discovering better networks. This also

provides Sarsa(λ) with a mechanism for coping with

complex state spaces, via reducing complexity. Re-

ducing the complexity of the state space makes the

problem easier to solve by reducing the amount of ex-

ploration needed to calculate a good policy. It also

needs to be stated that Q-tables persist with the neural

networks they are trained on throug out the evolution

of the networks. When crossover occurs in NEAT’S

GA, the Q-table of the primary parent gets passed on

to the child neural network.

Selection of an appropriate or optimal state bound

(β) is of great importance to the performance of the al-

gorithm. If the selected state bound is too small, sets

of perception values that are not alike with respect to

the problem will be aggregated into the same state.

This may hide relevant information from Sarsa(λ) and

prevent it from ﬁnding the optimal, or even a good,

policy. If the state bound is too large, then percep-

tion sets that should be grouped together may map

to different states. This forces Sarsa(λ) to experi-

ence and learn more states than are necessary. Ef-

fectively, this slows the rate at which Sarsa(λ) is able

to learn a good policy because it is experiencing and

exploring actions for redundant states, causing bloat.

Bloat makes the Q-tables larger than necessary, in-

creasing the memory footprint of the algorithm. Im-

proper state bound values have adverse effects on the

performance of RL-SANE. Section 4.3 provides some

insight into how varying β values affects RL-SANE’s

performance and gives guidance on how to set β.

We recognize that RL-SANE is not the ﬁrst al-

gorithm that attempts to pair NE techniques with

a traditional RL algorithm. NEAT+Q by Whiteson

and Stone (Whiteson and Stone, 2006) combines Q-

learning (Watkins and Dayan, 1992) with NEAT in a

different way than RL-SANE. In NEAT+Q the neural

networks are meant to output literal Q-values for all

the actions available in the given state. The networks

are trained on-line to produce the correct Q-values via

the Q-learning update function and the use of back-

propagation (Rumelhart et al., 1988). We attempted

to use NEAT+Q in our analysis of RL-SANE but we

were unable to duplicate the results found in (White-

son and Stone, 2006), so we are unable to present a

comparison. Also, both RL-SANE and NEAT+Q are

not easily adapted to work on problems with continu-

ous action spaces, whereas NEAT is. RL-SANE and

NEAT+Q both make discrete choices of actions.

4 EXPERIMENTS

This section describes our experimental setup for an-

alyzing the performance of the RL-SANE algorithm.

In our experiments we compare RL-SANE’s per-

formance on two well known benchmark problems,

mountain car (Boyan and Moore, 1995) and double

inverted pendulum (Gomez and Miikkulainen, 1999),

against itself with varying β values and against that of

NEAT. NEAT was chosen as the benchmark algorithm

of comparison because it is a standard for neuroevo-

lutionary algorithms (Whiteson and Stone, 2006).

Both of the algorithms for our experiments were

implemented using Another NEAT Java Implemen-

tation (ANJI)(James and Tucker, 2004). ANJI is a

NEAT experimentation platform based on Kenneth

Stanley’s original work written in Java. ANJI includes

a special mutation operator not included in the orig-

inal NEAT algorithm that randomly prunes connec-

tions in the neural networks. This mutation operator is

beneﬁcial in that it attempts to remove redundant and

excess structure from the neural networks. The prune

operator was enabled and used by each algorithm in

our experiments. For our experiments we used the

default parameters for ANJI with the exceptions that

we disallowed recurrent networks and we limited the

range of the weight values to be [-1..1]. We disal-

lowed recurrency to reduce their overall complexity

of the networks and we bounded the link weights so

the calculation of the state from the output signal is

trivial.

4.1 Mountain Car

The mountain car problem (Boyan and Moore, 1995)

is a well known benchmark problem for reinforce-

ment learning algorithms. In this problem a car begins

somewhere in the basin of a valley, of which it must

escape. See Figure 1 for an illustration of the prob-

lem. Unfortunately, the car’s engine is not powerful

enough to drive directly up the hill from a standing

start at the bottom. To get out of the valley and reach

the goal position the car must build up momentum

ICAART 2009 - International Conference on Agents and Artificial Intelligence

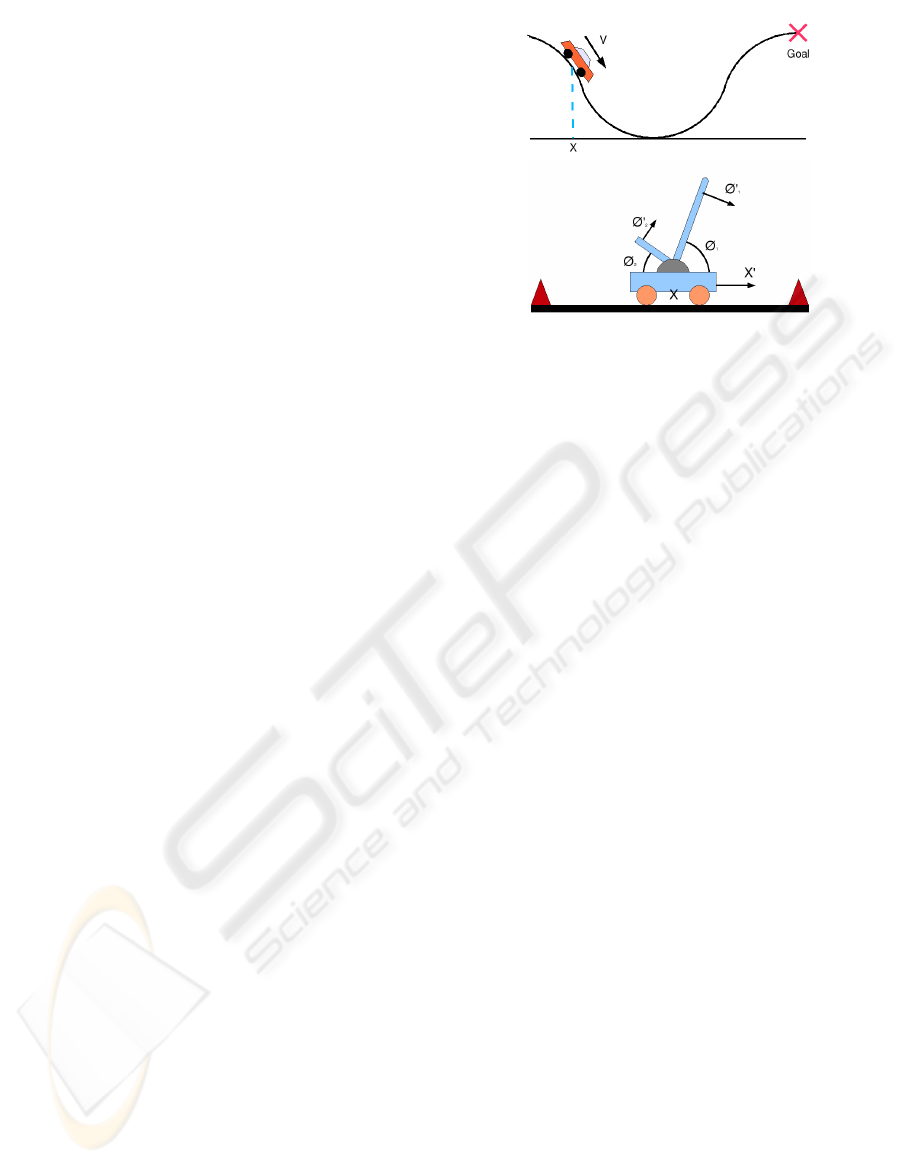
from gravity by driving back and forth, up and down

each side of the valley.

For this problem the learner has two perceptions:

the position of the car, X, and the velocity of car, V .

Time is discretized into time steps and the learner is

allowed one of two actions, drive forward or back-

ward, during each time step. The only reward the

learner is given is a value of -1 for each time step

of the simulation in which it has not reached the

goal. Because the RL algorithms are seeking to max-

imize aggregate rewards, this negative reward gives

the learner an incentive to learn a policy which will

reach the goal in as few time steps as possible.

The mountain car problem is a challenging prob-

lem for RL algorithms because it has continuous in-

puts. The problem has an almost inﬁnite number of

states if each set of distinct set perceptual values is

taken to be a unique state. It is up to the learner or the

designer of the learning algorithm to determine under

what conditions the driver of the car should consider

a different course of action.

In these experiments the populations of neural net-

works for all of the algorithms have two input nodes,

one for X and one for V , which are given the raw

perceptions. NEAT networks have three output nodes

(one for each direction the car can drive plus coasting)

to specify the action the car should take. RL-SANE

networks have a single output node which is used to

identify the state of the problem.

Individual episodes are limited to 2500 time steps

to ensure evaluations will end. Each algorithm was

recored for 25 different runs using a unique random

seed for the GA. The same set of 25 random seeds

were used in evaluating all three algorithms. Runs

were composed of 100 generations in which each

member of the population was evaluated over 100

episodes per generation. The population size for the

GA was set to 100 for every algorithm. Each episode

challenged the learner with a unique instance of the

problem from a ﬁxed set that starts with the car in a

different location or having a different velocity. By

varying the instances over the episodes we helped en-

sure the learners were solving the problem and not

just a speciﬁc instance.

4.2 Double Inverted Pendulum

Balancing

The double inverted pendulum balancing problem

(Gomez and Miikkulainen, 1999) is a very difﬁcult

RL benchmark problem. See ﬁgure 1 for an illustra-

tion of this problem. In this problem the learner is

tasked with learning to balance two beams of differ-

ent mass and length attached to a cart that the learner

Figure 1: These ﬁgures illustrate the two RL benchmark

problems, (Above)mountain car and (Below) double in-

verted pendulum balancing.

can move. The learner has to prevent the beams from

falling over without moving the cart past the barriers

which restrict the cart’s movement. If the learner is

able to prevent the beams from falling over for a spec-

iﬁed number of time steps the problem is considered

solved.

The learner is given six perceptions as input: X is

the position of the cart, X

is the velocity of the cart, θ

1 and 2 are the angles of the beam, and θ

1 and 2 are

the angular velocities of the beams. At any given time

step the learner can do one of the following actions:

push the cart left, push the cart right, or not push the

cart at all.

Like the mountain car problem, this problem is

very difﬁcult for RL algorithms because the percep-

tion inputs are continuous. This problem is much

more difﬁcult in that it has three times as many per-

ceptions giving it a dramatically larger state space. In

these experiments each algorithm trains neural net-

works that have six input nodes, one for each per-

ception. NEAT has three output nodes, one for each

action. RL-SANE only has one output node for the

identiﬁcation of the current state.

In this set of experiments the algorithms were

tasked with creating solutions that could balance the

pendulum for 100000 time steps. Each algorithm

was evaluated over 25 different runs where the ran-

dom seed was modiﬁed. Again, the same set of ran-

dom seeds was used in evaluating all three algorithms.

Runs were composed of 200 generations with a popu-

lation size of 100. In each generation, every member

of the population was evaluated on 100 different in-

stances of the inverted pendulum problem. The aver-

age number of steps the potential solution was able to

balance the pendulum over the set of 100 determined

its ﬁtness.

STATE AGGREGATION FOR REINFORCEMENT LEARNING USING NEUROEVOLUTION

4.3 Changing the Size of State Bounds

Figure 3 shows convergence graphs for RL-SANE us-

ing varying β values, the state bound, on both bench-

mark problems. The graphs show the average number

of steps the most ﬁt members of the population were

able to either solve the mountain car problem in or

balance the beams for. For the mountain car experi-

ments fewer steps taken is better and for the double

inverted pendulum problem the more steps the beams

were balanced for the better. For these experiments

we varied the β parameter from equal to the number of

actions available in the problems (3) up to 1000. The

purpose of these experiments is to show how varying

the β parameter affects the performance of the RL-

SANE algorithm.

When β is set equal to the number of actions avail-

able the neural networks do all the work. They have

to identify the state and determine the policy. All the

Sarsa(λ) component is doing is choosing which ac-

tion best corresponds with the output of the network.

What is interesting is if you compare the correspond-

ing graphs from ﬁgure 3 and ﬁgure 4 when β equals 3

the performance of RL-SANE is still better than that

of NEAT. This is interesting because the networks

from both algorithms are both performing the same

function and are effectively produced by the same al-

gorithm, NEAT. The reason RL-SANE has an advan-

tage over standard NEAT in this case is that Sarsa(λ)

helps RL-SANE choose the best action corresponding

with the network output whereas the actions in NEAT

are ﬁxed to speciﬁc outputs. This result shows that

RL-SANE’s performance on problems with discrete

actions spaces is going to be as good or better than

that of NEAT if β is set to a small value. Smaller

β values preferred because they limit the size of the

Q-tables RL-SANE requires and it improves the solu-

tion’s generality.

As β is increased from 3 to larger values we see

the performance of RL-SANE improve, but once the

value of β exceeds a certain value the performance of

RL-SANE begins to drop. The performance increase

can be attributed to a burden shift from the NN to the

RL component. Sarsa(λ) is much more efﬁcient at

performing the policy iteration than the NEAT com-

ponent. Eventually the performance degrades because

the NN(s) begin to identify redundant states as being

different, which increases the amount of experience

necessary for the RL component to learn. This behav-

ior is what we expected and shows that there might

convex ﬁtness landscape for β values. A convex ﬁt-

ness landscape would mean that proper β values could

be found by a simple hill climbing algorithm instead

of having to specify them a priori.

Figure 2: This ﬁgure shows the structure of typical solution

neural networks for the mountain car problem. The β value

for RL-SANE was set to 50.

It is also interesting that the double inverted pen-

dulum problem runs are more sensitive to the value of

β than the mountain car problem runs are. We are not

certain of the reason for this behavior. This requires

further investigation, and we hypothesize that more

complex problems will be more sensitive to β value

selection.

4.4 NEAT Comparison

Figure 4 show convergence graphs comparing the RL-

SANE to NEAT on the benchmarks. The error bars

on the graphs indicate 95% conﬁdence intervals over

the entire set of experiments to show statistical signif-

icance of the results. As can be seen from the charts

the RL-SANE algorithm is able to converge to the ﬁ-

nal solution in far fewer generations and with a greater

likelihood of success than NEAT in both sets of exper-

iments. NEAT is only able to solve the entire double

inverted pendulum problem set in just 2 of the 25 runs

of experiments. The performance difference between

RL-SANE and NEAT increases dramatically from the

mountain car to double inverted pendulum problem

which implies that RL-SANE may scale to more dif-

ﬁcult problems better than NEAT.

Figures 2 and 5 show the structure of typical so-

lution NN(s) for both RL-SANE and NEAT on both

problems. In both ﬁgures the RL-SANE networks are

much less complex than the NEAT networks. These

results are not very surprising in that the RL-SANE

networks are performing a less complicated function,

state aggregation. NEAT networks need to perform

their own version of state abstraction and policy itera-

tion. The fact the RL-SANE networks do not need to

be as complicated as NEAT networks explains why

RL-SANE is able to perform better than NEAT on

these benchmarks. If the NN’s do not need to be as

complex they have a greater likelihood of being pro-

duced by the GA earlier in the evolution. This result

also supports our belief that RL-SANE will scale bet-

ter to more complex problems than standard NEAT.

ICAART 2009 - International Conference on Agents and Artificial Intelligence

100

200

300

400

500

600

700

0 5 10 15 20

Steps

Generations

Beta 3

Beta 5

Beta 10

Beta 50

Beta 100

Beta 1000

20000

40000

60000

80000

100000

120000

0 50 100 150 200

Steps

Generations

Beta 3

Beta 5

Beta 10

Beta 50

Beta 100

Beta 1000

Figure 3: Shows the performance of the RL-SANE algo-

rithm using varying β values on the mountain car (Above)

and the double inverted pendulum (Below) problems.

5 FUTURE WORK

5.1 State Bounding

RL-SANE, in its current form, depends on the state

bound parameter, β, for the problem to be known a

priori. For an algorithm that is intended to reduce or

eliminate the need for manual engineering or domain

expertise. In many cases, this a prior knowledge is

not available. Much of our future research effort will

be placed on developing a method for automatically

deriving the state bound value. For reasons stated

in section 3 and 4.3 we believe that the problem of

ﬁnding good β values has a convex landscape that a

hill climbing algorithm, such as a GA, can properly

search. In our future research we will explore dif-

ferent methods for calculating β automatically, even

perhaps during the evolution of solving the problem.

5.2 RL-SANE Scaling

Our background research on RL and methods for han-

dling large state spaces revealed a lack of work done

100

150

200

250

300

350

0 10 20 30 40 50

Steps

Generations

RL-SANE

NEAT

20000

40000

60000

80000

100000

120000

0 50 100 150 200

Steps

Generations

RL-SANE

NEAT

Figure 4: Shows the performance of the RL-SANE al-

gorithm compared to that of NEAT on the mountain car

(Above) and the double inverted pendulum (Below) prob-

lems. The RL-SANE runs used a β value of 50 for the

mountain car problem and 10 for the double inverted pen-

dulum problem.

Figure 5: This ﬁgure shows the structure of typical solution

neural networks for the double inverted pendulum problem.

The β value for RL-SANE was set to 10.

to examine just how well these methods scale towards

ever more complicated problems. This is surpris-

ing considering that there are so many algorithms de-

signed to improve the scaling of RL algorithms to-

wards larger state spaces. In the works that we have

examined, the authors generally chose a single in-

stance of a problem that was difﬁcult or impossible

for existing algorithms. They then showed how their

algorithms could solve that instance. In our future

work we intend to perform experiments that stress and

STATE AGGREGATION FOR REINFORCEMENT LEARNING USING NEUROEVOLUTION

examine the scalability of RL-SANE and the other

neuroevolutionary based algorithms, such as NEAT,

NEAT+Q, and EANT (Siebel et al., 2007), to ﬁnd out

just how far these algorithms can be pushed.

6 CONCLUSIONS

In this paper, we have introduced the RL-SANE al-

gorithm, explored its performance under varying β

values, and provided a comparative analysis to other

neuroevolutionary learning approaches. Our exper-

imental results have show that RL-SANE is able to

converge to good solutions over less iterations and

with less computational expense than NEAT even

with naively speciﬁed β values. The combination of

neuroevolutionary methods to do state aggregation for

traditional reinforcement learning algorithms appears

to have real merit. RL-SANE is, however, dependent

on the β parameter which must be calculated a priori.

We have shown the importance of the derivation of

proper β parameters and suggested ﬁnding methods

for automating the derivation of β as a direction for

future research.

Building off of what has been done by previ-

ous neuroevolutionary methods, we have found that

proper decomposition of the problem into state aggre-

gation and policy iteration is relevant. By providing

this decomposition, RL-SANE should be more appli-

cable to higher complexity problems than existing ap-

proaches.

REFERENCES

Boyan, J. A. and Moore, A. W. (1995). Generalization in re-

inforcement learning: Safely approximating the value

function. In Tesauro, G., Touretzky, D. S., and Leen,

T. K., editors, Advances in Neural Information Pro-

cessing Systems 7, pages 369–376, Cambridge, MA.

The MIT Press.

Carreras, M., Ridao, P., Batlle, J., Nicosebici, T., and Ur-

sulovici, Z. (2002). Learning reactive robot behav-

iors with neural-q learning. In IEEE-TTTC Interna-

tional Conference on Automation, Quality and Test-

ing, Robotics. IEEE.

Gomez, F. J. and Miikkulainen, R. (1999). Solving non-

markovian control tasks with neuro-evolution. In IJ-

CAI ’99: Proceedings of the Sixteenth International

Joint Conference on Artiﬁcial Intelligence, pages

1356–1361, San Francisco, CA, USA. Morgan Kauf-

mann Publishers Inc.

James, D. and Tucker, P. (2004). A comparative analysis

of simpliﬁcation and complexiﬁcation in the evolution

of neural network topologies. In Proceedings of the

2004 Conference on Genetic and Evolutionary Com-

putation. GECCO-2004.

Moriarty, D. E. and Miikkulainen, R. (1997). Forming neu-

ral networks through efﬁcient and adaptive coevolu-

tion. Evolutionary Computation, 5:373–399.

Rumelhart, D. E., Hinton, G. E., and Williams, R. J.

(1988). Learning representations by back-propagating

errors. Neurocomputing: foundations of research,

pages 696–699.

Siebel, N. T., Krause, J., and Sommer, G. (2007). Efﬁcient

Learning of Neural Networks with Evolutionary Algo-

rithms, volume Volume 4713/2007. Springer Berlin /

Heidelberg, Heidelberg, Germany.

Singh, S. P., Jaakkola, T., and Jordan, M. I. (1995). Re-

inforcement learning with soft state aggregation. In

Tesauro, G., Touretzky, D., and Leen, T., editors,

Advances in Neural Information Processing Systems,

volume 7, pages 361–368. The MIT Press.

Stanley, K. O. (2004). Efﬁcient evolution of neural networks

through complexiﬁcation. PhD thesis, The University

of Texas at Austin. Supervisor-Risto P. Miikkulainen.

Stanley, K. O. and Miikkulainen, R. (2001). Evolving neu-

ral networks through augmenting topologies. Techni-

cal report, University of Texas at Austin, Austin, TX,

USA.

Stanley, K. O. and Miikkulainen, R. (2002). Efﬁcient

reinforcement learning through evolving neural net-

work topologies. In GECCO ’02: Proceedings of the

Genetic and Evolutionary Computation Conference,

pages 569–577, San Francisco, CA, USA. Morgan

Kaufmann Publishers Inc.

Sutton, R. S. and Barto, A. G. (1998). Reinforcement Learn-

ing: An Introduction (Adaptive Computation and Ma-

chine Learning). The MIT Press.

Tesauro, G. (1995). Temporal difference learning and td-

gammon. Commun. ACM, 38(3):58–68.

Watkins, C. J. C. H. and Dayan, P. (1992). Q-learning. Ma-

chine Learning, 8(3-4):279–292.

Whiteson, S. and Stone, P. (2006). Evolutionary function

approximation for reinforcement learning. Journal of

Machine Learning Research, 7:877–917.

ICAART 2009 - International Conference on Agents and Artificial Intelligence