APPROXIMATED WINNER DETERMINATION FOR A SERIES OF

COMBINATORIAL AUCTIONS

Naoki Fukuta

Faculty of Informatics, Shizuoka University, 3 5 1, Johoku Hamamatsu Shizuoka, Japan

Takayuki Ito

Graduate School of Engineering, Nagoya Institute of Technology, Gokisocho, Showa-ku, Nagoya, Japan

Sloan School of Management, Massachusetts Institute of Technology, 5 Cambridge Center

Cambridge Massachusetts, MA, U.S.A.

Keywords:

Combinatorial auctions, Winner determination, Approximation algorithm.

Abstract:

In this paper, we propose approximated winner determination algorithms for iteratively conducted combina-

torial auctions. Our algorithms are designed to effectively reuse last-cycle solutions to speed up the initial

approximation performance on the next cycle. Experimental results show that our proposed algorithms out-

perform existing algorithms when a large number of similar bids are contained through iterations. Also, we

propose an enhanced algorithm that effectively avoids the undesirable reuse of the last solutions in the algo-

rithm without serious computational overheads.

1 INTRODUCTION

Combinatorial auctions(Cramton et al., 2006), one

of the most popular market mechanisms, have a

huge effect on electronic markets and political strate-

gies. For example, Sandholm et al. (Sandholm

et al., 2005)(Sandholm, 2007) proposed real mar-

kets using their innovative combinatorial auction al-

gorithms. The FCC tried to employ combinatorial

auction mechanisms to assign spectrums to compa-

nies (McMillan, 1994). Also (Cramton et al., 2006)

shows other realistic examples that utilize combinato-

rial auction mechanisms.

We argue that demand exists to utilize combina-

torial auction mechanisms that cannot be covered by

existing approaches due to hard time constraints and

the limitations of usable computationalresources. Re-

source allocation for agents in ubiquitous computing

environmentsis a good example for understanding the

needs of the short-time approximation of combinato-

rial auctions. In such an environment, agents must

provide speciﬁc services to their users using various

available resources. However, in ubiquitous comput-

ing environments, since such resources as sensors and

devices are typically limited, they do not satisfy all

the needs of all agents. For various reasons including

physical limitations and privacy concerns, most of the

resources cannot be shared with other agents. Fur-

thermore, agents will simultaneously use two or more

resources to realize desirable services for users. Since

agents provide services to their own users, agents

might be self-interested. Therefore, a combinatorial

auction mechanism is a good option for such situa-

tions since it provides effective resource allocation to

self-interested agents.

In order to utilize combinatorial auctions on the

above situation, we need to complete winner deter-

mination within a very short time. Consider 256 re-

sources and 100 agents, where each agent places, for

example, from 200 to 1,000 of combinations for the

items as complex bids to an auction, they will be ex-

panded to, from 20,000to 100,000 of atomic OR-bids.

Here, to avoid occupying a set of resources for a long

time by a certain agent, we consider a resource allo-

cation scenario based on ﬁxed time slice assignment

model. In the scenario, those resources are auctioned

and allocated from a system to agents for a ﬁxed time

period. After a certain time has passed, those are once

all returned to the system and then they are auctioned

again for the next period. When an agent prefers to

continue using the same resources at the next period,

the agent will place a higher price for the resources to

increase the possibility to win them.

In ubiquitous computing scenarios, since physi-

cal locations of users are always changing, resources

should be reallocated in a certain period to catch up

400

Fukuta N. and Ito T. (2009).

APPROXIMATED WINNER DETERMINATION FOR A SERIES OF COMBINATORIAL AUCTIONS.

In Proceedings of the International Conference on Agents and Artiﬁcial Intelligence, pages 400-407

DOI: 10.5220/0001659104000407

 SciTePress

with those changes. For better usability, the resource

reallocation time period will be 0.1 to several seconds

depending on services provided. Furthermore, since

we should complete whole resource allocation proce-

dure that includes pricing and communication to de-

vices for actual resource assignment, we must deter-

mine auction winners within an extremely short time

period that is far less than the actual resource alloca-

tion period.

In general, the optimal winner determina-

tion problem of combinatorial auctions is NP-

hard(Cramton et al., 2006). Thus, much work fo-

cuses on tackling the computational costs for win-

ner determination (Fujishima et al., 1999)(Cramton

et al., 2006)(Sandholm et al., 2005). Some works

(Lehmann et al., 2002) (Zurel and Nisan, 2001) (Hoos

and Boutilier, 2000) try to achieve approximate solu-

tions in winner determination.

In this paper, we propose enhanced approxima-

tion algorithms of winner determination on combina-

torial auctions that are suitable for the purpose of iter-

ative reallocation of items mentioned above. Since the

above-mentioned existing algorithms are ofﬂine algo-

rithms, we need to re-calculate the winners when bids

are added to or deleted from the auction even when

the modiﬁcation of bids is only slight. Intuitively, it

could be helpful to reuse results of past similar auc-

tions for faster approximation of the current auction.

However, those algorithms did not consider reusing

past approximated results for performance improve-

ment since such reuse may cause serious performance

down in certain cases. Our enhanced algorithms pre-

pared mechanisms to reuse past approximationresults

but avoid such performance down with very small

overhead.

2 PRELIMINARIES

2.1 Winner Determination Problem

In this paper, to keep simplicity of discussion, we

only focus on utility-based resource allocation prob-

lems(Thomadakis and Liu, 1999), rather than generic

resource allocation problems with numerous complex

constraints. Utility-based resource allocation prob-

lem is a problem that aims to maximize the sum of

utilities of users for each allocation period, but does

not consider other factors and constraints (i.e., fair al-

location (Andrew et al., 2008) , security and privacy

concerns(Xie and Qin, 2008), uncertainty(Xiao et al.,

2004), etc). Also we only consider a scenario that is

based on ﬁxed time slice assignment model.

Combinatorial auction is an auction mechanism

that allows bidders to locate bids for a bundle of

items rather than single item(Cramton et al., 2006).

When we apply combinatorial auction mechanism for

utility-based resource allocation problems, the prob-

lem can be transformed to solve a winner determina-

tion problem on combinatorial auctions.

The winner determination problem on combina-

torial auctions is deﬁned as follows(Cramton et al.,

2006) : The set of bidders is denoted by N = 1,...,n,

and the set of items by M = {1,...,m}. |M| = m.

Bundle S is a set of items : S ⊆ M. We denote by v

(S),

bidder i’s valuation of combinatorial bid for bundle S.

An allocation of the items is described by variables

(S) ∈ {0,1}, where x

(S) = 1 if and only if bidder i

wins the bundle S. An allocation, x

(S), is feasible if

it allocates no item more than once, i.e.,for all j ∈ M,

∑

i∈N

∑

S∋ j

(S) ≤ 1

The winner determination problem is the problem to

maximize total revenue. For feasible allocations X ∋

(S),

max

∑

i∈N,S⊆M

(S)x

(S)

Here, we used simple OR-bids representation as

our bidding language. Substitutability can be rep-

resented by a set of atomic OR-bids with dummy

items(Cramton et al., 2006).

Even when we only focus on utility-based re-

source allocation problems, they enforce us to solve

winner determination problem with really hard-time

constraint for realizing ﬁne-grained resource alloca-

tion. Here, we have to consider that, in such resource

allocation procedures, we need to spend much time

for pricing and communications for actual resource

allocation protocols. Therefore, we need a fast win-

ner determination algorithm for auctions with a large

number of bids. In this paper, primarily we focus on

solving this problem.

2.2 Lehmann’s Greedy Winner

Determination

Lehmann’s greedy algorithm (Lehmann et al., 2002)

is a very simple but powerful linear algorithm for win-

ner determination on combinatorial auctions. Here, a

bidder declaring < s,a >, with s ⊆ M and a ∈ R

will be said to put out a bid b =< s,a >. Two bids

b =< s,a > and b

′

=< s

′

> conﬂict iff s∩ s

′

The greedy algorithm can be described as follows:

(1) The list of bids L is sorted by some criterion. In

(Lehmann et al., 2002), a method to sort the list L

by descending average amount per item is proposed.

APPROXIMATED WINNER DETERMINATION FOR A SERIES OF COMBINATORIAL AUCTIONS

401

More generally, they proposed sorting L by a crite-

rion of the form a/|s|

for some number c ≥ 0, which

possibly depends on the number of items, m. (2) A

greedy algorithm generates an allocation. L is the

sorted list in the ﬁrst phase. The algorithm walk down

the list L, accepting bids if the items demanded are

still unallocated and unconﬂicted.

In (Lehmann et al., 2002), Lehmann et, al . ar-

gued that c = 1/2 is the best parameter for approxi-

mation when the norm of the worst case performance

is considered

. Also they showed that the mechanism

is truthful when single-minded bidders are assumed

and their proposed pricing scheme is used.

2.3 Hill-climbing Search

In (Fukuta and Ito, 2006)we proposed a preliminary

idea of our hill-climbing approach, and in (Fukuta

and Ito, 2007a)we showedour hill-climbing approach

performs well when an auction has an enormous num-

ber of bids. In this section, we summarize our pro-

posed algorithms.

Lehmann’s greedy winner determination typically

performs well and the lower bound of the optimality

has been analyzed(Lehmann et al., 2002). A straight-

forward extension of the greedy algorithm is to con-

struct a local search algorithm that continuously up-

dates the allocation to increase optimality. Intuitively,

one allocation corresponds to one state of a local

search.

The inputs are Alloc and L. L is the bid list of an

auction. Alloc is the initial greedy allocation of items

for the bid list.

1: function LocalSearch(Alloc, L)

2: RemainBids:= L∩ Alloc;

3: for each b ∈ RemainBids as sorted order

4: if b conﬂicts Alloc then

5: Conflicted:=Alloc∩ consistentBids({b},Alloc);

6: NewAlloc:= (Alloc ∩Con flicted) ∪ {b};

7: ConsBids:=

8: consistentBids(NewAlloc, RemainBids);

9: NewAlloc:=NewAlloc ∪ConsBids;

10: if price(Alloc) < price(NewAlloc) then

11: return LocalSearch(NewAlloc,L);

12: end for each

13: return Alloc

Function consistentBids ﬁnds consistent bids for the

set NewAlloc by walking down the list RemainBids.

Note that, in (Sandholm et al., 2005), Sandholm et,al.

determined experimentally that c ∈ [0.8,1] yields best per-

formance in their approach.

Here, since a new inserted bid will wipe out some bids

that are conﬂicting with the inserted bid, free items

will appear to be allocated to other bidders after the

insertion. Function consistentBids tries to ﬁnd out po-

tential winner bids that do not conﬂict to the speciﬁed

allocation.

2.4 Parallel Search for Multiple

Weighting

The optimality of allocations obtained by Lehmann’s

algorithm (and the subsequent hill-climbing) deeply

depends on which value was set to c in the bid weight-

ing function. Lehmann et al. reported that c = 1/2

guarantees lower bound of approximation. However,

the optimal values for each auction are varied from 0

to 1 depending on the auction problem.

In (Fukuta and Ito, 2006), an enhancement has

been presented for local search algorithm to paral-

lel search for different bid weighting strategies (e.g.,

doing the same algorithm for both c = 0 and c = 1)

In the algorithm, the value of c for Lehmann’s al-

gorithm is selected from a pre-deﬁned list. Select-

ing c from neighbors of 1/2 is reasonable, namely,

C = {0.0,0.1, . . .,1.0}. The results are aggregated

and the best one (with the highest revenue) is selected

as the ﬁnal result.

2.5 Other Approximation Approaches

Zurel and Nisan(Zurel and Nisan, 2001) proposed

a very high performance approximate winner deter-

mination algorithm for combinatorial auctions. The

main idea is a combination of approximated positive

linear program algorithm for determining initial allo-

cation and stepwise random updates of allocations.

Hoos(Hoos and Boutilier, 2000) proposed

Casanova algorithm, and showed that a generic

random walk SAT solver may perform well for ap-

proximation of combinatorial auctions. It is based on

scoring each search state using the revenue-per-item

of the corresponding allocation.

3 ENHANCED APPROXIMATION

3.1 Fast Partial Reallocation by Last

Result

In the setting of the periodical resource re-allocation

scenario, winner determination occurs when some

bids are revised. Theoretically, we need to recalcu-

late winners even if only one bid is changed in the

ICAART 2009 - International Conference on Agents and Artificial Intelligence

402

auction. However, in some cases, reusing the win-

ners of previous auctions is useful when the change is

small so that it has small effects to the next winner de-

termination process. The following simple algorithm

reuses the approximation result of the last cycle when

recalculation is needed due to changes of the

Here, we assume that the bids won at the last cy-

cle (LastWinners) and the all bids at the last cycle

(LastBids) are known.

1: Function PartialReallocationA(

2: LastBids,LastWinners,CurrentBids)

3: AddedBids :=

4: CurrentBids∩ (LastBids∩CurrentBids);

5: DeletedBids :=

6: LastBids∩ (LastBids∩CurrentBids);

7: Winners := LastWinners;

8: foreach d ∈ DeletedBids

9: if d ∈ Winners

10: then Winners := Winners∩ {d};

11: foreach a ∈ AddedBids

12: foreach w ∈ Winners

13: if w and a are bids placed for the exactly same items

14: and price({w}) < price({a})

15: then Winners := (Winners∩ {w}) ∪{a};

16: Winners := LocalSearch(Winners,CurrentBids);

17: return Winners

First, the algorithm deletes winners that no longer

valid due to deletion of bids. Then, some winner bids

are replaced by newly added bids. Note that we only

replace a bid when the bids are placed for exactly the

same items, i.e., for two bids b

(X) and b

(Y), X = Y,

to avoid the ordering problem of newly added bids.

Modiﬁcation of a bid through cycles is treated as a

combined operation of the deletion of previous bid

and the addition of the renewed bid.

3.2 Eliminating Undesirable

Reallocations

Generally speaking, the performance of reusing the

partial results of similar problems depends on the

problem. Therefore, in some cases, reusing the last

result may cause performance decreases. To avoid

such a situation, we slightly modiﬁed our algorithm

to switch the initial allocation by evaluating its per-

formance.

Here, the modiﬁed algorithm simply compares the

reused result with greedy allocation. Then, the bet-

ter one is used as the seed of hill-climbing improve-

ment. Note that both our reallocation and greedy al-

location algorithms complete their executions in very

short time. Therefore, computational overhead for

them is expected to be negligible.

1: Function PartialReallocationX(

2: LastBids,LastWinners,CurrentBids)

3: AddedBids :=

4: CurrentBids∩ (LastBids∩CurrentBids);

5: DeletedBids :=

6: LastBids∩ (LastBids∩CurrentBids);

7: Winners := LastWinners;

8: foreach d ∈ DeletedBids

9: if d ∈ Winners

10: then Winners := Winners∩ {d};

11: foreach a ∈ AddedBids

12: foreach w ∈ Winners

13: if w and a are bids placed for the exactly same items

14: and price({w}) < price({a})

15: then Winners := (Winners ∩ {w}) ∪{a};

16: GreedyWinners := GreedySearch(CurrentBids);

17: if price(Winners) ≤ price(GreedyWinners)

18: then Winners := GreedyWinners;

19: Winners := LocalSearch(Winners,CurrentBids);

20: return Winners

4 EVALUATION

4.1 Experiment Settings

We implemented our algorithms in a C program for

the following experiments. We also implemented the

Casanova algorithm in a C program. For Zurel’s al-

gorithm, we used Zurel’s C++ based implementation

that is shown in (Zurel and Nisan, 2001). Also we

used CPLEX Interactive Optimizer 11.0.0 (32bit) in

our experiments

. The experiments were done with

above implementations to examine the performance

differences among algorithms. The programs were

employed on a Mac with Mac OS X 10.4, a CoreDuo

2.0GHz CPU, and 2GBytes of memory.

We conducted several experiments. In each ex-

periment, we compared the following search algo-

rithms: greedy(C=0.5) uses Lehmann’s greedy allo-

cation algorithm with parameter (c = 0.5). greedy-3

uses the best results of Lehmann’s greedy allocation

algorithm with parameter (0 ≤ c ≤ 1 in 0.5 steps).

HC(c=0.5) uses a local search in which the initial allo-

cation is Lehmann’s allocation with c = 0.5 and con-

ducts the hill-climbing search shown in section 2.3.

Although CPLEX is an optimizer that can obtain opti-

mal results, it is reported in (Sandholm et al., 2005) that its

anytime approximation performance is also good.

APPROXIMATED WINNER DETERMINATION FOR A SERIES OF COMBINATORIAL AUCTIONS

403

HC-3 uses the best results of the hill-climbing search

with parameter (0 ≤ c ≤ 1 in 0.5 steps). We denote

the Casanova algorithm as casanova and Zurel’s al-

gorithm as Zurel Also we denote results of 1st stage

of Zurel’s algorithm as Zurel-1st. Note that Zurel’s

algorithm does not produce any approximation result

until completing its 1st stage. cplex is the result of

CPLEX with the speciﬁed time limit.

In the following experiments, we used 0.2 for the

epsilon value of Zurel’s algorithm. This value appears

in (Zurel and Nisan, 2001). Also we used 0.5 for np

and 0.15 for wp on Casanova that appear in (Hoos

and Boutilier, 2000). Note that we set maxTrial to 1

but maxSteps to ten times the number of bids in the

auction.

We conducted detailed comparisons among our

past presented algorithms and the other existing al-

gorithms mentioned above. The details of the com-

parisons are shown in (Fukuta and Ito, 2007b) and

(Fukuta and Ito, 2007a). In (Fukuta and Ito, 2007b)

and (Fukuta and Ito, 2007a), we prepared datasets

with 20,000 bids in an auction. The datasets were

produced by CATS(Leyton-Brown et al., 2000) with

default parameters in 5 different distributions. They

contain 100 trials for each distribution. Each trial is

an auction problem with 256 items and 20,000 bids.

However, since CATS common datasets only pro-

vide static bids for an auction, we prepared ex-

tended usage for those datasets to include the dynamic

changes of bids in an auction.

Procedure: In each auction, the bid set is di-

vided into k blocks by the order of bid generation (i.e.,

bid id). The bid set is modiﬁed totally k times and the

modiﬁcation is done in each second. In each 1-second

period, a block is marked as hidden so that bids within

these marked blocks are treated as deleted bids. For

example, at the ﬁrst period, the ﬁrst block is marked

as hidden so the remaining bids (second to kth blocks)

are used for winner determination. After 1 second, the

mark is moved to the second block (i.e., the ﬁrst, and

the third to kth blocks are used) and the winner deter-

mination process is restarted due to this change. Here,

we can see it as the bids in the ﬁrst block are newly

added to the auction and the bids in the second block

are deleted from the auction. This process is repeated

until the mark has been moved to the kth block. Fi-

nally, all marks are cleared and the winner determina-

tion process is restarted with full bids in the auction.

Ordinary algorithms should be completely restarted in

each cycle. However, when we use our proposed real-

location algorithms, some intermediate results can be

Due to difﬁculty of dataset preparation, we only pre-

pared ﬁve distributions. Producing a dataset with other dis-

tributions is difﬁcult in feasible time.

reused in the next cycle in the same auction.

Since the bid set in the k + 1th cycle completely

equals the bids of the auction, the results of the k+1th

cycle can be compared to our previous experimental

results.

4.2 Time Performance

Table 1 shows the experimental result on the datasets

with 20,000 bids in an auction focused on execution

time of approximation. Due to the difﬁculty of at-

taining optimal values, we normalized all values as

Zurel’s results equal 1 as follows.

Let A be a set of algorithms, z ∈ A be the zurel’s

approximation algorithm, D be a dataset generated for

this experiment, and revenue

(p) such that a ∈ A be

the revenue obtained by algorithm a for a problem p

in a dataset, the average revenue ratio rationA

(D) for

algorithm a ∈ A for dataset D is deﬁned as follows:

ratioA

(D) =

∑

p∈D

revenue

(p)

∑

p∈D

revenue

(p)

Here, we use ratioA

(D) for our comparison of algo-

rithms.

The name of each distribution is taken from

(Leyton-Brown et al., 2000). We prepared the cut-off

results of Casanova and HC. For example, casanova-

10ms denotes the results of Casanova within 10 mil-

liseconds. Also we prepared a variant of our algo-

rithm that has a sufﬁx of -seq or -para. The sufﬁx -seq

denotes that the algorithm is completely executed se-

quentially that is equal to be executed on a single CPU

computer. For example, greedy-3-seq denotes that the

execution time is the sum of execution times spent by

three threads. The sufﬁx -para denotes that the algo-

rithm is completely executed in a parallel manner, the

three independent threads are completely executed in

parallel. Here, we used ideal value for -para since

our computer has only two cores in the CPU. The ac-

tual execution performance will be between -seq and

-para.

Additionally, we added results with names AHC or

XHC in the same table. They are the average approxi-

mated results of the k+ 1th cycle of auctions with our

proposed algorithms

PartialReallocationA

and

PartialReallocationX

, respectively.

In most distributions, Zurel-1st takes more than

one second but the obtained optimality is lower than

greedy-3-seq. However, our proposed HC-3 performs

better or slightly lower although their computation

times are shorter than Zurel-1st and Zurel, excluding

L3. Surprisingly, in most cases, the results of XHC-

3-seq-100ms are better than HC-3-seq-1000ms while

their spent computation time is only 1/10. This fact

ICAART 2009 - International Conference on Agents and Artificial Intelligence

404

Table 1: Time Performance of (k+1)th cycle on 20,000bids-256items (k=10).

L2 L3 L4 L6 L7 average

greedy(c=0.5) 1.0002 (23.0) 0.9639 (19.0) 0.9417 (23.0) 0.9389 (23.4) 0.7403 (22.1) 0.9170 (22.1)

greedy-3-seq 1.0003 (69.1) 0.9639 (59.2) 0.9999 (72.9) 0.9965 (67.8) 0.7541 (66.8) 0.9429 (67.2)

greedy-3-para 1.0003 (26.4) 0.9639 (20.9) 0.9999 (28.4) 0.9965 (26.0) 0.7541 (25.5) 0.9429 (25.4)

HC(c=0.5)-100ms 1.0004 (100) 0.9741 (100) 0.9576 (100) 0.9533 (100) 0.8260 (100) 0.9423 (100)

HC-3-seq-100ms 1.0004 (100) 0.9692 (100) 1.0000 (100) 0.9966 (100) 0.8287 (100) 0.9590 (100)

AHC-3-seq-100ms 1.0004 (100) 0.9690 (100) 1.0006 (100) 0.9974 (100) 1.0225 (100) 0.9980 (100)

XHC-3-seq-100ms 1.0004 (100) 0.9813 (100) 1.0005 (100) 0.9987 (100) 1.0217 (100) 1.0005 (100)

HC-3-para-100ms 1.0004 (100) 0.9743 (100) 1.0001 (100) 0.9969 (100) 0.9423 (100) 0.9828 (100)

AHC-3-para-100ms 1.0004 (100) 0.9741 (100) 1.0006 (100) 0.9977 (100) 1.0249 (100) 0.9995 (100)

XHC-3-para-100ms 1.0004 (100) 0.9820 (100) 1.0006 (100) 0.9988 (100) 1.0249 (100) 1.0013 (100)

HC(c=0.5)-1000ms 1.0004 (1000) 0.9856 (1000) 0.9771 (1000) 0.9646 (1000) 1.0157 (1000) 0.9887 (1000)

HC-3-seq-1000ms 1.0004 (1000) 0.9804 (1000) 1.0003 (1000) 0.9976 (1000) 1.0086 (1000) 0.9975 (1000)

AHC-3-seq-1000ms 1.0004 (1000) 0.9795 (1000) 1.0007 (1000) 0.9982 (1000) 1.0266 (1000) 1.0011 (1000)

XHC-3-seq-1000ms 1.0004 (1000) 0.9830 (1000) 1.0006 (1000) 0.9991 (1000) 1.0266 (1000) 1.0019 (1000)

HC-3-para-1000ms 1.0004 (1000) 0.9856 (1000) 1.0006 (1000) 0.9987 (1000) 1.0240 (1000) 1.0019 (1000)

AHC-3-para-1000ms 1.0004 (1000) 0.9847 (1000) 1.0008 (1000) 0.9990 (1000) 1.0272 (1000) 1.0024 (1000)

XHC-3-para-1000ms 1.0004 (1000) 0.9853 (1000) 1.0008 (1000) 0.9996 (1000) 1.0272 (1000) 1.0027 (1000)

Zurel-1st 0.5710 (11040) 0.9690 (537) 0.9983 (2075) 0.9928 (1715) 0.6015 (1796) 0.8265 (3433)

Zurel 1.0000 (13837) 1.0000 (890) 1.0000 (4581) 1.0000 (4324) 1.0000 (3720) 1.0000 (5470)

casanova-10ms 0.2583 (10) 0.0069 (10) 0.0105 (10) 0.0202 (10) 0.2577 (10) 0.0632 (10)

casanova-100ms 0.2583 (100) 0.0069 (100) 0.0105 (100) 0.0202 (100) 0.2577 (100) 0.1107 (100)

casanova-1000ms 0.5357 (1000) 0.1208 (1000) 0.0861 (1000) 0.1486 (1000) 0.7614 (1000) 0.3305 (1000)

cplex-100ms 0.0000 (288) 0.0000 (121) 0.0299 (111) 0.0000 (150) 0.0000 (119) 0.0060 (158)

cplex-333ms 0.0000 (489) 0.0000 (393) 0.9960 (497) 0.9716 (354) 0.0000 (487) 0.3935 (444)

cplex-1000ms 0.0000 (1052) 0.0000 (1039) 0.9960 (1143) 0.9716 (1140) 0.0000 (2887) 0.3935 (1452)

cplex-3000ms 0.0000 (9171) 0.9338 (3563) 0.9964 (3030) 0.9716 (3077) 0.0000 (3090) 0.5804 (4386)

(each value in () is time in milliseconds)

shows that our XHC-3 could effectively reuse the ap-

proximated results of previous cycles.

In many settings of CPLEX, the values are 0. This

is because CPLEX could not generate initial approxi-

mation result within the provided time limit. Only L4

and L6 have results for CPLEX. For them, CPLEX

spends around 400 msec for the computation but the

results are still lower than greedy-3. For L3, CPLEX

could prepare results in 3.8 sec of computation, how-

ever, the result is still lower than greedy-3. This is

because the condition we set up gave extremely short

time limit so therefore CPLEX could not generate suf-

ﬁcient approximation results in such hard time con-

straint.

Table 2 shows the experimental result on the

datasets with 100,000 bids in an auction focused on

execution time of the approximation. The settings are

identical as Table 1 excluding the difference of num-

ber of bids in an auction. Due to hard time constraint,

results of -seq-100ms (sequential execution with a

cutoff time of 100ms) are excluded from the table

since they could not complete their execution within

the cutoff time. Here, our proposed methods (AHC-

3,XHC-3) clearly have a certain advantage of their

performance time ratio. HC-3,AHC-3,and XHC-3 pro-

duced acceptable approximated results within 100 to

1000 msec that are 2 to 443 times faster than Zurel’s

approximation. Especially, in most cases, our AHC-3-

para-100ms outperforms HC-3-seq-1000ms and HC-

3-para-1000ms.

On above experiments, we used k = 10. Table 3

shows average time performance of our algorithms on

k = 2,5,10,20, 40, respectively. At same cutoff time,

XHC-3 obtains higher or at least same performance

compared to HC-3. Furthermore, XHC-3-para-100ms

outperforms HC-3-para-1000ms when k ≥ 20, while

its computation time is 10 times shorter.

On above experiments, for direct comparison to

other existing algorithms, we have shown results on

ﬁnal(e.g., (k + 1)th) cycle in our procedure. We also

conﬁrmed performance improvement on intermediate

cycle in our procedure. Table 4 shows average re-

sults on intermediate cycles for three algorithms (HC-

3,AHC-3,and XHC-3). Here, since we do not have ap-

proximation results for those intermediate cycles on

Zurel’s algorithm, instead of using ratioA, we nor-

malized all values as HC-3-para-1000msec equals 1.

Since our algorithms improve results much more for

latter cycles by cumulative reuse of the last cycle, we

used ﬁrst four cycles in this comparison. For results

on k = 5,10,20,40, we used an average value for ﬁrst

four intermediate cycles (e.g., from 2nd to 5th). Note

APPROXIMATED WINNER DETERMINATION FOR A SERIES OF COMBINATORIAL AUCTIONS

405

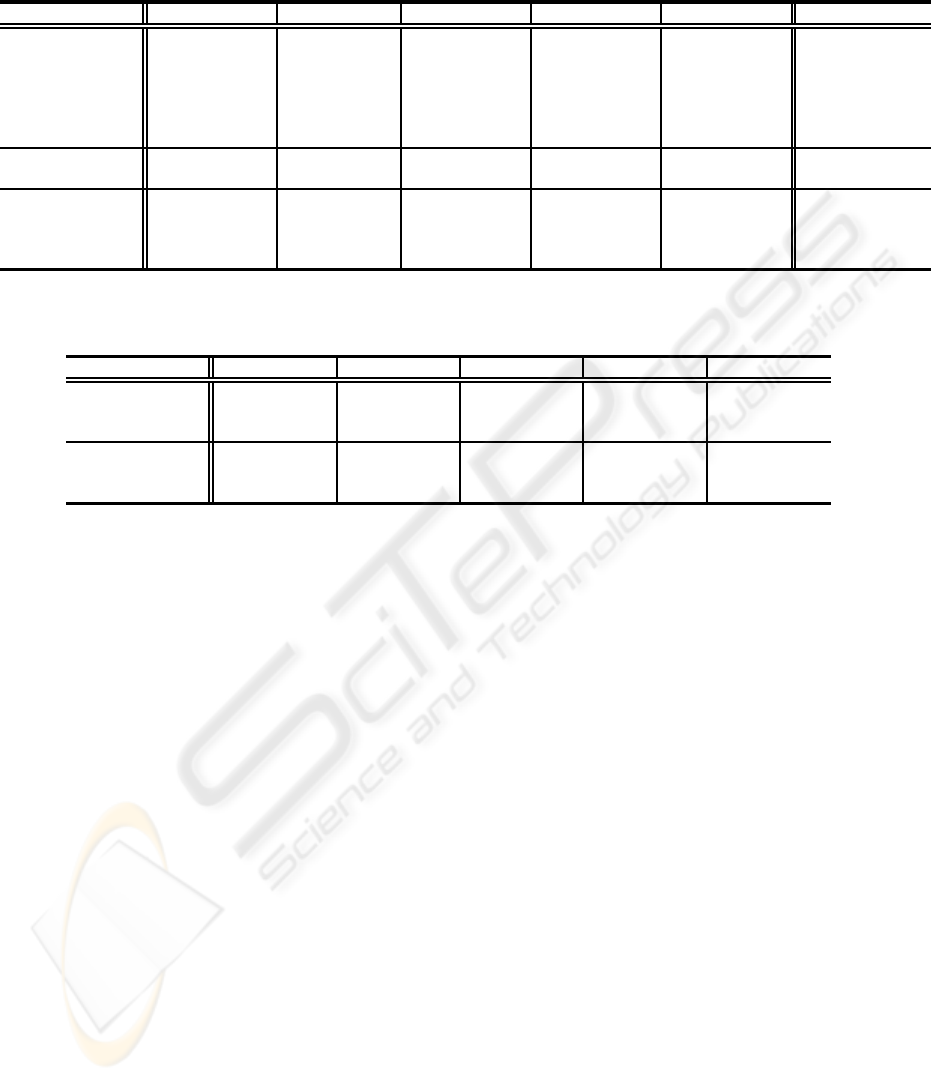
Table 2: Time Performance of (k+1)th cycle on 100,000bids-256items (k=10).

L2 L3 L4 L6 L7 average

HC-3-para-100ms 1.1098 (100) 0.9836 (100) 1.0003 (100) 1.0009 (100) 0.8688 (100) 0.9927 (100)

AHC-3-para-100ms 1.1098 (100) 0.9836 (100) 1.0003 (100) 1.0009 (100) 0.9941 (100) 1.0177 (100)

XHC-3-para-100ms 1.1098 (100) 0.9880 (100) 1.0003 (100) 1.0010 (100) 0.9939 (100) 1.0186 (100)

HC-3-para-1000ms 1.1098 (1000) 0.9880 (1000) 1.0003 (1000) 1.0010 (1000) 0.9814 (1000) 1.0161 (1000)

AHC-3-para-1000ms 1.1098 (1000) 0.9880 (1000) 1.0003 (1000) 1.0010 (1000) 0.9991 (1000) 1.0197 (1000)

XHC-3-para-1000ms 1.1098 (1000) 0.9889 (1000) 1.0003 (1000) 1.0011 (1000) 0.9990 (1000) 1.0198 (1000)

zurel-1st 0.8971 (74943) 0.9827 (2257) 0.9998 (5345) 0.9987 (4707) 0.7086 (8688) 0.9174 (19188)

Zurel 1.0000 (91100) 1.0000 (6036) 1.0000 (30568) 1.0000 (44255) 1.0000 (17691) 1.0000 (37930)

cplex-100ms 0.0000 (2022) 0.0000 (232) 0.0000 (143) 0.0000 (133) 0.0000 (852) 0.0000 (676)

cplex-333ms 0.0000 (2021) 0.0000 (559) 0.9998 (1084) 0.0000 (412) 0.0000 (852) 0.2000 (986)

cplex-1000ms 0.0000 (2021) 0.0000 (1045) 0.9998 (1085) 0.0000 (1328) 0.0000 (1285) 0.2000 (1353)

cplex-3000ms 0.0000 (3496) 0.0000 (3286) 0.9998 (5207) 0.9965 (3092) 0.0000 (15667) 0.3993 (6149)

(each value in () is time in milliseconds)

Table 3: Time Performance of (k+1)th cycle on 20,000bids-256items (k=2,5,10,20,40).

k=2 k=5 k=10 k=20 k=40

HC-3-para-100ms 0.9828 (100) 0.9828 (100) 0.9828 (100) 0.9828 (100) 0.9828 (100)

AHC-3-para-100ms 0.9952 (100) 0.9979 (100) 0.9995 (100) 1.0003 (100) 1.0009 (100)

XHC-3-para-100ms 0.9952 (100) 0.9998 (100) 1.0013 (100) 1.0021 (100) 1.0028 (100)

HC-3-para-1000ms 1.0019 (1000) 1.0019 (1000) 1.0019 (1000) 1.0019 (1000) 1.0019 (1000)

AHC-3-para-1000ms 1.0019 (1000) 1.0021 (1000) 1.0024 (1000) 1.0026 (1000) 1.0027 (1000)

XHC-3-para-1000ms 1.0019 (1000) 1.0025 (1000) 1.0027 (1000) 1.0031 (1000) 1.0035 (1000)

(each value in () is time in milliseconds)

that, only for results on k = 2, we used the results on

2nd cycle since we do not have other intermediate cy-

cles when k = 2. Here, results of XHC-3 constantly

better than AHC-3 and HC-3 and the differences are

bigger when k is increased.

5 RELATED WORK

There have been a lot of works on the optimal algo-

rithms for winner determination in combinatorial auc-

tions(de Vries and Vohra, 2003). Recently, Dobzinski

et, al. proposed improved approximation algorithms

for auctions with submodular bidders(Dobzinski and

Schapira, 2006). Lavi et, al, reported an LP based

algorithm that can be extended to support the clas-

sic VCG(Lavi and Swamy, 2005). Those researches

are mainly focused on theoretical aspects. In con-

trast to those papers, we rather focus on experimen-

tal and implementation aspects. Those papers did not

present experimental analysis about the settings with

large number of bids we presented in this paper. Also,

Guo(Guo et al., 2005) proposed local-search based al-

gorithms for large number of bids in combinatorial

auction problems. However, they did not present ex-

periments with such a huge number of bids we used

in our experiments.

CPLEX is a well-known,very fast linear program-

ming solver system. In (Zurel and Nisan, 2001), Zurel

et al. evaluated the performance of their presented al-

gorithm with many data sets, compared with CPLEX

and other existing implementations. While the ver-

sion of CPLEX used in (Zurel and Nisan, 2001) is

not up-to-date, the shown performance of Zurel’s al-

gorithm is approximately 10 to 100 times faster than

CPLEX. In this paper, we showed direct compar-

isons to the latest version of CPLEX we could pre-

pare. Our approach is far better than latest version

of CPLEX for large-scale winner determination prob-

lems. Therefore, the performance of our approach is

better than CPLEX in our settings. This is natural

since Zurel’s and our approaches are specialized for

combinatorial auctions, and also focus only on faster

approximation but do not seek optimal solutions. In

case we need optimal solutions, it is good choice to

solve the same problem by both our approach and

CPLEX in parallel.

The above approaches are based on ofﬂine algo-

rithms and therefore there are no considerations about

addition and deletion of bids in their approximation

processes. Although our algorithms are not strict on-

line algorithms, it is possible to reuse the last results

when bids are modiﬁed and recalculation is necessary.

ICAART 2009 - International Conference on Agents and Artificial Intelligence

406

Table 4: Time Performance of intermediate cycles on 20,000bids-256items (k=2,5,10,20,40).

k=2 k=5 k=10 K=20 K=40

HC-3-para-100ms 0.9889 0.9847 0.9829 0.9826 0.9818

AHC-3-para-100ms 0.9889 0.9805 0.9838 0.9874 0.9897

XHC-3-para-100ms 0.9892 0.9917 0.9943 0.9951 0.9966

(values are normalized as HC-3-para-1000msec equals 1)

6 CONCLUSIONS

In this paper, we proposed enhanced approximation

algorithms for combinatorial auctions that are suitable

for the purpose of iterative reallocation of items. Our

proposed algorithms effectively reuse the last solu-

tions to speed up initial approximation performance.

The experimentalresults showed that our proposed al-

gorithms outperform existing algorithms in some as-

pects. However, we found that in some cases reusing

the last solutions may worsen performance compared

to ordinary approximation from scratch. We proposed

an enhanced algorithm that effectively avoids the un-

desirable reuse of the last solutions in the algorithm.

We showed this is especially effective when a non-

negligible number of existing bids are deleted from

the last cycle.

REFERENCES

Andrew, L. L., Hanly, S. V., and Mukhtar, R. G. (2008).

Active queue management for fair resource allocation

in wireless networks. IEEE Transactions on Mobile

Computing, pages 231–246.

Cramton, P., Shoham, Y., and Steinberg, R. (2006). Combi-

natorial Auctions. The MIT Press.

de Vries, S. and Vohra, R. V. (2003). Combinatorial auc-

tions: A survey. International Transactions in Opera-

tional Research, 15(3):284–309.

Dobzinski, S. and Schapira, M. (2006). An improved

approximation algorithm for combinatorial auctions

with submodular bidders. In Proc. of the seven-

teenth annual ACM-SIAM symposium on Discrete al-

gorithm(SODA2006), pages 1064–1073. ACM Press.

Fujishima, Y., Leyton-Brown, K., and Shoham, Y. (1999).

Taming the computational complexity of combinato-

rial auctions: Optimal and approximate approarches.

In Proc. of the 16th International Joint Conference on

Artiﬁcial Intelligence (IJCAI1999), pages 548–553.

Fukuta, N. and Ito, T. (2006). Towards better approxima-

tion of winner determination for combinatorial auc-

tions with large number of bids. In Proc. of The 2006

WIC/IEEE/ACM International Conference on Intelli-

gent Agent Technology(IAT2006), pages 618–621.

Fukuta, N. and Ito, T. (2007a). Periodical resource allo-

cation using approximated combinatorial auctions. In

Proc. of The 2007 WIC/IEEE/ACMInternational Con-

ference on Intelligent Agent Technology(IAT2007),

pages 434–441.

Fukuta, N. and Ito, T. (2007b). Short-time approximation

on combinatorial auctions – a comparison on approx-

imated winner determination algorithms. In Proc. of

The 3rd International Workshop on Data Engineering

Issues in E-Commerce and Services(DEECS2007),

pages 42–55.

Guo, Y., Lim, A., Rodrigues, B., and Zhu, Y. (2005).

A non-exact approach and experiment studies on

the combinatorial auction problem. In Proc. of the

38th Hawaii International Conference on System Sci-

ences(HICSS2005), page 82.1.

Hoos, H. H. and Boutilier, C. (2000). Solving combinato-

rial auctions using stochastic local search. In Proc.

of the Proc. of 17th National Conference on Artiﬁcial

Intelligence (AAAI2000), pages 22–29.

Lavi, R. and Swamy, C. (2005). Truthful and near-optimal

mechanism design via linear programming. In 46th

Annual IEEE Symposium on Foundations of Computer

Science (FOCS2005), pages 595–604.

Lehmann, D., O’Callaghan, L. I., and Shoham, Y. (2002).

Truth revelation in rapid, approximately efﬁcient com-

binatorial auctions. Journal of the ACM, 49:577–602.

Leyton-Brown, K., Pearson, M., and Shoham, Y. (2000).

Towards a universal test suite for combinatorial auc-

tion algorithms. In Proc. of ACM Conference on Elec-

tronic Commerce (EC2000), pages 66–76.

McMillan, J. (1994). Selling spectrum rights. The Journal

of Economic Perspectives.

Sandholm, T. (2007). Expressive commerce and its ap-

plication to sourcing: How we conducted $35 billion

of generalized combinatorial auctions. AI Magazine,

28(3):45–58.

Sandholm, T., Suri, S., Gilpin, A., and Levine, D. (2005).

Cabob: A fast optimal algorithm for winner determi-

nation in combinatorial auctions. Management Sci-

ence, 51(3):374–390.

Thomadakis, M. E. and Liu, J.-C. (1999). On the efﬁcient

scheduling of non-periodic tasks in hard real-time sys-

tems. In Proc. of IEEE Real-Time Systems Symp.,

pages 148–151.

Xiao, L., Chen, S., and Zhang, X. (2004). Adaptive memory

allocations in clusters to handle unexpectedly large

data-intensive jobs. IEEE Transactions on Parallel

and Distributed Systems, 15(7):577–592.

Xie, T. and Qin, X. (2008). Security-aware resource allo-

cation for real-time parallel jobs on homogeneous and

heterogeneous clusters. IEEE Transactions on Paral-

lel and Distributed Systems, 19(5):682–697.

Zurel, E. and Nisan, N. (2001). An efﬁcient approximate

allocation algorithm for combinatorial auctions. In

Proc. of the Third ACM Conference on Electronic

Commerce (EC2001), pages 125–136.

APPROXIMATED WINNER DETERMINATION FOR A SERIES OF COMBINATORIAL AUCTIONS

407