GOAL-BASED ADVERSARIAL SEARCH

Searching Game Trees in Complex Domains using Goal-based Heuristic

Viliam Lis

y, Branislav Bo

sansk

y, Michal Jakob and Michal P

echou

cek

Agent Technology Center, Department of Cybernetics, Faculty of Electrical Engineering

Czech Technical University in Prague, Czech Republic

Keywords:

Game tree search, Adversarial planning, Goals, Background knowledge, Complex domain.

Abstract:

We present a novel approach to reducing adversarial search space by using background knowledge represented

in the form of higher-level goals that players tend to pursue in the game. The algorithm is derived from a

simultaneous-move modiﬁcation of the max

algorithm by only searching the branches of the game tree that

are consistent with pursuing player’s goals. The algorithm has been tested on a real-world-based scenario

modelled as a large-scale asymmetric game. The experimental results obtained indicate the ability of the goal-

based heuristic to reduce the search space to a manageable level even in complex domains while maintaining

the high quality of resulting strategies.

1 INTRODUCTION

Recently, there has been a growing interest in study-

ing complex systems in which large numbers of

agents concurrently pursue their goals while engag-

ing in complicated patterns of mutual interaction. Ex-

amples include real-world systems, such as various

information and communication networks or social

networking applications as well as simulations, in-

cluding models of societies, economies and/or war-

fare. Because in most such systems the agents are

part of a single shared environment, situations arise in

which their actions and strategies interact. Such situ-

ations, in which the outcome of agent’s actions de-

pends on actions chosen by others, are often termed

games and have been an interest of AI research from

its very beginning. With the increasing complexity of

the environments in which the agents interact, how-

ever, classical game playing algorithms, such as mini-

max search, become unusable due to the huge branch-

ing factor, size of the state space, continuous time and

space, and other factors.

In this paper, we present a novel game tree search

algorithm adapted and extended for use in large-scale

multi-player games with asymmetric objectives (non-

zero-sum games). The basis of the proposed algo-

rithm is the max

algorithm (Luckhardt and K.B.Irani,

1986) generalized to simultaneous moves. The main

contribution, however, lies in a novel way in which

background knowledge about possible player’s goals

and the conditions under which they are adopted is

represented and utilized in order to reduce the extent

of game tree search. The background knowledge con-

tains:

• Goals corresponding to basic objectives in the

game (goals represent elementary building blocks

of player’s strategies); each goal is associated with

an algorithm which decomposes it into a sequence

of actions leading to its fulﬁlment.

• Conditions deﬁning world states in which pursu-

ing the goals is meaningful (optionally, represent-

ing conditions deﬁning when individual players

might pursue the goals).

• Evaluation function assigning to each player and

world state a numeric value representing desir-

ability of the game state for the player (e.g. utility

of the state for the player).

The overall background knowledge utilized in the

search can be split into a player-independent part (also

termed domain knowledge) and a player-speciﬁc part

(further termed opponent models).

The proposed approach builds on the assumption

that strategies of the players in the game are com-

posed from higher-level goals rather than from ar-

bitrary sequences of low-level actions. Adapted in

game tree search, this assumption brings considerably

smaller game trees, because it allows evaluating only

those branches of low-level actions that lead to reach-

ing some higher-level goal. However, as with almost

Lisý V., Bošanský B., Jakob M. and P

echou

cek M. (2009).

GOAL-BASED ADVERSARIAL SEARCH - Searching Game Trees in Complex Domains using Goal-based Heuristic.

In Proceedings of the International Conference on Agents and Artiﬁcial Intelligence, pages 53-60

DOI: 10.5220/0001659900530060

 SciTePress

any kind of heuristics, the reduction in computational

complexity can potentially decrease the quality of re-

sulting strategies, and this fundamental trade-off is

therefore an important part of algorithm’s evaluation

described further in the paper.

The next section introduces the challenges that

complicate using game-tree search in complex do-

mains. Section 3 describes the proposed algorithm

designed to address them. Search space reduction,

precision loss and scalability of the algorithm are ex-

perimentally examined in Section 4. Section 5 re-

views the related work and the paper ends with con-

clusions and discussion of future research.

2 CHALLENGES

The complex domains of our interest include real-

world domains like network security or military op-

erations. We use the later for intuition in this sec-

tion. The games appearing there are often n-player

non-zero-sum games with several conceptual prob-

lems that generally prohibit using classic game-tree

search algorithms, such as max

• Huge branching factor (BF) – In contrast to

many classical games, in military operations the

player assign actions simultaneously to all units

it controls. Together with a higher number of ac-

tions (including parameters) which the units can

perform, this results in branching factors several

magnitudes bigger than in games such as Chess

(BF ≈ 35) or Go (BF ≈ 361).

• Importance of long plans – In many realis-

tic scenarios, long sequence of atomic actions is

needed before a signiﬁcant change to the state of

world/game is produced. A standard game tree

in such scenarios needs to use a correspondingly

high search depth, further aggravating the effect

of huge branching factor mentioned earlier.

Let us emphasis also the advantages that using

game tree search can bring. If we successfully over-

come the mentioned problems, we can reuse the large

amount of research in this area and further enhance

the searching algorithm with many of existing ex-

tensions (such as use of various opponent models,

probabilistic extensions, transposition tables, or other

shown e.g. in (Schaeffer, 1989)).

3 GOAL-BASED GAME-TREE

In this section, we present the Goal-based Game-tree

Search algorithm (denoted as GB-GTS) developed for

game playing in the complex scenarios and address-

ing the listed challenges. We describe the problems of

simultaneous moves, present our deﬁnition of goals,

and then follow with a description of the algorithm

and how it can be employed in a game-playing agent.

3.1 Domain

The domains supported by the algorithm can be

formalized as a tuple (P , U, A, W , T ), where P

is the set of players, U =

p∈P

is a set of

units/resources capable of performing actions in the

world, each belonging to one of the players. A =

u∈U

is a set of combinations of actions the units can

perform, W is the set of possible world states and

T : W × A → W is the transition function realiz-

ing one move of the game where the game world is

changed via actions of all units and world’s own dy-

namics.

The game proceeds in moves in which each player

assign actions to all the units it controls (forming the

action of the player) and the function T is called with

joint action of all players’ action to change the world

state.

3.2 Simultaneous Moves

There are two options for dealing with simultaneous

moves. The ﬁrst one is to directly work with joint ac-

tions of all players in each move, compute their val-

ues and consider the game matrix (normal form game)

they create. The actions of individual players can then

be chosen based on a game-theoretical equilibrium

(e.g. Nash equilibrium in (Sailer et al., 2007)). The

second option is to ﬁx the order of the players and let

them choose their actions separately in the same way

as in max

, but using the unchanged world state from

the end of the previous move for all of them and with

the actions’ execution delayed until all players have

chosen their actions. This method is called delayed

execution in (Kovarsky and Buro, 2005). In our exper-

iments, we have used the approach with ﬁxed players’

order, because of easier implementation and to focus

the research on usage of backgroung knowledge.

3.3 Goals

For our algorithm we deﬁne a goal as a pair (I

, A

where I

(W , U) is the initiation condition of the goal

ICAART 2009 - International Conference on Agents and Artificial Intelligence

and A

is an algorithm that, depending on its internal

state and the current state of the world, deterministi-

cally outputs the next action that leads to fulﬁlling the

goal.

A goal can be assigned to one unit and it is then

pursued until it is successfully reached or dropped,

because its pursuit is no longer practical. Note, that

we do not specify any dropping or succeeding condi-

tion, as they are implicitly captured in A

algorithm.

We allow the goal to be abandoned only if A

is ﬁn-

ished, and each unit can pursue only one goal at a

time. There are no restriction on complexity of algo-

rithm A

, so this kind of goals can represent any goal

from the taxonomy of goals presented in (van Riems-

dijk et al., 2008) and any kind of architecture (e.g.

BDI, HTN) can be used to describe it.

The goals in GB-GTS serve as building blocks

for more complex strategies that are created by com-

bining different goals for different units and then ex-

plored via search. It is in contrast with the HTN-based

approaches used for guiding the game tree search (see

Section 5), where the whole strategies are encoded us-

ing decompositions from the highest levels of abstrac-

tion to the lower ones.

3.4 Algorithm Description

The main procedure of the algorithm (sketched in Fig-

ure 1 as procedure GBSearch()) recursively computes

the value of a state for each of the players assuming

that all the units will rationally optimize the utility of

the players controlling them. The inputs to the pro-

cedure are the world state for which the value is to

be computed, the depth to which to search from the

world state and the goals the units are currently pur-

suing. The last parameter is empty when the function

is called for the ﬁrst time.

The algorithm is composed of two parts. The ﬁrst

is the simulation of the world changes based on the

world dynamics and the goals that are assigned to

the units, and the second is branching on all possi-

ble goals that a unit can pursue after it is ﬁnished with

its previous goal.

The ﬁrst part - simulation - consists of lines 1 to

15. If all the units have a goal they actively pursue, the

activity in the world is simulated without any need for

branching. The simulation runs in moves and lines 3-

10 describe the simulation of a single move. At ﬁrst,

for each unit an action is generated based on the goal

g assigned to this unit (line 5). If the goal related algo-

rithm A

is ﬁnished, we remove the goal from the map

of goals (lines 6-8) and the unit, that was assigned to

this goals, becomes idle. The generated actions are

then executed and the conﬂicting changes of the world

Input: W ∈ W : current world state, d: search depth,

G[U]: map from units to goals they pursue

Output: an array of values of the world state (one

value for each player)

curW = W1

while all units have goals in G do2

Actions =

foreach goal g in G do4

Actions = Actions ∪ NextAction(A

if A

is ﬁnished then6

remove g from G7

end8

end9

curW = T (curW ,Actions)10

d = d − 111

if d=0 then12

return Evaluate(curW)13

end14

end15

u = GetFirstUnitWithoutGoal(G)16

foreach goal g with satisﬁed I

(curW , u) do17

G[u] = g18

V [g] = GBSearch(curW, d,Copy(G))19

end20

g = argmax

V [g][Owner(u)]21

return V [g]22

Figure 1: GBSearch(W , d, G) - the main procedure of GB-

GTS algorithm.

are resolved in accordance with game rules (line 10).

After this step, one move of the simulation is ﬁnished.

If the simulation has reached the required depth of

search, the resulting state of the world is evaluated

using the evaluation functions of all players (line 13).

The second part of the algorithm - branching -

starts when the simulation reaches the point where

at least one unit has ﬁnished pursuing its goal (lines

16-22). In order to assure the ﬁxed order of players

(see Section 3.2), the next processed unit is chosen

from the idle units based on the ordering of the play-

ers that control the units (line 16). In the run of the

algorithm, all idle units of one player are considered

before moving to the units of the next one. The rest

of the procedure deals with the selected unit. For this

unit, the algorithm sequentially assigns each of the

goals that are applicable for the unit in the current

situation. The applicability is given by the I

con-

dition of the goal. For each applicable goal, it assigns

the goal to the unit and evaluates the value of the as-

signment by recursively calling the whole GBSearch()

procedure (line 19). The current goals are cloned, be-

cause the state of the already started algorithms for

the rest of the units (A

) must be preserved. After

computing the value of each goal assignment, the one

that maximizes the utility of the owner of the unit is

chosen (line 21) and the values of this decision for all

GOAL-BASED ADVERSARIAL SEARCH - Searching Game Trees in Complex Domains using Goal-based Heuristic

players are returned by the procedure.

3.5 Game Playing

The pseudo-code on Figure 1 shows only the compu-

tation of the values of the decisions and does not deal

with how to actually use it to determine player’s ac-

tion in the game. In order to do so, a player needs to

extract a set of goals for its units from the searched

game-tree. Each node in the search procedure execu-

tion tree is associated with a unit – the unit for which

the goals are tried out. During the run of the algo-

rithm, we store the maximizing goal choices from the

top of the search tree representing the ﬁrst move of

the game. The stored goals for each idle unit of the

searching player are the main output of the search.

In general, there are two possibilities how to

use proposed goal-based search algorithm in game-

playing.

The ﬁrst approach lies in starting the algorithm in

each move and with all the units in the simulation set

to idle. The resulting goals are extracted and the ﬁrst

action is generated for each of the goals and that are

the actions played in the game. Such an approach is

better for coping with unexpected events and it should

be beneﬁcial if the background knowledge does not

exactly describe the activities in the game.

In the second approach the player, that uses the al-

gorithm, keeps the current goal for each of the units

it controls. If none of its units is idle, it just uses the

goals to generate actions for its units. Otherwise, the

search algorithm is started with the goals for the non-

idle units controlled by the player pre-set and all the

other units idle. The resulting goals for the searching

player’s units that were idle are used and pursued in

next moves. This approach is much less computation-

ally intensive.

3.6 Opponent Models

The search algorithm introduced in this section is

very suitable for the use of opponent models, that are

proved to be useful in adversarial search in (Carmel

and Markovitch, 1996). There are two kinds of oppo-

nent model present in the algorithm. One is already

an essential part of the max

algorithm. It is the set

of evaluation functions capturing basic preferences of

each opponent.

The other opponent model can be used to reduce

the set of all applicable goals (iterated in Figure 1 on

lines 18-21) to the goals a particular player is likely

to pursue. This can be done by adding player-speciﬁc

constrains to conditions I

deﬁning when the respec-

tive goal is applicable. These constrains can be hand-

coded by an expert or learned from experience; we

call them goal-restricting opponent models.

It can be illustrated on a simple example of the

goal representing loading a commodity to a truck.

The domain restriction I

could be that the truck must

not be full. The additional constrain could be that the

commodity must be produced locally at the location,

because the particular opponent never uses temporary

storage locations for the commodity and always trans-

ports it from the place where it is produced to the

place where it is consumed.

Using a suitable goal-restricting opponent model

can further reduce the size of the space that needs to

be searched by the algorithm.

A similar way of pruning is possible also in ad-

versarial search without goals, but we believe, that

assessing what goals would a player pursue in a sit-

uation is more intuitive and easier to learn than which

basic action (e.g. going right or left on a crossroad) a

player will execute.

4 EXPERIMENTS

In order to practically examine proposed goal-based

(GB) search algorithm we performed several exper-

iments. Firstly, we compare it to exhaustive search

performed by the simultaneous move modiﬁcation of

max

that we call action-based (AB) search and we

assess the ability to reduce the volume of search on

one side and maintain the quality of resulting strate-

gies on the other. Then we analyze scalability of GB

algorithm in more complex scenarios. Note that we

use the worst-case scenario in the experiments. All

units are choosing their goals at the same moment.

This does not happen often if we use the lazy ap-

proach which only assigns actions to units that be-

come idle (see Section 3.5).

4.1 Example Game

The story behind the game we use as a test case for our

algorithm is a humanitarian relief operation in an un-

stable environment, with three players - government,

humanitarian organization, and separatists. Each of

the players controls a number of units with different

capabilities that are placed in the game world repre-

sented by a graph. Any number of units can be lo-

cated in each vertex of the graph and change its posi-

tion to an adjacent vertex in one game move. Some of

the vertices of the graph contain cities, that can take

in commodities the players use to construct buildings

and produce other commodities.

ICAART 2009 - International Conference on Agents and Artificial Intelligence

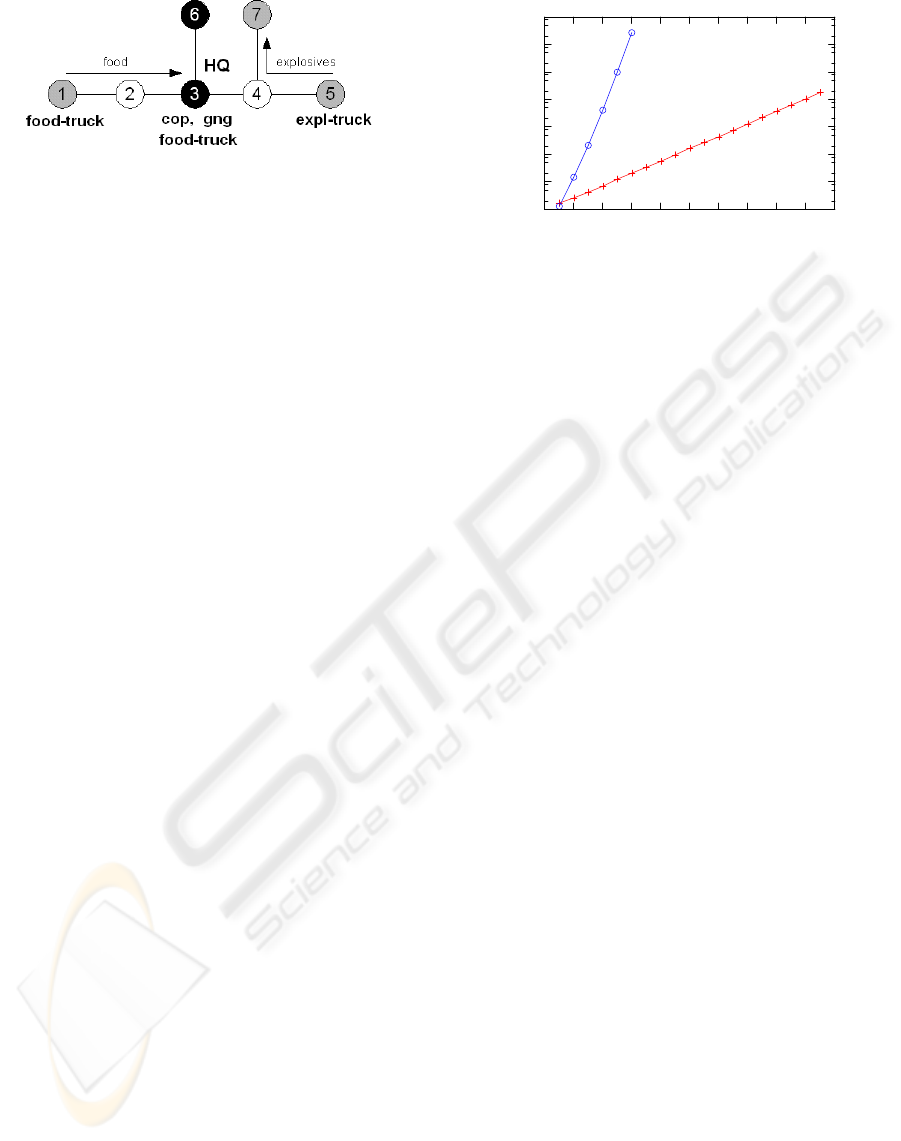
Figure 2: A schema of the simple scenario. Black vertices

represent cities that can be controlled by players, grey ver-

tices represent cities that cannot be controlled, and white

vertices do not contain cities.

The utilities (evaluation functions) representing

the main objectives of the players are generally

weighted sums of components, such as the number

of cities with sufﬁcient food supply, or the number of

cities under the control of government. The govern-

ment control is derived from the state of the infras-

tructure, the difference between the number of units

of individual players in the city and the state of the

control of the city in the previous move.

The goals, used in the algorithm, are generated by

instantiation of ﬁfteen goal types. Each goal type is

represented as a Java class. Only four of the ﬁfteen

classes are unique and the rest nine classes are derived

form four generic classes in a very simple way. The

actions leading towards achieving a goal consist typ-

ically of path-ﬁnding to a speciﬁc vertex, waiting for

a condition to hold, performing a speciﬁc action (e.g.

loading/unloading commodities), or their concatena-

tion. The most complex goal is escorting a truck by

cop that consists of estimating a proper meeting point,

path planing to that point, waiting for the truck, and

accompanying it to its destination.

Simple Scenario: In order to run the classical AB

algorithm on a game of this complexity, the scenario

has to be scaled down to a quite simple problem. We

have created such simpliﬁed scenario as a subset of

our game. It is shown in Figure 2 and the main char-

acteristics are explained here:

• only two cities can be controlled (Vertices 3 and 6)

• a government’s HQ is built in Vertex 3

• two “main” units - police (cop) and gangster (gng)

are placed in Vertex 3

• a truck is transporting explosives from Vertex 5 to

Vertex 7

• another two trucks are transporting food from Ver-

tex 1 to the city with food shortage Vertex 3

There are several possible runs of this scenario.

The police unit has to protect several possible threats.

In order to make government to lose control in Ver-

tex 3, the gangster can either destroy food from a

0 2 4 6 8 10 12 14 16 18 20

Nodes

Search Depth

Figure 3: The search space reduction of the GB algorithm

(pluses) compared to the AB algorithm (circles). An aver-

age number (over all 450 test problems) of the search tree

nodes explored depending on the search depth is shown for

both algorithms in a logarithmic scale.

truck to cause starving resulting in lowering the well-

being and consequent destroying of the HQ (by riots),

or it can steal explosives and build a suicide bomber

that will destroy the HQ without reducing wellbeing

in the city. Finally, it also can try to gain control in

city in Vertex 6 just by outnumbering the police there.

In order to explore all these options, the search depth

necessary is six moves.

Even such a small scenario creates too big a game

tree for the AB algorithm. Five units with around four

applicable actions each (depending on the state of

the world) considered in six consequent moves makes

)

≈ 10

world states to examine. Hence, we fur-

ther simplify it for this algorithm. Only the actions of

two units (cop and gng) are actually explored in the

AB search and the actions of the trucks are consid-

ered to be a part of the environment (i.e. the trucks

are scripted to act rationally in this scenario). Note

that GB algorithm does not need this simpliﬁcation

and actions of all units are explored in GB algorithm.

4.2 Search Reduction

Using this simpliﬁed scenario we ﬁrstly analyze how

the main objective of the algorithm – search space

reduction – is satisﬁed.

We run the GB and AB algorithms on a ﬁxed set of

450 problems – world states samples extracted from

30 different traces of the game and we increased the

look-ahead for both algorithm. As we can see in Fig-

ure 3, the experimental results fulﬁlled our expec-

tations of substantial reduction of the search space.

The number of nodes explored increases exponen-

tially with the depth of the search. However, the base

of the exponential is much lower for the GB algo-

rithm. The size of the AB tree for six moves look-

ahead is over 27 million, while GB search with the

same look-ahead explores only 208 nodes and even

GOAL-BASED ADVERSARIAL SEARCH - Searching Game Trees in Complex Domains using Goal-based Heuristic

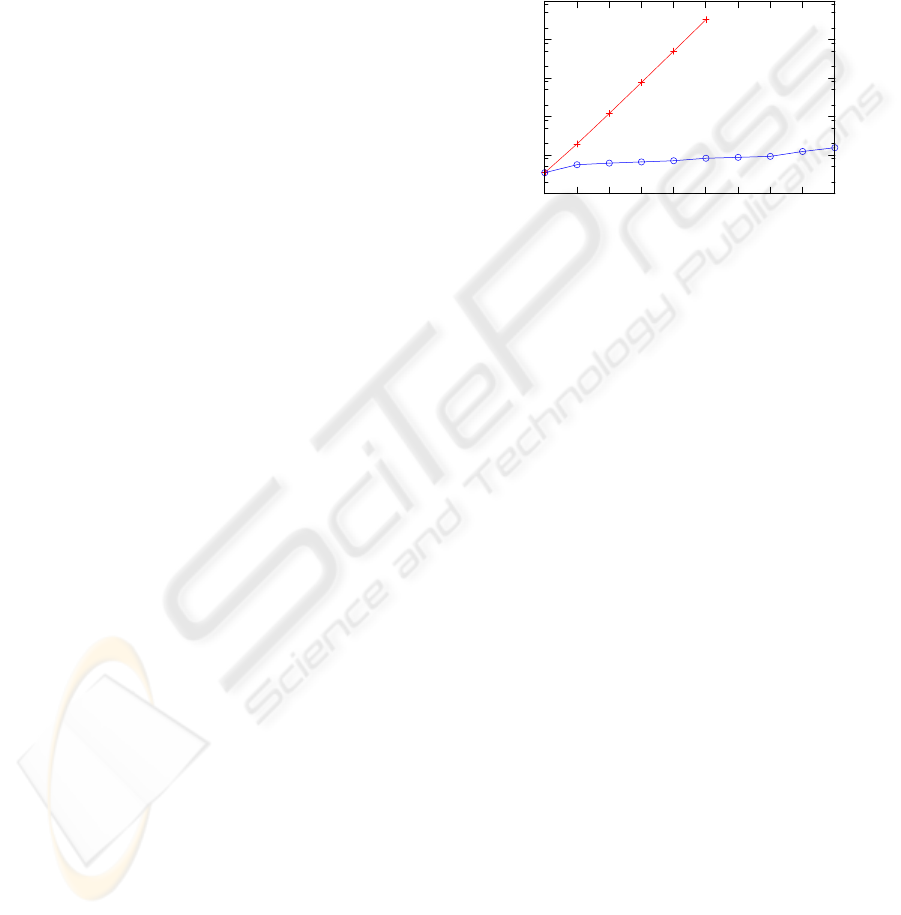
for look-ahead of nineteen, the size of the tree was in

average less than 2×10

. These numbers indicate that

using heuristic background knowledge can reduce the

time needed to choose an action in the game from tens

of minutes to a fraction of second.

Our implementations of each of the algorithms

processed approximately twenty ﬁve thousands nodes

per second on our testing hardware without any opti-

mization techniques. However, according to (Billings

et al., 2004), game trees with million nodes can be

searched in real-time (about one second) when such

an optimization is applied and when efﬁcient data

structures are used.

4.3 Loss of Accuracy

With such substantial reduction of the set of possi-

ble courses of action explored in the game, some loss

of quality of game-playing can be expected. Using

the simpliﬁed scenario, we compared the actions re-

sulting from the AB and the ﬁrst action generated by

the goal resulting from the GB algorithm. The ac-

tion differed in 47% of cases. However a different

action does not necessarily mean that the GB search

has found a sub-optimal move. Two different actions

often have the same value in AB search. Because of

the possibly different order in which actions are con-

sidered, the GB algorithm can output an action which

is different from the AB output yet still has the same

optimal value. The values of actions referred to in the

next paragraph all come from the AB algorithm.

The value of the action resulting from GB algo-

rithm was in 88.1% of cases exactly the same as the

“optimal” value resulting from AB algorithm. If the

action chosen by GB algorithm was different, it was

still often close to the optimal value. We were mea-

suring the difference between the values of GB and

optimal actions, relative to the difference between the

maximal and the minimal value resulting from the

searching players decisions in the ﬁrst move in the

AB search. The mean relative loss of the GB algo-

rithm was 9.4% of the range. In some cases, the GB

algorithm has chosen the action with minimal value,

but it was only in situations, where the absolute dif-

ference between the utilities of the options was small.

4.4 Scalability

Previous sections show that the GB algorithm can be

much faster than and almost as accurate as the AB al-

gorithm with suitable goals. We continue with assess-

ing the limits on the complexity of the scenario where

GB algorithm is still usable. There are several possi-

ble expansions of the simple scenario. We explore the

most relevant factor – number of units – separately

and then we apply the GB algorithm on a bigger sce-

nario. In all experiments, we ran the GB algorithm

in the initial position of the extended simple scenario

and we measured the size of the searched part of the

game tree.

4.4.1 Adding Units

1 2 3 4 5 6 7 8 9 10

Nodes

Units Added

Figure 4: Increase of the size of the searched tree when

adding one to ten police units (pluses) and explosives trucks

(circles) to the simple scenario with 6 move look-ahead.

The increase of the size of the searched tree natu-

rally depends on the average number of goals applica-

ble for a unit when it becomes idle and the lengths of

the plans that lead to their fulﬁllment. The explosives

truck has usually only a couple of applicable goals. If

it is empty, the goal is to load in one of the few cities

where explosives are produced and if it is full, the goal

is unloading somewhere where explosives can be con-

sumed. On the other hand, a police unit has a lot of

possible goals. It can protect any transport from being

robbed and it can try to outnumber the separatists in

any city. We were adding these two unit types to the

simple scenario and computed size of the search tree

with ﬁxed six moves look-ahead.

When adding one to ten explosives trucks to the

simple scenario, each of them has always only one

goal to pursue at any moment. Due to our GB algo-

rithm deﬁnition, where goals for each unit are evalu-

ated in different search tree node, even adding a unit

with only one possible goal increases the number of

evaluated nodes slightly. In Figure 4 are the results

for this experiment depicted as circles. The number

of the evaluated nodes increases only linearly with in-

creasing the number of the trucks.

Adding further police units with four goals each

to the simple scenario increased the tree size expo-

nentially. The results for this experiment are shown

in Figure 4 as pluses.

ICAART 2009 - International Conference on Agents and Artificial Intelligence

4.4.2 Complex Scenario

In order to test usability of GB search on more re-

alistic setting, we implemented a larger scenario of

our game. We used a graph with 2574 vertices and

two sets of units. The ﬁrst was composed of nine

units, including two police units with up to four pos-

sible goals in one moment, two gangster units with up

to four possible goals, an engineer with three goals,

stone truck with up to two goals and three trucks with

only one commodity source and one meaningful des-

tination resulting to one goal at any moment. The sec-

ond included seven units – one police, one gangster

unit and the same amount of units of the other types.

The lengths of the plans to reach these goals is ap-

proximately seven basic actions. There are ﬁve cities,

where the game is played.

A mayor difference of this scenario to the simple

scenario is, besides the added units, a much bigger

game graph and hence higher lengths of the routes

between cities. As a result, all the plans of the units

that need to arrive to a city and perform some actions

there are proportionally prolonged. This is not a prob-

lem for the GB algorithm, because the move actions

along the route are just simulated in the simulation

phase and do not cause any extra branching.

In a simple experiment to prove this, we changed

the time scale of the simulation, so that all the actions

were split to two sub-actions performing together the

same change of the game world. After this modiﬁca-

tion, GB algorithm explored exactly the same num-

ber of nodes and the time needed for the computation

increased linearly, corresponding to more simulation

steps needed.

10 11 12 13 14 15 16 17 18

Nodes

Search Depth

Figure 5: Size of the trees searched by GB algorithm in the

complex scenario with 7 (pluses) and 9 (circles) units.

If we assume, that the optimized version of the

algorithm can compute one million nodes in a rea-

sonable time, than the look-ahead we can use in the

complex scenario is 10 in the nine units case and 18

in the seven units case. Both values are higher than

the average length of a plan of a unit so the algorithm

plays meaningfully. If we wanted to apply the AB al-

gorithm to the seven unit case with look-ahead eigh-

teen, considering only four possible move directions

and waiting for each unit, it would mean searching

through approximately 4

≈ 10

nodes of the game

tree, which is nowadays clearly impossible.

5 RELATED WORK

The idea to use domain knowledge in order to re-

duce the portion of the game tree that is searched dur-

ing the play has already appeared in literature. The

best-known example is probably (Smith et al., 1998),

where authors used HTN formalism to deﬁne the set

of runs of the game, that are consistent with some pre-

deﬁned hand-coded strategies. During game playing,

they search only that part of the game tree.

A plan library represented as HTN is used to play

GO in (Willmott et al., 2001). The searching player

simulates HTN planning for both the players, without

considering what is the other one trying to achieve. If

one player achieves its goal, the opponent backtracks

(the shared state of the world is returned to a previous

state) and tries an other decomposition.

Both these works use quite detailed descriptions

of the whole space of the meaningful strategies in

HTN. Another approach for reducing the portion of

the tree that is searched for scenarios with multiple

units is introduced in (Mock, 2002). The authors

show successful experiments with searching just for

one unit at a time, while simulating the movements of

the other units using rule-based heuristic.

An alternative to using the game-tree search is

summarized in (Stilman et al., 2007). They solve

large scale problems with multiple units using, be-

sides other methods, generation of the meaningful

sequences of unit actions pruned according to vari-

ous criteria. One of them is whether they can be in-

tercepted (rendered useless or counterproductive) by

traces of the opponent’s units.

6 CONCLUSIONS

We proposed a novel approach to introducing

background knowledge heuristic to multi-player

simultaneous-move adversarial search. The approach

is particularly useful in domains where long se-

quences of actions lead to signiﬁcant changes in the

world state, each of the units (or other resources) can

only pursue a few goals at any time and the decompo-

sition of a each goal to low level actions is uniquely

GOAL-BASED ADVERSARIAL SEARCH - Searching Game Trees in Complex Domains using Goal-based Heuristic

deﬁned (e.g. using the shortest path to move between

locations).

We have compared the performance of the algo-

rithm to a slightly modiﬁed exhaustive max

search,

showing that despite examining only a small fraction

of the game tree (less than 0.001% for the look-ahead

of six game moves), the goal-based search is still

able to ﬁnd an optimal solution in 88.1% cases; fur-

thermore, even the suboptimal solutions produced are

very close to the optimum. This results have been ob-

tained with the background knowledge designed be-

fore implementing and evaluating the algorithm and

without further optimization to prevent over-ﬁtting.

Furthermore, we have tested the scalability of

the algorithm to larger scenarios where the modiﬁed

max

search cannot be applied. We have conﬁrmed

that although the algorithm cannot overcome the ex-

ponential growth, this growth controllable by reduc-

ing the number of different goals a unit can pursue

and by making the action sequences generated by

goals longer. Simulations on a real-world scenario

modelled as an multi-player asymmetric game proved

the approach viable, though further optimizations

and more improved background knowledge would be

needed for the algorithm to discover complex strate-

gies.

An important feature of the proposed approach

is its compatibility with all existing extensions of

general-sum game tree search based on modiﬁed

value back-up procedure and other optimizations. It

is also insensitive to the granularity of space and time

with which a game is modelled as long as the structure

of the goals remains the same and their decomposition

into low-level actions is scaled correspondingly.

In future research, we aim to implement additional

technical improvements in order to make the goal-

based search applicable to even larger problems. In

addition, we would like to address the problem of

the automatic extraction of goal-based background

knowledge from game histories. First, we will learn

goal initiation conditions for individual players and

use them for additional search space pruning. Sec-

ond, we will address a more challenging problem of

learning the goal decomposition algorithms.

ACKNOWLEDGEMENTS

Effort sponsored by the Air Force Ofﬁce of

Scientiﬁc Research, USAF, under grant number

FA8655-07-1-3083 and by the Research Programme

No.MSM6840770038 by the Ministry of Education of

the Czech Republic. The U.S. Government is autho-

rized to reproduce and distribute reprints for Govern-

ment purpose notwithstanding any copyright notation

thereon.

REFERENCES

Billings, D., Davidson, A., Schauenberg, T., Burch, N.,

Bowling, M., Holte, R. C., Schaeffer, J., and Szafron,

D. (2004). Game-tree search with adaptation in

stochastic imperfect-information games. In van den

Herik, H. J., Bjrnsson, Y., and Netanyahu, N. S., edi-

tors, Computers and Games, volume 3846 of Lecture

Notes in Computer Science, pages 21–34. Springer.

Carmel, D. and Markovitch, S. (1996). Learning and us-

ing opponent models in adversary search. Technical

Report CIS9609, Technion.

Kovarsky, A. and Buro, M. (2005). Heuristic search applied

to abstract combat games. In Canadian Conference on

AI, pages 66–78.

Luckhardt, C. and K.B.Irani (1986). An algorithmic solu-

tion of n-person games. In Proc. of the National Con-

ference on Artiﬁcial Intelligence (AAAI-86), Philadel-

phia, Pa., August, pages 158–162.

Mock, K. J. (2002). Hierarchical heuristic search techniques

for empire-based games. In IC-AI, pages 643–648.

Sailer, F., Buro, M., and Lanctot, M. (2007). Adversarial

planning through strategy simulation. In IEEE Sym-

posium on Computational Intelligence and Games

(CIG), pages 80–87, Honolulu.

Schaeffer, J. (1989). The history heuristic and alpha-

beta search enhancements in practice. IEEE Trans-

actions on Pattern Analysis and Machine Intelligence,

11(11):1203–1212.

Smith, S. J. J., Nau, D. S., and Throop, T. A. (1998). Com-

puter bridge - a big win for AI planning. AI Magazine,

19(2):93–106.

Stilman, B., Yakhnis, V., and Umanskiy, O. (2007). Ad-

versarial Reasoning: Computational Approaches to

Reading the Opponent’s Mind, chapter 3.3. Strategies

in Large Scale Problems, pages 251–285. Chapman

& Hall/CRC.

van Riemsdijk, M. B., Dastani, M., and Winikoff, M.

(2008). Goals in agent systems: A unifying frame-

work. In Padgham, Parkes, Mller, and Parsons, ed-

itors, Proc. of 7th Int. Conf. on Autonomous Agents

and Multiagent Systems (AAMAS 2008), volume Es-

toril, Portugal, pages 713–720.

Willmott, S., Richardson, J., Bundy, A., and Levine, J.

(2001). Applying adversarial planning techniques to

Go. Theoretical Computer Science, 252(1–2):45–82.

ICAART 2009 - International Conference on Agents and Artificial Intelligence