DOCUMENT RELATION ANALYSIS BASED ON

COMPRESSIBILITY VECTOR

Nuo Zhang, Daisuke Matsuzaki, Toshinori Watanabe and Hisashi Koga

Graduate School of Information Systems, The University of Electro-Communications

1-5-1, Chofugaoka, Chofu-shi, Tokyo, Japan

Keywords:

Document analysis, PRDC, Topic extraction, Relation analysis, Clustering, Data compression.

Abstract:

Nowadays, there are a great deal of e-documents can be easily accessed. It will be beneﬁcial if a method can

evaluate documents and abstract signiﬁcant content. Similarity analysis and topic extraction are widely used

as document relation analysis techniques. Most of the methods are based on dictionary-base morphological

analysis. They cannot meet the requirement when the Internet grows fast and new terms appear but dictionary

cannot be automatically updated fast enough. In this study, we propose a novel document relation analysis

(topic extraction) method based on a compressibility vector. Our proposal does not require morphological

analysis, and it can automatically evaluate input documents. We will examine the proposal with using model

document and Reuters-21578 dataset, for relation analysis and topic extraction. The effectiveness of the

proposed method will be shown in simulations.

1 INTRODUCTION

When handling enormous number of documents, it is

convenient to appropriately know topics or keywords

in advance. Since most documents have various opin-

ions and intention, a document may have multiple

topics. When we consider multiple topics in docu-

ments (such as documents on the Internet), there is

a large number of overlapped topics. In a library,

the shelves are lined up with different topics. Obvi-

ously, it is impossible to put one book with more than

one topic into different shelves. On the Internet, we

use hyperlink which can solve the problem above for

Web pages. Many portal sites provide directory type

services, which are still under manual operating for

the classiﬁcation and arrangement of the web pages.

However, as the number of web pages is getting in-

creased, the work of classiﬁcation by human being be-

comes heavy. Therefore, an automatic method to doc-

ument classiﬁcation with multiple topics is required

(Saito, 2005).

Morphological analysis is a fundamental tech-

nique widely used for analyzing documents. In mor-

phological analysis, the knowledge of grammar of the

language and the dictionary are used as information

sources, and the sentence written by the natural lan-

guage is divided into a series of the morpheme. This

is an effective technique in information retrieval, text

mining and clustering for the large-scale document.

Since this method uses dictionary which is built in

advance, it results in distortion for the Internet, where

new terms are produced fast. In this case, the new

terms what are not registered in the dictionary obvi-

ously cannot be processed, which results in fuzziness

in the processing result.

On the other hand, we developed a method to uni-

formly analyze sound, image and text data without

morphological analysis. We named this method as

PRDC (Pattern Representation Scheme Using Data

Compression) (Toshinori Watanabe and Sugihara,

2002), which represents the feature of data as com-

pressibility vector. It measures the distance among the

vectors. We have applied it to analyze multi-media

data and some effective results were obtained.

In this paper, we analyze the document relation

under PRDC framework (Toshinori Watanabe and

Sugihara, 2002) and extract topics. We propose a

method which focuses on the compressibility of the

documents without carrying out natural language pro-

cessing. Some model documents will be created to

verify the proposed method. The real document is

also used in the simulation. Simulation results will

255

Zhang N., Matsuzaki D., Watanabe T. and Koga H. (2009).

DOCUMENT RELATION ANALYSIS BASED ON COMPRESSIBILITY VECTOR.

In Proceedings of the International Conference on Agents and Artiﬁcial Intelligence, pages 255-260

DOI: 10.5220/0001660202550260

 SciTePress

show that the proposed method can help us to under-

stand complexrelationship among documentswithout

using morphological analysis.

2 RELATION ANALYSIS AND

TOPIC EXTRACTION WITH

DATA COMPRESSION

2.1 Representation of Data Feature

using PRDC

In this paper, data compression is used for represen-

tation of overlapped topics. In general, a model of in-

put information source is used for encoding the input

string in data compression. Moreover, a compression

dictionary is used as the model. The compression dic-

tionary is automatically produced when compressing

input data, ex. Lempel-Ziv (LZ) compression (Tim-

othy C. Bell, 1990), (J. Ziv, 1978). In the same way,

PRDC constructs a compression dictionary by encod-

ing input data forms. It makes a compressibility space

from the compression dictionary to project new in-

put data into it. Therefore, we can get the feature of

data represented by a compressibility vector. Finally,

PRDC classiﬁes data by analyzing these compress-

ibility vectors.

2.2 Approach of Document Relation

Analysis

In this paper, we propose a document analysis ap-

proach based on PRDC.

Preprocessing. In the preprocessing procedure, we

unite the code characters, remove the white spaces,

newlines, tabs, and all non-alphabetical characters.

Clustering Similarity Document by PRDC. Sub-

sequently, PRDC is used as followsfor relation analy-

sis of similar documents, which have overlapped top-

ics. Compression dictionaries are obtained by com-

pressing input documentswith Lempel-Ziv(LZ) com-

pression. These dictionaries constitute a compress-

ibility space. Compressibility vector table is made by

projecting the input document into the compressibil-

ity space. Let N

be the input document. By com-

pressing the input document, a compression dictio-

nary is obtained, which is expressed as D

. Com-

pressing document N

by D

, we get compression

ratio C

. Where, L

is the size of the in-

put stream N

, K

is the size of the output stream.

Compressing with all of the dictionaries, we obtain

a compression ratio vector for each input document.

In the compressibility vector table, the columns show

the document data N

, the rows show the compression

dictionary D

formed by the same document, and the

elements show the compression ratio C

[%]. The

similar text in different document can be extracted by

clustering compression ratio vector.

Relation Analysis of Documents. There are com-

mon topics in the documents which belong to each

cluster obtained after using PRDC. Here, we extract

the common topics. A topic in a certain document is

composed of the repetition of some speciﬁc phrases

or words appeared more than once. If these phrases

or words can be found, it is possible to understand the

content of the common topics in a document. PRDC

is used to discover the speciﬁc phrase and word that

belong to common topic. PRDC is used to ﬁrst com-

press the documents in the same cluster respectively,

and then compose compressibility space of the gen-

erated compression dictionary. Next, all of the docu-

ments in a cluster are divided into fragments of length

L characters or words, and all fragments are mapped

to the compressibility space.

From the study of the compressibility of each frag-

ment, a speciﬁc phrase or word can be discovered.

Because that fragments compressed into the same

level by any compression dictionary of any document

appears in common in the cluster. In other words,

the fragment plotted in the diagonal of the compress-

ibility space can be considered as the common topic

between two documents. On the opposite, fragments

which cannot be compressed by any compression dic-

tionary, are plotted far from the origin in the com-

pressibility space. Such fragment is considered as

an ”unknown” fragment in each cluster of the doc-

uments. Then, the relation table is made of extracting

common fragments. By analyzing the fragments in

the table, overlapped topics between documents can

be conﬁrmed.

Presentation of Relation Table. The relation table

is made of extracting common fragments. In case of

the relation is shown for three document A, B, and

C. The extracted fragments are listed in the ﬁrst row

of the table. Which document do the fragments ap-

pear in are displayed by ’O’ or ’X’ from the second

row. Fragment a and b of the second column in the ta-

ble show a common fragment of document A, B and

C. Fragment c and d of the third column in the table

are the common fragment only for document A and

B, etc. And the third and fourth columns are simi-

lar. Moreover, the 6th, 7th and 8th columns show the

ICAART 2009 - International Conference on Agents and Artificial Intelligence

256

peculiar fragments for document A, B, and C respec-

tively. By analyzing the fragments in the table, over-

lapped topics between documents can be conﬁrmed.

The size of the table may increase rapidly when there

are a lot of numbers of documents. In the following,

the number of documents to be analyzed is assumed

to be three at a time.

2.3 Approach of Topic Extraction

To extend the method described previously and auto-

matically extract topics, we compose a long document

by concatenating all incoming documents at ﬁrst.

Then the long document is separated to many frag-

ments with length of L words or characters. PRDC is

employed to classify the fragments to many clusters.

Each centroid fragment is considered as a representa-

tion of the cluster which it belongs to. Moreover, the

words in the centroid fragment are extracted topics.

3 SIMULATION RESULTS AND

ANALYSIS

For a real document, the topics can be different

according to a reader’s understanding and purpose.

Therefore, it is difﬁcult to obtain an objective extrac-

tion of the topic. Which also makes it difﬁcult to ver-

ify the proposed method by using real documents. In-

stead of using a real document, we artiﬁcially make a

document (model document) ﬁrst, and use it to verify

the method at the principle level. Then, we test the

proposed method using real document. The quantita-

tive experiments are carried out to compare our pro-

posed method with SVD (Singular Value Decomposi-

tion) and ICA (Independent Component analysis). In

the following, we will explain how to make the model

document. In simulation 1, the distribution of a com-

mon fragment is examined with consideration of the

extraction method.

3.1 Generation of Model Document

The topic in a document consists of the repetition of

a phrase or word (basic phrase). We make the basic

phrase, and change the number of the repetition ar-

bitrarily. After which, we insert some words among

the basic phrase. These words (noise character) are

not included in the basic phrase vocabulary. That is

achieved by allocating a lot of characters in advance.

In the simulation, the noise character was extracted

from the collection of 7000 characters. Each charac-

ter is selected randomly, and is buried between ba-

sic phrases. By changing the topic and the number

of repetition, we can make any model document and

different overlaps between documents. Therefore,

by applying the proposed relation analysis method to

the model documents, the properties of the proposed

method can be found. Which provides the base anal-

ysis the relation among real documents.

3.2 Simulation 1

Here, the model document with a common basic

phrase is generated. We will show how the fragment

included in the basic phrase is distributed in the com-

pressibility space.

Data. According to the generation method, model

document A, B and C with a common topic are made,

shown in Fig. 1. The number of noise characters is

ﬁxed to 1000 together in all of document A, B and C.

Two types of basic phrase are made and each of which

appears ten times respectively.

Distribution of Common Fragment. The distribu-

tion of all fragments of model document A, B and

C is studied. First, the model document is divided

to the fragment of L characters respectively. To pre-

vent punctuating among basic phrase in the fragment,

we assume that L = 10. All fragments are mapped to

the compressibility space which is composed from the

dictionary of compression of A, B and C. We focus on

model document A. To study what kind of relation the

fragments of A have with document B and C, they are

mapped onto the plane of B-C (Fig. 2).

Here (b, c) = (100, 100) is a fragment with the

noise character that is neither compressed by com-

pression dictionary B nor C. The noise character can

be considered as an unknown fragment. It is plotted

as a distance from the origin. Moreover, the fragment

included in the basic phrase is plotted on the diagonal,

and the distance to the origin is shorter when the basic

phrase becomes longer.

Figure 1: Model document topics of simulation 1.

DOCUMENT RELATION ANALYSIS BASED ON COMPRESSIBILITY VECTOR

257

Figure 2: Face B-C.

3.3 Simulation 2 (Relation Analysis

with Model Documents)

Removal of Stop Words. In document A, B and C

of simulation 1, a lot of noise characters were used,

and each character except two common words “cat”

and “monkey” appears only once. Therefore, frag-

ments that can neither be compressed by compres-

sion dictionary X nor Y were plotted in (X,Y) =

(100, 100). However, stop words appear in actual

documents with different content are similar. A stop

word is a literarily meaningless word for distinguish-

ing documents, such as “a”, “the”, “this” and “when”

etc., in English.

If a fragment contains stop words that are regis-

tered in compression dictionary X or Y, it moves to

the direction of the origin. That is due to the inﬂu-

ence of the stop words. This result causes a problem

when analyzing relation of documents.

We can often ﬁnd stop words in any document.

From our investigation,the compressionratio is 70-90

% between documents with different contents. There-

fore, it is expected that: to add dictionaries generated

from various documents, and concentrate the frag-

ments (with stop words) close to the origin. Accord-

ingly, the common topic can be classiﬁed. We imple-

ment this by using the generated documents A-J. The

results are shown in table 1 and table 2.

Data for Simulation. We made model document A,

B and C with the relation, which is shown in Fig.

3. The variety of the noise character is decreased

from 7000 types to 20 types to cause the inﬂuence

between documents. From the 20 types, we randomly

extracted model document A, B and C and 1000 char-

acters as noise character. Therefore, the documents

share the same stop words. Seven of basic phrase are

made appeared 10 times each.

Moreover, besides A, B and C, we extract 1000

noise character from the 20 types to generate another

7 model document D, E, F, G, H, I,and J without basic

phrase.

Figure 3: Model document topics of Simulation 2.

Figure 4: Dendrogram.

Clustering. The generated model documents are

compressed respectively, and the compressibility

space is composed of the generated compression dic-

tionary. After mapping data onto the compressibil-

ity space, the clustering result of column vector from

group average method is obtained. We can see that

model document A, B and C that have the relation

were extracted as the same cluster, and separated from

others. That is, basic phrases in A, B and C show the

compressibility as common topics.

Document Relation Analysis. Next, the extracted

relation between model document A, B and C is an-

alyzed. First, the model documents are divided into

fragments of L characters (L = 10) respectivelyas that

in simulation 1. And, these are mapped to the com-

pressibility space which is composed of compression

dictionary A, B and C.

Here, we focus on document A and study its rela-

tion between fragments in model document B and C.

For that, the fragments of document A are mapped on

the B-C plane (Fig. 5).

Table 1 shows that fragments that do not include

”monkey”, which is a common topic of model doc-

ument A, B and C, are extracted. A similar phe-

nomenon is also found with model document B and

C. This means that the basic phrase of common topic

and fragment with only noise characters are extracted.

That is due to the existence of stop words. We remove

the stop word fragment. Table 2 shows the extracted

topics.

ICAART 2009 - International Conference on Agents and Artificial Intelligence

258

Relation Table of Documents. In the same way, re-

lation table of model document B and C with removed

stop words, is shown in table 3. As the common topic

between A, B and C, fragmentsincluding basic phrase

“monkey” are extracted. Fragments with “eagle” in B

and C, and “cat” in A and C are extracted. Moreover,

each peculiar fragment “dog”, “owl”, and “hawk” in

model document A, B and C respectively, can also

be extracted. Therefore, the relation analysis between

documents can be achieved even in model documents

that contain stop words, by using PRDC.

Figure 5: Face B-C.

3.4 Simulation 3 (Comparison of

PRDC, ICA and SVD)

Singular Value Decomposition (SVD) is a classical

linear algebra method. It is widely used in signal pro-

cessing and information retrieval. Independent Com-

ponent Analysis (ICA) is a signal processing method

and applied to information retrieval recently. In this

study, we applied SVD and ICA to topic extraction

and compared them with our proposed method.

In the preprocessing procedure, the white spaces,

newlines, and tabs are replaced by a single space.

Non-alphabetical characters are also replaced by a

single space. Upper case characters are all converted

to lower case. And all stop words are removed based

on the standard van Rijsbergen stop word list (Rijs-

bergen, 2008). After that, each word is stemmed by

using Porter’s Stemmer (Porter, 2008). After the pre-

processing, a long text stream is composed by con-

catenating all input documents. Then the long doc-

ument is separated to a number of fragments with

length of L words. Each fragment is represented by a

vector with dimension n, where n is the number of the

words appeared in the text stream. A feature matrix

is then obtained for representation of all fragments.

SVD or ICA are applied the feature matrix to extract

topic vector.

For PRDC, the white spaces, newlines, tabs, non-

alphabetical characters and upper case characters

were processed in the same way with SVD and ICA,

in the preprocessing procedure. And all stop words

Table 1: Common fragments.

Table 2: Common fragments (after removing stop words).

are removed based on the method described in Sim-

ulation 2. Also, a long text stream is composed by

concatenating all input documents. Then the long

document is separated to a number of fragments with

length of L words. Then, PRDC is used to classify

the fragments to a number of clusters. Each centroid

fragment is considered as a representation of the clus-

ter which it belongs to. Moreover, the words in the

centroid fragment are extracted topics.

A classical measure called jaccard (Eq. 1) is uti-

lized to evaluate the topic extraction results. In Eq.

1, α and β are word sets, ∪, and ∩ are the number of

union and intersection between α and β. In this simu-

lation, the top 20 topics are extracted from each set by

using TF-IDF. Because a subset of each topic is used,

we run simulation 10 times and compute the average

for evaluation.

Jaccard(α, β) =

∩(α, β)

∪(α, β)

(1)

A subset of Reuters-21578 is utilized in this simu-

lation. This dataset consists of 21578 news appeared

on the Reuters newswire in 1987 (Ltd., 2008). The

documents were assembled and indexed with cate-

gories by personnel from Reuters Ltd. and Carnegie

Group, Inc. Reuters-21578 is currently the most

widely used test collection in information retrieval,

machine learning, and other corpus-based research.

Since the dataset contains some noise, such as re-

Table 3: Part of document relation table.

DOCUMENT RELATION ANALYSIS BASED ON COMPRESSIBILITY VECTOR

259

peated documents, unlabeled documents, and empty

documents, we choose a subset of 10 relatively large

groups (acq, coffee, crude, earn, interest, money-fx,

money-supply, ship, sugar, and trade) in our experi-

ments. For each of the articles in the 10 categories

that will be used, only the text bodies are extracted.

3.4.1 Simulation with Large-scale Dataset

In this simulation, we used 100 documents from the

set of each topic, and the total number of used doc-

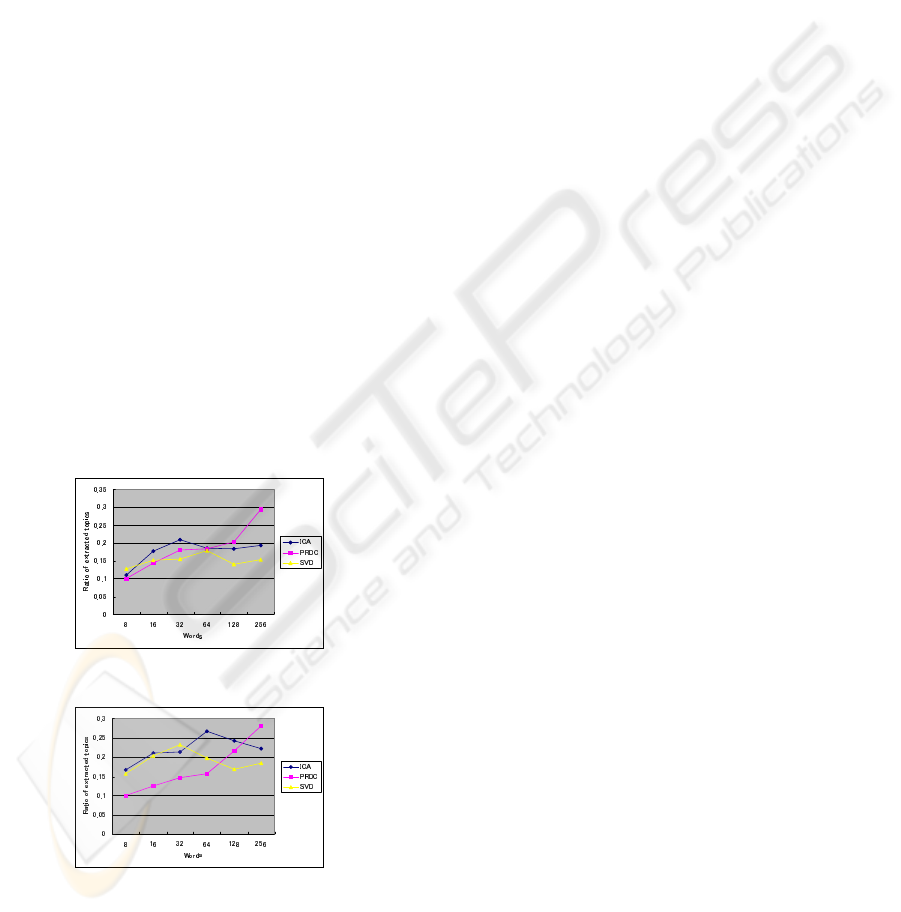
uments is 1000. The results are shown in Fig. 6. L

is set to be 8, 16, 32, 64,128, and 256 to test the per-

formance in different situation. ICA shows better per-

formance than that of SVD and PRDC methods when

L < 64, and SVD and PRDC are not much worse than

ICA method. When L becomes larger, PRDC shows

better performance than that of SVD and ICA meth-

ods. ICA and SVD show the best results when L = 32

or L = 64. According to L becoming large, the perfor-

mance never becomes better. In the contrast, the per-

formance of PRDC becomes better when L get larger.

The proposed method showed better performance

comparing with SVD and ICA methods when L > 64.

And the proposed method provides similar perfor-

mance with the other methods when L < 64. PRDC

method does not need to work with a stop list. It

shows good performance with a set of chose doc-

uments, which means preventing from complicated

computation of dimension reduce.

Figure 6: Ratio of extracted topics for large scale data.

Figure 7: Ratio of extracted topics for small scale data.

3.4.2 Simulation with Small-scale Dataset

In this simulation, we used 10 documents from the

set of each topic, and the total number of used docu-

ments is 100. The results are shown in Fig. 6. L is set

to be 8, 16, 32, 64,128, and 256. The performance of

ICA is similar to SVD, and it is better than that of the

proposed method when L < 128. When L becomes

larger, PRDC shows better performance than that of

SVD and ICA methods. SVD and ICA show the best

results when L = 32 or L = 64. According to L be-

coming large, the performance never becomes better.

In the contrast, the performance of PRDC becomes

better when L get larger.

The proposed method showed better performance

comparing with SVD and ICA methods when L >

128. As the same reason, the proposed method shows

good performance with a set of chose documents,

which means preventing from complicated computa-

tion of dimension reduce.

4 CONCLUSIONS

In this paper, we proposed a method for relation anal-

ysis and topic extraction of documents by using the

compressibility of data. We considered overlapped

topics among documents. The results by using model

document and actual document showed the effective-

ness of the proposed method. The proposed method

does not need natural language processing technique.

In the simulations, we achieved the goal of generating

the model documents and to remove the stop word as

well.

REFERENCES

J. Ziv, A. L. (Sept. 1978). Compression of indi-

vidual sequence via variable-rate coding. IEEE

Trans.Inf.Theory, IT-24(5):530–536.

Ltd., R. (Mar 2008). Reuters-21578 text categoriza-

tion test collection. Reuters-21578 dataset from

http://www.daviddlewis.com/resources/testcollections/

reuters21578/.

Porter, M. (Mar 2008). The porter stemming algorithm.

http://tartarus.org/ martin/PorterStemmer/.

Rijsbergen, V. (Mar 2008). stop word

list. http://ftp.dcs.glasgow.ac.uk/idom/ir-

resources/linguistic-utils/stop-words.

Saito, K. (Vol. 3, No. 3, pp. 15-18, 2005). Multiple topic

detection by parametric mixture models (pmm) auto-

matic web page categorization for browsing. In NTT

Technical Review.

Timothy C. Bell, John G. Cleary, I. H. W. (1990). Text

compression. Prentice-Hall.

Toshinori Watanabe, K. S. and Sugihara, H. (May. 2002).

A new pattern representation scheme using data com-

pression. IEEE TransPAMI, 24(5):579–590.

ICAART 2009 - International Conference on Agents and Artificial Intelligence

260