ATAZAPPER: GENERATING INCOMPLETE DATASETS

Yingying Wen, Kevin B. Korb

Clayton School of Information Technology, Monash University, 3800, VIC, Australia

Ann E. Nicholson

Clayton School of Information Technology, Monash University, 3800, VIC, Australia

Keywords:

Machine learning, Incomplete data, Data generation, Data analysis, Missing data, Data mining, Machine

learning evaluation.

Abstract:

Evaluating the relative performance of machine learners on incomplete data is important because one common

problem with real data is that the data is often incomplete, which means that some values in the data are not

present. DataZapper is a tool for uncreating data: given a dataset containing joint samples over variables,

DataZapper will make a speciﬁed percentage of observed values disappear, replaced by an indication that

the measurement failed. Since the causal mechanisms of measurement that result in failed measurements may

depend in arbitrary ways upon the system under study, it is important to be able to produce incomplete data sets

which allow for such arbitrary dependencies. DataZapper is the only tool that allows any kind of dependence,

and any degree of dependence, in its generation of missing data. We illustrate its use in a machine learning

experiment and offer it to the data mining and machine learning communities.

1 INTRODUCTION

Machine learning (ML) research aims at ﬁnding the

most effective algorithms for constructing models

from data. Therefore, machine learning researchers

need to ﬁnd the means for assessing the perfor-

mance of different ML algorithms applied to common

datasets representing varying domains and degrees of

difﬁculty. Although much work in machine learning

has concentrated upon data without noise, real-world

data always have noise, with the most extreme form

being simply the absence of a measured value. In

consequence, interest has grown in ﬁnding new meth-

ods to cope with incomplete datasets and in assessing

those methods (e.g., (Onisko et al., 2002; Twala et al.,

2005; Twala et al., 2008)).

Absence of data values is ubiquitous in part be-

cause there are many ways in which measurements

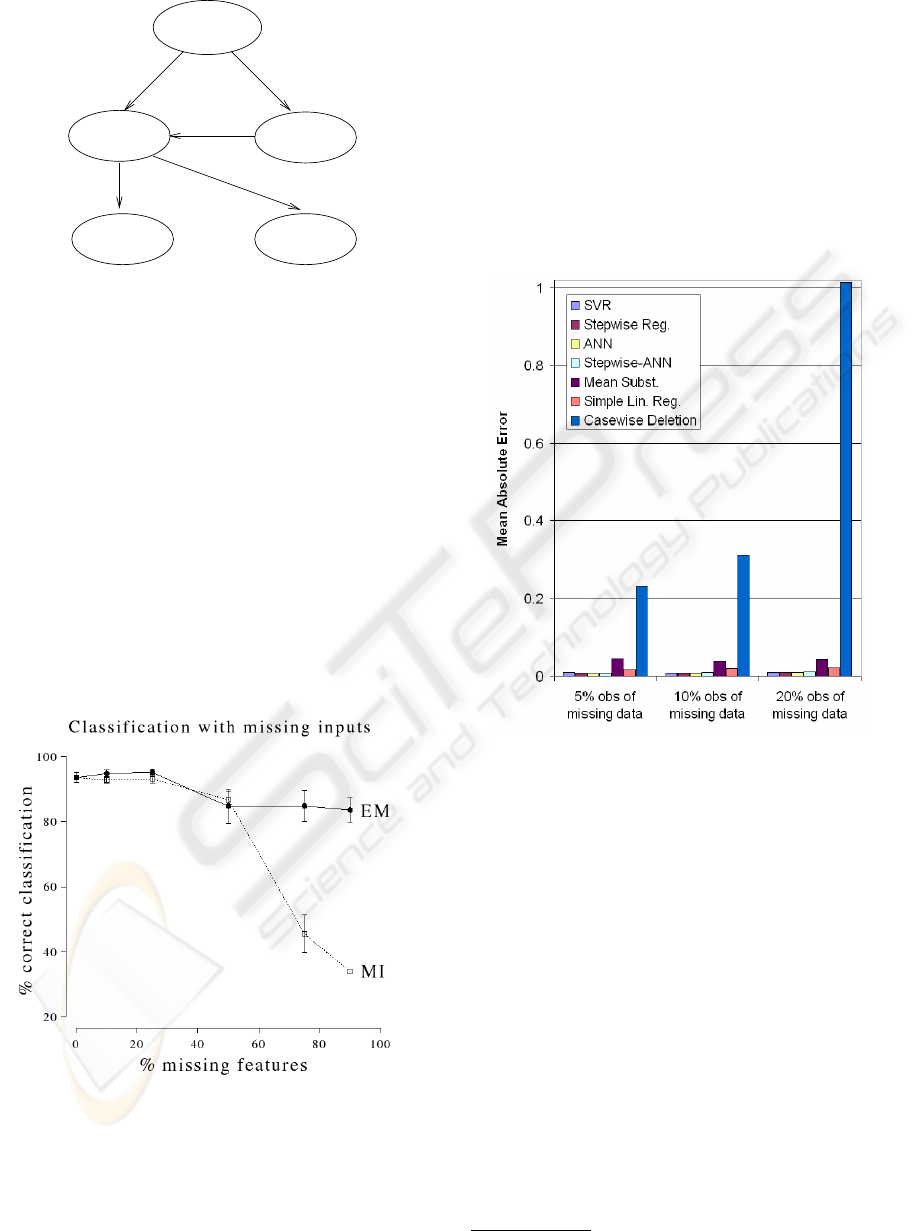
can fail. We illustrate with the simple causal Bayesian

network of Figure 1. We shall assume that joint ob-

servations of these variables come from sample sur-

veys, but similar failures to measure can arise from

any measurement technique. First, some missing val-

ues may arise simply from survey takers entirely over-

looking a question, independently of what the ques-

tion is about or the values of any variables. Second,

the failure to measure particular variables may de-

pend upon the values of other variables; for exam-

ple, it may turn out that lawyers as a class are less

inclined to reveal their incomes than people of other

occupations. Third, the failure to measure may be

sensitive additionally to the unmeasured value of the

variable at issue; for example, it may be that it is pri-

marily the wealthy lawyers who are reluctant to re-

veal their incomes. Following Rubin (Rubin, 1976),

it has become common to refer to these three mecha-

nisms for values to be missed as, respectively, missing

completely at random (MCAR), missing at random

(MAR) and not missing at random (NMAR). These

names are somewhat misleading, and we shall be-

low present reasons for adopting a more descriptive

nomenclature.

Given the prevalence of incompleteness in real

data, and its variety, it is important for ML researchers

to investigate how their various algorithms perform

given these different types of incomplete data. How-

ever, the missing mechanism for real data is most

likely unknown.

Wen Y., B. Korb K. and E. Nicholson A. (2009).

DATAZAPPER: GENERATING INCOMPLETE DATASETS.

In Proceedings of the International Conference on Agents and Artiﬁcial Intelligence, pages 69-76

DOI: 10.5220/0001660700690076

 SciTePress

age

house

income occupation

automobile

Figure 1: An example model.

Of course, ML researchers do undertake these

types of experiments with different missing data. For

example, Ghahramani and Jordan (Ghahramani and

Jordan, 1994) evaluated the performance of clas-

siﬁcation with missing data dealt by Expectation-

Maximization (EM) and mean imputation (IM) (see

Figure 2). Gill et al. (Gill et al., 2007) examined the

performance of learning algorithms between artiﬁcial

neural networks (ANNs) and support vector machines

(SVMs) on data MAR. Another example is Richman

et al. (Richman et al., 2007), who compared differ-

ent methods of handling missing value and presented

in terms of mean absolute error (MAE) in Figure 3.

They used real data with some values removed ran-

domly, that is, MCAR.

Figure 2: Example 1 of ML research on varying missing

values. Classiﬁcation of the iris data from (Ghahramani and

Jordan, 1994).

However, it is difﬁcult using only real data to

compare the performance of algorithms for machine

learning and methods for dealing with missing val-

ues, since the nature of the real system, including the

mechanisms whereby data go missing, is at issue; it is

difﬁcult or impossible to determine which algorithm

has produced a model closer to reality. For machine

learning research, we want to test against artiﬁcial

data generated from a known system with a known

mechanism causing values to go missing. This pro-

vides more ﬂexibility with the type of missing mech-

anisms, the type of datasets and the degree of depen-

dence. Moreover, performances can then be evaluated

against the true model.

Figure 3: Example 2 of ML research on varying missing

values. A bar chart illustrating the difference of variance

between the original and imputed data sets from (Richman

et al., 2007).

Here we present DataZapper, a versatile software

tool for generating artiﬁcial datasets with missing val-

ues. DataZapper renders some values in a dataset

absent according to speciﬁed conditions based upon

any variable and any value within that dataset; these

conditions can be tuned precisely for degrees of de-

pendence, allowing for systematic experimentation.

We shall make this tool available to machine learning

community via the Weka

machine learning platform.

One of our motivations in producing this tool is to en-

courage the machine learning community to explore

varieties of incompleteness beyond MCAR, which is

the only kind assumed by many algorithms, such as

the expectation maximization (EM) technique for re-

placing missing values in Weka. With a tool granting

easy access to more realistic forms of incompleteness

http://www.cs.waikto.ac.nz/ml/weka/

ICAART 2009 - International Conference on Agents and Artificial Intelligence

we expect more attention to them will be given.

The only previously reported tool we know of

for generating incomplete data is that of Francois

and Leray (Francois and Leray, 2007). They em-

ploy Bayesian networks (BNs) as a useful way to

generate artiﬁcial data with missing values. Unfor-

tunately, their tool is limited to MCAR and limited

forms of MAR incompleteness, with no ability to pro-

duce NMAR data. As Francois and Leray point out,

all of these forms of generating missing data can be

useful for generic software testing, beyond machine

learning research.

The structure of our paper is as follows. Section 2

describes the three absent data mechanisms and in-

troduces our nomenclature for them. In Section 3

we present a BNF (Backus-Naur Form (Backus and

Naur, 1960)) grammar for scripting DataZapper. In

Section 4 we present the details of DataZapper, in-

cluding data formats in Section 4.1 and an overview

of how it works in Section 4.2. Section 5 illustrates

DataZapper’s use in an experimental setting.

2 ABSENT DATA MECHANISMS

A dataset is a matrix in which rows represent the cases

(joint samples) and columns represent variables mea-

sured for each case. Ideally, a dataset has all the cells

ﬁlled—i.e., it is a complete data set. However, most

real datasets have some values unobserved—i.e., they

are incomplete.

As we mentioned, Rubin (Rubin, 1976) intro-

duced and named three types of missing data mech-

anisms. We shall now motivate the adoption of new

names for these. First, we prefer to talk of “absent

data” rather than “missing data”, for the simple but

sufﬁcient reason that “absent” has a natural nominal

form, “absence”, while “missing” leads to the awk-

ward neologism “missingness”. More signiﬁcantly,

two of Rubin’s labels are clearly inadequately de-

scriptive of the mechanisms involved:

Missing Completely at Random (MCAR): as the

absence of values is independent of all variable

values, including the value for this particular cell,

this label is actually appropriate. Therefore, we

propose calling these cases absent completely at

random (ACAR).

Missing at Random (MAR): these missing cases

have arbitrary dependencies upon the values of

other variables. In consequence, they may not

even be random at all, but functionally depen-

dent upon the values of other variables in extreme

cases. Hence, we prefer calling them absent un-

der dependence (AUD).

Not Missing at Random (NMAR): The natural

way of interpreting this phrase is by negating

the second kind of “missingness”, which would

be entirely wrong. This case is simply a gener-

alization of AUD, allowing the absence of data

to depend also upon the actual value which has

failed to be measured. Hence, we have absent

under self-dependence (AUSD).

We submit that the most common case in real data

is the case most commonly ignored, AUSD, where the

values going unmeasured depend both on the values

of some other variables and the absent values them-

selves, as in wealthy lawyers hiding their wealth.

3 SCRIPTING DATAZAPPER

The speciﬁcations for how the data should go miss-

ing are made in a simple scripting language, whose

BNF grammar is shown in Figure 4. These rules are

applied to a dataset ﬁle to generate a new dataset ﬁle

with some observed values replaced by a token in-

dicating absence. The basic form of a sentence is

that of an “if... then...” production rule. The an-

tecedent describes the dependencies that absence has

on variables and values in the system, while the con-

sequent lists the variables that take absent values on

these conditions and with what probability. If the an-

tecedent is empty, then the absent data generation is

unconditional—i.e., the data are ACAR in so far as

this production rule is concerned. If the consequent is

empty, then the absence mechanism is applied to all

variables in the dataset. When the data are AUD or

AUSD, the antecedent grammar rule speciﬁes which

variable(s) the absence depends upon and for what

values or value ranges. The effects of the script rules

are cumulative. The result is a language in which

any strength of dependence upon any set of variables

can be speciﬁed, and such dependencies may be com-

<m-statement> :: = if <antecedent> then <consequent>

<antecedent> ::= <condition>*

<variable> ::= alpha alphanum*

<range> ::= [ <value>, <value> ]

<value> ::= alpha alphanum* | number | symbol

<consequent> ::= ( <prob> ) <variable>*

<prob> ::= number

Figure 4: BNF grammar for generating absent data.

DATAZAPPER: GENERATING INCOMPLETE DATASETS

Table 1: Examples of complete data and corrupted data in Datazapper’s default format.

Complete data Corrupted data

5 5

10000 10000

E A B C D E A B C D

E0 A1 B1 C0 D1 E0 A1 B1 ? D1

E1 A0 B0 C1 D1 E1 A0 B0 C1 D1

E0 A1 B0 C1 D0 E0 A1 B0 C1 D0

E1 A1 B1 C0 D0 E1 ? B1 ? D0

E1 A0 B1 C1 D1 E1 A0 B1 C1 D1

... ...

bined arbitrarily. For example, “OR” can be repre-

sented by having two different conditions.

BNF:

1. if then (20)

2. if then (30) A C

3. if C in [?] then (40) E

4. if Gender in [F] Age in [10, 20] then (40) Income

5. if Gender in [F] Income in [70000, 90000] then (40)

Income

6. if A in [A1] B in [B1] then (60) A D

Explanation:

1. ACAR: every variable will have 20% of its values ab-

sent

2. ACAR: each of the variables “A” and “C” will have

30% of its values absent

3. AUD: variable “E” will have 40% of its values absent

when variable “C” takes the value “?”, namely variable

“C” is already absent

4. AUD: variable “Income” will have 40% of its values

absent when “Age” is between 10 and 20 (inclusive)

and “Gender” is “F”.

5. AUSD: variable “Income” will have 40% of its values

absent when variable “Gender” has value “F” and “In-

come” is between “70000” and “90000”

6. AUSD: variable “A” and “D” will both have 60% of

their values absent when variable “A” has value “A1”

and “B” has value “B1”

Figure 5: Examples of absent data speciﬁcation in the

DataZapper script language (above) with the corresponding

English descriptions (below).

Figure 5 shows some examples of the absent data

speciﬁcations, across the range of types, together with

a corresponding English description. Note that exam-

ple 6 is of a mixed type, producing AUD for variable

D and AUSD for variable A.

4 TECHNICAL DETAILS

4.1 Data Format

DataZapper accepts two data formats: a default

format and Weka’s (Witten and Frank, 2005) data

format—Attribute-Relation File Format (ARFF).

The default format is the data format used by the

BN learning software CaMML (Wallace et al., 1996),

Tetrad (Spirtes et al., 2000) and BNT (Leray and

Francois, 2004). (We describe how we used DataZap-

per for the empirical comparison of some of these

methods in Section 5.) An example of complete data

in the default format is shown on the left side in Table

1. The ﬁrst two lines are the number of variables and

the number of observations, respectively. The next

line lists the names of the variables in the dataset.

Columns are separated by tab. Consider again Exam-

ple 2 in Figure 5 above: “if then (30) A C”, the cor-

responding corrupted data after applying dataZapper

is given on the right side in Table 1, with the absent

values represented by “?” in the default data format.

(The token used to represent absence can be changed

from this default using a runtime parameter.)

DataZapper supports the ARFF format in order to

be compatible with the Weka machine learning plat-

form, which has become a standard toolkit for ML

studies (e.g. (Witten and Frank, 2005)). In Table 2 we

reproduce the above example in an ARFF ﬁle. Note

that an additional attribute for absent values must be

indicated for those variables which are consequents of

a DataZapper rule.

4.2 DataZapper Operation

DataZapper processes the absent data speciﬁcations

one line at a time. In processing each script com-

mand, DataZapper ﬁrst parses it, validating its syntax

http://www.cs.waikato.ac.nz/ml/weka/arff.html

ICAART 2009 - International Conference on Agents and Artificial Intelligence

Table 2: Examples of complete data and corrupted data in ARFF format.

Complete data Corrupted data

5 5

10000 10000

@RELATION input @RELATION input

@ATTRIBUTE E {E0,E1} @ATTRIBUTE E {E0,E1}

@ATTRIBUTE A {A0,A1} @ATTRIBUTE A {A0,A1,?}

@ATTRIBUTE B {B0,B1} @ATTRIBUTE B {B0,B1}

@ATTRIBUTE C {C0,C1} @ATTRIBUTE C {C0,C1,?}

@ATTRIBUTE D {D0,D1} @ATTRIBUTE D {D0,D1}

@DATA @DATA

E0,A1,B1,C0,D1,input E0,A1,B1,?,D1,input

E1,A0,B0,C1,D1,input E1,A0,B0,C1,D1,input

E0,A1,B0,C1,D0,input E0,A1,B0,C1,D0,input

E1,A1,B1,C0,D0,input E1,?,B1,?,D0,input

E1,A0,B1,C1,D1,input E1,A0,B1,C1,D1,input

... ...

Table 3: Examples of two corrupted datasets.

corrupted data 1 corrupted data 2

5 5

10000 10000

E A B C D E A B C D

E0 A1 B1 ? D1 E0 ? B1 C0 ?

E1 A0 B0 C1 D1 E1 A0 B0 C1 D1

E0 A1 B0 C1 D0 E0 A1 B0 C1 D0

E1 ? B1 ? D0 E1 ? B1 C0 ?

E1 A0 B1 C1 D1 E1 A0 B1 C1 D1

... ...

against the BNF grammar. It then makes some val-

ues in the complete data absent, using a uniform ran-

dom variate in comparison with the speciﬁed prob-

ability. DataZapper then writes the resultant incom-

plete dataset to an intermediate ﬁle. DataZapper em-

ulates parallelism by generating intermediate output

ﬁles for each such line and, in the end, merging the

intermediate ﬁles into a ﬁnal output ﬁle. In the merg-

ing process absent values dominate; that is, a value

ends up missing if it is missing in any intermediate

ﬁle. DataZapper ﬁnishes by generating a data report

on the ﬁnal dataset, comparing the proportions of ab-

sent values with the original dataset.

We will now look at these steps in more detail with

examples. (Details of the parser and the algorithms

can be found in (Wen et al., 2008)).

4.2.1 The Corrupted Data Generator

This is the key processing step that renders some val-

ues in the input data absent. The proportion of the

absence is applied to each selected target variable,

evenly distributed over all the relevant observations

for that variable – that is, those observations which

satisfy the dependency condition.

4.2.2 Merging Data Files

In this processing step, DataZapper merges multiple

corrupted datasets with the same variables and the

same number of observations. The datasets having a

common source, the only differences between them

are those required by processing distinct script ﬁle

commands. The merged data is a kind of union of the

corrupted datasets, with the absence of a value in any

cell forcing its absence in the ﬁnal output. If there

are many script commands being executed, or if the

initial input ﬁle itself contained incomplete data, then

the ﬁnal dataset may contain less information (more

absent values) than anticipated.

For example, consider again Examples 2 and 6

from Figure 5 for specifying absent data. Table 3 dis-

plays some examples from the two corrupted datasets

respectively, while Table 4 shows the same examples

in the ﬁnal merged corrupted dataset.

DATAZAPPER: GENERATING INCOMPLETE DATASETS

Final: 20.00% 12.64% 0.00% 5.14% 30.35%

Original: 0.00% 0.00% 0.00% 0.00% 0.00%

A B C D E

Overall:

6813 values are absent, 13.63% of all values.

5201 cases contain absent values, 52.01% of 10,000 total cases.

Content of script file:

Percent of absent values:

if then (20) E A

if A in [A1] then (30) B E

if (C) in [C0] D in [D1] then (20) D

Figure 6: Example of DataZapper’s absent data report.

Table 4: Merged data from the examples in Table 3.

corrupted data

10000

E A B C D

E0 ? B1 ? ?

E1 A0 B0 C1 D1

E0 A1 B0 C1 D0

E1 ? B1 ? ?

E1 A0 B1 C1 D1

...

4.2.3 Data Report

DataZapper presents a statistical summary of the in-

completeness of the ﬁnal dataset. Figure 6 gives an

example data report. This report can be used to ﬁne

tune the scripting rules in the event that the overall

sparseness of the data is unexpectedly high, possibly

due to the cumulative effect of multiple rules on some

variables.

5 APPLICATION

We now describe an application of DataZapper in

generating incomplete data for use in some of our ma-

chine learning research. The speciﬁc application is an

empirical comparison of the performance of causal

discovery algorithms in ﬁnding the causal Bayesian

network (a kind of directed acyclic graph, or DAG)

which has generated some observational data. The al-

gorithms under test were K2 (Cooper and Herskovits,

1991), GES (Greedy Equivalence Search) (Meek,

1997), and the PC algorithm from Tetrad (Spirtes

et al., 2000). The ﬁrst algorithm, K2, returns a single

DAG which ﬁts the data best.

The other two algo-

We have enhanced K2 by utilizing a Minimum

Weighted Spanning Tree algorithm as a preprocessing step

rithms return an equivalence class of DAGs (a pat-

tern); that is, a set of DAGs which all have equal

maximum-likelihood scores based upon any given

set of observational data (Chickering, 1995). In ef-

fect, these algorithms are asserting that all the DAGs

within the pattern are equally likely to be the source of

the observed data. In assessing such results, therefore,

we use a pattern-to-DAG conversion algorithm (Wen

and Korb, 2007) algorithm which returns two DAGs:

that nearest to the original causal Bayesian network

in structure (as measured in edit distance) and that

farthest from the original network. This provides a

range of performance for assessing such algorithms

(assuming that the data are artiﬁcial, of course, since

otherwise the original network is unknown).

The experiment we ran was a three dimensional

evaluation: we varied the algorithm, the proportion of

absence and the absent data mechanism as shown in

Figure 7.

10 30 50 70 90

40 6020 80

Dependence

ACAR

AUD

AUSD

Absent−Mechanism

GES

Algorithm

Figure 7: Three dimensional experimental design.

We used 50 sets of complete data generated from a

known Bayesian network. We then applied DataZap-

per to produce 3 × 9 incomplete datasets for each

complete dataset, given the three absence mecha-

nisms and 9 steps of proportion of absence, as shown

to produce the total ordering of variables that K2 demands.

ICAART 2009 - International Conference on Agents and Artificial Intelligence

0.5

1.5

2.5

3.5

90 percent

80 percent

70 percent

60 percent

50 percent

40 percent

30 percent

20 percent

10 percent

complete

average edit distance (50 sets of 1000 observation)

degree of absent dependence

Compare algorithms on data AUD with mode imputation

PCn

PCf

GESn

GESf

Figure 8: Example experimental results using DataZapper: comparison of 3 causal discovery algorithms, on data generate

with AUD absence mechanism, varying the degree of data completeness.

in Figure 7. We then designed comparison experi-

ments for different combinations of these experimen-

tal parameters.

For example, one experiment involved selecting

the absence mechanism and then comparing the per-

formance of the causal discovery algorithms given

varying proportion of absence. The results of this

particular experiment are shown in Figure 8. Here

the evaluation measure we used is the edit distance of

the learned BN to the true model—Figure 1, averaged

over the 50 datasets. For the PC and the GES algo-

rithms we report two results, one based on the DAG

within the pattern returned that is nearest to the true

model (PCn and GESn), another for the DAG within

the pattern that is farthest from the true model (PCf

and GESf). In this experiment we used one of the

simplest methods for handling absent values, namely

modal imputation (i.e., replacing each absence token

with the modal value for that variable). Results are

available for all ACAR, AUD and AUSD. Only AUD

is used as an example. Figure 8 shows that under these

circumstances the performances for PC and GES im-

prove as the data quality improves, while K2 appears

to be stuck. Overall, GESn shows the best perfor-

mance.

6 CONCLUSIONS

DataZapper is a powerful and ﬂexible tool for incom-

plete data generation, developed speciﬁcally for use

in research comparing machine learning algorithms.

DataZapper allows researchers to specify both the

amount of absent data and the nature of the dependen-

cies in generating the absent data, using simple con-

ditional rules. Multiple conditions of absence can be

described for each variable and for multiple variables,

which will be applied cumulatively by DataZapper to

the input dataset, which itself may be either complete

or already corrupt. DataZapper is the only tool which

can generate incomplete data for all types of absent

data mechanisms (ACAR, AUD or AUSD) and with

any degree of dependence. We offer it through Weka

in the hopes that methods of coping with more inter-

esting and difﬁcult varieties of incomplete data may

be investigated by the machine learning community.

REFERENCES

Backus, J. and Naur, P. (1960). Revised report on the al-

gorithmic language algol 60. Communications of the

ACM, 3(5):299–314.

Chickering, D. M. (1995). A tranformational characteri-

zation of equivalent Bayesian network structures. In

Besnard, P. and Hanks, S., editors, UAI95, pages 87–

98, San Francisco.

DATAZAPPER: GENERATING INCOMPLETE DATASETS

Cooper, G. F. and Herskovits, E. (1991). A Bayesian

method for constructing Bayesian belief networks

from databases. In In Proceedings of the Conference

on Uncertainty in AI, pages 86–94. San Mateo, CA:

Morgan Kaufmann.

Francois, O. and Leray, P. (2007). Generation of incomplete

test-data using bayesian networks. In Proceedings of

International Joint Conference on Neural Networks,

pages 12–17, Orlando, Florida, USA.

Ghahramani, Z. and Jordan, M. I. (1994). Learning from in-

complete data. Technical Report AIM-1509, Artiﬁcial

Intelligence laboraory and Center for Biological and

Computational Learning, Department of Brain and

Cognitive Sciences, Massachusetts Institute of Tech-

nology.

Gill, M. K., Asefa, T., Kaheil, Y., and McKee, M. (2007).

Effect of missing data on performance of learning al-

gorithms for hydrologic predictions: Implications to

an imputation technique. Water Resources Research,

43(W07416,).

Leray, P. and Francois, O. (2004). BNT structure learning

package: documentation and experiment s. Techni-

cal Report Laboratoire PSI - INSA Rouen-FRE CNRS

2645, Universit et INSA de Rouen.

Meek, C. (1997). Graphical Models: Selecting Causal and

Statistical Models. PhD thesis, Carnegie Mellon Uni-

versity.

Onisko, A., Druzdzel, M. J., and Wasyluk, H. (2002). An

experimental comparison of methods for handling in-

complete data in learning parameters of bayesian net-

works. In Proceedings of the IIS’2002 Symposium

on Intelligent Information Systems, pages 351–360.

Physica-Verlag.

Richman, M. B., Trafalis, T. B., and Adrianto, I. (2007).

Multiple imputation through machine learning algo-

rithms. In Artiﬁcial Intelligence and Climate Appli-

cations (Joint between 5th Conference on Applica-

tions of Artiﬁcial Intelligence in the Environmental

Sciences and 19th Conference on Climate Variability

and Change).

Rubin, D. B. (1976). Inference and missing data.

Biometrika, 63(3):581–592.

Spirtes, P., Glymour, C., and Scheines, R. (2000). Causa-

tion, Prediction, and Search. Cambridge, MA:MIT

Press, 2 edition.

Twala, B., Cartwright, M., and Shepperd, M. J. (2005).

Comparison of various methods for handling incom-

plete data in software engineering databases. In 2005

International Symposium on Empirical Software En-

gineering, pages 105–114, Noosa Heads, Australia.

Twala, B. E. T. H., Jones, M. C., and Hand, D. J. (2008).

Good methods for coping with missing data in deci-

sion trees. Pattern Recogn. Lett., 29(7):950–956.

Wallace, C., Korb, K. B., and Dai, H. (1996). Causal dis-

covery via MML. In Proceedings of the Thirteenth In-

ternational Conference on Machine Learning, pages

516–524. Morgan Kaufmann.

Wen, Y. and Korb, K. B. (2007). A heuristic algorithm

for pattern-to-dag conversion. In Proceedings of

IASTED International Conference on Artiﬁcial Intel-

ligence and Applications, pages 428–433.

Wen, Y., Korb, K. B., and Nicholson, A. E. (2008).

Datazapper: A tool for generating incomplete

datasets. Technical report, Bayesian Intelligence Pty

Ltd.

Witten, I. H. and Frank, E. (2005). Data Mining: Practi-

cal Machine Learning Tools and Techniques with Java

Implementations. Morgan Kaufmann, San Francisco,

CA, USA, 2 edition.

ICAART 2009 - International Conference on Agents and Artificial Intelligence