
UPDATING A LOGISTIC DISCRIMINATION RULE
Comparing Some Logistic Submodels in Credit-scoring
Farid Beninel† and Christophe Biernacki‡
†CREST-ENSAI & UMR 6086, Campus de Ker Lann, rue Blaise Pascal, 35170 Bruz, France
‡Universit
´
e Lille1, UFR de Math
´
ematiques & UMR 6524, 59655 Villeneuve d’Ascq, France
Keywords:
Credit scoring, Discriminant rule, Error rate, Learning sample, Logistic model, Misclassification rate, Gener-
alized discrimination, Updating a discriminant rule, Subpopulations mixture, Supervised classification.
Abstract:
Often a discriminant rule to predict individuals from a certain subpopulation is given, but the individuals to
predict belong to another subpopulation. Two distinct approaches are usually implemented. The first approach
is to apply the same discriminant rule for the two subpopulations. The second approach is to estimate a new
rule for the second subpopulation. The first classical approach does not take into account differences between
subpopulations. The second approach is not reliable in cases of few available individuals from the second
subpopulation. In this paper we develop an intermediate approach: we get a rule to predict in the second
population combining the experienced rule of the first population and the available learning sample from the
second. Different models combining the first rule and the labeled sample from the second population are
estimated and tested.
1 INTRODUCTION
Given a categorical target variable and a set of
covariates, we deal with the issue of predictive
discrimination in the context of a mixture of two
subpopulations. More precisely, we have to construct
a rule that assigns individuals from one subpopula-
tion, to one of prespecified set of classes based on
a vector of measurements (or covariates) taken on
those individuals. The available data consist in small
learning sample from the subpopulation to predict
and a discriminant rule on the second one.
Such a problem arises in various fields of ap-
plication. The particular problem which motivates
this work concerns the prediction of some particular
borrowers behavior in credit-scoring. Here, the con-
cerned particular borrowers are not customer of the
bank where the loan is demanded. Hence, in the first
subpopulation borrowers are customers and in the
second subpopulation borrowers are not customers.
The behavior is given by the target variable with
creditworthy and not-creditworthy as the prespecified
classes.
This work extends a realized work (Biernacki
et al., 2002) related to prediction of gender of birds
given their morphometric measures and generalizing
the Gaussian predictive discrimination method. In
such an application individuals are seabirds from
Calanectris Diomedea species and the mixture of the
two subpopulations results from subspecies Borealis
and Diomedea distinguished by their geographical
distribution (Thibault et al., 1997), (Bretagnolle et al.,
1998).
As it is well known that the geographical location
affects on measures of size (Zink and Remsen, 1986),
the use of classical predictive discrimination methods
for predicting gender of birds from different locations
is unreliable. Here, by classical methods, we mean
methods based on pure models (i.e., models more
adapted for an homogeneous population): Gaussian
discriminant analysis, logistic discriminant analysis,
neural networks, classification and regression trees. . .
It is therefore necessary to have a good dis-
criminant method which takes into account the
geographical location. So, in (Biernacki et al.,
2002), we introduced a discriminant rule based on a
Gaussian mixture model associated with the design
267
Beninel F. and Biernacki C. (2009).
UPDATING A LOGISTIC DISCRIMINATION RULE - Comparing Some Logistic Submodels in Credit-scoring.
In Proceedings of the International Conference on Agents and Artificial Intelligence, pages 267-274
DOI: 10.5220/0001662302670274
Copyright
c
SciTePress

vector of morphometric characteristics.
In our problem of credit scoring, the bank has to
predict the behavior of borrowers to pay back loan,
on the basis of variables description. For this second
example, the subpopulations result from differences
elsewhere: customers and not-customers. These
differences could influence (in addition to covariates)
the target variable. It is obvious that informations
related to customers are more reliable than those
related to not-customers. For example, the debt ratio
and expenditures may be underestimated among the
not-customers when requesting the loan.
An other example in credit scoring is when
subpopulations result from changes over time.
In this case, a first discriminant rule predicting
borrowers behaviour classes is built. Such a rule is
derived from the observation of borrowers over a
time interval [T,T + 1] (as from a population Ω). In
addition, when these individuals are observed again
over a new interval [T + τ,T + τ + 1] of the same
length (as from population Ω
∗
), another allocation
rule is often necessary.
Obviously, changes in the economic and social
environments could induce significant changes in
the population of borrowers and could affect the risk
credit.
As pointed out in (Tuffery, 2007), implementation
of an allocation rule devoted to the prediction of the
risk classes requires stability in the studied population
and in the distribution of the available covariates.
In the issue that we study, the two subpopulations
are not exchangeable i.e., there is an experienced
rule defined on a first subpopulation and a learning
sample of small size from some different second one.
Here, by allocation rule we mean a deci-
sion function Ψ
θ
= (ψ
θ1
,... ,ψ
θg
) (R
d
→ R
g
)
such that x ∈ R
d
is allocated to class with label
k
0
= argmax
k=1,...,g
ψ
θk
(x) where θ is the associated
parameter.
Usually, ψ
θk
(x) is a posterior probability to belong in
the class k or more generally, a corresponding score
(as the Anderson score, for example).
Hence, given a decision function or a classifier ψ
θ
,
one could consider that the experienced discriminant
rule on Ω is given unless we have the estimate
b
θ.
Then, the only remaining problem is to estimate the
parameter θ
∗
corresponding to the discriminant rule
on Ω
∗
.
Usually, two classical approaches are used to
obtain an estimation of θ
∗
: The first approach consists
in taking the same estimate than in Ω i.e.,
b
θ
∗
=
b
θ and
a the second approach in determining
b
θ
∗
using only
the learning sample S
∗
⊂ Ω
∗
.
If we denote by ν the number of components of θ
∗
,
one could present the first approach as leading to the
estimate
b
θ
∗
= g
1
(
b
θ) where g
1
= Id
ν
(R
ν
7→ R
ν
) and
the second one as leading to the estimate
b
θ
∗
= g
2
(S
∗
)
with g
2
(R
Card(S
∗
)×ν
7→ R
ν
).
The first approach does not take into account
the difference between the two subpopulations. The
second one needs a learning sample of a sufficient
size and here we deal with the problem of a small
one. This raises the problem of accuracy of the
estimate
b
θ
∗
= g
2
(S
∗
).
Thus, the problem here, is to take account of the char-
acteristics of the available sample as recommended
rightly by David Hand (Hand, 2005). He noted that
the advantage of an advanced method of modelling
relatively to a simple one (linear, for example) is
often in a better modeling of the study sample.
To circumvent the problem of specific data, we ex-
ploit the idea that information related to one of the two
subpopulations contains some information related to
the other. Thus, we search an acceptable relationship
between the two available distributions (i.e., the dis-
tribution of covariates on Ω and this one on Ω
∗
).
The relationship between distributions of covariates
on Ω and Ω
∗
induces a parametric relationship θ
∗
=
Φ
γ
(θ) between parameters.
The estimation method to derive θ
∗
is a plug in one
i.e., given the link function Φ
γ
and considering θ =
b
θ,
we use the learning sample S
∗
to estimate γ. The esti-
mate depends now on S
∗
and θ i.e.,
b
θ
∗
= Φ
b
γ(S
∗
)
(
b
θ) = g (
b
θ,S
∗
). (1)
The problem of the smallness of the sample S
∗
arises
again when estimating γ. However, the number of
components of γ should be much lower than those of
θ
∗
. Hence, this could be well appropriate.
In the case of the Gaussian mixture model, this
plug in approach appears very promising. In (Bier-
nacki et al., 2002) we introduced a somewhat simi-
lar plug in method to build a generalized discriminant
rule devoted to prediction on a Gaussian subpopula-
tion (i.e., the restriction of the covariates vector is a
Gaussian per class), learning on another one.
In this work, we extend this idea to the logistic dis-
criminant model i.e., for each of the two subpopu-
lations the response variable depends on covariates
ICAART 2009 - International Conference on Agents and Artificial Intelligence
268

according to a logistic model. θ and θ
∗
are respec-
tively the vectors of covariates (including intercept)
effect. The link between the two subpopulations con-
sists in a direct relationship between the parameters
i.e., θ
∗
= Φ
γ
(θ).
Given the function Φ
γ
, each system of constraints on
γ generates a logistic submodel. We focus on the esti-
mation of each logistic submodel and the comparison
of some of these submodels from the error-cost point
of view.
2 GENERALIZED LOGISTIC
DISCRIMINATION
2.1 The Logistic Model
Let x ∈ R
d
be a vector of covariates and an associated
response variable Y ∼ M
g
(1,π
1
,. .. ,π
g
) where g ≥ 2.
Let us set t
k
(x,θ) = P(Y = k|x; θ), with
θ = {(β
0k
||β
0
k
) ∈ R
d+1
,k = 1, .. ., g}. Here, (β
0k
||β
0
k
)
is the concatenation of the k
th
intercept and the k
th
vector of covariates effect.
The multinomial logistic model is defined by the
generalized logit given by the following equation
log
t
k
(x,θ)
t
g
(x,θ)
= β
0k
+ β
0
k
x. (2)
Equivalently, the model is defined by the probability
distribution of Y
|x
, given by
t
k
(x,θ) =
exp(β
0k
+ β
0
k
x)
1 +
∑
g−1
j=1
exp(β
0 j
+ β
0
j
x)
, k = 1,. .. ,g
(3)
and where (β
0g
||β
0
g
) is the null vector of R
d+1
.
The discriminant rule based on this probabilistic
model, in the case of uniform errors cost, consists
in assigning the observation x ∈ R
d
to the group
k
0
= argmax
k=1,...,g
t
k
(x,θ).
For the general case, including non uniform errors
cost, k
0
= argmin
l=1,...,g
{
∑
g
k=1
C(k|l)t
k
(x,θ)}, where
C(k|l) is the misallocation cost value, when assigning
an observation from class {Y = l} to class {Y = k}.
The aim of this communication is the study and
comparison of some logistic submodels (or con-
strained logistic models) resulting from situations
where one has an experienced rule to predict on a first
subpopulation, a small learning sample from the sec-
ond which contains the individuals to predict.
2.2 The Logistic Mixture Model
Let us denote
- Ω, Ω
∗
two subpopulations from a same population
and p, p
∗
the associated prior probabilities,
-
e
X ∈ R
d
the covariates vector observed over the
disjoint union Ω t Ω
∗
,
-
e
Y a categorical target variable.
We set (
e
X,
e
Y )
|Ω
= (X,Y ) and (
e
X,
e
Y )
|Ω
∗
= (X
∗
,Y
∗
) and
denote by (x,y), (x
∗
,y
∗
) their respective values.
Here, we consider the logistic model, over Ω, as given
by
Y ∼ M
g
(1,π
1
,. .. ,π
g
),
t
k
(x,θ) =
exp(β
0k
+β
0
k
x)
1+
∑
g−1
j=1
exp(β
0 j
+β
0
j
x)
,
(4)
and over Ω
∗
, by
Y
∗
∼ M
g
(1,π
∗
1
,. .. ,π
∗
g
),
t
∗
k
(x
∗
,θ
∗
) =
exp(β
∗
0k
+β
∗
0
k
x
∗
)
1+
∑
g−1
j=1
exp(β
∗
0 j
+β
∗
0
j
x
∗
)
,
(5)
where t
∗
k
(x
∗
,θ
∗
) = P(Y
∗
= k|x
∗
;θ
∗
).
Here we define the logistic mixture model as fol-
lows:
for
e
x ∈ R
d
, P(
e
Y = k|
e
x) = pt
k
(
e
x,θ) + p
∗
t
∗
k
(
e
x,θ
∗
).
(6)
When the subpopulation of an observation ω such
that
e
X(ω) =
e
x is unknown, its allocation (to the
appropriate class) requires parameters p, p
∗
,θ, θ
∗
.
In the problem we solve in this paper, we have
to predict individuals from Ω
∗
and so P(
e
Y = k|
e
x) =
t
∗
k
(
e
x,θ
∗
). Consequently, we have to use an allocation
rule which requires the only parameter θ
∗
.
2.3 Generalized Logistic Discrimination
Different problems of discrimination under the logis-
tic mixture model, could be studied. The resolution
of these problems depends on the relevance of the
available data. Particularly, we identify two problems:
A first problem is the simultaneous estimation
of θ and θ
∗
. A second problem is to estimate θ
∗
in
situations of a given θ.
The resolution of the first problem requires two
learning samples of sufficient size (one sample from
each subpopulation). While the second problem
requires only one of these samples, and this is the
problem we have to study.
UPDATING A LOGISTIC DISCRIMINATION RULE - Comparing Some Logistic Submodels in Credit-scoring
269

Specifically, we have already an allocation rule on
Ω (i.e., we have θ or more usually, a given estimate
b
θ
of θ) and we want to get a new rule to predict on Ω
∗
(i.e., to estimate θ
∗
) with as available data to estimate
a sample S
∗
= {(x
∗
i
,z
∗
i
) : i = 1,. .. ,n
∗
}.
The practice has resulted in the two following
cases:
case1. we have a unique population (i.e., we con-
sider Ω = Ω
∗
and therefore θ = θ
∗
),
case2. we detect the mixture i.e., we consider Ω 6=
Ω
∗
and we estimate θ
∗
using only S
∗
.
Finally, in these usual practices, it is believed to know
everything (case 1) or nothing on Ω
∗
(case 2). In
real problems links between subpopulations could ex-
ist and consequently, informations on Ω could provide
some information on Ω
∗
.
3 LINKS BETWEEN
SUBPOPULATIONS
3.1 Linear Links Models
In this work, we limit the study to the models defined
by a linear relationship between parameters θ
∗
and θ
i.e., for all k = 1,. ..,g − 1,
β
∗
0k
= α
k
+ β
0k
, β
∗
k
= Λ
k
β
k
, (7)
where α
k
∈ R and Λ
k
is a d × d diagonal matrix (or a
d dimensional vector).
Replacing β
∗
0k
and β
∗
k
in Equation (5) by their val-
ues given by the Equation (7), we obtain the new pa-
rameterisation
t
∗
k
(x
∗
,θ, γ) =
exp(β
0k
+ α
k
+ β
0
k
Λ
k
x
∗
)
1 +
∑
g−1
j=1
exp(β
0 j
+ α
j
+ β
0
j
Λ
j
x
∗
)
, (8)
where γ = {(α
k
||Λ
k
) ∈ R
d+1
: k = 1, .. ., g − 1}.
As it will be seen in subsection 3.2, linear link
models defined by Equations (7) are those obtained
when the random vectors X
|Y =k
, k = 1,. ..,g (resp.
X
∗
|Y
∗
=k
, k = 1, .. ., g ) are Gaussian homoscedastic.
The constrained situation where for all k, α
k
= 0
and Λ
k
= I
d
(the d-dimensional identity matrix),
returns case1 of the classical approach.
The situation where α
k
and Λ
k
are unconstrained,
returns case2.
We will compare these two classical situations to
intermediate parsimonious models. Thus, the purpose
of this communication is the estimation and the com-
parison of the models listed below:
(M1 ≡ case1) α
k
= 0 and Λ
k
= I
d
for all 1 ≤ k ≤
g − 1. The score functions are invariable.
(M2) α
k
= 0 and Λ
k
= λ
k
I
d
with λ
k
∈ R. Each
score function (corresponding to a fixed class)
changes w.r.t. λ
k
. The ranks corresponding to in-
dividual scores are invariant.
(M3) α
k
∈ R and Λ
k
= I
d
. The score functions
differ only w.r.t. the intercept and thus, changes
the threshold for assignment to classes. The dif-
ferences between scores and the corresponding
ranks are invariable.
(M4) α
k
∈ R and Λ
k
= λ
k
I
d
. Here the ranking of
the scores is invariable.
(M5) α
k
= 0 and Λ
k
∈ R
d
; the threshold is invari-
able but covariates coefficients could change.
(M6 ≡ case2) α
k
∈ R and Λ
k
∈ R
d
. All parame-
ters are free.
If we denote by ≺ the symbol of nesting between
models, we establish the partial ranking M1 ≺ M2 ≺
M5 ≺ M6 and M1 ≺ M3 ≺ M4 ≺ M6.
These relations are used to compare models with in-
formation criteria as the Schwarz criterion (BIC) or
the Akaike one (AIC) (Lebarbier and Mary-Huard,
2006).
3.2 Results from Homoscedastic
Gaussian Model
For each subpopulation the design vector is a mixture
of homoscedastic Gaussian distributions i.e.,
∀k = 1,. .. ,g X
|k
∼ N
d
(µ
k
,Σ) and X
∗
|k
∼ N
d
(µ
∗
k
,Σ
∗
).
The link between Ω and Ω
∗
is given by
X
∗
|k
d
= D
k
X
|k
+ b
k
, k = 1,. .. ,g, (9)
where D
k
is a diagonal real matrix. It’s known from
(De Meyer et al., 2000) that the link using a linear
function is the only link φ
k
= (φ
k1
,. .. ,φ
kd
) such that
X
∗
|k
d
= φ
k
(X
|k
) and which verifies the assumptions A1
and A2 that follow.
A1 : φ
k
is a component to component link i.e.,
function φ
k j
(R
d
7→ R) transforms the only j
th
component. Hence, we consider φ
k j
as an (R 7→
R) function.
A2 : φ
k j
is a C
1
function.
ICAART 2009 - International Conference on Agents and Artificial Intelligence
270

We derive from the Equation (9) the following rela-
tions between parameters of the two Gaussian distri-
butions.
µ
∗
k
= D
k
µ
k
+ b
k
, Σ
∗
k
= D
k
ΣD
k
. (10)
The matrices D
k
, allowing equal variances (see.
Equation (10)), are such that D
k
= A
k
D with D a
diagonal matrix and A
k
another diagonal matrix with
diagonal components in {−1,+1}.
We consider a link model as given by a set
{D,A
1
,. .. ,A
g
,b
1
,. .. ,b
g
}.
It is well known that there exists a particular link
between parameters of a generating Gaussian mixture
model and those of a the corresponding logistic one
(Anderson, 1982): for k = 1,. .. ,g, note f
k
the den-
sity function of the Gaussian distribution N
d
(µ
k
,Σ),
we have the Bayes formulae
P(Y = k|x) =
π
k
f
k
(x)
∑
g
j=1
π
j
f
j
(x)
. (11)
We derive the generalized logit (where g is the refer-
ence category)
log(
P(Y =k|x)
P(Y =g|x)
) = (µ
k
− µ
g
)
0
Σ
−1
x + log(
π
k
π
g
)
+
1
2
(kµ
g
k
2
Σ
−1
− kµ
k
k
2
Σ
−1
).
(12)
Consequently, the parameters given by the follow-
ing equations
β
0k
= log(
π
k
π
g
) +
1
2
(kµ
g
k
2
Σ
−1
− kµ
k
k
2
Σ
−1
),
β
k
= Σ
−1
(µ
k
− µ
g
).
(13)
are logistic parameters (corresponding to the intercept
and covariates effect).
In an analogous manner, the parameters of the lo-
gistic model derived from the Gaussian subpopulation
Ω
∗
, are
β
∗
0k
= log(
π
∗
k
π
∗
g
) +
1
2
(kµ
∗
g
k
2
Σ
∗−1
− kµ
∗
k
k
2
Σ
∗−1
),
β
∗
k
= Σ
∗−1
(µ
∗
k
− µ
∗
g
).
(14)
Using Equations (10) and setting D
k
= A
k
D
and b
k
= b, we establish for the model (of link)
(D,A
1
,. .. ,A
g
,b
1
,. .. ,b
g
), the equations returning the
link between parameters of the logistic models corre-
sponding to the two subpopulations. More precisely
β
∗
0k
= β
0k
+ α
k
,
β
∗
k
= A
k
Dβ
k
,
(15)
where α
k
= α(µ
k
,µ
g
,Σ, b,π
∗
k
,π
∗
g
) = log(
π
∗
k
π
∗
g
)+ <
µ
g
,D
−1
g
b >
Σ
−1
− < µ
k
,D
−1
k
b >
Σ
−1
.
4 PARAMETERS ESTIMATION
4.1 The Maximum Likelihood Method
The problem now is to estimate the parameters
γ = (α
1
,. .. ,α
g−1
,Λ
1
,. .. ,Λ
g−1
) involved in Equation
(8) giving, for an individual from Ω
∗
, the correspond-
ing probabilities of belonging to classes. The estima-
tion is based on sample S
∗
= {(Y
∗
i
,x
∗
i
) : i = 1,. .. ,n
∗
}.
We use the maximum likelihood estimator. The
conditional maximized likelihood is
L
Y
∗
|x
∗
(γ) =
n
∗
∏
i=1
g
∏
k=1
t
∗
k
(x
∗
i
,θ, γ)
Z
ik
, (16)
where Z
ik
= 1 if Y
∗
i
= k and 0 elsewhere.
That is to maximize the log-likelihood expressed by
the equation
L
Y
∗
|x
∗
(γ) =
∑
i:Z
ig
=1
log
1
1 +
∑
g−1
j=1
exp(h
j
(x
∗
i
))
!
+
∑
g−1
k=1
∑
i:Z
ik
=1
log
exp(h
k
(x
∗
i
))
1+
∑
g−1
j=1
exp(h
j
(x
∗
i
))
,
(17)
where h
k
is the k
th
Anderson score i.e.,
h
k
(x
∗
) = β
∗
0k
+ β
∗
0
k
x
∗
= β
0k
+ α
k
+ β
0
k
Λ
k
x
∗
.
According to the constraints imposed on γ, it leads
to a non-linear equations system. Table 1 gives for
each model (or each corresponding equations system)
the number of unknown parameters to estimate.
Table 1: Here, ν is the dimension of the estimated parameter
γ.
model M2 M3 M4 M5 M6
ν g − 1 g − 1 2g − 2 dg − d dg
In (Beninel and Biernacki, 2007), we give for the
case g = 2 , the system of likelihood equations, the
corresponding Hessian and condition of the unique-
ness of the solution. Here we treat the more com-
plex case g > 2, leading to a more complex non-linear
equations system, but without more difficulties from
the mathematical point of view.
UPDATING A LOGISTIC DISCRIMINATION RULE - Comparing Some Logistic Submodels in Credit-scoring
271

4.2 Using an Avalaible Logistic
Procedure
The estimation method could be reduced to the use of
an existing logistic procedure as the proc LOGISTIC
in SAS system. We present such a technique in the
context of a dichotomic response variable.
The unique Anderson score is
h(x
∗
) = β
0
+ α +
d
∑
j=1
λ
j
(β
j
x
∗ j
), (18)
where λ
j
is the j
th
diagonal component of matrix Λ,
β
j
and x
∗ j
respectively the j
th
component of β and of
the design vector x
∗
.
Let us set β
∗
0
= β
0
+ α and
e
x
∗
= β ∗ x
∗
the vec-
tor obtained using a component to component product
(or, Hadamard product) and
e
x
∗ j
its j
th
component.
e
X
∗
is the new design vector and we can view
e
x
∗
j
as
the j
th
weighted covariate. The score function given
by equation (18) is now written as
h(x
∗
) = β
∗
0
+
d
∑
j=1
λ
j
e
x
∗
j
, (19)
Consequently, for each model among M2, .. .,M6
we have to estimate (using an available logis-
tic procedure) γ = (β
∗
0
,λ
1
,. .. ,λ
d
) ∈ Γ ⊂ R
d+1
on the basis of the transformed learning sample
e
S
∗
= {(Y
∗
i
,
e
x
∗
i
) : i = 1,...,n
∗
}.
Depending on the model, the dimension of the pa-
rameters space Γ is variable. We explicit for each
model the numerical computation via the LOGISTIC
procedure.
We set z =
∑
d
j=1
e
x
∗ j
, corresponding to the Anderson
score related to the logistic model on Ω. We give in
the following the Anderson score on Ω
∗
, depending
on the transformed data.
M2 : We have to estimate the parameter λ ∈ R
such that
h(x
∗
) = β
0
+ λz, (20)
Here, the intercept is fixed as equal to β
0
.
M3 : We estimate the intecept β
∗
0
∈ R i.e.,
h(x
∗
) = β
∗
0
+ z. (21)
Here the effect of the covariate Z is constrained to
be equal to one.
M4 : We estimate (β
∗
0
,λ) ∈ R
2
such that
h(x
∗
) = β
∗
0
+ λz. (22)
We have to use the available logistic procedure
without constraints.
M5 : We have to estimate Λ
∗
∈ R
d
such that
h(x
∗
) = β
0
+ Λ
∗
e
x
∗
. (23)
The intercept is constrained to be equal to β
0
.
Here we consider model (M1) as the simplest model
and model (M6) as the more complex model.
When the response variable is polytomic (g > 2),
the number of possible constrained models is much
larger. For example for g = 3, we identify 15 sub-
models to compare.
5 NUMERICAL EXPERIMENTS
5.1 Data Description
The data are from a German bank and cover a sample
of 1000 consumer’s credits. Each of these consumer
is described by a binary response variable Kredit
({Kredit = 1} for credit-worthy or {Kredit = 0}
for not credit-worthy). In addition, 20 covariates
of different types (continuous, nominal, ordinal) as-
sumed to influence creditability are recorded. Exam-
ples of these covariates are:
Hoehe: the amount of credit in ”Deutche Mark”
[metrical],
Laufzeit: duration of credits in months [metri-
cal],
Laufkont: account balance [categorical],
Moral: behaviour repayment of other loans [cate-
gorical]. . .
For a complete access to these data we refer to the
book (Fahrmeir and Hamerle, 1984) or the current
website http://www.stat.uni-muenchen.de/
service/datenarchiv/Kredit.
These data are also described in the book of
(Fahrmeir and Tutz, 1994) (see. pages 31–34). The
prior probabilities corresponding to the categories
of the response variable are structurally unbal-
anced.Thus, for a consistent estimation of the logit
model the given sample is stratified (300 consumers
such that {Kredit = 0} and the remaining 700
consumers such that {Kredit = 1}.
These data are frequently used by specialists of
credit scoring when testing, calibrating and compar-
ing methods.
ICAART 2009 - International Conference on Agents and Artificial Intelligence
272

5.2 Covariates Selection
In order to evaluate the data quality and the influence
of the covariates (on creditability) a primary data pro-
cessing is realized including univariate and bivariate
statistics. Bivariate statistics measuring the depen-
dency between the selected covariates and the target
variable are computed.
This primary data processing highlights categories of
covariates with null frequencies of responses 0 or 1 of
the target variable. Such a characteristic in data cre-
ates the separability which implies divergence of the
likelihood maximization algorithm, when estimating
the parameters of the logistic model. In such a situ-
ation these categories are combined with close cate-
gories of the same covariate.
In addition, the primary data allows to determine co-
variates which influence the target variable. Thus,
logistic regression is tested with different combina-
tions of covariates among those appearing as jointly
influencing variable kredit. Like other authors, who
worked on these data, the more influencing covari-
ates are those introduced in section 5.1 and variables
Beszeit (present employement since) and Sparkont
(savings account).
Apart from Sparkont , the other covariates are un-
changed. In effect, to avoid the separability situation,
categories 4 and 5 of Sparkont are grouped together.
5.3 Subpopulations Definition
We use the variable Laufkont to carry out the separa-
tion in two subpopulations. The non-customers of the
bank(Laufkont = 1 ) constitute a subpopulation and
the customers (Laufkont > 1) constituting a second
subpopulation. Although laufkont is a covariate, we
use it to define the two subpopulations and avoid bias
of the difference in the amount and reliability of data
related to the two subpopulations.
5.4 Experiments Description
We implement in SAS the program hat manages data
and estimate the models. The implementation of these
models extending logistic regression is as follows:
Step 1: We apply the logistic regression with as pri-
mary data the design matrix related to customers (or
the learning sample S
L
⊂ Ω). The obtained estimate
θ is used to compute the new covariates subject to
step2: The continuous covariates are multiplied by
corresponding component of θ and binary covariates
(or categories of qualitative variables) are multiplied
by the corresponding parameter.
Step 2: The second step consists in the estimation
of parameters related to models M2 to M6. Such
an estimation is based on a learning sample S
∗
∈ Ω
∗
.
Sample S
∗
is derived (from non-customers) using the
surveyselect procedure to obtain a stratified ran-
dom sample. Percentages of responses {kredit = 1}
and {kredit = 0} are close to that ones of Ω
∗
.
Given the sample size, the simulations are to draw
B samples S
∗
from non-customers to estimate the 5
models and for each of S
∗
corresponds a test sample
S
∗
T
of the remaining non-customers.
Let C (l|k) denote the cost of misallocation of a bor-
rower from {Y
∗
i
= k} into {Y
∗
i
= l}, k,l = 0, 1. Let us
set ρ(1,0) =
C(1|0)
C(0|1)
, corresponding to error costs ra-
tio. Under acceptable assumptions related to the prior
probabilities p
0
, p
1
and for each fixed pair (S
∗
,S
∗
T
) we
estimate the exact error-rate of assignation to classes
given by
C(0|1)P(
c
Y
∗
= 0|Y
∗
= 1) +C(1|0)P(
c
Y
∗
= 1|Y
∗
= 0)
(or without loss, P(
c
Y
∗
= 0|Y
∗
= 1) + ρ(0,1)P(
c
Y
∗
=
1|Y
∗
= 0)).
For fixed ρ(1,0), p1, p0 , we get at B = 30 iterations
a stratified random sample of frequencies (n
0
,n
1
) (n
0
the number of responses {kredit = 0} in the learning
sample and n
1
the number of responses {kredit =
1}.
From Figure A.1, it appears that the ranks of BIC
values do not depends on ρ(1,0) values. Models M3,
M4 seem the best models (to generate data) among
M1,. .. ,M6.
Figure A.2, below gives the mean risk according to
the costs ratio. The sample size here is set at n
0
=
n
1
= 20.
For all values of ρ(1, 0), models M2 and M5 appear
the best ones, from the risk point of view. The most
practiced model M1, is very bad.
6 CONCLUSIONS
The simulations confirm the difference between sub-
populations. It appears that the best models from the
cost point of view (M2 and M5), are not the generat-
ing best models. Indeed, models M3 and M4 mini-
mize the BIC criterion.
The models M2 and M5 are those who move the in-
tercept. This coincides with the fact that for stratified
samples (as here), instead of the estimation of the in-
tercept β
∗
0
, one estimates β
∗
0
± log (πn
0
/(1 − π)n
1
).
In this work, the use of estimated logistic discriminant
rule is simple from the programming point of view as
we adapt an existing SAS procedure.
UPDATING A LOGISTIC DISCRIMINATION RULE - Comparing Some Logistic Submodels in Credit-scoring
273
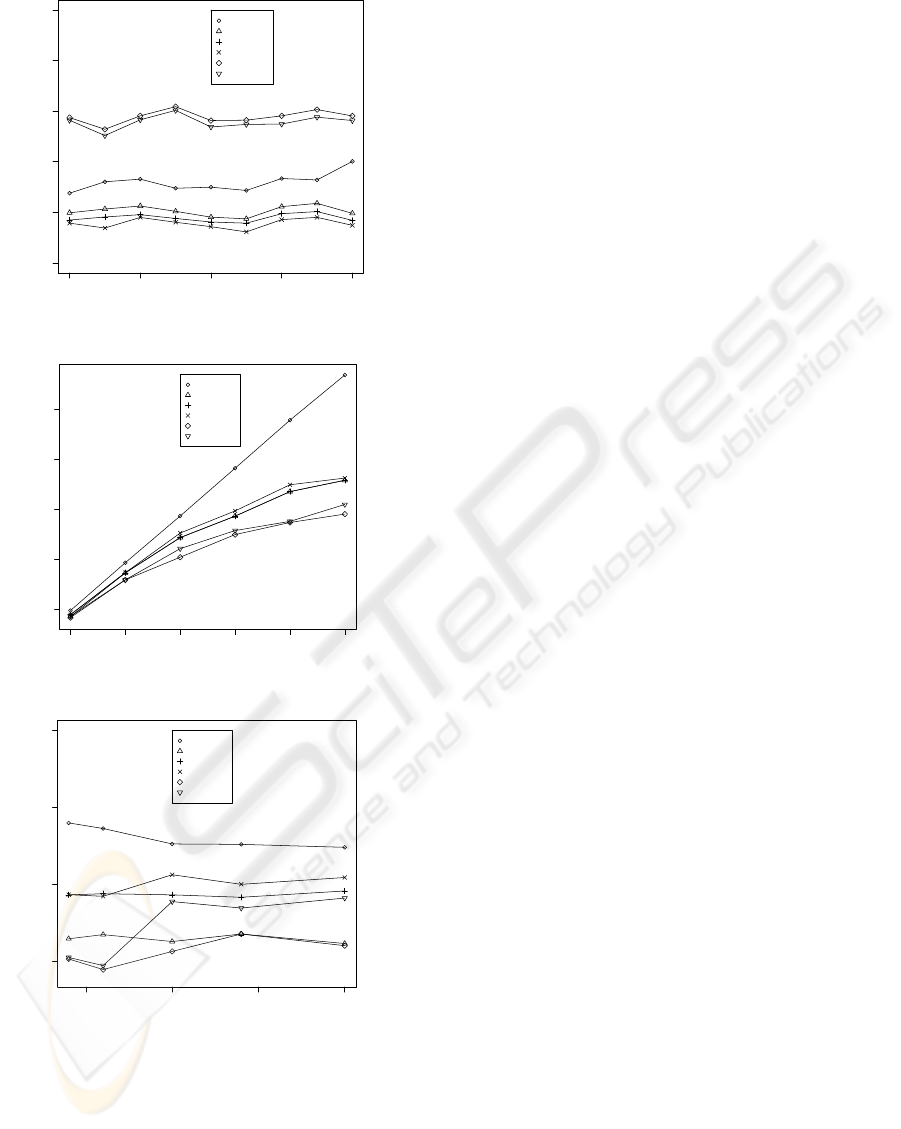
0.2 0.4 0.6 0.8 1.0
50 60 70 80 90 100
Cost report
mean BIC
Model M1
Model M2
Model M3
Model M4
Model M5
Model M6
Figure 1: Mean BIC value depending on ρ(1,0) value.
0.1 0.2 0.3 0.4 0.5 0.6
0.1 0.2 0.3 0.4 0.5
Cost report
mean risk
Model M1
Model M2
Model M3
Model M4
Model M5
Model M6
Figure 2: Mean risk value depending on ρ(1,0) value.
50 100 150 200
0.20 0.25 0.30 0.35
Sample size
Mean risk
Model M1
Model M2
Model M3
Model M4
Model M5
Model M6
Figure 3: Mean Risk value depending on the learning sam-
ple size value.
REFERENCES
Anderson, J. A. (1982). Logistic discrimination. In Hand-
book of Statistics (Vol. 2), P.R. Krishnaiah and L.
Kanal (Eds.). Amsterdam: North Holland, pages 169–
191.
Beninel, F. and Biernacki, C. (2007). Relaxations de la
r
´
egression logistique: mod
`
eles pour l’apprentissage
sur une sous-population et la pr
´
ediction sur une autre.
RNTI, A1:207–218.
Biernacki, C., Beninel, F., and Bretagnolle, V. (2002). A
generalized discriminant rule when training popula-
tion and test population differ on their descriptive pa-
rameters. Biometrics, 58:387–397.
Bretagnolle, V., Genevois, F., and Mougeot, F. (1998). Intra
and intersexual function in the call of a non passerine
bird. Behaviour, 135:1161–1202.
De Meyer, B., Roynette, B., Vallois, P., and Yor, M. (2000).
On independent times and positions for brownian mo-
tion. Institut Elie Cartan, 1.
Fahrmeir, L. and Hamerle, A. (1984). Multivariate statis-
tiche Verfahren. De Gruyter, Berlin.
Fahrmeir, L. and Tutz, G. (1994). Multivariate Statisti-
cal Modelling Based on Generalized Linear Models.
Springer Series in Statistics. Springer-Verlag, New
York.
Hand, D. J. (2005). Classifier technology and the illusion of
progress. Technical Report, Imperial college, London.
Lebarbier, E. and Mary-Huard, T. (2006). Une introduc-
tion au crit
`
ere bic : fondements th
´
eoriques et in-
terpr
´
etation. JSFDS, 147(1):39–57.
Thibault, J. C., Bretagnolle, V., and Rabouam, C. (1997).
Cory’s shearwater calonectris diomedia. Birds of
Western Paleartic Update, 1:75–98.
Tuffery, S. (2007). Am
´
eliorer les performances d’un
mod
`
ele pr
´
edictif: perspectives et r
´
ealit
´
e. RNTI,
A(1):42–74.
Zink, R. and Remsen, J. (1986). Evolutionary processes
and patterns of geographic variation in birds. Current
Ornithology, 4:1–69.
ICAART 2009 - International Conference on Agents and Artificial Intelligence
274
