QUALITY OF KNOWLEDGE IN GROUP DECISION SUPPORT

SYSTEMS

Luís Lima, Ricardo Costa

College of Management and Technology, Polytechnic of Porto, Felgueiras, Portugal

Paulo Novais, Cesar Analide, José Neves

Departamento de Informática / CCTC, Universidade do Minho, Braga, Portugal

José Bulas Cruz

University of Trás-os-Montes e Alto Douro, Vila Real, Portugal

Keywords: Incomplete information, Knowledge representation, Group decision support system, Idea generation and

argumentation.

Abstract: In this work it is addressed the problem of knowledge evaluation in a VirtualECare Group Decision

Supporting System (GDSS), in terms of an Multi-valued Extended Logic Programming language, which is

aimed at sustaining online healthcare services. Indeed, reasoning with incomplete and uncertain knowledge

have to be dealt with, due to the particular nature of the healthcare services, where the awful consequences

of bad decisions, or lack of timely ones, demand for a responsible answer.

1 INTRODUCTION

In the last years, we have assisted to a growing

interest in combining the advances in information

society - computing, telecommunications and

presentation – in order to create Group Decision

Support Systems (GDSS). Effective planning

depends on the generation and analysis of ideas

(innovative or not) and, for this reason, the idea

generation and management processes become a

crucial tool in present days. GDSS are interactive

computer-based systems aimed to help decision

makers use communication technologies,

information (structured or unstructured), knowledge

and/or models to solve problems and make

decisions, i.e., GDSS tend to be computer programs

that recurring to singular techniques may help, as the

name point out, in the decision making processes

(Parsons, 1996). Good decision making is an

essential skill in any environment, and in particular

in a healthcare one. Indeed, if you can learn to make

timely and well-considered decisions, then you can

lead. However, if you make poor decisions, your risk

of failure and your time may, most likely, be short

(Eysenbach, 2007) (Costa et al, 2007).

1.1 Group Decision Support System

It is expected that knowledge-driven GDSS will be

more comprehensive, cover broader domains and

give better advice (Power, 2007) and will also

benefit from progress in research areas of

organizational decision making, behavioral decision

theory and organizational behavior (Conklin, 2001)

(Conklin, 2006).

Our objective is to apply the above presented

GDSS, with the necessary change in order to

understating uncertainty an quality of information, to

a new sector. We believe the use of GDSS in the

Healthcare sector will allow professionals to achieve

better results in the analysis of one’s Electronic

Health Record (EHR) (According to ISO/DTR

20514:2005, EHR means a repository of patient data

in digital form, stored and exchanged securely, and

accessible by multiple authorized users).

This achievement is vital, regarding the

explosion of knowledge and skills, together with the

101

Lima L., Costa R., Novais P., Analide C., Neves J. and Bulas Cruz J. (2009).

QUALITY OF KNOWLEDGE IN GROUP DECISION SUPPORT SYSTEMS.

In Proceedings of the International Conference on Agents and Artiﬁcial Intelligence, pages 101-106

DOI: 10.5220/0001663501010106

 SciTePress

growing need to use limited resources more

efficiently.

Figure 1: VirtualECare Environment.

1.2 Idea Generation

and Argumentation

The Group Decision module (Figure 1 and Figure 2),

as stated above, is a major module of the

VirtualECare project. This fact, associated with the

importance of decision-making in today business

activity and with the needed celerity in obtaining a

decision in the majority of the cases that this key

module will be defied to resolve, requires a real

effectiveness of the decision making process. Thus,

the need for an Idea Generation tool that will support

the meetings of the group decision participants,

being those face-to-face, asynchronous or

distributed, becomes crucial.

The flow of new ideas is central in an

environment as the one presented above and after

establishing individual ideas the participants are

expected to “defend” those ideas in order to reach

consensus or majority. Each participant will,

therefore, and in a natural way, argue for the most

interesting alternatives or against the worst

alternatives, according to his/her preferences and/or

skills, thus, by expressing their arguments,

participants expect to influence the others’ opinions

and make them change their own (Brito et al, 2003).

In order to make this meetings as productive as

possible, participants must be kept updated, not

only, with all the existing information but also with

the respective quality measure and uncertain level.

We organize the paper as follows: First, we

briefly present the VirtualECare environment. In

Section 2 we discuss the knowledge representation

and reasoning procedures in the context of the

Extended Logic Programming language.

Figure 2: Group Decision Module Architecture.

In Section 3 we elaborate about the calculus for

computing the Quality of Knowledge embodied in a

logic theory or program. Finally, we presented the

conclusions and foresee future work.

2 KNOWLEDGE

REPRESENTATION AND

REASONING

The knowledge representation in a knowledge-

driven group decision support system is nuclear to

the success of the overall operation (Way, 1991),

(Analide et al., 2006), (Ginsberg, 1991).

A suitable representation of incomplete

information and uncertainty is needed, one that

supports non-monotonic reasoning. Historically,

uncertain reasoning has been associated with

Probability Theory, embodying non-Bayesian

theories of subjective probability, as in the

Dempster-Shafer Theory (Shafer, 1992). The

Dempster-Shafter Theory is well-known for its

usefulness to express uncertain judgments of

experts. This theory introduces the concept of belief

functions and is based on two ideas: (i) obtaining

degrees of belief for one question from subjective

probabilities for a related question, and (ii)

Dempster's rule for combining such degrees of belief

when they are based on independent items of

evidence. However, the use of belief functions may

involve challenging computational problems. Beliefs

are also represented in other contexts, for example

multi-agent systems, where specialized classes are

used to model a way of things, proposition or other

information relevant to the system and its mental

model (Cervenka and Trencansky, 2007). Another

promising computational paradigm, Abductive

ICAART 2009 - International Conference on Agents and Artificial Intelligence

102

Logic Programming (ALP) (Denecker and Kakas,

2002) has been recognized as a way to resolve some

limitations of logic programming with respect to

higher level knowledge representation and reasoning

tasks. Abduction is a way of reasoning on

incomplete or uncertain knowledge, in the form of

hypothetical reasoning, more appropriate to model

generation and satisfiability checking.

In a classical logical theory, the proof of a

theorem results in a true or false truth value, or is

made in terms of representing something, with

respect to one may not be conclusive. In opposition,

in a logic program, the answer to a question is only

of two types: true or false. This is a consequence of

the limitations of the knowledge representation in a

logic program, because it is not allowed explicit

representation of negative information. Additionally,

the operational semantics applies the Closed-World

Assumption (CWA) (Hustadt, 1994) to all the

predicates. The generality of logic programs

represents implicitly negative information, assuming

the application of reasoning according to the CWA.

An extended logic program, on the other hand, is

a finite collection of rules of the form (Neves, 1984)

(Gelfond and Lisfschitz, 1990):

nmmm

pnotpnotppq

∧∧∧∧∧← ......

(1)

∧...∧

∧not

m+1

∧...∧not

(2)

where ? is a domain atom denoting falsity, the pi,

qj, and p are classical ground literals, i.e. either

positive atoms or atoms preceded by the classical

negation sign ¬. Every program is associated with a

set of abducibles. Abducibles can be seen as

hypotheses that provide possible solutions or

explanations of given queries, being given here in

the form of exceptions to the extensions of the

predicates that make the program.

The objective is to provide expressive power for

representing explicitly negative information, as well

as directly describe the CWA for some predicates,

also known as predicate circumscription (Parsons,

1996). Three types of answers to a given question

are then possible: true, false and unknown. The

representation of null values will be scoped by the

ELP. In this work, we will consider two types of null

values: the first will allow for the representation of

unknown values, not necessarily from a given set of

values, and the second will represent unknown

values from a given set of possible values. We will

show now how null values can be used to represent

unknown information. In the following, we consider

the extensions of the predicates that represent some

of the properties of the participants, as a measure of

their skills for the decision making process:

area_of_expertise: Entities x StrValue

role: Entities x StrValue

credible: Entities x Value

reputed: Entities x Value

The first argument denotes the participant and

the second represents the value of the property (e.g.,

credible (luis, 100) means that the

credibility of the participant luis has the value

100).

credible(luis,100)

¬credible(E,V)←

not credible(E,V)

Program 1: Extension of the predicate that states the

credibility of a participant.

In Program 1, the symbol ¬ represents the strong

negation, denoting what should be interpreted as

false, and the term not designates negation-by-

failure.

Let us now admit that the credibility of another

possible participant ricardo has not, yet, been

established. This will be denoted by a null value, of

the type unknown, and represents the situation in

Program 2: the participant is credible but it is not

possible to be certain (affirmative) about its value.

credible(luis,100)

credible(ricardo,⊥)

¬credible(E,V)←

not credible(E,V),

not exception(credible(E,V))

exception(credible(E,V))←

credible(E,⊥)

Program 2: Credibility about participant Ricardo, with an

unknown value.

In the second clause of Program 2, the symbol ⊥

represents a null value of an undefined type. It is a

representation that assumes any value as a viable

solution, but without being given a clue to conclude

about which value one is speaking about. It is not

possible to compute, from the positive information,

the value of the credibility of the participant ricardo.

The fourth clause of Program 2 (the closure of

predicate credibility) discards the possibility of

being assumed as false any question on the specific

value of credibility for participant ricardo.

Let’s now consider the case in which the value of

the credibility of a participant is foreseen to be 60,

with a margin of mistake of 15. It is not possible to

be positive, concerning the credibility value.

However, it is false that the participant has a

QUALITY OF KNOWLEDGE IN GROUP DECISION SUPPORT SYSTEMS

103

credibility value of 80 or 100. This example suggests

that the lack of knowledge may only be associated to

a enumerated set of possible known values. As a

different case, let’s consider the credibility of the

participant paulo, that is unknown, but one knows

that it is specifically 30 or 50.

credible(luis,100)

credible(ricardo,⊥)

¬credible(E,V)←

not credible(E,V),

not exception(credible(E,V))

exception(credible(E,V))←

credible(E,⊥)

exception(credible(carlos,V))←

≥ 45 ∧ V ≤ 75

exception(credible(paulo,30))

exception(credible(paulo,50))

Program 3: Representation of the credibility of the

participants Carlos and Paulo.

Using Extended Logic Programming, as the logic

programming language, a procedure given in terms

of the extension of a predicate called demo is

presented here. This predicate allows one to reason

about the body of knowledge presented in a

particular domain, set on the formalism previously

referred to. Given a question, it returns a solution

based on a set of assumptions. This meta predicate is

defined as: Demo: Question x Answer

Where Question indicates a theorem to be proved

and Answer denotes a truth value (see Program 4):

true (T), false (F) or unknown (U).

demo(Q,T)← Q

demo(Q,F)← ¬Q

demo(Q,U)← not Q ∧ not ¬Q

Program 4: Extension of meta-predicate demo.

3 QUALITY OF KNOWLEDGE

In a majority of situations, the trigger to make a

decision is the time period to the decision. It is

reasonable to argue that, in any decision making

process, the decision is made without having all the

information pertaining to the problem. When the

decision maker reaches the time limit, he/she makes

the decision using the available information, to the

best of his/her knowledge.

How does a decision maker is confident about

the reliability of the information at hand? In group

decisions the situation is more complex: each person

that participates in the final decision must be

confident on: The reliability of the computer support

system; The other decision makers; The information

rolling in and out of the system and the information

exchanged between participants.

The Group Decision of the VirtualECare system

above operates in an such environment.We leave the

first issue to others and concentrate in the last two,

proposing a model for computing the quality of

knowledge.

Let i (i ∈ 1,…, m) represent the predicates whose

extensions make an extended logic program that

models the universe of discourse and j (j ∈ 1,…, n)

the attributes of those predicates. Let x

∈ [min

max

] be a value for attribute j. To each predicate is

also associated a scoring function V

[min

, max

] →

0 … 1, that gives the score predicate i assigns to a

value of attribute j in the range of its acceptable

values, i.e., its domain (for simplicity, scores are

kept in the interval [0 … 1]), here given in the form:

all(attribute_exception_list,

sub_expression, invariants)

This denotes that sub_expression should hold for

each combination of the exceptions of the extensions

of the predicates that represent the attributes in the

attribute_exception_list and the invariants.

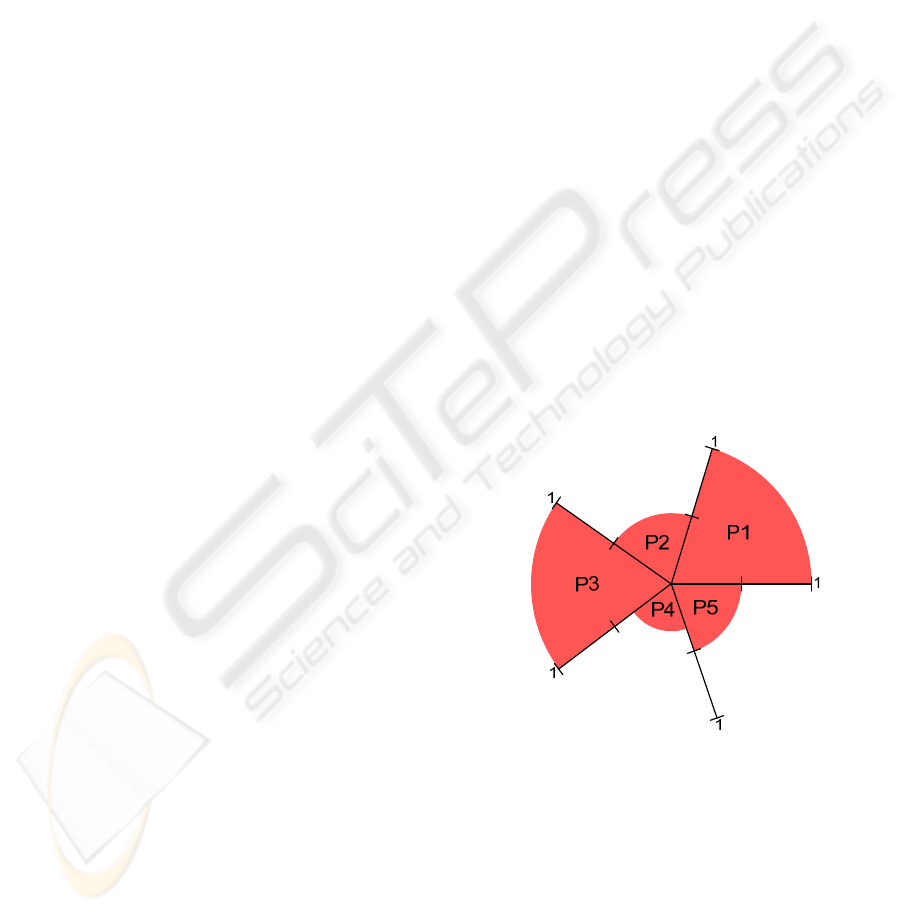
Figure 3: A measure of the quality of knowledge for a

logic program or theory P.

This is further translated by introducing three

new predicates. The first predicate creates a list of

all possible exception combinations (pairs, triples,

..., n-tuples) as a list of sets determined by the

domain size (and the invariants). The second

predicate recurses through this list and makes a call

to the third predicate for each exception

combination. The third predicate denotes

sub_expression, giving for each predicate, as a

ICAART 2009 - International Conference on Agents and Artificial Intelligence

104

result, the respective score function. The Quality of

Knowledge (QK) with respect to a generic predicate

P is therefore given by QK

= 1/Card, where Card

denotes the cardinality of the exception set for P, if

the exception set is disjoint. If the exception set is

not disjoint, the quality of information is given by:

Card

(3)

where

Card

C is a card-combination subset, with

Card elements.

The next element of the model to be considered

is the relative importance that a predicate assigns to

each of its attributes under observation: w

stands for

the relevance of attribute j for predicate i (it is also

assumed that the weights of all predicates are

normalized, i.e.:

∑

=∀

(4)

It is now possible to define a predicate’s scoring

function, i.e., for a value x = (x

, ..., n) in the multi

dimensional space defined by the attributes domains,

which is given in the form:

∑

∗=

jijiji

xVwxV

)()(

(5)

It is now possible to measure the QK that occurs

as a result of a logic program, by posting the V

(x)

values into a multi-dimensional space and projecting

it onto a two dimensional one.

Using this procedure, it is defined a circle, as the

one given in Figure 3. Here, the dashed n-slices of

the circle (in this example built on the extensions of

five predicates, named as p

... p

) denote de QK that

is associated with each of the predicate extensions

that make the logic program. It is now possible to

return to our case above and evaluate the global

credibility of the system. Let us consider the logic

program (Program 5).

¬credible(E,V)← not credible(E,V),

not exception(credible(E,V))

exception(credible(E,V))←

credible(E,⊥)

credible(luis,100)

credible(ricardo,⊥)

exception(credible(carlos,V))←

≥ 45 ∧ V ≤ 75

exception(credible(paulo,30))

exception(credible(paulo,50))

¬role(E,V)← not role(E,V),

not exception(role(E,V))

role(luis,⊥)

role(ricardo,doctor)

exception(role(carlos,doctor))

¬reputed(E,V)← not reputed(E,V),

not exception(reputed(E,V))

exception(reputed(luis,80))

exception(reputed(luis,50))

exception(reputed(ricardo,40))

exception(reputed(ricardo,60))

reputed(carlos,100)

Program 5: Example of universe of discourse.

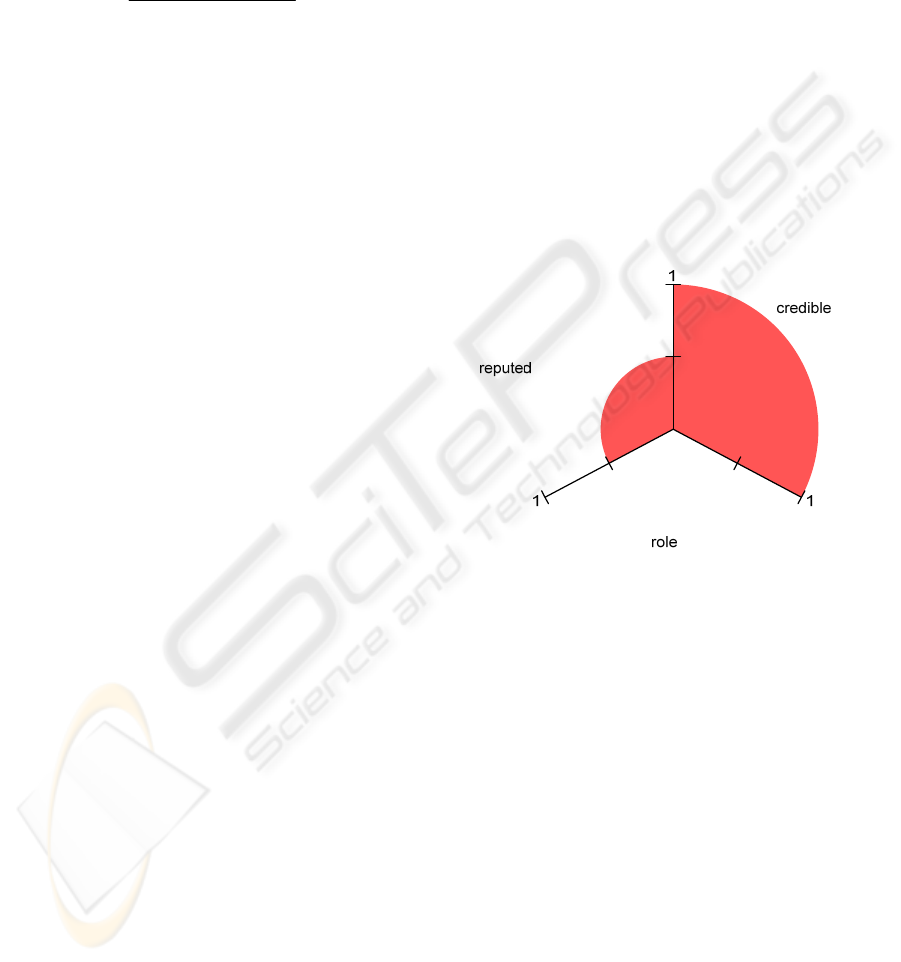
As an example we represent the QK associated

with participants luis and ricardo, depicted in

Figures 4 and 5.

In order to find the relationships among the

extensions of these predicates, we evaluate the

relevance of the QK, given in the form

credible

(luis) = 1;V

reputed

(luis) = 0.785; V

role

(luis) = 0.

Figure 4: A measure of quality of knowledge about

participant luis.

It is now possible to measure the QK associated

to a logic program referred to above: the shaded n-

slices (here n is equal to three) of the circle denote

the QK for predicates credible, reputed and role.

Besides being able to evaluate the quality of

individual actors and individual pieces of

information that flows in a group decision system,

we aim to have an overall mechanism that allows

one to measure the global quality of the system itself

and, consequently, the outcomes from it. The same

mechanism used to evaluate individual parts of the

system is consistently used to evaluate all the

system, through an extension process.

QUALITY OF KNOWLEDGE IN GROUP DECISION SUPPORT SYSTEMS

105

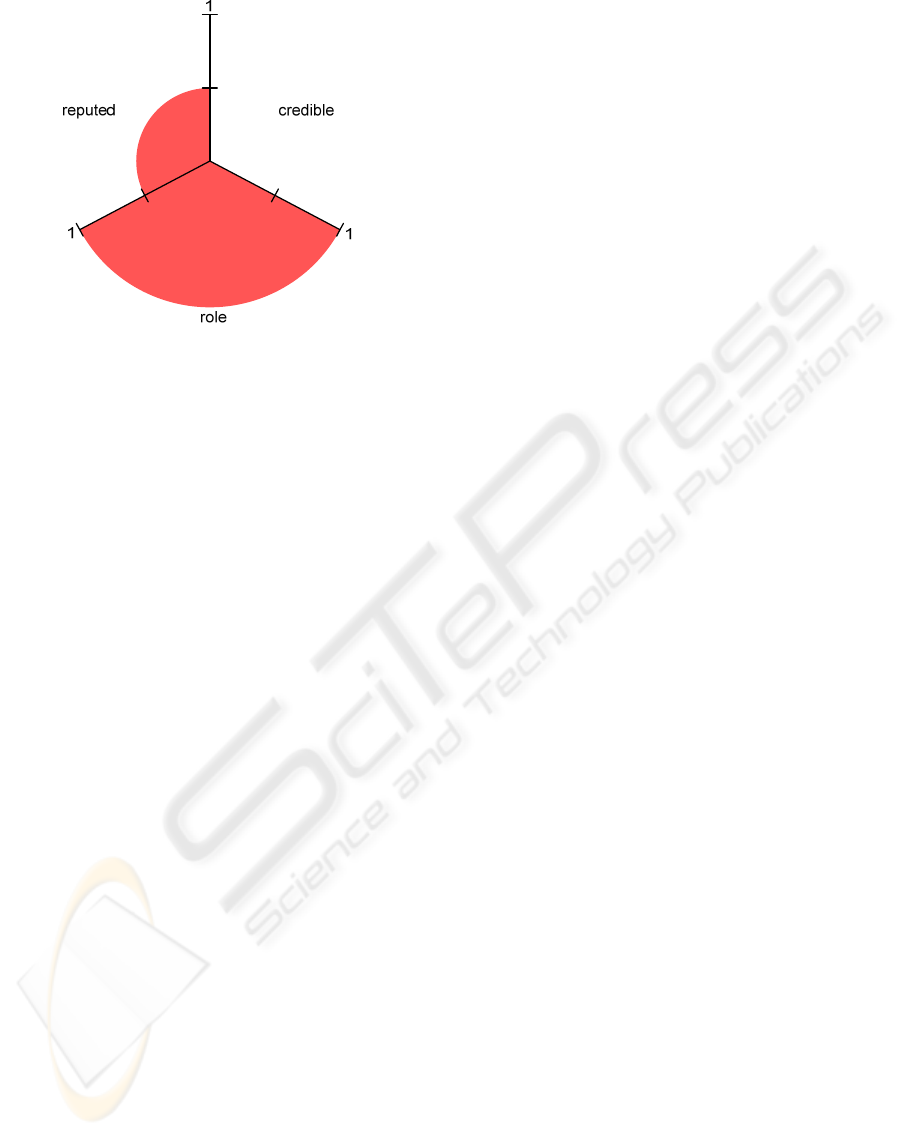
Figure 5: A measure of quality of knowledge about

participant Ricardo.

4 CONCLUSIONS

Our drive had in mind to measure (quantify) the

quality of knowledge of a logic theory or program

that makes a VirtualECare System (or Environment).

We began with an Extended Logic Programming

language to represent incomplete and uncertain

knowledge in the context of the VirtualECare

GDSS. It was also shown that negation-by-failure

combined with strong negation and predicate

circumscription, in a logic program, it is a possible

foundation for uncertain reasoning.

On the other hand, and starting with the

unknown truth value referred to in the extension of

the demo predicate, above, we elaborate on a model

of quantitative computation of the quality of

information presented in a logic program or theory,

in terms of a Multi-valued Extended Logic

Programming language. This makes the unknown

truth value to take truth values on the

interval

][

1..0 that fulfils our goal of measuring the

Quality of Knowledge in a Group Decision Support

System for Digital Homecare.

REFERENCES

Analide, C. et al., 2006, Quality of Knowledge in Virtual

Entities, in Encyclopedia of Communities of Practice

in Information and Knowledge Management. Elayne

Coakes and Stev Clarke (Eds).

Brito, L., P. Novais and J. Neves, 2003, The logic behind

negotiation: from pre-argument reasoning to

argument-based negotiaion, in Intelligent Agent

Software Engineering, V. Plekhanova (Ed), Idea

Group Piblishing. p. 137-159.

Cervenka, R. and I. Trencansky, 2007, The Agent

Modeling Language - AML: Birkhäuser Verlag AG.

Conklin, J., 2001, Designing Organizational Memory:

Preserving Intellectual Assets in a Knowledge

Economy. [cited 15-04-2008]; Available from:

http://cognexus.org/dom.pdf.

Conklin, J., 2006, Dialogue Mapping: Building Shared

Understanding of Wicked Problems. Wiley.

Costa, R. et al., 2007, Intelligent Mixed Reality for the

Creation of Ambient Assisted Living. Progress in

Artificial Intelligence, J. Neves, M. Santos and J.

Machado (Eds). Vol. 4874. 2007, Lecture Notes in

Artificial Intelligence, Spinger.

Denecker, M. and A. Kakas, 2002, Abduction in logic

programming, in Computational Logic: Logic

Programming and Beyond, Essays in Honour of

Robert A. Kowalski, Part I, A. Kakas and F. Sadri,

Editors. Springer Verlag. p. 402-436.

Eysenbach, G., 2001. What is e-health? Journal of Medical

Internet Research, 3(2).

Gelfond, M. and V. Lifschitz, 1990, Logic Programs with

Classical Negation. in Proceedings of the International

Conference on Logic Programming..

Ginsberg, M. L., 1991, Readings in Nonmonotonic

Reasoning, Los Altos, Califórnia, EUA: Morgan

Kauffman Publishers, Inc.

Hustadt, U., 1991, Do we need the closed-world

assumption in knowledge representation? in Working

Notes of the KI'94 Workshop. Saarbrüken, Germany:

Baader, Buchheit, Jeusfeld, Nutt (Eds.).

Neves, J., 1984, A Logic Interpreter to Handle Time and

Negation in Logic Data Bases. in Proceedings of the

ACM'84, The Fifth Generation Challenge.

Parsons, S., 1996, Current approaches to handling

imperfect information in data andknowledge bases.

IEEE Transactions on Knowledge and Data

Engineering, 8(3): p. 353-372.

Power, D. J., 2007, A Brief History of Decision Support

Systems. DSSResources.COM, World Wide Web,

version 4.0. [cited 15-04-2008]; Available from:

http://DSSResources.COM/history/dsshistory.html.

Shafer, G., 1992, The Dempster-Shafer theory, in

Encyclopedia of Artificial Intelligence, Second

Edition, S.C. Shapiro (Ed), Wiley.

Way, E. C., 1991, Knowledge Representation and

Metaphor. Dordrecht, Holland: Kluwer Academic

Publishers.

ICAART 2009 - International Conference on Agents and Artificial Intelligence

106