WORD SEGMENTATION BASED ON HIDDEN MARKOV MODEL
USING MARKOV CHAIN MONTE CARLO METHOD
Takuya Fukuda and Takao Miura
Dept.of Elect. and Elect. Engineering, Hosei University, Kajinocho 3-7-2, Koganei, Tokyo, Japan
Keywords:
Word Segmentation, Hidden Markov Models, Markov Chain Monte Carlo (MCMC) method.
Abstract:
It is well-known that Japanese has no word boundary, so that we should think about how to separate each
sentence into words by means of morphological analysis or some other word segmentation analysis. It is said,
however, that the separation depends on domain specific rules. The author have proposed a sophisticated word
separation method based on Conditional Random Fields (CRF). Unfortunately we need a huge amount of test
corpus in application domains as well as computation time for learning. In this investigation, we propose a
new approach to obtain test corpus based on Markov Chain Monte Carlo (MCMC) method, by which we can
obtan efficient Markov model for segmentation.
1 MOTIVATION
Recently there have been a wide variety of research
activities targeted for Web page text processing with-
out any knowledge of format, tags and commands.
Among others, text mining puts an emphasis on the
problem how we should analyze various kinds of free
texts such as minutes of meetings, daily reports and
questionnaire.
When we examine plain text documents, we face
to an issue of word segmentation in Japanese, Chinese
or some other languages. This is because there is no
boundary between words, and thus how to discover
the boundaries in text or speech is of interest for prac-
tical reasons such as morphological analysis. There is
no common rule to put space or any other punctuation
in Japanese, and when processing the texts, we should
start with word segmentation. We should think about
this issue as a step of morphological analysis.
There have been many interesting approach to the
morphological approach. One is based on local rules
and statistics, thus the process is driven by means of
rule interpretation. This is quite successful but it is
hard to extract rules, to keep the rules consistent and
no common procedures to extract. Another approach
is based on explicit probabilistic models or stochastic
process models. Analyzingtexts statistically, we learn
how morphemes act, i.e., we extract common patterns
in a probabilistic way. Traditionally there have been
assume common situation for all purposes. Even if we
know domain-dependent situation, it is hard to find
any useful solution.
In this investigation, we propose an experimen-
tal approach for word segmentation in Japanese un-
der domain-dependent situation. We apply Hidden
Markov Model (HMM) to our issue. Here we need
training corpus to obtain the HMM model. The more
corpus we have, the better rules we get. Clearly it
takes much time to huge corpus. To overcome the is-
sue, Baum-Welch (EM) algorithm has been proposed.
But the results depend heavily on the corpus. Com-
pared to such conventional discussion, we propose
completely differentapproach to obtain HMM models
based on Markov Chain Monte Carlo (MCMC) tech-
nique. By generating random values which capture
similar distribution to the corpus, we can obtain huge
amount of training corpus and improve the results.
In section 2, we review morphological analysis to
Japanese, and in section 3, we discuss word segmen-
tation problem. In section 4 we review HMM and
MCMC approach in section 5. Section 6 contains the
model to apply MCMC to segmentation problem, and
section 7 contains experimental results. We conclude
our work in section 8.
123
Fukuda T. and Miura T. (2009).
WORD SEGMENTATION BASED ON HIDDEN MARKOV MODEL USING MARKOV CHAIN MONTE CARLO METHOD.
In Proceedings of the International Conference on Agents and Artificial Intelligence, pages 123-129
DOI: 10.5220/0001666501230129
Copyright
c
 SciTePress

2 MORPHOLOGICAL ANALYSIS
AND SEGMENTATION
Documents consist of mainly texts, figures and tables,
texts contain many sentences which are sequences of
words. A word means a character string separated
by space or punctuation, but the problem is not re-
ally simple: how can we think about compound words
such as ” U.S.A. ”, idioms (a group of words carrying
a different meaning when used together) or colloca-
tion (the way that some words occur regularly when
other words are used) such as ” not only...but
also ”. A sentence in natural languages consists of
morphemes. A morpheme is a unit of strings carrying
minimal meaning. Each sentence can be decomposed
into a sequence of morphemes in a form of token (sin-
gle word), inflection (stemming) and part-of-speech
(POS) as noun and verb. The process is called mor-
phological analysis. In this work, by morpheme, we
mean a pair of token and part-of-speech attributes.
In morphological analysis, we have dictionary
which talks about relationship among morphemes,
and grammatical knowledge about morphemes. We
divide sentences into word segments, and examine
their role (and meaning) as well as the structural re-
lationship. The morphological analysis is one the key
steps for syntax and semantic analysis.
We know the fact that, in English, a word de-
scribes grammatical roles such as case and plural-
ity by means of word order or inflection. The dif-
ference between ”John calls Mary” and ”Mary calls
John” corresponds to the two interpretation of who
calls whom over John and Mary. Such kind of lan-
guage is called inflectional language.
On the other hand, in some languages as Japanese
and Chinese, grammatical relationship can be de-
scribed by means of postpositional particles, and such
kind of languages is called agglutinative language.
For example, ”I”, ”My” and ”Me” correspond to ”
”, ” ”, ” ” respectively where ”” means the first per-
sonal pronoun. The differences are 3 postpositional
particles ””, ”” and ”” which define subjective, pos-
sessive and objective respectively. As for John and
Mary, the two sentences ”W ł AŁ[ ”, ”W AŁ[ ł ” cor-
respond to the two sentences ”John calls Mary” and
”Mary calls John” where the positions of ”W”(John),
”AŁ[”(Mary) and ””(call) are exactly same but the
difference of postpositional particles. There is an-
other problem, there is no boundary between words
in Japanese. Basically, if we get words and rele-
vant postpositional particles, we could specify seg-
mentation. Morphological analysis examines roles of
words and determines which parts should be attached
to which words. In our case, we put tags between
words such as ”/Wł/AŁ[/” and ”/W/AŁ[ł/”. In agglu-
tinative languages, word segmentation plays essential
role on syntax and semantic analysis.
It is also important for the analysis step to examine
compound words. For example, we can decompose
”Łw” (University Education) into ”Łw”(University)
and ””(Education) but not ”Łw” (University Student)
into ”Łw” and ””. Such segmentation rules depend of-
ten on application domains. In this investigation, we
propose an experimental and efficient approach of do-
main dependent word segmentation base don stochas-
tic process. We apply n-gram model to Japanese,
examine relationship between morphemes by Hidden
Markov Model (HMM) for the word segmentation.
3 SEGMENTING WORDS
In a case of inflectional languages, there is no sharp
distinction between word segmentation and part-of-
speech (POS) tagging, and we can apply similar tech-
niques to analyze and examine sentences. There
have been two major approaches proposed so far,
rule-based tagging and probability-based tagging. In
the former, we extract characteristic patterns between
words or POS tags and between some more ones be-
fore/after the words of interests. Then we put them
into a form of rules. For example, we may have a rule
”this is not a verb if the preceding word is a deter-
miner”. By using well-structured rule tables, we can
get rather excellent results. The problems arise, how
we can extract useful, global, consistent and efficient
rules ? The process is not trivial and hand-coded, thus
we take much time yet not reliable.
On the other hand, in probability-based tagging,
we apply some of probabilistic approach (such as
naive Bayesian classification) and stochastic pro-
cess approach to tagging. A Hidden Markov Model
(HMM) is one of the typical examples where tags are
considered as states and words as observation sym-
bols. Given word sequences (sentences), we guess
tag sequences by means of Maximal Likelihood Esti-
mation (MLE) under a simple Markov Model among
states.
These investigation are also really useful for ag-
glutinative languages such as Japanese since we need
POS tagging. However, given sentences in the lan-
guages, we need word segmentation techniques dif-
ferent from POS tagging: we should examine word
boundaries to make every word consistent by using
postpositional particles. This is not easy to detect the
boundaries, and some approach such as ”ChaSen” has
been proposed based on HMM.
As for compound words in morphological anal-
ICAART 2009 - International Conference on Agents and Artificial Intelligence
124

ysis, there might be no common rule in both kinds
of languages. For instance, ”c‘” (Narita Airport) is
a compound word (”c” for Narita, ”‘” for Airport)
and considered as one word in usual dictionaries. On
the other hand, ”‘” (Miyazaki Airport) is not and we
should have two words ”” (Miyazaki) and ”‘” (Air-
port). We see similar situation in English. ”Ballpark”
describes one concept that means a park for base-
ball playing, contained in a dictionary as one word.
However, ”Amusement park” consists of two words
”amusement” and ”park”, contained not as one word
but as a derivative of ”Amusement”.
We take a stochastic approach for segmentation.
Our idea is that we extract some knowledge from
training data and capture them in probability distri-
bution, then we must have much excellent quality of
word segmentation.
4 A HIDDEN MORKOV MODEL
In this investigation, we discuss a Hidden Markov
Model (HMM) which is an efficient stochastic vehi-
cle. HMM is a probabilistic automata based on a
simple Markov model where a label corresponds to a
state and an observationsymbol to an output at a state.
Both state transition and output symbols are described
in a probabilistic manner. Formally we say HMM has
a model M = (Q, O, a, b, π) where Q, O mean a finite
set of states and a finite set of output symbols respec-
tively. A transition from a state i to j arises with prob-
ability a
ij
but it doesn’t depend on any other states.
This property is called simple-Markov. Generating an
output symbol o
t
∈ O depends only on a current state i
with probability b
i
(o
t
) where
∑
t
b
i
(o
t
) = 1. An initial
state happens to be i with probability π(i).
In HMM, we can observe an (output) sequence
but we don’t know on which states we are stand-
ing and how state transition arises according to a
simple Markov model. This is why we say hid-
den. Given a model M and an observation sequence
X =< x
1
, ..., x
i−1
, x
i
, x
i+1
, ..., x
n
>, we like to guess
label sequence Y =< y
0
, ..., y
i−1
, y
i
, y
i+1
, ..., y
n
> that
is most likely to generate an output sequence X in a
sense of probability. For this purpose, there have been
proposed some techniques of dynamic programming
such as Viterbi algorithm.
Clearly it is hard to determine definitely {a
ij
},
{b
i
(o
t
)} and the initial probability π in a model of
HMM. This problem is called a model calculation of
HMM. Usually we do that by means of some machine
learning techniques.
One of the typical approach is supervised learn-
ing. In this approach, we assume training data in ad-
vance to calculate the model, but the data should be
correctly classified by hands since we should extract
typical patterns them by examining them. And, an-
other approach is called unsupervised learning. As-
sume we can’t get training data but a mountain of un-
classified data except a few. Once we obtain strong
similarity between the classified data and unclassified
data (such as high correlation), we could extend the
training data in a framework of Expectation Maxi-
mization (EM) approach.
One of the well-known approach in unsupervised
learning is a Baum-Welch algorithm. The algorithm
has been proposed based on Expectation Maximiza-
tion (EM) approach. That is, the algorithm adjusts
the parametersmany times to maximize the likelihood
for the generation of the output symbols given as un-
supervised data. The process goes just same as EM
calculation, i.e., we calculate the expect value of the
transition probability and the output probability, then
we maximize them. We do that until few change hap-
pens. Baum-Welch approach is easier to apply for
model calculation even if small amount of training
data is available. However it often provides us with
tremendously imprecise results because the approach
depends only on initial values.
On the other hand, we can estimate the model di-
rectly under supervised learning. We assume enough
training data in advance to calculate the model and
examine sequences of both states and output symbols.
Then we count their frequencies and consider the rela-
tive values as the probabilities. Formally, we consider
the relative frequency
1
of transition from i to j as a
ij
,
the relative frequency of the initial state i as π(i), and
the relative frequency of output symbol o
t
at a state i
as b
i
(o
t
). The model reflects the situation in training
data correctly and we could obtain excellent results.
However, we should have enough amount of training
data to estimate all the possibilities in HMM which is
hard, time-consuming and costly.
We take the direct calculation approach to obtain
precise models. But how about training data ? This is
the true goal of this investigation. We generate train-
ing data automatically enough to obtain reliable mod-
els.
5 MARKOV CHAIN MONTE
CARLO METHOD
A Monte Carlo Method is a general framework to gen-
erate random numbers. Random numbers based on
1
Precisely we say a
ij
= (frequency of transition from i
to j)/(all the frequencies of transition from i).
WORD SEGMENTATION BASED ON HIDDEN MARKOV MODEL USING MARKOV CHAIN MONTE CARLO
METHOD
125

uniform distribution or normal gaussian distribution
can be generated through many intrinsic functions of
software, but it is not easy to obtain random numbers
according to any probability density function. Gen-
erally we can apply a sophisticated algorithm of re-
jection sampling. However, it is not common to ob-
tain these functions over state space A in advance.
If we are given non-parametric information such as
frequency and empirical knowledge, we can’t utilize
general sampling algorithms.
A notion of Markov Chain Monte Carlo method
(MCMC) is a general framework by which we can
generate random numbers approximatelyaccording to
a given distribution in any form. Generally MCMC is
not really efficient so that they have been proposed
several algorithms of Gibbs Sampler which are effi-
cient and easy to implement.
Let us go inside the detail. Given a state space A=
{1, .., N}, a sequence of random variables X
1
, ..., X
n
of length n over A and a sequence of states s
1
...s
n
where s
i
∈ A, we can think about a probability P(X
1
=
s
1
, .., X
n
= s
n
). We say the probability is stationary if
we can determine the value functionally on state se-
quences. Let us note that we can’t always determine
the probability even if we get exactly same s
1
...s
n
.
Assume we have stationary probability distribu-
tion. Given an initial state s
0
and a sequence start-
ing with s
0
, say, s
0
s
1
...s
n
, we say the sequence has
Markov Chain property if P(X
0
= s
0
, X
1
= s
1
, .., X
n
=
s
n
) = P(X
n−1
= s
n−1
, X
n
= s
n
), that is, a probability
X
n
= s
n
under X
0
= s
0
, X
1
= s
1
, ..., and X
n−1
= s
n−1
depends only on the situation of X
n−1
= s
n−1
. In this
case, when we have a transition probability p
ij
from a
state i to j, we can say P(X
n
|X
0
= s
0
) = p
n
P(X
0
= s
0
).
Moreover, under some condition
2
, we can prove the
existence of invariant distribution lim
n→∞
P(X
n
).
MCMC assumes Markov Chain property for state
transition, and generates random numbers approxi-
mately along the invariant distribution by using non-
parametric information. To do that, we generate X
n
from X
n−1
recursively until we get to stationary situa-
tion, and then we obtain desired sets of random num-
bers.
When generating random numbers, very often
we like to generate vectors x
k
= (x
(k)
1
, .., x
(k)
m
) over
{1, .., N}, but it takes much time and memory to ap-
ply MCMC in a straightforward manner. To gen-
erate vectors efficiently, we generate each compo-
nent x
(k+1)
i
in an one-by-one manner. Gibbs Sam-
pler is an algorithm to utilize a conditional probability
P(x
(k)
i
|x
(k+1)
1
, .., x
(k+1)
i−1
, x
(k)
i+1
, .., x
(k)
m
) in a serial manner.
2
This is called Ergodic conditions, though we skip this
issue.
It is possible to show that the result state transitions
satisfy Markov Chain property if state transitions at
vector level satisfy Markov Chain property.
In this experiment, we generate a random number
s by using Gibbs Sampler. Given a random variable
x
k
= (x
(k)
1
, .., x
(k)
m
), a set of initial (observation) data Y
with its distribution function ρ, we generate random
numbers as follows:
1. Generate m randomly between the minimum and
the maximum given.
2. Generate initial values appropriately:
(x
(0)
1
, x
(0)
2
, ..., x
(0)
m
)
3. Generate x
(1)
1
randomly accoding to the distribu-
tion ρ(x
1
|x
(0)
2
, ..., x
(0)
m
).
4. Generate x
(1)
2
randomly according to the distribu-
tion ρ(x
2
|x
(1)
1
, x
(0)
3
, ..., x
(0)
m
).
5. We repeat this process and we obtain x
(k)
.
Let us note x
(k)
comes to lim
k→∞
x
(k)
which is a sam-
ple according to the invariant distribution ρ(s|Y). We
should repeat the process until we get to stationary
situation, but practically we can assume k is finite.
6 WORD SEGMENTATION
BASED ON MCMC
In this section, let us discuss how to generate training
data for word segmentation based on MCMC. Since
we calculate a model for a HMM directly by count-
ing frequencies along with state transitions and output
generation in HMM, we should generate huge amount
of training data based on MCMC.
As an initial set of observation data, we are given
a set of sentences in Japanese. We translate each sen-
tence by hand into a sequence of morphemes, each
morpheme consists of a word and a tag B (means Be-
gin) or I (means Intermediate). We apply ”Chasen”
to obtain sequences of words, and then we examine
frequencies of the morphemes. For example, let us
examine a sentence: ”” (I see a dog) We apply mor-
phological analysis to this sentence and we obtain a
sequence:
””(”I”, pronoun), ””(postpositional particle
for subjective), ””(”dog”, noun), ””(postposi-
tional particle for objective), ””(”see”, verb)
Then we apply word segmentation with B and I by
hand:
”(B)”, ”(I)”, ”(B)” ”(I)”, ”(B)”
ICAART 2009 - International Conference on Agents and Artificial Intelligence
126

This is equivalent to the sequence
3
below:
/ / //
Now we translate each morpheme into a num-
ber in an one-by-one manner and count the frequen-
cies. This is the set of initial observation data Y. We
generate the distribution ρ from Y. Now we start
with Gibbs Sampler algorithm. Let m be a number
which is randomly generated between the minimum
and maximum lengths of sentences in the initial set.
Given a number m of words in each sentence and a
set of m initial values (all these values are generated
randomly), we generate a ”sentence” (a sequence of
words) s = (s
1
, .., s
m
) according to ρ. We repeat this
step as many as we need.
Let us note that there exists no special meaning
in a ”sentence” generated by Gibbs Sampler. How-
ever, Y contains word information (such as frequen-
cies) and co-occurrence information over any consec-
utive words (such as collocation). Thus any sentences
generated might contain partially consistent informa-
tion.
For example, as described later, we examine
Patent Information of Instrument in Japan for exper-
iments. Applying our process, we get plausible sen-
tences in Instrument field like:
/ /y / / / / /
(/in tank/y is/this/to axis/wind-
tunnel/processed/)
We can calculate a model of HMM by using generated
sentences.
7 EXPERIMENTS
In this experiment, let us show the effectiveness of
our approach for word segmentation. As initial train-
ing data, we examine agriculture-related morphemes
and instrument-related morphemes from Patent infor-
mation (1998 and 1999) in Japan
4
.
7.1 Preliminaries
In this experiment, we examine agriculture-related
859 morphemes (289 distinct words) and instrument-
related 1030 morphemes (229 distinct words) from
Patent information (1998 and 1999) in Japan
5
. Then
we have generated 8579 random numbers and 7240
random numbers for agriculture field and instrument
3
This means a correct sequence in Japanese: ”I”, ”dog”,
”see”
4
We have examined NTCIR-3 PATENT information.
5
We have examined NTCIR-3 PATENT information.
field respectively. As test data, we have examined
other sets of patent information (agriculture-related
3886 morphemes and instrument-related 3569 mor-
phemes) from Patent information (1998 and 1999).
We have examined both training and test data by
hands. We also examine morphological analysis by
Chasen.
Here we examine 3 kinds of experiments to see
how useful MCMC plays. We generate several
numbers of morphemes and examine the results by
MCMC to see how well word segmentation works.
Note that we generate training data from small num-
ber of initial data. Then we compare our results with
the ones of Baum Welch algorithm. Also we examine
the results by Conditional Random Fields (CRF).
In our experiment, we evaluate the results to word
segmentation based on HMM by means of correctness
ratio defined as follows:
The Number of Correct Morphemes
The Number of Morphemes
× 100( % )
7.2 Results
Let us show the segmentation results by HMM with
several numbers of training data. Note we calculate
the HMM model by using frequency of training data
which is generated by Gibbs Sampler.
Let us illustrate the results of segmentation in agri-
culture data in a table 1. As shown, we get the max-
imum ratio 74.70 % with 6000 morphemes. Also we
get the improvement of 3.68 % between 5000 and 6000
morphemes. Also we show the results in instrument
data in a table 2 where the ratio keeps constant.
Table 1: Ratios in Agriculture Data.
Morphemes MCMC ( % ) BW ( % )
997 71.23 49.69
2016 71.08 48.79
3019 70.84 48.81
4002 70.51 50.64
5007 71.02 50.15
6004 74.70 50.59
7022 74.60 50.49
Let us look closer at incorrectly segmented data
in agriculture appeared in 6000 morphemes but not
5000 morphemes. There exist 254 occurrences at
5000 morphemes and 206 occurrences at 6000 mor-
phemes, and we see technical terms such as housing
and hole in agriculture. On the other hand, there arises
no occurrences in incorrectly segmented data.
We also show the results by Baum-Welch algo-
rithm in tables 1 and 2. In agriculture case, we get
the best result 74.70 % of MCMC approach at 6000
WORD SEGMENTATION BASED ON HIDDEN MARKOV MODEL USING MARKOV CHAIN MONTE CARLO
METHOD
127

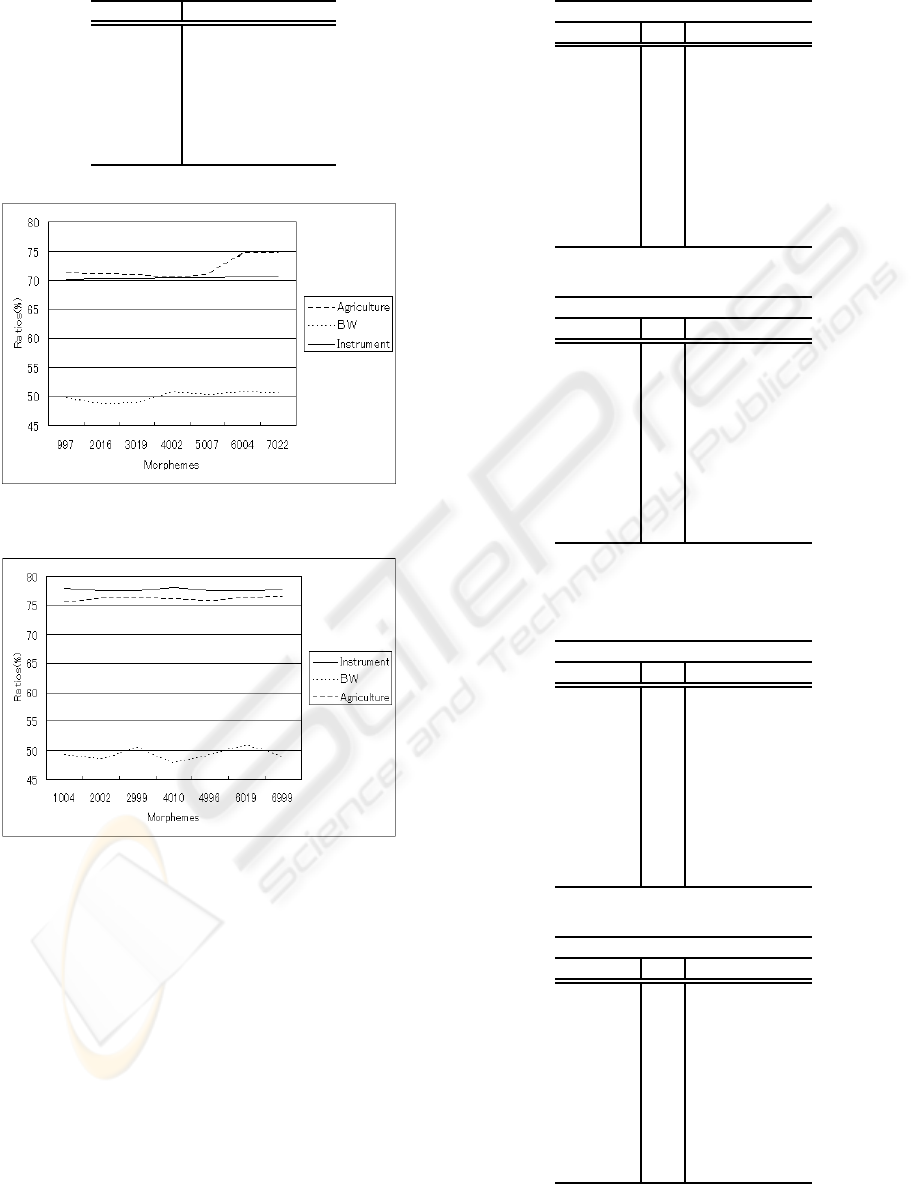
Table 2: Ratios in Instrument Data.
Morphemes MCMC ( % ) BW ( % )
1004 77.95 49.23
2002 77.58 48.42
2999 77.50 50.43
4010 78.17 47.69
4996 77.58 49.17
6019 77.56 50.83
6999 77.61 48.98
Figure 1: Ratios in Agriculture Data.
Figure 2: Ratios in Instrument Data.
morphemes while 50.64 % of Baum Welch approach
at 4000 morphemes, 24.04 % better. Similarly in in-
strument case, we get 78.17 % of MCMC at 4000 mor-
phemes and 50.83 % of BW at 6000 morphemes, 27.34
% better.
Let us see the results in more detail. We show the
morphemes which are incorrectly segmented by BW
approach. Generally we can say postpositional par-
ticles such as ”” and ”” appear though they can’t be
there. On the other hand, we see nouns in MCMC
approach which depend on application domain and
training data.
Finally let us compare the results with CRF.
Table 3: Incorrect Data in Agriculture.
MCMC
Morpheme Tag Incorrect Answers
vf B 62
) B 41
, B 37
B B 35
B 32
B 31
B 30
B 26
B 25
B 19
Baum-Welch
Morpheme Tag Incorrect Answers
A B 190
B 91
vf B 73
j B 66
B 59
B B 55
z B 42
y I 41
ł B 41
bh I 40
Table 4: Incorrect Data in Instrument
MCMC
Morpheme Tag Incorrect Answers
u B 56
x I 33
q[[ I 31
w B 26
B 19
a B 18
B 17
‘ I 13
M I 11
tM I 11
Baum-Welch
Morpheme Tag Incorrect Answers
B 145
B 84
I 59
q[[ I 47
x I 44
I 42
B B 34
z B 32
tM I 29
ł B 29
ICAART 2009 - International Conference on Agents and Artificial Intelligence
128

In tables 5 and 6, we show the comparison re-
sults where CRF approach requires about 13000 mor-
phemes for training. In agriculture case, we get the
best result 74.70 % of MCMC approach at 6000 mor-
phemes, so 21.90 % worse. Similarly in instrument
case, we get 78.17 % of MCMC, 19.95 % worse.
Table 5: Comparison in Agriculture.
Approach Ratio ( % )
MCMC (6000) 74.70
CRF 96.60
Table 6: Comparison in Instrument.
Approach Ratio ( % )
MCMC (4000) 78.17
CRF 98.12
7.3 Discussion
Let us discuss what our results mean. We have exam-
ined the segmentation results and shown that the re-
sult increases at 6000 morphemes in agriculture data,
although there exists no sharp distinction in instru-
ment data. This means we need enough amount of
data to obtain reasonable results although they depend
on application domains. We can say that MCMC is
useful to word segmentation since we have generated
enough amount of training data (remember we have
about 1000 morphemes in advance).
Compared to Baum Welch approach, we have ob-
tained the better results, say more than 25 % better,
whichever the number of training data we have. We
can apply word segmentation correctly in MCMC ap-
proach, since we put I tag correctly to postpositional
particles while we can do that hardly in BW approach.
CRF approach is excellent, say more than 20 %
better in our experiments. But we need 13000 mor-
phemes in advance for this purpose, while we have
assumed about 1000 morphemesin MCMC approach.
Also Gibbs Sampler is much efficient compared to
CRF.
8 CONCLUSIONS
In this investigation, we have proposed word segmen-
tation based on HMM. More essentially we have dis-
cussed how to generate training data automatically
based on MCMC and we have shown the experimen-
tal results. Then we have shown superior results and
MCMC is really useful for this purpose. In this work,
we have just discussed MCMC approach for HMM,
but we can generalize the techniques to other stochas-
tic frameworks. Then we could have enhanced ideas
depending on new kinds of POS tags.
REFERENCES
Abney, S.: Part of Speech Tagging and Partial Parsing,
In Corpus-Based Methods in Language and Speech,
Kluwer Academic Publishers, 1996
Fukuda, T., Izumi, M. and Miura, T.: Word Segmenta-
tion using Domain Knowledge Based On Conditional
Random Fields, proc. Tools with Artificial Intelligence
(ICTAI), pp.436-439, 2007
Gelfond, A.E. and Smith, A.F.M.: Sampling-based Ap-
proaches to Calculating Marginal Densities, J. of the
American Stat. Assoc. Vol.85, pp.398-409, 1990
Igarashi, H. and Takaoka, Y. Japanese into Braille Trans-
lating for the Internet with ChaSen proc.18th JCMI,
2K6-2, 1998
Kita, K.: Probabilistic Language Model, Univ. of Tokyo
Press, 1999 (in Japanese)
Kudo, T., Yamamoto, K. and Matsumoto, Y.: Applying
conditional random Fields to Japanese morphological
analysis, proc. EMNLP, 2004
Mitchell, T.: Machine Learning, McGraw Hill Companies,
1997
Ohmori, Y.: Recent Trends in Markov Chain Monte Carlo
Methods, J.of the Japan. Stat.Assoc. , Vol.31, pp.305-
344, 2001 (in Japanese)
WORD SEGMENTATION BASED ON HIDDEN MARKOV MODEL USING MARKOV CHAIN MONTE CARLO
METHOD
129