THE MASKLE: AUTOMATIC WEIGHTING

FOR FACIAL ANIMATION

An Automated Approach the Problem of Facial Weighting for Animation

Alun Evans, Marco Romeo, Marcelo Dematei and Josep Blat

Barcelona Media – Centre d’Innovació / Universitat Pompeu Fabra, Av. Diagonal 177, planta 9, 08018 Barcelona, Spain

Keywords: Facial animation, Automated animation, Weighting.

Abstract: Facial animation of 3D characters is frequently a time-consuming and repetitive process that involves either

skeleton-rigging or pose-setting for morph targets. A major issue of concern is the necessity to repeat

similar tasks for different models, re-creating the same animation system for several faces. Thus there is a

need for reusable methods and tools that allow the introduction of automation into these processes. In this

paper we present such a method to assist in the process of facial rigging: the Maskle. Based upon the

standard bone-weight linear skinning animation technique, the desired distribution of vertex-movement

weights for facial animation is pre-programmed into a low-resolution, generic facial mask. This mask, or

‘Maskle’, is then semi-automatically overlaid onto a newly created face model, before the animation-weight

distribution is automatically transferred from the Maskle to the model. The result is a weight-painted model,

created semi-automatically, and available for the artist to use for animation. We present results comparing

Maskle-weighted faces to those weighted manually by an artist, which were treated as the gold standard.

The results show that the Maskle is capable of automatically weight-painting a face to within 1.58% of a

manually weighted face, with a maximum error of 3.82%. Comparison with standard professional automatic

weighting algorithms shows that the Maskle is over three times more accurate.

1 INTRODUCTION

The goal of facial animation for 3D models is to

enable the representation of emotions and

expressions in a plausible manner. Since pioneering

work in the field was first published over 25 years

ago (Parke, 1982), a large of amount of research has

been carried out on the development of

computational models of the human face. The

ultimate goal for this research is a system that 1)

creates convincing animation, 2) operates in real

time, 3) is automated as much as possible and 4)

adapts easily to individual faces. While there has

been significant progress towards solving each of

these four matters individually, there has been

relatively little progress in developing techniques

that succeed in solving all four of the problems

simultaneously. It is with this goal in mind that we

present the first results of a novel method for

automatic bone-weight facial rigging, called the

Maskle. The motivation for the development of the

Maskle has two sources. The first is the amount of

time it can take an experienced artist to create a

simple animation on a 3D face model, even using a

powerful tool such as Autodesk’s Maya or 3DS

Max. The second is the multimedia industry’s

increasing need for reusable tools to assist in

production work, reflected by current research being

carried out by several EU-funded projects, for

example SALERO (SALERO, 2006). The concept

of the Maskle is a result of direct contact of

academic researchers with multimedia production

companies, and the results of the research are being

directly funnelled into the professional sector.

The main contribution of this paper is in the area

of facial animation, specifically towards automation

of the facial animation process. We show the results

of our initial tests which are designed to ascertain

whether the Maskle is a viable concept for use

within a professional production. The results

obtained show a mean error of only 2.63%, and have

led to the Maskle system being used already by our

production partners.

233

Evans A., Romeo M., Dematei M. and Blat J.

THE MASKLE: AUTOMATIC WEIGHTING FOR FACIAL ANIMATION - An Automated Approach the Problem of Facial Weighting for Animation.

DOI: 10.5220/0001753602330240

In Proceedings of the Fourth International Conference on Computer Graphics Theory and Applications (VISIGRAPP 2009), page

ISBN: 978-989-8111-67-8

2 RELATED WORK

The techniques used for the rigging of 3D characters

to create convincing facial animation can be broadly

divided into two distinct areas. The first are those

that focus on mimicking the movement of the face

surface only, attempting only to replicate facial

poses using surface deformations (Guenter et al.,

1998; Kalra et al., 1992). The second are those that

model the anatomy of the face, attempting to

replicate the movement of bones and muscles within

a virtual framework (Lee et al., 1995; Platt and

Badler, 1981; Waters and Frisbie, 1995). Some of

the earliest work in facial animation represents this

split, with Parke’s work on the parameterisation of

faces balanced by Waters’ (Waters, 1987) attempt to

replicate facial movement by modelling the

movement of muscles. In the decades since this

pioneering work there has been considerable

research effort put into to generating realistic facial

animation, much of it reviewed in detail by Noh and

Neumann (1998) and Ersotelos (2008).

Of particular relevance are Lee et al.’s (1995)

efforts at digitising facial geometries and

automatically animating them through the dynamic

simulation of facial tissues and muscles. Their

approach was to construct functional models of the

heads of human subjects from laser-scanned range

and reflectance data. These models were then

extended with contractile muscles embedded within

a dynamic skin model. The result was automatic

animation of a human face from a scanned subject.

Noh and Neumann (Noh and Neumann, 2001)

made considerable advances within the field of

automatic character animation with their work on the

cloning of expressions. Their technique was one of

the first to directly address the problem of reusing

existing animations, and transferring them to newly

created virtual characters. After letting users select a

set of points of the surface of a model, their method

was able to transfer vertex motion vectors from a

source character to a target character, with the aid of

an automated heuristic correspondence search.

Orvalho et al. (Orvalho et al., 2006) extend this

concept by attempting to adapt a generic facial rig to

different facial models. The technique required

considerable labelling effort yet was able to find

corresponding points between source and target

faces. This point matching was then used as a basis

for the transfer of a complex, muscle-based facial rig

system, to enable the target face to replicate the

expressions provided by the base rig. Although this

technique is of some interest, the authors do no

present quantitative results, and only a few

qualitative images to prove the validity of their

method.

Despite these efforts, there is still substantial gap

in the state of the art that remains to be filled before

we reach a facial modelling system that fulfils all

four points mentioned above in section 1. In this

paper we present our efforts at addressing this gap,

with a highly automated system that is capable of

enabling artists to quickly create suitable facial

animation for a wide variety of face models.

3 THE MASKLE

3.1 Overview

The concept of the Maskle is to allow artists to

create a facial animation system once, yet be able to

re-apply it to as many characters as they desire. In

this sense, the keyword is that the system is

reusable. Unlike some of the related research

presented above, the goal of the system is not to

transfer an animation system from one face to

another; neither is it to automatically animate a face

based on a scan or photograph. Rather, it is designed

such that an artist can develop their own system of

facial animation and, once designed, quickly apply

this system to any number of characters that they

create.

The type of facial animation system that the

Maskle is based around is a standard bone-weight

system, where the deformation of the set of vertices

that form the skin of a model is controlled by the

movement of an underlying skeleton; the exact

movement of each vertex (proportional to the bones

of the skeleton) is represented by a set of numeric

proportions, or weights, assigned to each vertex. The

justification for basing our algorithm on a bone-

weight system, as opposed to other animation

systems such as blend shapes, is that the bone-

weight system can be abstracted to a number of

control points (representing the locations of the

bones); this abstraction facilitates the organisation of

weight-transfer algorithm presented below, and

allows rapid testing to ensure the results are

satisfactory.

Once an artist has created a character, bone-

weight animation of a face usually requires

extensive effort in accurately assigning, or painting,

the weights for each vertex and for each bone. This

can be done automatically, and many 3D design

packages such Autodesk Maya and 3DS Max have

such functionality, frequently based around using

envelope systems (Autodesk, 2007). However,

GRAPP 2009 - International Conference on Computer Graphics Theory and Applications

234

despite being generally successful at automatically

painting body areas where the skin can be tightly

bound to the bone (such as the arms or legs), these

existing systems are less suitable for facial rigs,

where the ‘bones’ of the face are rarely modelled on

the real-life bones of a skull. Thus, weight-painting a

newly designed character to fit an existing facial rig

becomes a labour intensive and time consuming

process, as there is little existing automation that can

be used.

The Maskle system directly addresses this

problem by using a pre-painted, low resolution mask

to automatically weight-paint a newly created face.

The initial step is for an artist to create a facial rig,

(according to individual requirements) for the

Maskle itself. Given this rig, the overall process

occurs as follows. After the user has marked a total

of ten specific marker points around the areas of the

lips and the eyes, the structure of the Maskle is

loaded. This structure consists of a low-resolution

facial ‘mask’, designed so that it will be able to wrap

around areas of a 3D face that are commonly used

for animation. The Maskle is then adjusted semi-

automatically so that it shrinks around the shape of

the face; a collision detection algorithm detects

when the Maskle has contacted the face and prevents

its further movement. Once the Maskle has wrapped

around the face, ray-face collision algorithms find,

for each vertex of the face model, the nearest point

on the surface of the mask, which is then used to

calculate the animation weight for each vertex of the

face mesh. The Maskle can then be deleted, leaving

the face surface bound to the bone rig, ready for

animation.

The mesh used to represent the Maskle can vary

in terms of its actual structure. However, for the

work presented in this paper, the Maskle structure

consists of a 90-vertex, 82-face, symmetrical

triangle/quad mesh. While it is designed to cover the

areas surrounding the lips and eyebrows; the precise

details of topology and dimensions are less relevant

due to the changes that it undergoes during the

process of fitting it to a target face (as explained in

section 3.2 below). The techniques presented in

sections 3.2 and 3.3 were developed using C++ and

Maya Scripting Language (MEL) to create a plug-in

for Autodesk Maya, due to it being one of the most

popular 3D modelling packages available. It has also

been ported to Autodesk 3DS Max, and the design

of the system is such that it is would be

straightforward to transfer it to other modelling and

animation tools such as Blender, or proprietary

software. The facial models used for testing and

evaluation are triangle/quad vertex-face models,

consisting of between 757 and 6603 vertices. Each

facial model must have a small gap between the

upper and lower lips to ensure correct weighting in

these areas (see below).

3.2 Automatic Fitting

To ensure that the animation weights for each vertex

are transferred as accurately as possible, it is

important that the Maskle fits closely over the face

model. More importantly, it is vital that the

equivalent areas of the mask and face model are in

close proximity; for example, the upper lip of the

Maskle must be in close proximity to the upper lip

of the face model. Failure to ensure this proximity

frequently results in errors in the transferring of

weights, for example, the upper lip of the face model

acquiring the weights from the lower lip of the

mask.

3.2.1 Initial Placement

Due to the wide variety of facial shapes and sizes

that can exist, for each face it is necessary to pre-

programme the Maskle with some figures that relate

to the scale of the model in question. Thus, the

fitting of the Maskle to the face is initialised by the

user manually marking ten vertices of the face: two

at the lateral boundaries of the lips; four along the

central axis of the face, marking the highest and

lowest vertices of both the upper and lower lip, and

four marking the inner and outer lateral points of

both eyes. While it is unfortunate that the user

should have to manually mark locations, the number

is substantially less than that required by similar

techniques (Orvalho et al. 2006).

Figure 1: View of the Maskle system post-initialisation

step.

Once the vertices have been marked, the

respective distances between them are used to scale

the basic Maskle shape so that it has the same

THE MASKLE: AUTOMATIC WEIGHTING FOR FACIAL ANIMATION -

An Automated Approach the Problem of Facial Weighting for Animation

235

dimensions (e.g. the distance between nose and

mouth) as the face. The Maskle mesh is then loaded

and placed in front of the face model. It is almost

entirely flattened to a 2D plane, with only a ‘tongue’

extending into the mouth. This ‘tongue’ is present to

ensure that the Maskle will correctly cover the lips

of the face model; if it is not present the probability

of either lip being assigned the animation weight of

the other is much higher. The final placement of

Maskle is decided by the user, to ensure that the

‘tongue’ of the Maskle enters the mouth at the

correct angle. Figure 1 shows the position of Maskle

post-initialisation.

3.2.2 Automatic Shrinking

Following the initial placement, the Maskle

undergoes an automatic movement/shrinking

process which allows the shape of the Maskle mesh

to hug closely the shape of the target face mesh. The

basic system of movement is a curtailed version of

the dynamic force formulation for active surface

models (Sonka and Fitzpatrick, 2000). An iterative

process applies a combination of forces to each

vertex, the direction and magnitude of each force

contributing to the overall movement. This method

was preferred over direct correspondence techniques

as it allows the structure of the Maskle to change

dynamically as it is laid over the face model; also it

is very fast.

The location, x

, of each vertex, v

, moving

through time t can be calculated as

(t+1) = x

(t) + F

(t) (1)

The total force, F, applied to each vertex at each

iteration is dependent on two forces; α and β.

(t) = aα

(t) + bβ

(t) (2)

a and b are factors used to control the influence

of α and

β respectively. α

(t) is calculated according

to:

(t) = c

- x

(t) (3)

where c

is the average coordinate location of the set

of vertices adjacent to v

(i.e. the set of vertices that

are connected to v

by a single edge). β

(t) is

equivalent to the normalised vector representing the

initial (i.e. when t=0) direction of the ‘tongue’ of the

Maskle (as mentioned above in 3.2.1) and is

calculated using the relative locations of the relevant

vertices of the Maskle mesh. The effect of iteratively

applying equation (1) to the vertices of the Maskle is

that each vertex moves (in Euclidean space)

according to the direction and magnitude of the

resulting vector. Thus, the mesh moves towards the

face model (due to the influence of β) and wraps

around it (due to the influence of α). The termination

condition for the movement is partially applied when

the Maskle mesh collides with the face model mesh

(alternatively, the user may choose to manually

terminate the movement phase). Specifically, if a

Maskle triangle/quad collides with the face model,

the constituent vertices of the Maskle are flagged

and prevented from further movement. Once all the

vertices of the Maskle have been flagged, the

algorithm stops. Collision detection is carried out by

Moller’s triangle-triangle intersection test algorithm

(Moller, 1997), optimised by a standard axis-aligned

octree (Ericson, 2005), and run at each movement

iteration. Quad faces are split into two constituent

triangles for the purposes of collision detection.

Figure 2 shows an example of the result of the

completed movement.

Figure 2: Final position of the Maskle for weight transfer.

It is important to note that the results of the

automatic shrinking algorithm are dependent on the

accuracy of the initial placement (described above in

section 3.2.1). If the initial placement is incorrect,

the overall dimensions of the Maskle structure will

be incorrect, and the automatic shrinking algorithm

will not hug the face model correctly.

3.3 Weight Transfer

Now that the Maskle mesh has been placed adjacent

to the face model, its location can be used to recreate

an existing rig on the model (as mentioned in section

3.1 above, such a rig will have been already created

by the artist and applied to the Maskle). Firstly the

system of bones of the facial rig is re-created. Given

the location of a manually created ‘base’ bone, a

simple script recreates the bones of the rig, using the

GRAPP 2009 - International Conference on Computer Graphics Theory and Applications

236

locations of the vertices of the Maskle to ensure

correct placement. The exact form of this script will

depend on the number of bones that form part of the

facial rig which the Maskle is applying. The

animation weights for each vertex and for each bone

can now be set for the face model. For each vertex

of the face model, an infinite bi-directional ray is

projected along the axis of the Normal vector of the

model surface at that vertex. An intersection test

(Ericson, 2005) is carried out between this ray and

the faces of the Maskle. If successful, this test

defines an intersection point, p

, which lies on the

plane of a quad/triangle face of the Maskle. This

face is labelled f

. Recalling that the Maskle vertices

have been already weighted by the artist during the

creation of the original facial rig, the coordinates of

on the surface of the Maskle are then used to

interpolate the animation weights associated with the

constituent vertices of f

. The method used for this

interpolation is the Inverse Distance Weighting, or

“Shepard”, method, where the interpolated value is a

weighted average of the values of the surrounding

points (Amidror, 2002). The interpolated weight

values for p

are then assigned the vertex of the face

model from which p

was created. To increase

computational speed, the process is carried out for

only those vertices of the face model that lie within

the largest possible circumsphere that can be created

using the vertices of the Maskle mesh. The result is

that the weights for each bone are interpolated from

the vertices of the Maskle to the vertices of the face

model. The final step is to run a smoothing

algorithm (Autodesk, 2007) that ensures even

distribution of weights over the area of the face. The

artist is now free to animate the face as desired.

4 EVALUATION

An evaluation of the Maskle was carried out to

prove that the concept of the weight-transfer system

had validity. The difficulty in designing such a test

is increased due to the very nature of the work that

the Maskle is designed to facilitate i.e. animating a

face. Such work can be highly subjective, and it is

important to try and remove or negate any influences

that may introduce such subjectivity. For example,

the Maskle is designed to work with a variety of

facial rig designs, and any evaluation procedure

should be as independent as possible from these or

other variable elements that exist in the animation

pipeline.

To this extent we designed an evaluation

procedure that tests only the capability of the Maskle

to transfer the weights for the correct regions of the

face. An artist created a very simple, seven-bone

facial rig, and applied it manually to the Maskle and

to four different face models. We then commenced

the evaluation process by using the Maskle to

automatically transfer its associated rig to unrigged

copies of same four face models. The values

assigned to variables a and b in equation (1) were

deduced according to visual inspection of the

movement path of the Maskle mesh, and were set to

0.005 and 0.05 respectively. They were kept

constant for all tests. Such low values ensure slow

movement of the Maskle mesh and thus more

accurate collision detection.

The success of the Maskle weighting was

measured by comparing the animation weight

distribution of manually weighted face-model (the

gold standard) and the Maskle-weighted face model

(the test candidate). However, doing this for every

single vertex in the face model could have

introduced bias into the procedure. This is because

neither artist nor Maskle will have applied animation

weights to immovable facial features (e.g. the ear)

and so these vertices should not be allowed to bias

any mean comparison towards smaller error. Thus,

we isolated the set of vertices of the face model

whose Normal vector rays intersect with the Maskle

(as described in section 3.3) and label this set M,

where M = {m

}, i = 1, …, I. The difference

between the manually weighted set, M

Manual

and the

Maskle-weighted set M

Maskle

, for each of the seven

bones in the rig, can now be calculated thus:

mmabs

diff

Maskle

Manual

bone

∑

−

)(

where is the weight of the i

vertex of set

Manual

and is the weight of the i

vertex of

set M

Maskle

Manual

Maskle

The total average difference between M

Manual

and

Maskle

is then calculated by averaging diff

bone

over

each of the seven bones in the test rigs. As the goal

was to test the weight distribution (i.e. the spread of

weights for each joint across the mesh), the

differences between manual and automatic were

normalised according to the difference in maximum

weight spread.

As a comparison, an industry standard envelope-

based automatic skinning algorithm (Autodesk,

2007) was applied to the same four faces, and the

differences calculated in the same way (using the

same set of vertices). Figure 6 shows a table with the

THE MASKLE: AUTOMATIC WEIGHTING FOR FACIAL ANIMATION -

An Automated Approach the Problem of Facial Weighting for Animation

237

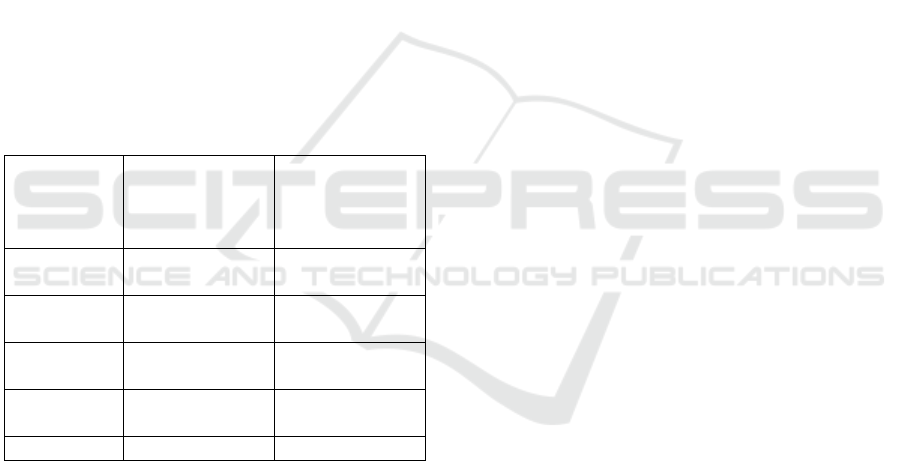
results as percentage of the total possible weight

(weight values range from 0 – 1, thus an average

weight difference of 0.5 means there is a gap

between the sets of 50% of the possible weight). The

face models have been labelled according to their

appearance.

Table 1 shows that the Maskle weighted face

achieves lower error rates in weighting all the test

models. When considering the mean figures, the

table shows that the Maskle is over three times more

accurate than the standard envelope algorithm.

Visual analysis of the results for each face shows an

even greater difference that the data in the table

illustrates, as the envelope based method deals very

poorly with the area of the lips, incorrectly

associating vertices of the upper lip to the bone of

the lower lip, and vice versa. The error can be seen

visually in Figure 4(c). Due to the nature of the

Maskle (specifically, the ‘tongue’ that divides the

upper and lower lips, this error is completely

removed.

Table 1: The mean differences between manually

weighted faces and automatically weighted faces. A

sample of each model is shown in Figures 4, 5 and 6.

Model Maskle

difference as %

of possible

weight

Envelope

difference

as % of

possible weight

Realistic

Human

1.58 8.43

Cartoon

Human

2.49 7.40

Cartoon

Devil

2.61 7.17

Venetian

Mask

3.82 11.92

Average 2.63 8.73

To illustrate this, Figure 3 consists of two graphs

that show the weight distribution profile for the

weights of the lower lip bone of one of the models

used in the study (the ‘Realistic Human’ model in

Table 1 and illustrated in Figure 4). Figure 3 (a)

shows a comparison between the manually weighted

face and the Maskle weighted face. The graph shows

that there the two sets of data overlap and that there

are very few vertices that are weighted in only one

of the sets. Figure 3 (b) shows a comparison

between the manually weighted face and the

envelope-algorithm weighted face. In this graph

there is less correlation between the datasets, and the

envelope algorithm has incorrectly weighted several

vertices which remain unweighted by the manual

operator. Further examples of animated faces

generated successfully using the Maskle can be seen

in Figures 4(b), 5 and 6.

5 DISCUSSION AND FUTURE

WORK

In this paper we have presented the concept of the

Maskle system and the results of a study on the

validity of using such a system. The novel

contribution is in the area of automation of facial

animation, with specific contribution in the

automated animation of areas of the face that are

time-consuming to animate manually, such as the

lips. The results show that the system used for this

study is capable of creating a facial rig that is, on

average, within 2.63% of being identical to that

created manually. This error rate is over three times

less than that obtained by carrying out the same tests

on a standard envelope-based weighting algorithm.

The Maskle is a novel idea of automatically

recreating a facial animation system on a variety of

face models, and addresses this issue in a way that is

different to work previously published; thus, it is

difficult to compare the obtained error rates with the

results published by other researchers. Perhaps the

most similar previous work is Orvalho et al.’s (2006)

efforts in transferring a facial animation system, yet

their work focuses strongly on transferring a rather

complex generic facial rig, and involves the user

manually marking 44 points landmark points. The

Maskle system is more flexible in that it can be used

with a variety of facial rigs, and only requires the

marking of ten landmark points. Unfortunately,

Orvalho et al. do not provide numerical results for

their technique, showing their results only in

graphical format, thus it is difficult to directly

compare the accuracy of the Maskle with their

results. Noh and Neumann (Noh and Neumann,

2001) presented statistics comparing the results of

the motion vectors for cloned expressions (i.e.

expression that are copied from a ‘source’ face to a

‘destination’ face). Again, this is difficult to

compare to the results in this paper, as the Maskle

does not attempt to directly transfer expressions,

rather it is directly transferring movement weights to

allow artists to animate as they desire.

Due to the low error rates, analysis of graphs of

the type shown in Figure 3, and visual analysis of

the face models, our interpretation of the results

obtained in the study is that the Maskle is a tool

that can greatly aid the process of creating facial

GRAPP 2009 - International Conference on Computer Graphics Theory and Applications

238

(a) (b)

Figure 3: Sample weight profiles for one bone of a manually-weighted face (blue line) and automatically weighted face (red

dashed line). Figure (a) shows the results for the Maskle, Figure (b) for the envelope algorithm. The envelope algorithm

shows a much greater level of noise and erroneous calculations.

(a) (b) (c)

Figure 4: Visual differences between Maskle-weighted and envelope-weighted faces, comparing a simple expression

created by moving the bones of the rig. (a) shows the unanimated face; (b) shows the expression applied to the Maskle-

weighted face; (c) shows the same expression applied to the envelope-weighted face.

animation for 3D characters. This being said, the

technique does have several limitations. The first is

that in its current state, the Maskle does not cover

certain areas of the face that are usually used in

animation e.g. the chin. The reason for this is that, in

practice, such areas are straightforward for even a

non-experienced artist to animate, and thus there is

little need for an automated tool to assist in this area.

By contrast the area around the lips is difficult and

time-consuming to animate, and it is this and other

similar areas in which the Maskle is of most use.

Nevertheless, in the interest of creating a more

comprehensive tool, our future work will involve

expanding the Maskle to cover other areas of the

face. A further limitation is in situations where the

face shape is very different to the structure of the

Maskle. The system works well with humanoid

faces, but has not yet been tested with animal,

fantasy, or highly abstract faces. There is also scope

for technical improvement by investigating different

methods of Maskle-face correspondence. While the

current method is adequate and fast, it does require

manual fine adjustment. Several other

correspondence techniques exist, and a study could

be carried out to see if using any of these improves

the system. Our immediate future work is to conduct

a more comprehensive evaluation study to measure

the impact of the use of the Maskle in real-life

animation situations, possibly recording the time that

it takes several artists to create a facial rig on several

characters, with and without the Maskle

Finally we also intend to combine the Maskle

with other facial animation work that is being

currently being conducted within our group, which

involves automatic creation of facial emotions

across a wide range of facial models. It is expected

that this further work will lead to a considerable

breakthrough in the field of automatic facial

animation, in which the Maskle system will play a

major role.

THE MASKLE: AUTOMATIC WEIGHTING FOR FACIAL ANIMATION -

An Automated Approach the Problem of Facial Weighting for Animation

239

(a) (b) (c)

Figure 5: Example of expressions successfully created using the Maskle on a cartoon character with pronounced features.

(a) is the unanimated face, (b) and (c) are expressions created after the Maskle has weighted the face.

Studio / University of Art and Design Helsinki 2008).

ACKNOWLEDGEMENTS

The authors would like to acknowledge the support

of the SALERO project http://www.salero.info.

REFERENCES

Amidror, I. 2002. Scattered data interpolation methods for

electronic imaging systems, a survey, Journal of

Electronic Imaging, 11, 2, 157-176.

Autodesk Maya Press. 2007. Learning Autodesk Maya

2008: The Modeling & Animation Handbook. Sybex.

Ericson,

C. 2005. Real-time Collision Detection. Morgan

Kaufmann.

Ersotelos, N. and Dong, F. 2008. Building highly realistic

facial modeling and animation: a survey, The Visual

Computer, 24, 13-30.

Guenter, B., Grimm, C., Wood, D., Malvar, H., and

Pighin, F. 1998. Making Faces, In Proceedings of

ACM SIGGRAPH 1998, 55-66.

Kalra, P., Mangili, A., Thalmann, N., and Thalmann, D.

1992. Simulation of Facial Muscle Actions Based on Rational

Free From Deformation. Eurographics, 11, 3, 59-69.

Lee, Y., Terzopoulos, D., and Waters, K. 1995. Realistic

Modeling for Facial Animation. In Proceedings of

ACM SIGGRAPH 1995, 55-62.

Lee, Y., Terzopoulos, D., and Waters, K. 2002. Realistic

Face Modelling for Animation. In Proceedings of

ACM SIGGRAPH 1995, 55-62.

Möller, T. 1997. A fast triangle-triangle intersection test,

Journal of Graphics Tools, 2, 2, 25-30.

Noh, J. and Neumann, U. 2001. Expression Cloning, In

Proceedings of ACM SIGGRAPH 2001, 277-288.

Noh, J. and Neumann, U. 1998. A survey of facial

modeling and animation techniques, USC Technical

Report.

Orvalho, V., Zacur, E., and Susin, A. 2006. Transferring a

Labeled Generic Rig to Animate Face Models, Lecture

Notes in Computer Science 4069, 223-233.

Parke, F. 1982. A parameterized Model for Facial

Animation, IEEE Computer Graphics and

Applications, 2, 9, 61-68.

Platt, S., and Badler, N. 1981. Animating Facial

Expressions. Computer Graphics, 15, 3, 245-252.

SALERO. 2006. http://www.salero.info/.

Sonka, M and Fitzpatrick, J. 2000. Handbook of Medical

Imaging, Vol. 2 Medical Image Processing and

Analysis. SPIE Press.

Waters, K. 1987. A Muscle Model for Animating Three-

Dimensional Facial Expression, Computer Graphics,

21, 4, 17-24.

Waters, K., and Frisbie, J. 1995. A coordinated Muscle

Model for Speech Animation, Graphics Interface,

163-170.

GRAPP 2009 - International Conference on Computer Graphics Theory and Applications

240