SEGMENTATION OF MULTISPECTRAL IMAGES USING

MATHEMATICAL MORPHOLOGY AND AUTOMATIC

CLASSIFICATION

Application to Microscopic Medical Images

Sarah Ghandour, Eric Gonneau and Guy Flouzat

LERISM, Toulouse University,118 Route de Narbonne, Toulouse, France

Keywords: Segmentation, Watershed Algorithm, Region Adjacency Graph, Mathematical Morphology, Generalized

Likelihood Ratio, Clustering, Hypercube Classification.

Abstract: In this paper, a new color segmentation scheme of microscopic color images is proposed. The approach

combines a region growing method and a clustering method. Each channel plane of the color images is

represented by a set of regions using a watershed algorithm. Those regions are represented and modeled by

a Region Adjacency Graph (RAG). A novel method is introduced to simplify the RAG by merging

candidate regions until the violation of a stopping aggregation criterion determined using a statistical

method which combines the generalized likelihood ratio (GLR) and the Bayesian information criterion

(BIC). From the resulting segmented and simplified images, the RGB image is computed. Structural

features as cells area, shape indicator and cells color are extracted using the simplified graph and then stored

in a database in order to elaborate meaningful queries. A regularization step based on the use of an

automatic classification will take place. Results show that our method that does not involve any a priori

knowledge is suitable for several types of cytology images.

1 INTRODUCTION

The image segmentation is an essential step of low-

level processing of imagery. It aims to split the

image into disjoint regions that are generally

homogenous in terms of color and texture. Various

algorithms and segmentation methods can be found

in the literature and can be divided into several

categories: clustering methods, edge-based

techniques, region growing process and

mathematical morphology. Please refer to (Lucchese

and Mitra, 2001) for more details about those state-

of-the-art techniques. Approaches combining some

of these methods were also proposed in (Lucchese

and Mitra, 2001) and (Lezoray and Lecluse, 2007).

In the context of automated analysis of medical

microscopic images, we are interested on studying

the color image segmentation in order to decompose

those images into meaningful entities.

Many of the existing medical images

segmentation methods involve a priori knowledge

as the desired number of classes and use many

parameters which are generally difficult to tune

(Lezoray, 2003). In this work, a novel unsupervised

method of microscopic color images segmentation is

presented in order to cure those weaknesses by

reducing the number of parameters. We propose to

combine different approaches of segmentation

towards this goal.

In this paper, we focused on studying the region

growing process based on morphological operations

applied to Region Adjacency Graph (RAG). The aim

of the region growing process is to simplify the

over-segmented images by merging the candidate

adjacent regions using morphological operations

until the violation of a stopping aggregation

criterion. This criterion is determined using the

combination of the Generalized Likelihood Ratio

(GLR) and the Bayesian Information Criterion (BIC)

used in the segmentation method proposed in (El-

Khoury et al., 2007).

This paper is organized as follows: in section 2,

we describe our morphological segmentation

process. In section 3 an original clustering method is

proposed. In section 4 we present the hypercube

classification. Then, results on cytological images

237

Ghandour S., Gonneau E. and Flouzat G. (2009).

SEGMENTATION OF MULTISPECTRAL IMAGES USING MATHEMATICAL MORPHOLOGY AND AUTOMATIC CLASSIFICATION - Application to

Microscopic Medical Images.

In Proceedings of the Fourth International Conference on Computer Vision Theory and Applications, pages 237-240

DOI: 10.5220/0001753702370240

 SciTePress

are shown in section 5. Conclusions and future

works are described in section 6.

2 MORPHOLOGICAL

SEGMENTATION

As the segmentation of color images may be time-

consuming and due to the numerous gray-scale

methods developed in the literature, we choose to

segment independently each RGB channel. First, the

images are represented and modeled by a set of

regions using a watershed algorithm (Lucchese and

Mitra, 2001). An important step in morphological

segmentation is to detect the edges of the objects in

the image to be segmented. Thus, we proposed to

use the color gradient image as input image for

watershed algorithm in order to provide the first set

of homogenous regions. Instead of using grayscale

gradient techniques to individual channels which

seems to be inadequate, we decide to apply a RGB

color gradient which provides more accurate

description of the image.

2.1 Color Gradient Watershed

Watershed algorithm constitutes an image

segmentation tool based on the mathematical

morphology (Lucchese and Mitra, 2001). This

process considers the image as a topographic surface

on which a flooding action starting from its minima

is applied. The basic idea of the watershed

construction is to create an influence zone for each

regional minima of the image. Generally, the

watershed transformation is applied on the gradient

of the image representing pixels altitudes.

Different gradients of color images were defined

in the literature (Hirata et al., 2000) to detect edges.

In our work, we used the supremum of the

morphological gradient computed on the red, green

and blue images. It is defined as follow:

sup R G B

BBBB

⎡⎤

∇=∨∇∇∇

⎣⎦

(1)

where

∇

is the classical Beucher gradient and B the

structuring element (Beucher and Lantuéjoul, 1979)

applied on every spectral channel and defined as the

arithmetic difference between dilation and erosion:

BBB

∇=δ−ε

(2)

This operator yields a grayscale image where each

point is the difference between the maximum and

the minimum gray levels of the image inside the

structuring element.

The resulting gradient image

sup

∇

is used as an

input image for the watershed algorithm. The

application of watershed algorithm provides an over-

segmented image represented by a set of disjoint

homogeneous regions

{}

12 n

RR,R,...,R= of any

sizes and shapes.

The proposed process will constitute a good

starting point to carry out the morphological process

on RAG.

2.2 Region Adjacency Graph

The Region Adjacency Graph (RAG) is an efficient

way to manipulate image information because it

provides a spatial adjacency view of the regions.

One way to represent a RAG consists of associating

a node

to each region

and an edge

each pair of adjacent regions

),(

. Two regions

are defined to be adjacent if they share the same

boundary. For more details about the RAG

construction, please refer to (Mestar et al., 2007).

To each node

are associated the relevant

attributes of the region it represents such as area,

perimeter, the mean gray level values of the region,

the length of the boundaries shared by adjacent

regions and a compactness factor of the regions.

2.2.1 Morphological Region Growing

Process on the RAG

In order to simplify the over-segmented regions and

obtain only the meaningful ones, we develop an

algorithm based on region growing process applied

on the RAG. In our case, the region growing process

starts with a region

already provided by the

watershed algorithm and then iteratively adds to

neighboring regions

(

)

VR which share some

spectral and spatial properties.

(

)

VR is defined as follow:

()

(

)

{

}

Ai j ij

VR R R,R,R A=∈ ∈

(3)

where A is the set of edges separating pairs of

adjacent regions.

VISAPP 2009 - International Conference on Computer Vision Theory and Applications

238

This region growing process on RAG is based on

applying morphological operations such as opening

and closing operations ((Mestar et al.,

2007),(Pesaresi and Benediktsson, 2001)) defined

respectively as follow:

iij

(RAG)(R ) Min(RAG(R ),Max(RAG(R )))γ=

(4)

iij

(RAG)(R ) Max(RAG(R ),Min(RAG(R )))ϕ=

(5)

where

{}

jAj i

RV(R)R=−

(6)

The geometrical action of the opening and

closing operations

(RAG)(R )γ

and

(RAG)(R )ϕ

respectively, consists of merging two candidate

adjacent regions

and

on the RAG in only one

area

()

RR ∪

if the aggregation criterion is

verified. This criterion is determined using a

clustering method.

3 CLUSTERING

To determine the aggregation criterion, we propose

to perform a thresholding using a statistical method

proposed in (El-Khoury et al., 2007)

.This approach

splits the histogram of the grayscale images into

several sections by computing automatically the

thresholds that separate the different representative

classes of pixels in the image without introducing

any a priori knowledge.

This method supposes that the probability

density function of each cluster is Gaussian and then

finds the most probable spectral points of change

that separated two consecutive clusters by using the

generalized likelihood ratio (GLR) and the Bayesian

information criterion (BIC). In our case, the

hypothesis test is defined as:

and

, two adjacent regions belong to

the same cluster.

and

, two adjacent regions belong to

different clusters separated by a point of change C.

The GLR is computed as followed:

)P(H

GLR

(7)

Once the points of change are detected a re-

adjustment step takes place in which GLR is applied

several times until stabilization. Finally the

definitive change detection step is processed using

BIC.

The clustering result is used to control the

morphological operations on the RAG. Therefore

two adjacent regions

and

that belong to the

same cluster will be merged on the RAG using the

opening and closing operations as described above.

The three segmented maps are fused together

giving the final segmented RGB image. A final stage

yields a segmentation refinement using the

hypercube classification.

4 HYPERCUBE

CLASSIFICATION

This method suppresses the isolated pixels and

filters the classes that contain less than 3 pixels that

are incorporated into the larger adjacent class with

which the minimum difference in color is verified. It

consists in detecting the valley on the gradient of the

histogram 1D of R, G and B on which an interval

[]

SSS Δ+

λλ

;

is defined for each of the three

components. The intersection of all intervals defines

classes. This process is shown in Figure 1.

Figure 1: Hypercube classification.

The final segmented RGB image is shown in

Figure 2.

5 EXPERIMENTAL RESULTS

In this section we present some results obtained by

applying our segmentation scheme on microscopic

medical test images. Here we present the process of

the iterative RAG processing on a cytological image

that decreases the number of regions by 80%

without introducing clustering errors. Segmentation

results are presented in Figure 3 by showing the

SEGMENTATION OF MULTISPECTRAL IMAGES USING MATHEMATICAL MORPHOLOGY AND AUTOMATIC

CLASSIFICATION - Application to Microscopic Medical Images

239

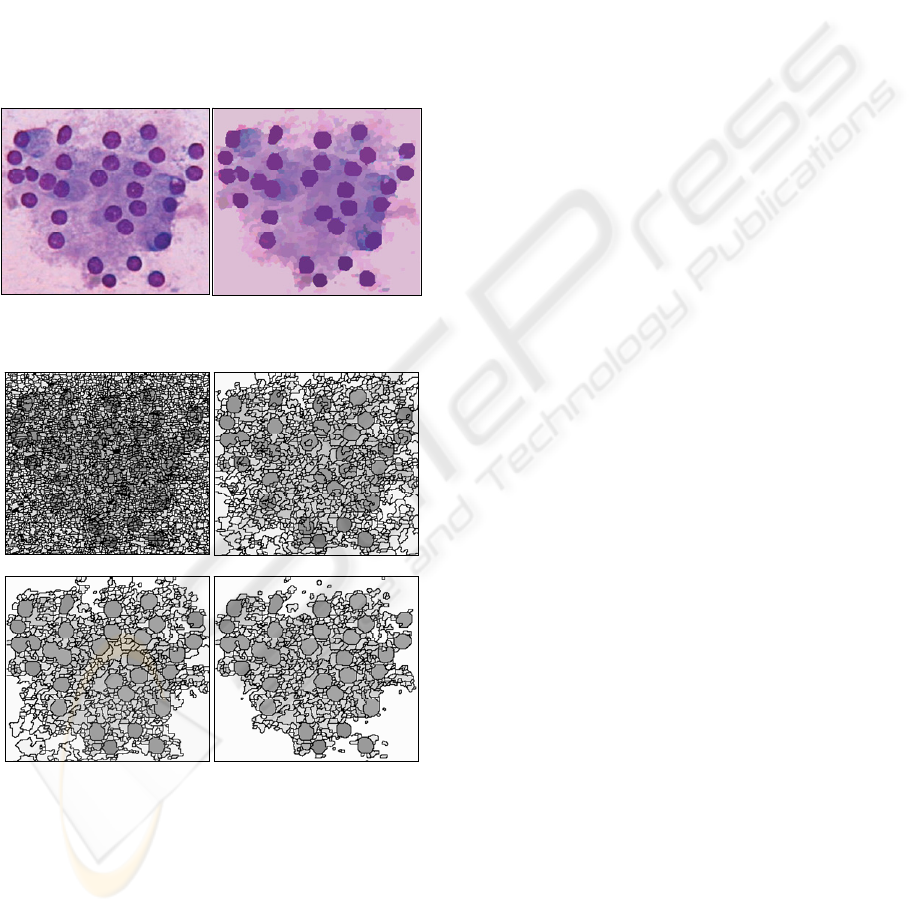
region borders showing the ability of the proposed

segmentation scheme to simplify the original image.

The use of morphological process as opening and

closing operations applied on the RAG yields an

interesting feature extraction as the photometric

value, the area, the perimeter, the compactness

factor, the number of neighbors of a region and their

relationship for each region. This description

represents the simplified information and contains

potentially an elaborate knowledge. After the

interpretation of the image, a list of retained objects

and their associated features are stored in an XML

(eXtensible Markup Langage) file and ready to be

integrated into a medical information system.

Figure 2: The original RGB image and its corresponding

segmented image.

(a)

(b)

(d)

(c)

Figure 3: Hierarchical RAG levels shown the step of

region merging.

6 CONCLUSIONS

We have proposed a new method of microscopic

medical images segmentation using mathematical

morphology applied on RAG and an automatic

clustering method followed by a regularization step

using an automatic hypercube classification. Due to

the unsupervised nature of the procedure especially

the use of automatic thresholds detection, it can be

reliable to the huge variability of intensities and

shapes of the image regions and will be tested as a

part of future work in other color space without

introducing

a priori knowledge and pre-processing

stages.

Results show the effectiveness of our method for

medical image applications as cytology images and

the impact that it introduces on the semantic high

level search for any disease or abnormal cells.

In this paper, the morphological operations

consider only the extrema of region neighborhood.

For future works, we will pursue the aggregation

operations beyond the limits presented by the

morphological processing avoiding the refinement

segmentation step that uses the hypercube

classification.

REFERENCES

Lucchese, L., Mitra, S.K., 2001. Color image

segmentation: A state-of-the art survey. In Image

Process. Vis. Pattern Recog. Proc. Indian Nat. Sci.

Acad. (INSA-A). Vol67 i2.pp. 207-221.

Lezoray, O., Lecluse, M., November 2007. Automatic

segmentation and classification of cells from broncho

alveolar lavage. In Image Analysis and Stereology,

Vol.26, pp. 111-119.

Lezoray, O., Juin 2003. Supervised automatic histogram

clustering and watershed segmentation. Application to

microscopic medical images. In Image Analysis and

Stereology, Vol. 22, Numéro 2, pp.113-120.

El-Khoury, E., Senac, C., André-Obrecht, R., 2007.

Speaker Diarization: Towards a more Robust and

Portable System. Int. Conf. On Acoustics, Speech, and

Signal Processing (ICASSP’2007), Honolulu, Hawaii,

USA.

Hirata Jr., R., César Flores, F., Barrera, J., Lotufo, R.,

Meyer, F., 2000. Color Image Gradients for

Morphological Segmentation. In XIII Brizilian

Symposium on Computer Graphics and Image

Processing (SIBGRAPI'00), pp.316-326.

Beucher, S., Lantuéjoul, C., Sept. 1979. Use of watersheds

in contour detection. In Int.workshop on image

processing, real-time edge and motion detection.

Mestar, A., Vannoorenberghe, P., Flouzat, G., April 2007.

Mathematical Morphology applied to Very High

Resolution Spatial images interpretation. In Urban

Remote Sensing Joint Event, pp. 1-7.

Pesaresi, M., Benediktsson, J.A., Feb. 2001. A new

approach for the morphological segmentation of high-

resolution satellite imagery. In Geoscience and

Remote Sensing,IEEE Transactions, Vol 39, Issue 2.

VISAPP 2009 - International Conference on Computer Vision Theory and Applications

240