ESTIMATION OF INERTIAL SENSOR TO CAMERA ROTATION

FROM SINGLE AXIS MOTION

Lorenzo Sorgi

Virtual Reality Laboratory, CIRA the Italian Aerospace Research Centre, Via Maiorise, Capua, Italy

Keywords:

Camera Calibration, Inertial Sensors, Camera Pose.

Abstract:

The aim of the present work is to deﬁne a calibration framework to estimate the relative orientation between a

camera and an inertial orientation sensor AHRS (Attitude Heading Reference System). Many applications in

computer vision and in mixed reality frequently work in cooperation with such class of inertial sensors, inorder

to increase the accuracy and the reliability of their results. In this context the heterogeneous measurements

must be represented in a unique common reference frame (rf.) in order to carry out a joint processing. The

basic framework is given by the estimation of the vertical direction, deﬁned by a 3D vector expressed in the

camera rf. as well as in the AHRS rf. In this paper a new approach has been adopted to retrieve such direction

by using different geometrical entities which may be inferred from the analysis of single axis motion projective

geometry. Their performances have been evaluated on simulated data as well as on real data.

1 INTRODUCTION

Vision based applications are becoming a standard in

many industrial ﬁelds due to the large availability of

low cost hardware and the rapidly increasing compu-

tational power of computer processors. Cameras are

often used in cooperation with other sensors in order

improve the detection capabilities and the reliability

of information extracted from images. One class of

devices frequently integrated within vision systems, is

given by the position and orientation sensors. As mat-

ter of fact the group INS/GPS/Vision has become a

standard in vision assisted navigation systems for land

and aerial vehicles (Templeton et al., 2007; Jang and

Liccardo, 2007; Kim and Sukkarieh, 2004; Merino

and al, 2006). In order to integrate inertial sensors

and cameras within a unique system, engineers usu-

ally count on the accuracy of the manual alignment

between sensors. Therefore the geometrical informa-

tion extracted from camera are assumed to be valid

also in the AHRS rf. and vice versa. This means that

the transformation between mapping 3D vectors from

the AHRS rf. onto the camera rf. is assumed equal to

the identity matrix. However in some cases this ap-

proach can be very limiting: in mixed reality applica-

tion for example the overlay of graphics layers on the

actual video, requires high accuray. In literature there

are very few works addressing such calibration prob-

lem. In (Catala et al., 2006) the alignment between

vehicle and an onboard camera has been tackled in

an uncalibrated framework using reference lines de-

tected from the road infrastructure. In (Lobo and

Dias, 2003; Lobo and Dias, 2004), which are speciﬁc

works on this topics, the authors use vertical direc-

tions measured from differently located camera to es-

timate the relative orientation between the AHRS and

the camera. This approach requires the localization of

the vanishing points corresponding to vertical lines in

3D space, which turned out to be a numerically unsta-

ble task. In this paper we propose a similar approach

where the vertical direction is inferred from different

geometrical entities: the planar homography induced

by a calibration object and the ellipses projected from

horizontal circles drawn in space by rotating objects.

Within this framework we have designed two tech-

niques which make use of an a-priori known object

and unknown object respectively, undergoing single

axis rotation motion under the action of gravity.

2 CALIBRATION SYSTEM

OUTLINE

Let us denote with v

a 3D vector in rf. A and with

A→B

the 3D rotation transforming any 3D vector

from rf. A to rf. B, i.e. v

= R

A→B

. We will

also assume to operate in calibrated cameras condi-

Sorgi L. (2009).

ESTIMATION OF INERTIAL SENSOR TO CAMERA ROTATION FROM SINGLE AXIS MOTION.

In Proceedings of the Fourth International Conference on Computer Vision Theory and Applications, pages 13-19

DOI: 10.5220/0001754500130019

 SciTePress

tion, which means that the internal camera parame-

ters are assumed known. Therefore in the sequel, any

vector in the camera rf. will be identiﬁed by its nor-

malized metric coordinates.

The set of sensors within the AHRS provides the

parameters of the 3D rotation representing its orien-

tation with respect to the local East-North-Up (ENU)

rf. In aeronautical notation 3D rotations are usually

parameterized using the YXZ Euler-angles represen-

tation, which factorizes the attitude rotation as a se-

quence of three rotations about the coordinate axis:

ENU→AHRS

(α, β, γ) = R

(α)R

(β)R

(γ) , where

(γ, β, α) are denoted as Heading, Pitch and Roll re-

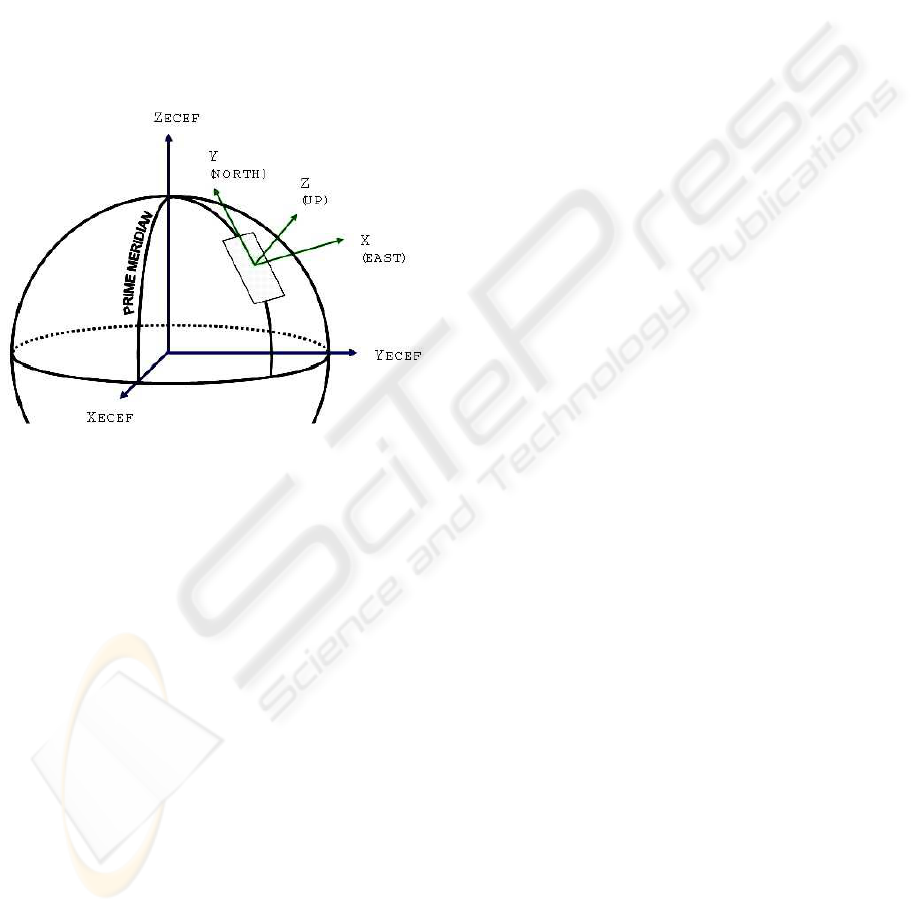
spectively (Fig.1).

Figure 1: A plane tangent to the hypothetical spheroid sur-

face contains the local East North directions, which set

those axis for the East-North-Up reference frame.

Let us assume we are given a camera rigidly attached

to an AHRS, so that we can express the camera atti-

tude as a composition of a two rotations:

ENU→Cam

= R

AHRS→Cam

ENU→AHRS

. (1)

Our objective is to estimate R

AHRS→Cam

, which rep-

resents the unknown in the previous relation. Such a

rotation could be easily estimated from a set of N pairs

of corresponding vectors V = {v

AHRS

, v

Cam

}

i=1..N

where any pair represents the same direction in 3D

space, expressed as vector in the AHRS and in the

camera rf. respectively. Once the set V is known, the

rotation R

AHRS→Cam

is simply given by the solution

to the minimization problem:

AHRS→Cam

= min

R ∈SO(3)

∑



Cam

− R v

AHRS



. (2)

This is a classical problem of rotation ﬁtting, widely

studied in literature, which can be solved using sev-

eral different methods. In this work we used the

approach based on the Singular Value Decomposi-

tion (SVD), described in (Kanatani, 1994). What is

needed is a procedure to build the set V, identifying

those 3D directions which may be estimated in a reli-

able way both in the camera and the AHRS rf. The so-

lution proposed in (Lobo and Dias, 2003; Alves et al.,

2003; Lobo and Dias, 2007) and revisited in this pa-

per, involves the exploitation of the vertical direction,

denoted for clarity by the vector UP

ENU

= [0, 0, 1]

In the original paper the authors used the projection

of scene vertical lines, retrieved from a calibration

checkerboardplaced vertically. We notice that this ap-

proach may result in a poor estimation due to the nu-

merical instability of vanishing points measurement

and to the difﬁculty to reach a high accuracy in the

positioning of the calibration object. Instead, we ob-

serve that the vertical direction can be represented by

any object hanging by a thread, only undergoing ac-

tion of gravity. Therefore, as an alternative solution

we propose to use different geometrical entities in-

ferred from the projectivegeometry of single axis mo-

tions, which can be robustly estimated from the tracks

left on the image plane during the object revolution

motion.

The full procedure is performed into two main

steps. In the ﬁrst one we build the set V by iterat-

ing a basic processing unit which is performed with

ﬁxed acquisition system and rotating calibration ob-

ject. Any iteration is performed with different orien-

tation of the acquisition system and provides a pair

of corresponding vectors (UP

Cam

, UP

AHRS

). The vec-

tor UP

Cam

is computed from the different geometri-

cal entities inferred by the assumption of single axis

motion (two different technique will be presented),

while UP

AHRS

is trivially given by the third column

of the AHRS orientation matrix R

ENU→AHRS

, directly

computed from the attitude angles Heading, Pitch and

Roll. The second step is the SVD-based estimation

of the rotation best describing the transformation be-

tween the vectors sets.

It is worth to underlinethat the pose of the camera-

AHRS system is not changed during one iteration of

the calibration procedure, then the orientation mea-

surement provided by the AHRS is constant up to

an additive noise, assumed approximately white zero

mean Gaussian. Under this assumption the Maximum

Likelihood estimation of R

ENU→AHRS

is simply ob-

tained by averaging the set of the collected orienta-

tion matrices. The averaging operation over the group

SO(3) is perfomed by means of the QR decomposi-

tion, as described in (Moakher, 2002).

VISAPP 2009 - International Conference on Computer Vision Theory and Applications

−0.5

0.5

−0.5

0.5

−0.8

−0.6

−0.4

−0.2

0.2

0.4

0.6

0.8

Cam

Figure 2: The two frames on the left show the rotation of the calibration planar object about the vertical direction, used as

basic calibration step. The plot on the right shows an example of vertical direction estimation in camera reference frame,

using the horizontal plane spanned by the vector Z

Cam

, normal to the calibration object, during one single-axis motion. In

blue is drawn the vector UP

Cam

estimated by linear regression.

3 CALIBRATION FROM PLANAR

HOMOGRAPHY

The ﬁrst proposed technique uses as calibration tool a

planar checkerboard hung down a ﬁxed point through

a thread. The object undergoes a rotation around the

vertical axis by applying a small twisting to the thread

(Fig. 2).

It is well know that the perspective projection of a

3D plane Π onto an image, is described by a homog-

raphy. If we introduce a rf. Ob j, aligned to Π with the

Z-axis parallel to the plane normal, then the equation

of Π is given by Z = 0 and the homography from the

plane Π to the image plane factorizes as:

Obj→Cam

= [r

Cam

], (3)

where r

and r

are the ﬁrst two columns of the ma-

trix R

Obj→Cam

which describes the relative orienta-

tion between the camera and the rf. Obj, T

Cam

is the

translation vector expressed in the camera rf. (Zhang,

2000). Under the camera rigid motion, the Z-axis

(normal to Π) transforms as:

Cam

= R

Obj→Cam

[0, 0, 1]

= r

= [r

]

(4)

where [·]

is the skew symmetric matrix equivalent

to the cross product operation. Therefore from the

planar homography (3) one can easily determine the

vector Z

Cam

. Since the planar object undergoes ro-

tation motion around the vertical axis, we can gather

that during such a motion the vector Z

Cam

spans the

horizontal plane. Therefore the sequence of homo-

graphies {H

Obj→Cam

}

i=1...M

computed during the ob-

ject rotation, will provides by factorization the set of

vectors lying on the horizontal plane {Z

Cam

}

i=1...M

where M is the number of images collected during the

object revolution. Then the vertical direction UP

Cam

assumed ﬁxed during the object motion, is estimated

by linear ﬁtting as the solution to the minimization

problem (Fig. 2):

Cam

= min

v∈R

∑

j=1

Cam

. (5)

4 CALIBRATION FROM

CIRCULAR POINTS

In the previous section we proposed a technique to

estimate the vector UP

Cam

from a sequence of pla-

nar homographies, obtained during the rotation of a

known planar calibration object. We now present a

slightly more uncalibrated approach which does not

require any a-priori known planar object, but keeps

only the assumption of single axis motion around the

vertical axis.

Let’s deﬁne a virtual rf. Obj, aligned with the Z axis

parallel to the vertical direction and the X − Y axis

spanning the horizontal plane Π. On the projective

plane Π the line at inﬁnity l

Obj

∞

∼ [0, 0, 1]

is trans-

formed by the projectivity (3) in the corresponding

vanishing line l

Cam

∞

, in the image space :

Cam

∞

∼



Obj→Cam



−T

Obj

∞

. (6)

By substituting the structure of the planar homogra-

phy (3) in the relation



Obj→Cam





Obj→Cam



−T

= I

3×3

, one can de-

duce that then the third column of



Obj→Cam



−T

must be the orthogonal to both r

and r

. We can

then parameterize the line-projectivity as:



Obj→Cam



−T

∼ [a|b|r

]. (7)

ESTIMATION OF INERTIAL SENSOR TO CAMERA ROTATION FROM SINGLE AXIS MOTION

Figure 3: Simple 1D calibration tool. Notice that in principle any object with unknown geometry could be used, since the

technique relies only on feature tracks. On the right are shown the three ellipses ﬁtted from the tracked features.

for some a,b∈ R

which can be left undetermined for

our purposes. By substituting (7) in the equation (6)

we obtain:

Cam

∞

∼ r

= UP

Cam

. (8)

Notice that r

is the representation of the vertical di-

rection in the camera rf., therefore the identiﬁcation

in the image plane of the vanishing line l

Cam

∞

corre-

sponding to the 3D horizontal plane, directly gives the

metric measure of the vector UP

Cam

. We will estimate

the homogeneousvector representing the line l

Cam

∞

, by

searching the images of the Circular Points.

Let P ∈ R

be a 3D point undergoing circular

motion around the vertical axis: necessarily P will

describe a circular trajectory laying on a horizontal

plane. To this curve belong two complex points, de-

noted as Circular Points (CPs) due to the fact that they

also lie on any circle in the projective plane (Hart-

ley and Zisserman, 2004). The CPs are expressed in

2D homogeneouscoordinates by J

Obj

∼ [1, i, 0]

and

Obj

∼



Obj



∗

, where the notation (·)

∗

means com-

plex conjugate. By direct inspection of the circular

points coordinates, one can easily see that they also

belong to the line at inﬁnity identiﬁed by the inter-

section of Π with the plane at inﬁnity. In 3D pro-

jective space they actually represent the intersections

of any circle lying on any plane parallel to Π with

the plane at inﬁnity. This property holds under any

arbitrary projective transformation and therefore the

images of all the 3D circles lying in the 3D space in

some plane parallel to Π, will have a common pair of

complex points, given by the images of the circular

points, J

Cam

and J

Cam

. As in 3D space, they also be-

long to the vanishing line l

Cam

∞

(our objective), which

therefore can be estimated as:

Cam

∞

∼ [J

Cam

]

Cam

= [J

Cam

]



Cam



∗

. (9)

As we pointed out the circular points lie on all cir-

cles in the projective plane, therefore their images



Cam

, J

Cam



, can be estimated as the intersection of

the images of at least three horizontal circles. In our

calibration framework these curves are actually el-

lipses, since we assumed that the 3D circles virtually

drawn in the space by the rotating object, are fully

contained in the camera semi space z > 0, i.e. they are

not (even partially) behind the camera. As stated by

the Bezout Theorem any two ellipses in the 2D pro-

jective space have four intersection points. Given that

the two ellipses are the projection of concentric cir-

cles lying on parallel planes in 3D, we can infer that at

least two of them are complexconjugate and represent

the images of the circular points. An indeterminacy

raise when two ellipses do not intersect on real points

but on two pairs of complex conjugate points. In this

case it not possible to discriminate between the two

pairs in order to choose the points



Cam

, J

Cam



. Such

an indeterminacy can be removed simply searching

for the common points among three (instead of just

two) ellipses in the image plane. This is the reason

why we claimed that the images of three parallel cir-

cles are actually needed.

A simple tool like the one shown in Fig. 3 is an

example of an object which can be used in the calibra-

tion procedure to draw horizontal circles in 3D space,

in substitution of the planar checkerboard used in the

previous section. Notice this is just a possible solu-

tion, appealing because the white dots on the rod can

be easily tracked in the video sequence, but in princi-

ple any unknown object could be used, since the tech-

nique is based on conic ﬁtting from any feature track.

Once the three conics are estimated the intersection

points are pair-wise computed. We expect that a pair

of complex conjugate points appear in both the two

VISAPP 2009 - International Conference on Computer Vision Theory and Applications

0 0.5 1 1.5 2 2.5 3 3.5 4 4.5 5

0.2

0.4

0.6

0.8

1.2

1.4

1.6

1.8

[deg]

0 0.5 1 1.5 2 2.5 3 3.5 4 4.5 5

0.2

0.4

0.6

0.8

1.2

1.4

1.6

1.8

[deg]

0 0.5 1 1.5 2 2.5 3 3.5 4 4.5 5

0.2

0.4

0.6

0.8

1.2

1.4

1.6

1.8

[deg]

0 0.5 1 1.5 2 2.5 3 3.5 4 4.5 5

0.2

0.4

0.6

0.8

1.2

1.4

1.6

1.8

[deg]

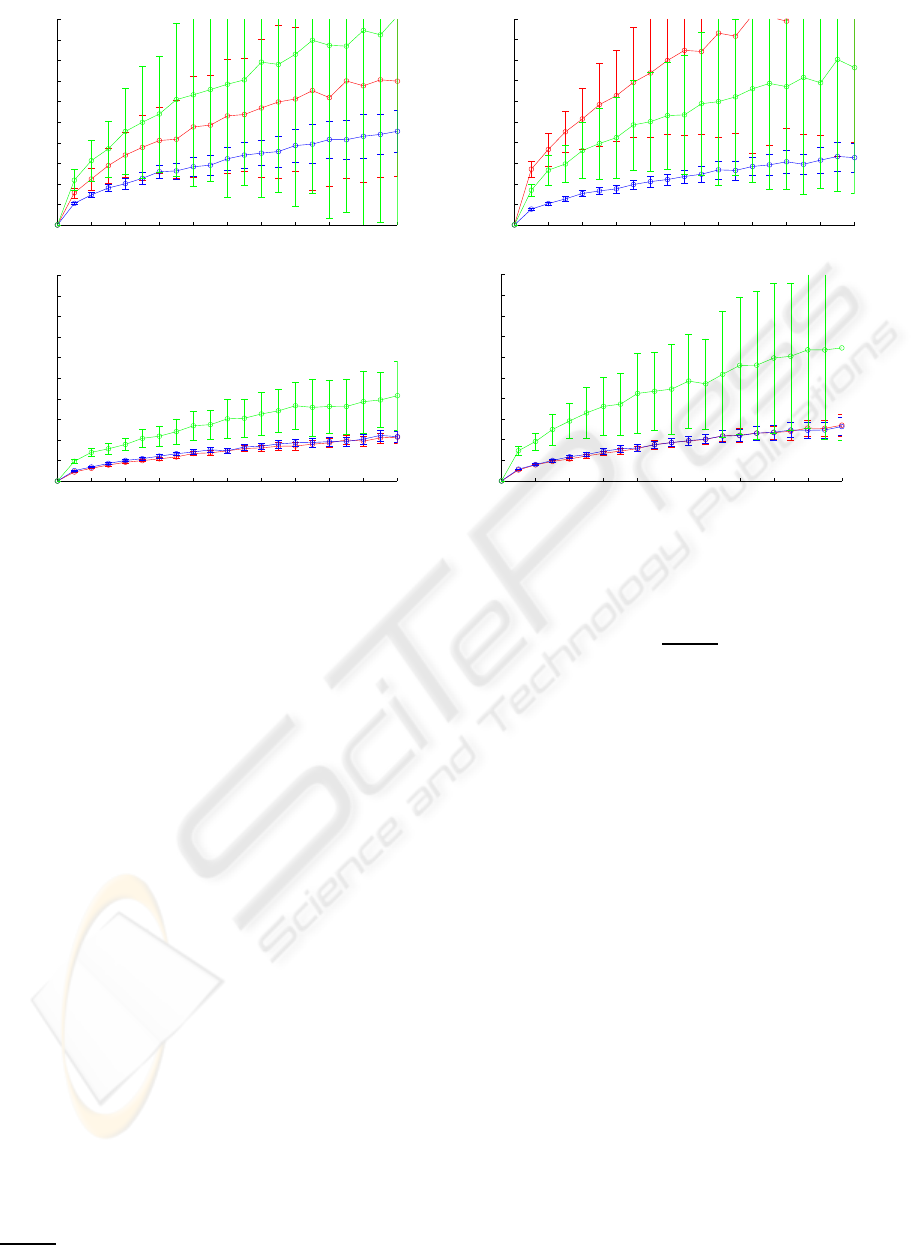
Figure 4: Result obtained on simulated data. The plots show the mean value and variance of the estimation error (10) for

increasing value of the additive Gaussian noise corrupting the image point coordinates. The line colors are used to discriminate

among the three evaluated techniques: the blu line for planar homography, the red line for the conic ﬁtting and the green line

for the vanishing points respectively.

sets of intersections, then we choose the point closest

to the two set as the image J

Cam

of one circular point.

Finally from (9) we can estimate the rotation axis, i.e.

the vertical direction UP

Cam

5 RESULTS

A wide series of tests has been carried out on sim-

ulated data in order to evaluate the performance of

the algorithms described in section 3 and 4, compared

with the technique based on vanishing points (Alves

et al., 2003). In each test the synthetic camera ori-

entation is slightly modiﬁed by an additional rotation

randomly selected in the neighbourhood of the iden-

tity matrix and the image points are corrupted by ad-

ditive Gaussian noise: the basic block of tests collects

ﬁve hundreds of these trials. Twenty test-blocks have

been carried out with increasing variance of the ad-

ditive Gaussian noise. This complete sequence has

been repeated for four different camera locations, in

order to evaluate the capability of algorithms to cope

with viewing slant with respect to the calibration ob-

ject. The estimation error has been deﬁned in terms of

angular distance between the real vertical direction,

Cam

and the estimated one, UP

Cam

= cos

−1



Cam



. (10)

The results from the three evaluated techniques are

presented in Fig.4.

In order to provide a fair comparison the three

techniques have been tested in their linear form. The

ﬁnal calibration module implements the technique

presenting the best performance as initialization for

a non linear reﬁnement step, based on the Levenberg-

Marquardt iterative algorithm to minimize the corre-

sponding geometric error.

It is evident that the approach based on planar ho-

mography guarantees the best performance and there-

fore has been selected for calibrating real sensors.

The employed system is composed by a low cost in-

ertial sensor rigidly attached to a (768 X 576) ana-

log camera (Fig.4.c). The quality of the estimated

relative orientation between the camera and inertial

sensors (Fig.5), is evaluated by computing the mean

value of the reprojection error between the two sets of

estimated vectors (0.6422

◦

) and its variance (0.2217).

6 CONCLUSIONS

A framework to estimate the relative orientation be-

tween an inertial sensor and a camera by using the

ESTIMATION OF INERTIAL SENSOR TO CAMERA ROTATION FROM SINGLE AXIS MOTION

(a)

−1

−0.5

0.5

−0.5

0.5

−0.8

−0.6

−0.4

−0.2

0.2

0.4

0.6

0.8

1.3694

0.35916

0.30095

0.31158

0.87006

(b)

Figure 5: Calibration results on real acquisition system. (a) On the left the system composed by the camera and the rigidly

attached AHRS. On the right (b) the calibration directions obtained from ﬁve different sequences, presented as a set of vectors

pairs V = {UP

AHRS

, UP

am}

i=1..5

. The red and blue lines are the vectors expressed in the AHRS r.f. and in the camera

r.f. respectively. In green are drawn the rotated vectors R

AHRS→Cam

AHRS

, obtained by using the estimated rotation, with

the indication of the angular error expressed in degrees. The last two rows present an application of the technique for video

stabilization: the ﬁrst three images are raw frames selected from a video sequence, the last row presents the same frames

stabilized in Pitch and Roll.

projective geometry of revolution motions about the

vertical axis, has been presented. The main contri-

bution of this work is provided by the exploitation of

conics and planar homographies for the estimation of

the vertical direction in the camera rf., which playes

a central role for the camera attitude estimation. The

choice of these geometrical entities is supported by

the stability of the numerical ﬁtting algorithms, which

can cope with severeslant between the camera and the

calibration structure. In the paper we have been pre-

sented results on simulated as well as real data, which

showed that among the three compared approaches,

the planar homography is the geometrical entity best

ﬁtting this sort of problems.

REFERENCES

Alves, J., Lobo, J., and Dias, J. (2003). Camera-inertial

sensor modelling and alignment for visual navigation.

VISAPP 2009 - International Conference on Computer Vision Theory and Applications

In 11th Int. Conference on Advenced Robotics, pages

1693–1698.

Catala, P. A., Rataj, J., and Reulke, R. (2006). Self-

calibration system forthe orientation of a vehicle cam-

era. International Archives of Photogrammetry and

Remote Sensing, XXXVI(5):68 – 73.

Hartley, R. and Zisserman, A. (2004). Multiple View Geom-

etry in Computer Vision. Cambridge University Press,

ISBN: 0521540518, second edition.

Jang, J. S. and Liccardo, D. (2007). Small uav automation

using mems. IEEE Aerospace and Electronic Systems

Magazine, 22(5):30–34.

Kanatani, K. (1994). Analysis of 3-d rotation ﬁtting. IEEE

Trans. Pattern Anal. Mach. Intell., 16(5):543–549.

Kim, J. and Sukkarieh, S. (2004). Autonomous air-

borne navigation in unknown terrain environments.

Aerospace and Electronic Systems, IEEE Transac-

tions on, 40(3):1031–1045.

Lobo, J. and Dias, J. (2003). Vision and inertial sensor co-

operation using gravity as a vertical reference. IEEE

Trans. Pattern Anal. Mach. Intell., 25(12):1597–1608.

Lobo, J. and Dias, J. (2004). Inertial sensed ego-motion for

3d vision. J. Robot. Syst., 21(1):3–12.

Lobo, J. and Dias, J. (2007). Relative pose calibration be-

tween visual and inertial sensors. Int. J. Rob. Res.,

26(6):561–575.

Merino, L. and al (2006). Vision-based multi-uav posi-

tion estimation. Robotics and Automation Magazine,

IEEE, 13(3):53–62.

Moakher, M. (2002). Means and averaging in the group

of rotations. SIAM Journal on Matrix Analysis and

Applications, 24(1):1–16.

Templeton, T., Shim, D. H., Geyer, C., and Sastry, S.

(2007). Autonomous vision-based landing and ter-

rain mapping using an mpc-controlled unmanned ro-

torcraft. In Robotics and Automation, 2007 IEEE In-

ternational Conference on, pages 1349–1356.

Zhang, Z. (2000). A ﬂexible new technique for camera

calibration. IEEE Trans. Pattern Anal. Mach. Intell.,

22(11):1330–1334.

ESTIMATION OF INERTIAL SENSOR TO CAMERA ROTATION FROM SINGLE AXIS MOTION