GPU-BASED REAL-TIME DISCRETE EUCLIDEAN DISTANCE
TRANSFORMS WITH PRECISE ERROR BOUNDS
Jens Schneider, Martin Kraus and R¨udiger Westermann
Computer Graphics & Visualization Group, Technische Universit¨at M¨unchen
Boltzmannstraße 3, 85748 Garching b. M
¨
unchen, Germany
Keywords:
Discrete euclidean distance transform, Graphics processing unit, SIMD-parallelism.
Abstract:
We present a discrete distance transform in style of the vector propagation algorithm by Danielsson. Like other
vector propagation algorithms, the proposed method is close to exact, i.e., the error can be strictly bounded
from above and is significantly smaller than one pixel. Our contribution is that the algorithm runs entirely
on consumer class graphics hardware, thereby achieving a throughput of up to 96 Mpixels/s. This allows the
proposed method to be used in a wide range of applications that rely both on high speed and high quality.
1 INTRODUCTION
Algorithms that depend on distance transforms
(Rosenfeld and Pfalz, 1966) or Voronoi diagrams
(Voronoi, 1908) seem to be ubiquitous. For instance,
the automatic analysis of real-time video images at
ever increasing resolutions, medical data processing,
and artistic applications are just a few examples of
a widely established technique. In nearly all cases
that require distance transforms, algorithms capable
of achieving throughputs of several million pixels per
second are highly advantageous. Especially if the re-
sults are to be visualized immediately, it is a natu-
ral choice to perform data processing and filtering di-
rectly on the same commodity class graphics hard-
ware used for visualization. To tap the graphic pro-
cessing unit’s (GPU) superior memory bandwidth and
computing power, however, special SIMD-like pro-
gramming paradigms have to be employed and com-
munication with the host CPU must be minimized.
Especially the latter has led to a rich catalogue of
GPU-based modules for various tasks. Unfortunately,
distance transforms and Voronoi diagrams running di-
rectly on the GPU are currently either fast or precise.
To address this disparity, we present a novel algo-
rithm based on the vector propagation paradigm pro-
posed in (Danielsson, 1980). Our algorithm is able to
approximate discrete Euclidean distance transforms,
Voronoi diagrams, and generalized Voronoi diagrams
entirely on a GPU, thus achieving up to 96 Mpixels
per second. Like other vector propagation methods it
is close to exact, i.e., errors are very unlikely to occur,
and each error can be bounded from above. While
the original paper provides a bound of less than 0.09
pixels, we provide a strict bound of
√
485−
√
481 <
0.091034 pixels for our method. Since the average er-
ror is generally negligible, our method can be used for
any practical purpose. Some results of the algorithm
are shown in Figure 1.
The rest of the paper is organized as follows. In
the next section, we review related work. After that
we briefly state the problem to be solved by our
approach. In Section 4 we then present our algo-
rithm and we describe the actual implementation us-
ing the DirectX API. Our results are presented in Sec-
tion 5, followed by conclusions and directions for fu-
ture work.
2 RELATED WORK
In this section we give a short overview over related
work. For an exhaustive review of prior art we would
like to refer the reader to (Jones et al., 2006; Cuise-
naire, 1999). Furthermore, a broad overvier of the
construction and applications of Voronoi diagrams
is provided in (Aurenhammer, 1991; Okabe et al.,
1999).
Considerable effort has been spent in order to ac-
celerate the computation of distance transforms as
much as possible. The most promising algorithms ap-
proximate or solve the aforementioned problems by
using a sweeping strategy in O (N) (Danielsson, 1980;
435
Schneider J., Kraus M. and Westermann R. (2009).
GPU-BASED REAL-TIME DISCRETE EUCLIDEAN DISTANCE TRANSFORMS WITH PRECISE ERROR BOUNDS.
In Proceedings of the Fourth International Conference on Computer Vision Theory and Applications, pages 435-442
DOI: 10.5220/0001754604350442
Copyright
c
 SciTePress

Figure 1: From left to right: A generalized Voronoi diagram using points and curves as sites, an artistic Voronoi-based
mosaicking filter using Gaussian-distributed sites, and a Voronoi diagram consisting of first- (red lines) and second-order
(green lines) neighbor regions (please refer to the electronic version). Each image has a resolution of 1600 ×1200 and was
generated completely on a GPU. The two left images took less than 22 ms, the rightmost image took less than 31 ms.
Mullikin, 1992; Satherly and Jones, 2001), where N
is the amount of pixels in the image. In contrast, algo-
rithms following the wavefront propagation principle
such as the fast marching method (Tsitsiklis., 1995;
Sethian, 1996; Helmsen et al., 1996) typically result
in a complexity of O (max(N,k ·log
2
k)), where k is
the amount of features.
Among the first approaches to approximate the
distance transform were those that replace the Eu-
clidean distance metric by more tractable ones such as
the Manhattan distance (Telea and van Wijk., 2002),
chamfer metrics (Rosenfeld and Pfalz, 1966; Butt and
Maragos, 1998; Svensson and Borgefors, 2002), or
octagonal metrics (Kulpa and Kruse, 1979). Espe-
cially chamfer metrics allow for a trade-off between
performance and error, but the distance fields com-
puted with these metrics may not be acceptable in
some cases due to the inherent approximation errors.
Another class of methods tries to generate a dis-
tance transform that is accurate for virtually all pixels
with only spurious errors. The most prominent exam-
ple is called vector propagation (Danielsson, 1980).
Although being conceptionally simple, highly accu-
rate results can be achieved with good performance
(Jones et al., 2006). These methods store a vector-
valued pointer to a feature candidate for each pixel.
These pointers are then propagated using a structur-
ing element called vector template . Multiple such
templates are sweeped in a simple fashion across the
image. Danielsson describes two methods, 4SED
and 8SED (SED being an acronym for sequential Eu-
clidean distance
), that effectively operate on a von
Neumann- and a Moore-neighborhood. 4SED is obvi-
ously faster and results in larger approximationerrors.
Recently a practical algorithm to compute a pre-
cise discrete distance transform in O (N) was pro-
posed (Maurer et al., 2003). However, this algorithm
relies on frequent concurrent read/write accesses—a
very limited feature on GPUs that is not yet exposed
in standard graphics APIs.
On a different avenue the use of GPUs has been
mandated by several authors. The potential of GPUs
for various computational geometry tasks is discussed
in (Denny, 2003). Closely in style to the continuous
sweepline algorithm (Fortune, 1986), the use of tri-
angle meshes to model a local distance field around
each feature is proposed in (Hoff et al., 1999). Hard-
ware depth-testing is exploited during rendering these
meshes to generate a generalized Voronoi diagram.
The distance transform can then be obtained from the
depth buffer. For applications that only need a dis-
tance transform in a shell around features, variations
of wavefront propagation methods have been shown
to be highly efficient. Using graphics hardware, such
methods extrude features to prisms and wedges which
can be scan-converted efficiently (Mauch, 2003; Sigg
et al., 2003). Although these approachesgenerate pre-
cise results, they rely on generating triangle meshes
and/or volumetric primitives, and their complexity
is not independent of the number of features. To
avoid excessive rasterization of distance meshes, a
GPU-based framework to compute 3D distance trans-
forms using slice-based culling and clamping was
proposed in (Sud et al., 2004). Splatting the distance
functions for each feature point (Strzodka and Telea,
2004) avoids the generation of meshes, but although
even skeletons can be constructed this way, these ap-
proaches tend to be severely fill-rate-bound due to
overdraws.
In (Rong and Tan, 2006) the jump flooding
paradigm was presented, a communication pattern
to quickly propagate information in highly SIMD-
parallel computing environments such as GPUs. This
method is among the most promising ways to com-
pute distance transforms and generalized Voronoi di-
agrams since it offers a flexible trade-off between pre-
cision and speed.
VISAPP 2009 - International Conference on Computer Vision Theory and Applications
436

3 PROBLEM DESCRIPTION
Throughout the description the notion of a feature
will be used to describe the geometric entities that will
eventually become Voronoi sites. Features are distin-
guished by pairwise different IDs. In case of the clas-
sical Voronoi diagram, features are points. Among the
generalizations commonly made, one allows lines and
curve-segments as features. To be able to construct
such generalized Voronoi diagrams (see Figure 1, left-
most image), we extend the notion of a feature to re-
fer to any non-empty set of (potentially disconnected)
points that share an ID.
Given a set of points P := {p
i
}
N
i=1
⊂ R
n
and
a set of features S :=

F
j

k
j=1
, F
j
⊆ P, an al-
gorithm that computes a scalar field Φ(p
i
) :=
min
j∈{1,...,k}
min
f∈F
j
kp
i
− fk
2
is said to compute
a discrete Euclidean distance transform of (P,S).
Note that according to the definition of S, all
points used as a feature are contained in P, which
is a convention that does not affect generality.
An algorithm that computes a labeling L(p
i
) :=
argmin
j∈{1,...,k}
min
f∈F
j
kp
i
− fk
2
is said to compute
a (generalized) discrete Voronoi diagram of (P, S).
These two problems are closely related; in fact the
above definitions can be turned directly into a na¨ıve
algorithm with complexity O

N ·|∪
j∈{1,...,k}
F
j
|

to
compute both. Note that in the continuous case a
practical algorithm of complexity O (k ·log
2
k) is only
known for the classical Voronoi diagram. Since the
bounding curves and surfaces of the regions of contin-
uous generalized Voronoi diagrams can be algebraic
surfaces of arbitrary degree, a practical algorithm is
not known.
4 ALGORITHM
We will first review the original vector propagation
algorithm before adressing the changes necessary in
order to execute the algorithm on the GPU efficiently.
For simplicity’s sake, we will first assume all features
to be single points and extend this restriction later to
the generalized case.
4.1 Vector Propagation
Given an N × M image of quadratic pixels P :=
{(i, j)} ≡ {1,... ,N}× {1,.. . ,M}, a set of features
S ⊆ P, and a set of vector templates T := {{(k,l)} ⊂
Z
2
}, where {(k,l)} specifies pixel offsets belonging
to one template, vector propagation works as follows.
Initialization
(0) for each (i, j) ∈P
(1) if (i, j) ∈ S then v(i, j) ← (i, j)
(2) else v(i, j) ←(∞,∞)
(3) end
Propagation
(4) for each t ∈ T
(5) sweep each (i, j) ∈ P
(6) v(i, j) ← v

argmin
(l,m)∈t
d
l,m
+ (i, j)

,
(7) where d
l,m
:= kv(i+ l, j + m) −(i, j)k
2
(8) end
(9) end
Note that the sweeping steps (5) depend on the current
template’s shape. Each of the propagation updates
(steps 6 and 7) computes a new best candidate for the
feature closest to (i, j) by scanning the neighborhood
defined by the template t around (i, j) for possible
candidates. The templates originally used for 8SED
are depicted in Figure 2. The vectors in each cell de-
note the offset to the current pixel (i, j), since this is
the distance that has to be added to the current can-
didate of the respective cell to compute its distance to
(i, j) (hence (i, j) corresponds to the cell marked 0,0).
The arrows on the templates indicate the sweep direc-
tion, i.e., the leftmost template can be advanced from
left to right and top to bottom in either a row-major or
column-major sweep.
0,0−1,0 0,0
0,−1−1,−1 1,−1
0,0 1,0 −1,0 0,0
1,10,1−1,1
1,0
Figure 2: The 8SED vector templates proposed in (Daniels-
son, 1980).
4.2 GPU-based Implementation
The problem with the original vector templates is that
two row-major or column-major sweeps are required.
Such sweeps cannot be parallelized efficiently. A sim-
ple modification however will result in a sweepline
algorithm that can be efficiently implemented on a
SIMD-parallel GPU, albeit at the cost of a slightly
higher (by about 11%) memory bandwidth usage.
This modification is shown in Figure 3. We begin
1,1
−1,−1
−1,0
−1,1
0,0 0,0 1,0
1,−1
1,1
−1,−1 0,−1 1,−1
0,0 0,0
−1,1 0,1
Figure 3: Modified vector templates that can be swept in
four simple line-sweeps.
GPU-BASED REAL-TIME DISCRETE EUCLIDEAN DISTANCE TRANSFORMS WITH PRECISE ERROR BOUNDS
437

by storing the original image in an ID-texture using a
32 bit integer per pixel. Each pixel stores an ID > 0 if
it is a feature and 0 otherwise. Furthermore, we need
two textures for the vector propagation—since using
standard graphics APIs read and write accesses are
mutually exclusive—to store a 2D vector. We chose a
format of 2 × 16 bit unsigned integers per pixel. Ini-
tialization proceeds as described by the pseudo-code
in Section 4.1. More precisely, we bind both textures
as render targets and render a quad covering all tex-
els. For each texel we then perform a texture lookup
into the ID-texture. If the ID for the respective pixel
is 0, we store (2
16
−1,2
16
−1), which is the largest
possible number in the chosen format. Otherwise, we
store the fragment’s 2D position in pixel coordinates
(i.e., in the range [0... N −1] ×[0... M−1]). Prior to
performing the actual vector propagation we gener-
ate all necessary sweeplines in a single vertex buffer.
This buffer can be recycled for all input images of the
same resolution. In this way, frequent costly alloca-
tion of vertex buffers is avoided.
opposite sweep (analogously)
line copy
RR
W
W
R R
R
W
sweep
Figure 4: Mutual read/write exclusion on GPUs leads to
the so-called ping-pong buffering. The first sweep reads
from two lines of a shader resource texture and writes to
a single line of a render target texture. Updated lines are
indicated by ticks. Before the opposite sweep commences,
a single line must be copied in order to ensure that updated
information is properly propagated.
We then start by binding one of the now-initialized
textures as a (read-only) shader resource , and the
other one as a (write-only) render target . A single
line is then rasterized to cover a single row (verti-
cal sweeps) or column (horizontal sweeps) of texels
of the render target, thereby allowing SIMD-parallel
processing. For each fragment generated in this way,
four texels corresponding to the current template are
fetched from the source texture in a pixel shader.
From these texels a new best candidate is computed
according to the propagation algorithm. The result is
written to the render target. After each line a ping-
pong swap
is performed to exchange shader resource
and render target. The sweepline is then advanced by
one texel, and the sweep proceeds until the end of the
texture is reached.
After each sweep one of the two textures will con-
tain all updated even lines while the other will con-
tain all odd updates (see Figure 4). Normally this
requires a merge operation prior to the next sweep.
However, by grouping sweeps with opposite direc-
tions into pairs the merge operation is reduced to a
single line copy.
In this way, textures have to be merged only after
each pair of sweeps by rendering a quad that covers
the entire destination texture. For each fragment thus
generated, a pixel shader discards every second frag-
ment in order not to overwrite the updated rows or
columns in the render target. All surviving fragments
just copy their value from the source texture. After
this merge operation is completed, it is repeated anal-
ogously to update the other texture.
Once the propagation is finished, each fragment’s
ID is obtained by a simple lookup into the ID-texture.
Boundaries of Voronoi regions fall between pixels
where IDs change. The distance transform is ob-
tained by re-computing the distance between the clos-
est feature and the fragment’s position for each frag-
ment. By assigning the same ID to multiple pixels in
the ID-texture, generalized Voronoi diagrams are ob-
tained. Furthemore, by propagating k best candidates
and sorting them in each propagation update, k−NN
Voronoi diagrams (Cuisenaire, 1999) can be gener-
ated that have been employed in procedural texturing
and modeling (Olsen, 2004). The rightmost image
in Figure 1 shows such a diagram for k = 2, where
brightness corresponds to the difference in distance
between the second nearest and the nearest feature.
As a result, the brightness is strictly positive every-
where except at first-order Voronoi boundaries where
it vanishes.
The result of a complete run of this algorithm is il-
lustrated in Figure 5. Each diagram shows the classi-
fication of pixels after each sweep, including immedi-
ate merging of the two partial ping-pong results. After
the first sweep features “fan out” at a 90
◦
angle to the
right. The sweep in the opposite direction is not able
to correctly classify the two green cells to the right,
since they do not have any candidates to choose from
except for themselves. Note that such cases will al-
ways be removed with the next sweep and that such
“islands” cannot occur at the line at which the last
sweep begins, since one of the three prior sweeps
would have removed them. In this example two pix-
els have the same distance to the blue and the green
features. Their final classification is dependent on the
sweep- and the computation-order.
4.3 Errors in 2D Vector Propagation
Errors in vector propagation only occur if a pixel can-
not be “reached” by its closest feature during prop-
VISAPP 2009 - International Conference on Computer Vision Theory and Applications
438

Figure 5: Example computation of a Voronoi diagram using the proposed algorithm. From left to right: Original image with
three features, results after sweep to the right and left, and results after sweep down and up. In the final image, a precise
continuous Voronoi diagram has been overlaid. Pixels that are colored using green/blue can be associated with green or blue,
since they have exactly the same distance to the respective features.
agation. This means there is a pixel whose entire
Moore-neighborhood points to other features. Such
a situation is depicted in the left part of Figure 6.
The gray pixel in the upper right is closest to the
green feature, but cannot be reached because all its
neighbors are closer to other features. In terms of
Voronoi regions (bold black lines in the figure) this
means the existence of a Voronoi region that con-
tains the center of a pixel but no center of any of
its neighbors. Consequently, circles around each of
the “obstructing” points through their associated fea-
ture must not contain the feature that would be cor-
rect for the mis-classified pixel. As a conclusion, the
closer the actual feature of the mis-classified pixel is
to these circles, the higher the worst-case relative er-
ror. The relative error can be shown to be less or
equal to

√
170−
√
169

/
√
169 < 0.3% (Cuisenaire,
1999). This case is depicted in the left half of Fig-
ure 6: the correct distance between the green feature
and the gray pixel would be
√
169, while it is falsely
asigned a value of
√
170. In (Danielsson, 1980) the
r
Figure 6: Worst-case error analysis for 2D vector propaga-
tion. In both images, the gray point should be associated
with the green feature. However the gray pixel’s sight to
the green feature is obstructed by direct neighbors that are
closer or equally close to other features.
maximum absolute error was computed as ε
max
(r) =
r + γ −
p
r
2
−γ, where γ ≈ 1 − cos 24.4698
◦
and r
is the distance between the correct feature of a mis-
classified pixel and an obstructing pixel, resulting in
lim
r→∞
ε
max
(r) = γ ≈ 0.08982 pixels. However, in
our tests we found a larger absolute error for our
method. Running an exhaustive search on all configu-
rations of three features on a 32×32 image, we found
the error to be bounded by ε
max
≤
√
485 −
√
481 ≈
0.091033 pixels. The corresponding case is shown in
the right half of Figure 6. It is a very pathological
case, though, since two of the obstructing pixels are
equally far from the green feature and either the blue
or the red one. Never the less, depending on the prop-
agation order this can lead to the observed error. Note
also that in this case Danielsson’s assumption that the
mis-classified pixel is assigned the value r + 1 is no
longer valid. Since the absolute error decreases with
increasing r, this case results in the largest maximum
error possible.
4.4 Generalization to 3D
The algorithm can be extended to 3D in an almost
straightforward manner by replacing sweep lines by
planes. However, current APIs can only render into
xy-aligned slices of volumetric textures. Conse-
quently, both sweeps in z-direction are straightfor-
ward. For the other directions the volume has to be
rotated to make the current sweep-direction z-aligned.
This is done after each sweep-pair during the merging
of partial results. First, one of the two 3D textures is
merged into the other. Then, rotation is performed by
rendering a quad per texture slice and fetching from
the resource texture using rotated coordinates. Be-
fore writing the read vector pointers have to be rotated
as well. Once a rotated texture has been obtained, it
is copied to the other one and sweeping is repeated.
Note that this method only works for volumes that
have the same amount of voxels along each dimen-
sion.
To reduce the memory requirements from 3 ×
16 bits per voxel and texture to 32 bits, vector pointers
can be packed. If the target GPU supports bit opera-
tions in the shader (as all DirectX 10 compliant GPUs
do), this comes at little if any additional cost.
GPU-BASED REAL-TIME DISCRETE EUCLIDEAN DISTANCE TRANSFORMS WITH PRECISE ERROR BOUNDS
439

5 RESULTS AND DISCUSSION
In this section we provide results and perform a
thorough comparison to the jump flooding algorithm
(JFA) (Rong and Tan, 2006). Although other GPU-
based methods have been proposed recently, e.g., the
fast hierarchical algorithm (FHA) (Cuntz and Kolb,
2007), in our opinion JFA offers the best trade-off be-
tween speed and approximation error among all pre-
vious approaches.
5.1 Bandwidth & Runtime Complexity
First we will compute the memory traffic caused by
our method for an image of resolution N
2
, since this
is a major limiting factor. It is assumed that all refer-
ences to features will be stored as 2 × 16 bit integer
values. Each read and write access will be counted
separately.
During line-sweeps, for each rasterized pixel four
vectors are read and one is written. There are (N −
1) ·N ≈ N
2
intermediate output pixels per sweep.
Furthermore, after each pair of sweeps, a merge-
operation is necessary. This operation reads a total
of N
2
/2 pixels from one texture and copies them to
another buffer. Since this has to be performed in both
directions, it results in a total of 2 ·N
2
accesses. For
two pairs of sweeps less than (2·2·5+ 2)N
2
= 22N
2
32 bit accesses are made, thus resulting in less than
88 bytes of memory traffic per pixel.
In comparison, JFA requires log
2
N passes, each
writing N
2
intermediate output pixels. Per pixel, a
total of 9 values (modulo boundary cases) is read.
Hence, JFA results in about log
2
N ·N
2
·(9+ 1) mem-
ory accesses, or less than 40 ·log
2
N bytes per pixel.
Consequently, our method is less likely to become
bandwidth-limited than JFA for large images, since
its traffic per pixel is independent of the image reso-
lution.
Our method compares four distances per interme-
diate output pixel multiplied by four sweeps, while
JFA requires nine comparisons per intermediate out-
put pixel. Thus, the theoretical complexity of our
method is O

16×N
2

and O

9×N
2
·log
2
N

for
JFA, where N
2
is the image resolution.
However, it should be noted that the 2D JFA can
achieve competitive results, since it generally exploits
GPU parallelism better than 2D vector propagation.
5.2 Empirical Validation
All tests were run on an Intel Core2Duo 6600 pro-
cessor clocked at 2.4 GHz running Windows Vista.
The machine was equipped with 2 GB DDR2 RAM
and an NVIDIA GeForce 8800GTX with 768 MB
of video RAM. The CPU version of our algorithm
is carefully hand-tuned and runs on a single core to
maximize caching benefits. We were able to run
the jump flooding algorithm (JFA) (Rong and Tan,
2006) on the very same machine achieving about
185 fps for a resolution of 512
2
. This corresponds to
roughly 46.25 Mpixels/sec. JFA is likely to perform
differently in other resolutions, but sadly the original
OpenGL-based application is locked at 512
2
pixels.
Since the timings for JFA are incomplete, they are
omitted from Table 1.
Most notable in the results displayed in Table 1
is the sudden decrease in CPU performance at res-
olutions of 2048
2
which is due to cache limitations.
Since we store images on the CPU in x-major or-
der, at a resolution of 2048
2
sweeps in the x-direction
are about five times as expensive as sweeps in the y-
direction. The reason is that sweeps in the y-direction
are perfectly cache-coherent since in this case x-rows
can be processed sequentially. Different storage lay-
outs (i.e., block-major or Z-order) could alleviate this
problem to a certain extent, but were not investigated.
The problem is naturally aggravated in higher dimen-
sions, which is clearly seen in the 3D part of the table.
Even for very small volumes, caching issues and the
sheer amount of memory traffic prohibit better perfor-
mance.
On the GPU, caching issues only occur at 4096
2
,
and they are by far less severe than on the CPU. On
the other hand, for small resolutions the GPU’s per-
formance is comparable to the CPU implementation
or even less. The reason is that in this case the GPU
suffers from draw-call overheads and the relatively
small amount of parallelism due to the short lines be-
ing rasterized. For applications that require lots of
small images of identical resolutions to be processed,
the GPU’s sweet spot around 2048
2
can still be har-
nessed by first blocking these images to a larger one.
The distance transform can then be computed in par-
allel for multiple smaller images. This only requires
to not render the first line of each new image block
during sweeps to avoid results from one block of im-
ages to leak into the next one. In theory even higher
pixel rates than those reported in the table can be
achieved in this way, although at the cost of a higher
per-image latency.
To validate the likelihood of errors to occur and
to measure the magnitude of errors, we reproduced
the experiment of (Rong and Tan, 2006). Our method
was run on images of a resolution of 512
2
that were
randomly filled with varying amounts of Laplacian-
distributed features. Over 10,000 runs were gener-
ated for amounts of features between 100 and 10,000.
VISAPP 2009 - International Conference on Computer Vision Theory and Applications
440

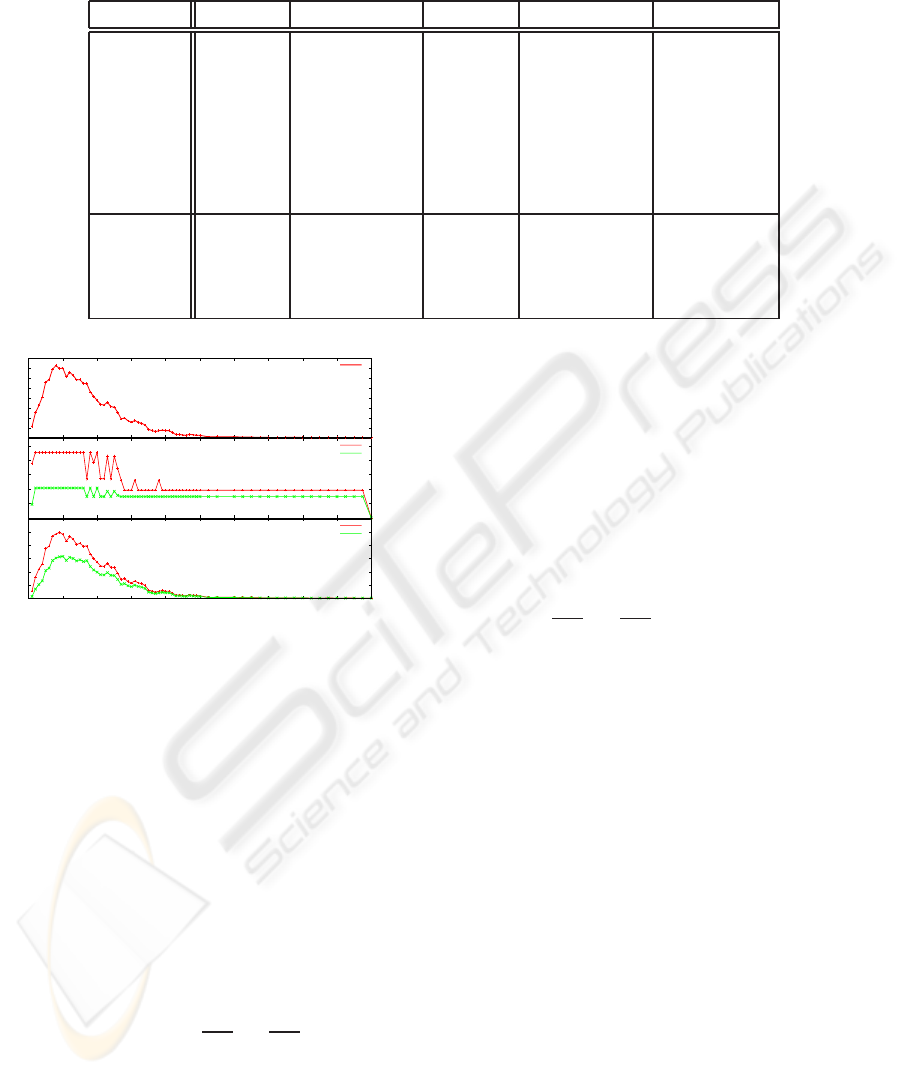
Table 1: Performance evaluation of our method. We specify both the time per frame in milliseconds and the achieved pixel
rate in pixels per second (1 Mpixel = 2
20
pixels, 1 Mvoxel = 2
20
voxels).
Resolution CPU time CPU pixel rate GPU time GPU pixel rate GPU Speedup
128
2
1.04 ms 14.96 Mpixel/s 2.50 ms 6.23 Mpixel/s 0.42×
256
2
4.60 ms 13.60 Mpixel/s 4.21 ms 14.84 Mpixel/s 1.09×
512
2
20.02 ms 12.49 Mpixel/s 7.42 ms 33.68 Mpixel/s 2.70×
1024
2
91.83 ms 10.89 Mpixel/s 15.14 ms 66.02 Mpixel/s 6.06×
2048
2
696.6 ms 5.74 Mpixel/s 41.68 ms 95.96 Mpixel/s 16.72×
4096
2
2751 ms 5.82 Mpixel/s 186.5 ms 85.79 Mpixel/s 14.74×
8192
2
11366 ms 5.63 Mpixel/s 1262 ms 50.70 Mpixel/s 9.00×
32
3
9.67 ms 3.23 Mvoxel/s 3.71 ms 8.42 Mvoxel/s 2.61×
64
3
84.18 ms 2.97 Mvoxel/s 8.21 ms 30.45Mvoxel/s 10.25×
128
3
1020 ms 1.96 Mvoxel/s 30.85 ms 64.83Mvoxel/s 33.08×
256
3
9195 ms 1.74 Mvoxel/s 213.0 ms 75.12Mvoxel/s 43.17×
0
0.001
0.002
0.003
0.004
0.005
0 1000 2000 3000 4000 5000 6000 7000 8000 9000 10000
0
0.01
0.02
0.03
0.04
0.05
avg. abs. error
avg. rel. error (%)
number of seeds
avg. abs. error/pixel
avg. rel. error/%
0
0.02
0.04
0.06
0.08
0.1
0
0.2
0.4
0.6
0.8
1
max. abs. error
max. rel. error (%)
max. abs. error/pixel
max. rel. error/%
0
0.02
0.04
0.06
0.08
0.1
0.12
0.14
0
0.08
0.16
0.24
0.32
0.4
0.48
0.56
errors per image
errors per Mpixel
avg. number of errors (512
2
images)
Figure 7: Top: Likelihood of an error to occur for different
amounts of features. Middle: Maximum absolute and rela-
tive errors. Bottom: Average absolute and relative errors.
From 100 to 5,000, the amount of features was var-
ied in steps by 100, and between 5,000 and 10,000 in
steps of 250. As can be seen in Figure 7, one of the
most interesting properties of this algorithm is that the
pathological cases leading to errors require a lot of
empty area and a very specific configuration of spuri-
ous features. Consequently, with increasing amounts
of features, the number of errors decreases. This is
especially useful for applications seeking to compute
distance transforms of contours, since errors are ex-
tremely unlikely to occur in this setting. For ran-
dom distributions of features the error rate was less
than 0.56 per Mpixel. The maximum absolute error
that occured was exactly
√
485−
√
481 pixels, as dis-
cussed in Section 4.3. The corresponding relative er-
ror is about 0.3%. Also, the average error that occured
was about one order of magnitude smaller, as can be
seen in the bottom diagram. This further indicates
that the maximum error is highly unlikely. Further-
more, the average error decreases with increasing dis-
tance, which is a feature specific to vector propagation
(Jones et al., 2006).
6 CONCLUSIONS
We have presented an algorithm to compute discrete
distance transforms, Voronoi diagrams, and gener-
alized Voronoi diagrams entirely on the GPU. This
method runs at high-speed and is precise in the sense
that the absolute error can be strictly bounded from
above by
√
485−
√
481 < 0.091034 pixels. Further-
more, errors are highly unlikely to occur.
The method will be especially benefitial to ap-
plications that already perform most of their work
on the GPU, but since practical bandwidths from
video- to host-memory are currently reaching about
2 GB/second, it could also be interesting for hybrid
CPU/GPU algorithms. Our approach can be easily
extended to 3D, and—although causing slightly more
memory traffic than other, purely tensor-product-
based approaches—the slow-down is less severe than
expected. This is mostly due to the fact that the raster-
ization of slices utilizes the GPU’s parallelism better
than the rasterization of lines.
In the future, we would like to investigate various
highly interesting avenues of research. Both skele-
tonization algorithms and signed distance transforms
are natural and very useful next steps. Also, the uses
of high-speed, high-quality discrete Voronoi diagrams
for artistic purposes are not yet fully explored. Many
commercially available painting tools already include
filters like mosaicking that are based on Voronoi dia-
grams. However, with the recent trend to ever higher
image resolutions (partly due to advances in CCD
technology), the time required to evaluate such fil-
GPU-BASED REAL-TIME DISCRETE EUCLIDEAN DISTANCE TRANSFORMS WITH PRECISE ERROR BOUNDS
441

ters is likely to become critical; and as a side-effect
rapid methods that allow for interactivity will offer
unprecedented benefits for artists in creating custom
filters.
REFERENCES
Aurenhammer, F. (1991). Voronoi diagrams–a fundamental
geometric data structure. ACM Computing Surveys,
23(3):345–405.
Butt, M. and Maragos, P. (1998). Optimum design of cham-
fer distance transforms. IEEE Trans. Image Process-
ing, 7(10):1477–1484.
Cuisenaire, O. (1999). Distance Transformation: Fast Al-
gorithms and Applications to Medical Image Process-
ing. Phd. thesis, Univ. Catholique de Louvain.
Cuntz, N. and Kolb, A. (2007). Fast hierarchical 3D dis-
tance transformations on the GPU. In Proceedings
Eurographics Short Papers, pages 93–96.
Danielsson, P. (1980). Euclidean distance mapping. Com-
puter Graphics and Image Processing, 14:227–248.
Denny, M. (2003). Algorithmic Geometry via Graphics
Hardware. Phd. thesis, Universit¨at des Saarlandes,
Saarbr¨ucken, Germany.
Fortune, S. (1986). A sweepline algorithm for Voronoi
diagrams. In ACM Symp. Computational Geometry,
pages 313–322.
Helmsen, J., Puckett, E., Colella, P., and Dorr, M. (1996).
Two new methods for simulating photolithography de-
velopment in 3D. In SPIE 2726, pages 253–261.
Hoff, K., T. Culver, J. K., Lin, M., and Manocha, D. (1999).
Fast computation of generalized Voronoi diagrams us-
ing graphics hardware. ACM Trans. on Graphics,
18(3):277–286.
Jones, M., Bærentzen, J., and Sramek, M. (2006). 3D dis-
tance fields: a survey of techniques and applications.
IEEE Trans. Visualization and Computer Graphics,
12(4):581–599.
Kulpa, Z. and Kruse, B. (1979). Methods of effective imple-
mentation of circular propagation in discrete images.
Internal Report LiTH-ISY-I-0274, Dept. of Electrical
Engineering, Link¨oping Univ., Sweden.
Mauch, S. (2003). Efficient algorithms for solving static
Hamilton-Jacobi equations. PhD thesis, California In-
stitute of Technology, Pasadena, CA.
Maurer, C., Qi, R., and Raghavan, V. (2003). A linear
time algorithm for computing exact euclidean distance
transforms of binary images in arbitrary dimensions.
IEEE Trans. Pattern Analysis and Machine Intelli-
gence, 25(2):265–270.
Mullikin, J. (1992). The vector distance transform in two
and three dimensions. CVGIP: Graphical Models and
Image Processing, 54(6):526–535.
Okabe, A., Boots, B., Sugihara, K., and Chiu, S. (1999).
Spatial Tesselations: Concepts and Applications of
Voronoi Diagrams. John Wiley & Sons Ltd.
Olsen, J. (2004). Realtime procedural terrain generation.
http://oddlabs.com/download/terrain generation.pdf.
Rong, G. and Tan, T.-S. (2006). Jump flooding in gpu with
applications to Voronoi diagram and distance trans-
form. In ACM Symp. Interactive 3D Graphics and
Games, pages 109–116.
Rosenfeld, A. and Pfalz, J. (1966). Sequential opera-
tions in digital picture processing. Journal of ACM,
13(4):471–494.
Satherly, R. and Jones, M. (2001). Vector-city vector dis-
tance transform. Computer Vision and Image Under-
standing, 82(3):238–254.
Sethian, J. (1996). A fast marching level set method for
monotonically advancing fronts. Nat’l Academy of
Sciences US-Paper Ed., 93(4):1591–1595.
Sigg, C., Peikert, R., and Gross., M. (2003). Signed dis-
tance transform using graphics hardware. In IEEE Vi-
sualization, pages 83–90.
Strzodka, R. and Telea, A. (2004). Generalized dis-
tance transforms and skeletons in graphics hardware.
In Joint EG/IEEE TVCG Symp. Visualization, pages
221–230.
Sud, A., Otaduy, M., and Manocha, D. (2004). DiFi: Fast
3D distance field computation using graphics hard-
ware. EG Computer Graphics Forum, 23(3):557–566.
Svensson, S. and Borgefors, G. (2002). Digital dis-
tance transforms in 3D images using information from
neighborhoods up to 5×5×5. Computer Vision and
Image Understanding, 88:24–53.
Telea, A. and van Wijk., J. (2002). An augmented fast
marching method for computing skeletons and center-
lines. In Symp. on Visualization, pages 251–260.
Tsitsiklis., N. (1995). Efficient algorithms for globally op-
timal trajectories. IEEE Trans. Automatic Control,
40(9):1528–1538.
Voronoi, G. (1908). Nouvelles applications des param`etres
continus `a la th´eorie des formes quadratiques.
deuxi´eme m´emoire: recherches sur les parall´elo`edres
primitifs. Reine Angewandte Mathematik, 134:198–
287.
VISAPP 2009 - International Conference on Computer Vision Theory and Applications
442