
IMPROVING 3D SHAPE RETRIEVAL WITH SVM
Elisabetta Delponte, Curzio Basso, Francesca Odone and Enrico Puppo
Department of Computer and Information Sciences - University of Genova, Via Dodecaneso 35, 16146 Genova, Italy
Keywords:
Shape retrieval, Statistical learning, Support Vector Machines.
Abstract:
In this paper we propose a technique that combines a classification method from the statistical learning lit-
erature with a conventional approach to shape retrieval. The idea that we pursue is to improve both results
and performance by filtering the database of shapes before retrieval with a shape classifier, which allows us to
keep only the shapes belonging to the classes most similar to the query shape. The experimental analysis that
we report shows that our approach improves the computational cost in the average case, and leads to better
results.
1 INTRODUCTION
Recent advances in 3D digitization techniques lead to
an increase of available 3D shapes datasets — see,
for instance, the Princeton dataset, the National Tai-
wan University database, or the data collected under
the EU funded project AIM@SHAPE
1
. In order to
be able to access such 3D shapes repositories, it may
be convenient to set up retrieval systems that support
the user in extracting from a potentially big repository
only the shapes that match a given specification.
In this paper we focus on the query by example
(QBE) approach, whereby retrieval is based on ap-
plying appropriate similarity measures to the shape
descriptors of the query example and all or some
shapes from the repository (also known as gallery
or dataset). Therefore, most research in this direc-
tion has focused on finding robust and discriminative
shape descriptors, on top of which applying rather
conventional similarity measures. Although efficient
indexing techniques may be adopted, it is easy to un-
derstand that this approach can suffer from the in-
crease of the number of shapes available in the repos-
itory and retrieval can easily fail.
We propose to adopt a combined strategy that cou-
ples conventional shape retrieval with classification
methods from the statistical learning literature, in or-
der to increase the retrieval efficiency and effective-
ness as the size of the shape repository grows. For
what concerns the classification algorithms to adopt,
1
http://shapes.aim-at-shape.net
we focus here on the well known Support Vector Ma-
chines (SVMs) (Vapnik, 1998). Different regularized
approaches, e.g. RLS (Rifkin et al., 2003) or iterative
methods (Lo Gerfo et al., 2008), could be applied as
well, at the price of some loss of performance.
Throughout the paper, we will point out how the
method that we propose is independent of the specific
choice of shape distribution and distance measure. In
this initial work, we will start off from a simple and
well known approach to shape retrieval (Osada et al.,
2002) and show that filtering the repository based on
classification can improve performance and results.
Since our method is completely independent of the
used descriptor, as long as it is a global vector with
fixed lenght, it will be easy in the future to employ
other shape descriptors, with better retrieval perfor-
mance.
More in details, let us assume that we have a
repository of labeled shapes divided in N classes, each
shape described by means of the D2 descriptor (Osada
et al., 2002). The key idea is to exploit a classification
tool to select a reduced number of classes more simi-
lar to a given query shape. After filtering out the less
relevant classes we perform a standard retrieval, based
on a similarity measure (the L
1
norm) computed just
for the shapes belonging to retained classes. We show
that this initial classification step improves both per-
formance and effectiveness of retrieval.
46
Delponte E., Basso C., Odone F. and Puppo E. (2009).
IMPROVING 3D SHAPE RETRIEVAL WITH SVM.
In Proceedings of the Fourth International Conference on Computer Graphics Theory and Applications, pages 46-51
DOI: 10.5220/0001755400460051
Copyright
c
SciTePress

2 BACKGROUND ON
STATISTICAL LEARNING
In this section we recall some basics of statisti-
cal learning that will be used throughout the pa-
per. Specifically we focus on penalized empirical risk
minimization approaches to supervised learning and,
implicitly, we refer to classification problems.
We first assume we are given two random vari-
ables x ∈ X ⊆ R
d
(input) and y ∈ Y ⊆ R (out-
put). In the binary classification case, the elements
x ∈ X are feature vectors (e.g., shape descriptors),
while y ∈ {−1, 1}. We then consider a set of data
S = {(x
i
,y
i
)|1 ≤ i ≤ n} that we call a training set ob-
tained by randomly sampling the set X ×Y .
Supervised learning approaches use the training
set to learn a function f : X → Y that can be applied
to previously unseen data. Indeed, we say that an al-
gorithm is predictive or that it has good generaliza-
tion properties if it applies successfully to data other
than training examples. A large class of algorithms
are based on the minimization of the penalized em-
pirical risk in a given space of functions H :
min
f ∈H
1
n
n
∑
i=1
V (y
i
, f (x
i
)) + λJ[ f ]
where V is some loss function measuring the solu-
tion’s goodness of fit, J[ f ] is a functional of the func-
tion f penalizing complexity, and λ is a regulariza-
tion parameter that trades off between the two terms.
Within this framework we will refer in particular to
the so-called Tikhonov regularization, using a L
2
-
norm in H as a penalization term:
min
f ∈H
1
n
∑
V (y, f (x
i
)) + λ|| f ||
2
H
.
As for the choice of H , a very useful class of
spaces to enclose some notion of smoothness in their
norm are the Reproducing Kernel Hilbert Spaces
(RKHS). It can be shown that for every RKHS there
exists a corresponding unique positive-definite func-
tion K that we call a kernel function. Conversely, for
each positive-definite function K on X × X there is
a unique RKHS H that has K as a reproducing ker-
nel. A very important theorem in statistical learning
is the representer theorem stating that, under general
conditions on the loss function V , the minimizer of a
Tikhonov regularization problem in a RKHS associ-
ated to a kernel K is of the form
f (x) =
n
∑
i=1
c
i
K(x
i
,x) (1)
for some (c
1
,... ,c
n
) ∈ R
n
.
Roughly speaking, the kernel function K can be
expressed as a dot product in a higher dimensional
space. Choosing a kernel or, equivalently, choosing a
hypothesis space, allows us to formalize a non-linear
problem by mapping the original observations (fea-
ture vectors in the input space) in a different space
where a linear algorithm may be applied. Thanks to
the kernel, the mapping may be performed implicitly
with the so-called kernel trick:
K(x
1
,x
2
) = φ(x
1
) · φ(x
2
)
This makes a linear classification in the new space
equivalent to non-linear classification in the origi-
nal space. In this work we use Gaussian kernels,
K(x
i
,x
j
) = exp(−||x
i
− x
j
||
2
/2σ
2
). The parameter σ
is the width of the kernel and needs to be tuned ap-
propriately. Its choice is somehow alternative to the
choice of λ: a small σ may lead to overfitting, a big σ
to oversmoothing.
The choice of the loss function leads to different
learning algorithms. The L
2
-norm leads to Regular-
ized Least Squares (RLS) algorithms (Caponnetto and
De Vito, 2006), while the so-called Hinge loss (1 −
y f (x))
+
leads to Support Vector Machines (SVM)
(Vapnik, 1998). SVMs have been used with success in
a number of different application domains. They are
characterized by many nice properties, some of which
are not apparent from the regularized formulation fol-
lowed in this section. We mention here, as it will be
useful later in the paper, the fact that they produce a
sparse solution on the set of input data. This means
that the solution (c
1
,. .. ,c
n
) they produce will usually
contain few non-zero entries. The training data asso-
ciated to non-zero weights are referred to as support
vectors. For a geometric intuition of such a property
the reader is referred to (Vapnik, 1998).
3 RELATED WORK
The problem of retrieval and matching of shapes has
been extensively studied in numerous fields such as
computer vision, computer graphics and molecular
biology.
Most approaches to shape retrieval are based on
shape descriptors and exhaustive search. A shape de-
scriptor is computed for each object in a database, as
well as for the query object. Then the descriptor of
the query object is compared with all descriptors of
objects in the database through some measure for pat-
tern matching, and a ranked list of most similar ob-
jects is retrieved.
A large class of works deal with global descriptors
in the form of feature vectors, i.e., arrays of scalar
IMPROVING 3D SHAPE RETRIEVAL WITH SVM
47

values computed by some analysis of the 3D shape.
Some of such feature vectors are in fact histograms
of either scalar fields computed on the shape, or some
form of shape distribution. The D2 shape distribution
histogram (Osada et al., 2002) that we adopt here, is
one of the simplest descriptors to compute. More re-
cent descriptors exhibit better performances though.
As already remarked, the scope of this work is some-
how orthogonal to the descriptor adopted, as long as
this falls in the class of feature vectors, so our ap-
proach could (and will) be adopted also with other
descriptors. Other works use descriptor based on lo-
cal features and more complex matching procedures.
A few approaches to 3D object retrieval based on
statistical learning have been proposed in the litera-
ture. In their seminal work, Elad, Tal and Ar (Elad
et al., 2001) proposed a semi-interactive retrieval sys-
tem based on a feature vector descriptor and on the
use of SVM together with relevance feedback. In
(Leifman et al., 2005) the relevance feedback mech-
anism is combined with discriminant analysis tech-
niques to achieve a reduction of the dimensionality
of the feature vectors. Different methods based on
relevance feedback were compared by Novotni et al.
(Novotni et al., 2005) and those based on SVM were
found to give better performances. Relevance feed-
back on SVM was also adopted in a more recent work
by Leng, Qin and Li (Leng et al., 2007), where the
authors adopt an algorithm for SVM active learning,
previously proposed for image retrieval.
Hou, Lou and Ramani (Hou et al., 2005) use SVM
for organizing a database of shapes through clustering
and then to perform the classification and retrieval. In
(Xu and Li, 2007) the authors, assuming a training
set structured in N classes, employ a similarity mea-
sure including a term depending on the ranked out-
put of N one-vs-all classifiers. Shape classification
has also been addressed by Barutcouglu and De Coro
(Barutcuoglu and DeCoro, 2006) by using a Bayesian
approach to exploit the dependence between classes,
assuming that they are organized in a hierarchical
fashion. However, their work is focused only on the
classification problem, and retrieval is not addressed.
A peculiarity of kernel methods is that they allow
for the design of ad hoc kernels able to capture the ex-
pressiveness of feature vectors. A number of kernels
for different application domains have been proposed
in the literature (Taylor and Cristianini, 2004). For in-
stance, a possible way to deal with histogram-like de-
scriptions is to treat them as probability distributions
and to resort to kernels defined on probability mea-
sures (Jebara et al., 2004). Alternatively, kernel func-
tions derived from signal or image processing may be
adopted – see, for instance, (Odone et al., 2005).
All methods above feed the classification algo-
rithms with shape descriptors of a unique type. In
(Akgul et al., 2008) the authors proposed a fusion al-
gorithm, based on the so-called empirical ranking risk
minimization, which combines different descriptors.
The algorithm can also be implemented via SVMs.
The learning algorithm returns the weights to asso-
ciate to the various descriptors. After this, conven-
tional retrieval may be performed, for instance by
means of relevance feedback.
4 OUR APPROACH
We propose a technique that is a combination of clas-
sical retrieval methods with a classification approach
typical of the learning-from-examples framework.
We assume that our repository of shapes is labeled
and that, for simplicity, a unique label is assigned to
each shape. We can thus organize our repository in
classes using the labels to build a dataset per each
class. The idea that we pursue is to reduce complexity
of search by filtering the available repository before
retrieval, i.e., by using only shapes belonging to the k
most relevant classes to the query object.
As a benchmark method, we consider a popular
work proposed by Osada et al., based on statistical
shape descriptors (Osada et al., 2002): the shape dis-
tribution of each 3D model is represented by its D2
descriptor, which consists of a histograms of the dis-
tances between pairs of vertices randomly selected on
the shape surface; two descriptors are compared with
the L1 distance. For a given query object, its descrip-
tor is compared with all the descriptors available on
the database, and the output returned by the retrieval
system is a ranked list of the n most similar shapes.
In this paper, we adopt the same shape descriptor
and we follow a similar pipeline. Our variation of the
original pipeline consists of performing shape classi-
fication prior to shape retrieval, in order to reduce the
size of the repository of shapes to be analyzed.
The reminder of the section describes the de-
tails of the classification (filtering) procedure and dis-
cusses the computational advantages of our choice.
Then we evaluate the appropriateness of our choice in
terms of nearest-neighbor performance and retrieval
indicators (the so-called first tier and second tier).
4.1 Classification and Retrieval
Let us assume we start from a shape repository con-
taining M labeled shapes, belonging to N different
classes. Each class is composed of a number of shapes
that could be arbitrarily different.
GRAPP 2009 - International Conference on Computer Graphics Theory and Applications
48

We aim at designing a shape classifier that returns
the shape classes
ˆ
S = {S
1
,. .. ,S
k
} most similar to a
query object. This will allow us to restrict retrieval to
the shapes belonging to set
ˆ
S.
The shape classification problem that we consider
is a multi-class classification problem. We adopt a
one-vs-all procedure that requires we train N binary
classifiers of the type class C
i
, with i = 1, .. ., N, ver-
sus all the other classes – see, e.g., (Bishop, 2006).
Thus, for each class we train a classifier: each
training set is made of an equal number of positive
and negative examples of the shapes, where the nega-
tive examples are extracted from all the other classes
of the repository.
In this work we adopt Support Vector Machines
(SVM) (Vapnik, 1998) with Gaussian kernels as a
classification algorithm. Our choice is mainly moti-
vated by performance reasons, in particular the fact
that the solution of a SVM classifier is sparse on
the training data, but other binary classifiers could be
used within the same pipeline. In practice, we use the
SVM implementation of SV M
light
(Joachims, 1999).
The optimal values for the two free parameters,
i.e. the width σ of the Gaussian kernel and the
SVM regularization parameter, are set with a stan-
dard leave-one-out (LOO) procedure (see for instance
(Bishop, 2006)).
At run time, we apply a query object to each clas-
sifier available and we rank the output of the classi-
fication results, thus obtaining a list of classes sorted
from the most similar to the least similar to a given
query.
We exploit this result to filter shapes available
in the repository before we apply a standard nearest
neighbor (NN) retrieval. In other words, given a query
example, we test it against the N classifiers, rank the
results and then keep the shapes belonging to the first
k classes for the following retrieval process.
Notice how the choice of an appropriate k is cru-
cial both for computational and performance reasons.
A small k will make the retrieval very fast but it may
impoverish the results. A big k (k → N) would in-
crease retrieval time yet not necessarily improve per-
formance - see the discussion in Section 5.
4.2 Computational Advantages
The computational cost of shape filtering followed by
a retrieval restricted on the filtered classes is equal to
the maximum cost between the two operations.
Note that if the classification method is not sparse,
there is no computational advantage. Indeed, if the
filtering procedure has to evaluate the basis K(x
i
,x)
in Eq. (1) for all training shapes x
i
, then the fil-
tering phase is more costly than actual retrieval, no
matter the choice of k. For instance, if we consider
a Regularized Least Squares (RLS) (Caponnetto and
De Vito, 2006) approach, the query shape x is com-
pared with each training shape x
i
via a kernel function
K, then for each class C we have a summation over all
the training data in it (see Eq. (1)).
In the case of SVM, instead, the sparsity on the
training data in the obtained solution means that filter-
ing requires fewer comparisons - one per each support
vector - since in this case the summation runs on the
support vectors only. There is no way to evaluate a
priori the number of obtained support vectors, as they
depend on the training set (both their cardinality and
the data representation chosen) and on the choice of
the kernel function. In the average case, and assum-
ing an appropriate choice of the representation and
the kernel function, we observed a saving in terms of
number of comparisons between the query object and
training data. This effect becomes more relevant as
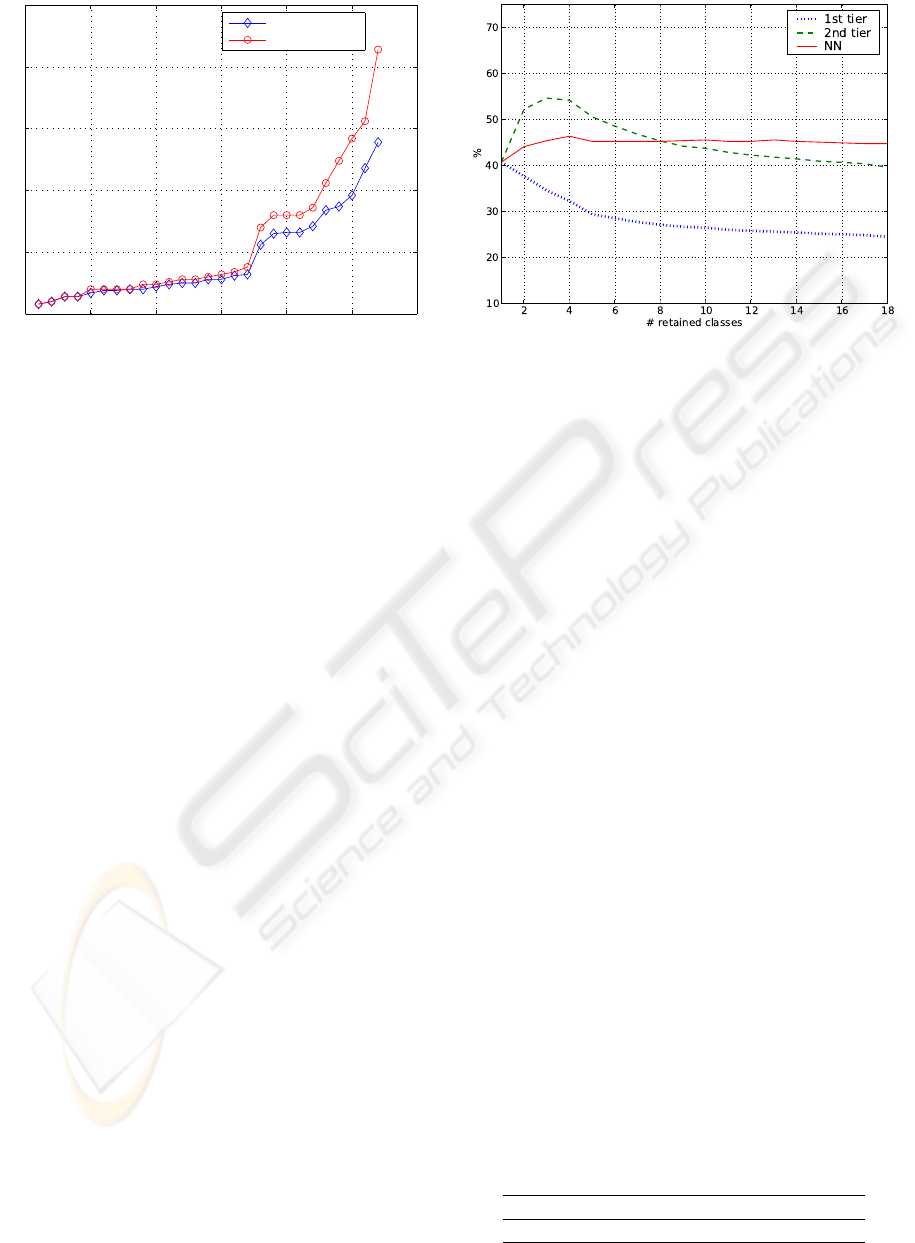
the training set size grows (see Section 5 and Figure
1).
5 EXPERIMENTAL RESULTS
In this section we show the results of retrieval made
on a subset of the Princeton Shape Benchmark (PSB)
repository (Shilane et al., 2004) and we compare our
results with the ones reported in (Osada et al., 2002).
The PSB is a publicly-available database of 3D
models, widely adopted by the shape retrieval com-
munity. The repository contains 1814 polygonal mod-
els classified by humans with respect to function and
form in 27 classes. For our experiments we chose
a subset of 18 PSB classes, that fulfill requirements
of intra-class shape homogeneity and a threshold for
cardinality (we keep only classes with at least 10 ele-
ments on the training and on the test set).
To evaluate the performances of the retrieval we
use the following evaluation methods:
Nearest Neighbor (NN) : the percentage of closest
matches that belong to the same class as the query.
First Tier (I-T) : the percentage of models in the
query’s class that appear within the top k matches
where k is the size of the query’s class.
Second Tier (II-T) : the percentage of models in
the query’s class that appear within the top 2k
matches where k is the size of the query’s class.
The means shown in Figure 2 and Table 1 are
weighted with respect to the size of the test set.
We trained 18 SVM classifiers according to the
previously described procedure. After a preliminary
IMPROVING 3D SHAPE RETRIEVAL WITH SVM
49
0 5 10 15 20 25 30
0
50
100
150
200
250
classes
# support vectors
# training data
Figure 1: Comparison between the original size of the train-
ing sets and the number support vectors for the 18 classes
considered; the sparsity of the solution is more noticeable
for repositories with more than 20 entries.
analysis on the performance of different standard ker-
nels, we adopted a Gaussian kernel. Because of the
presence of very small classes, we adopted a LOO
procedure to select the regularization parameter and
the parameter σ of the Gaussian kernel. Figure 1
shows how the number of support vectors becomes
significantly smaller than the training set size when
the latter grows. This is an advantage, suggesting that
if we adopt SVMs the sparsity of the solution with
respect to the training data may reflect on an overall
computational saving. However, the dataset consid-
ered in our experiments is too small to allow for an
exhaustive analysis. At run time, we test all the query
shapes against the 18 classifiers.
As we pointed out previously in the paper, the
choice of the number of classes to keep for shape
retrieval is crucial and there is no obvious common
sense rule to apply. Obviously the presence of the
right class in the reduced set of shapes does not guar-
antee a successful retrieval, but its absence means
that the retrieved elements will all be wrong. At the
same time we notice how, as the size of the reposi-
tory grows, the average performance of the retrieval
indicators degrade. Fig. 2 shows how they vary as
the number of retained classes grow. From this analy-
sis we conclude that a small number of classes ([2-5])
should be kept both for efficiency and performance
reasons. The remaining experiments are performed
with k = 4.
By analysing the performance for the different
classes it is possible to notice that the performances
of direct retrieval are comparable or above our filter-
ing method for those classes which have very small
training sets (less than 10 elements), while SVM fil-
Figure 2: Dependence of retrieval performance on the num-
ber k of retained classes grows. The three lines show the
metrics we used: 1st tier, 2nd tier and nearest neighbor.
tering is a clear advantage when the training set has
more than 40 elements.
Table 1 reports the average retrieval results over
all the classes, in the case of direct retrieval and SVM
filtering with k = 4. Notice that direct retrieval repre-
sents the results obtained with the original work by
Osada et al. (Osada et al., 2002) on our datasets.
The advantage of our approach is evident. The results
presented in the original work (Osada et al., 2002)
are relative to a different (and smaller) repository and
the performances are described with different indica-
tors, therefore comparison is more complex. We con-
clude reporting that in (Gal et al., 2007) the follow-
ing results, obtained with Osada approach on a dif-
ferent subset of the PSB, are reported: I − T = 33%,
II −T = 47%, NN = 59%. The NN result seems to be
superior to the one we obtain, the reasons may be due
to the different characteristics of the selected classes
and to the fact that apparently only stable subsets of
shapes per each class are kept.
6 CONCLUSIONS
We have proposed a method based on SVM for filter-
ing the relevant classes in a 3D object database prior
to shape retrieval. SVM classifiers are built for all
classes of object in a database, and just the k most rel-
Table 1: Results with our approach (retaining 4 classes)
and our implementation of (Osada et al., 2002).
I-T II-T NN
SVM filtering 33% 55% 47%
(Osada et al., 2002) 24% 39% 44%
GRAPP 2009 - International Conference on Computer Graphics Theory and Applications
50

evant classes or a query object are searched to answer
a query by similarity. We have shown that not only
our method can improve performance by pruning the
repository to be searched, but results are better with
respect to those obtained with exhaustive search, us-
ing the same shape descriptor.
The shape descriptor used in this initial work is
outperformed by others at the state-of-the-art. There-
fore, we plan to test our approach also with other, bet-
ter performing, descriptors. As already mentioned,
our filtering is somehow orthogonal with respect to
the descriptor used. However, the quality of a descrip-
tor may also influence the performance of classifica-
tion through SVM. If some other descriptor could give
us a better performance in classification, we could re-
strict search to an even smaller number k of classes,
thus improving performance further.
ACKNOWLEDGEMENTS
The work is supported by the PRIN project 3SHIRT
(3-dimensional Shape Indexing and Retrieval Tech-
niques) funded by the Italian Ministry of Research
and Education.
REFERENCES
Akgul, C. B., Sankur, B., Yemez, Y., and Schmitt, F. (2008).
Similarity score fusion by ranking risk minimization
for 3d object retrieval. In Eurographics workshop on
3D object retrieval.
Barutcuoglu, Z. and DeCoro, C. (2006). Hierarchical shape
classification using bayesian aggregation. In SMI ’06:
Proceedings of the IEEE International Conference
on Shape Modeling and Applications 2006, page 44,
Washington, DC, USA. IEEE Computer Society.
Bishop, C. (2006). Pattern Recognition and Machine
Learning. Springer.
Caponnetto, A. and De Vito, E. (2006). Optimal rates for
regularized least-squares algorithm. Found. Comput.
Math. In Press, DOI 10.1007/s10208-006-0196-8,
Online August 2006.
Elad, M., Tal, A., and Ar, S. (2001). Content based retrieval
of vrml objects: an iterative and interactive approach.
In Proceedings of the sixth Eurographics workshop
on Multimedia 2001, pages 107–118, New York, NY,
USA. Springer-Verlag New York, Inc.
Gal, R., Shamir, A., and Cohen-Or, D. (2007). Pose-
oblivious shape signature. IEEE Transactions on Vi-
sualization and Computer Graphics, 13(2):261–271.
Hou, S., Lou, K., and Ramani, K. (2005). SVM-
based semantic clustering and retrieval of a 3d model
database. Computer Aided Design and Applications,
2(1-4):155–164.
Jebara, T., Kondor, R. I., and Howard, A. (2004). Proba-
bility product kernels. Journal of Machine Learning
Research, 5:819–844.
Joachims, T. (1999). Making large-scale svm learning prac-
tical.
Leifman, G., Meir, R., and Tal, A. (2005). Semantic-
oriented 3d shape retrieval using relevance feedback.
The Visual Computer.
Leng, B., Qin, Z., and Li, L. (2007). Support vector ma-
chine active learning for 3d model retrieval. Journal of
Zhejiang University SCIENCE A, 8(12):1953–1961.
Lo Gerfo, L., Rosasco, L., Odone, F., De Vito, E., and Verri,
A. (2008). Spectral algorithms for supervised learn-
ing. Neural Computation, 20:1873–1897.
Novotni, M., Park, G., Wessel, R., and Klein, R. (2005).
Evaluation of kernel based methods for relevance
feedback in 3d shape retrieval. In Proceedings 4th
Int. Workshop on Content-based Multimedia Indexing,
Riga, Latvia.
Odone, F., Barla, A., and Verri, A. (2005). Building ker-
nels from binary strings for image matching. IEEE
Transactions on Image Processing, 14(2):169–180.
Osada, R., Funkhouser, T., Chazelle, B., and Dobkin, D.
(2002). Shape distributions. ACM Trans. Graph.,
21(4):807–832.
Rifkin, R., Yeo, G., and Poggio, T. (2003). Regularized
least-squares classification.
Shilane, P., Min, P., Kazhdan, M., and Funkhouser, T.
(2004). The princeton shape benchmark. In SMI
’04: Proceedings of the Shape Modeling International
2004, pages 167–178, Washington, DC, USA. IEEE
Computer Society.
Taylor, J. S. and Cristianini, N. (2004). Kernel Methods for
Pattern Analysis. Cambridge University Press.
Vapnik, V. (1998). Statistical learning theory. Adaptive and
learning system for signal processing, communication
and control. John Wiley and Sons Inc.
Xu, D. and Li, H. (2007). 3D shape retrieval integrated
with classification information. In Proceedings of
the Fourth International Conference on Image and
Graphics, pages 774–779, Washington, DC, USA.
IEEE Computer Society.
IMPROVING 3D SHAPE RETRIEVAL WITH SVM
51
