
IMAGE CODING WITH CONTOURLET/WAVELET
TRANSFORMS AND SPIHT ALGORITHM
An Experimental Study
Sławomir Nowak and Przemysław Głomb
Institute of Theoretical and Applied Informatics, Polish Academy of Science, Bałtycka 5, Gliwice, Poland
Keywords: Contourlet transform, Wavelet transform, SPIHT algorithm, Image coding, Transmission errors.
Abstract: We investigate the error resilience of the image coded with the wavelet/contourlet transform and the SPIHT
algorithm. We experimentally verify the behaviour for two scenarios: partial decoding (as with scalable
coding/transmission) and random sequence errors (as with transmission errors). Using a number of image
quality metrics, we analyze the overall performance, as well as differences between each transform. We
observe that error difference between transforms varies with length of decoded sequence.
1 INTRODUCTION
Image coding theory forms a foundation of today's
multimedia technologies: internet web pages, digital
cameras, medical diagnostics to name a few. The
objective of image coding is to reduce the
transmission/storage requirements, by exploiting
statistical structure of images and human visual
perception properties.
Current paradigm for image compression
involves using a transform for recoding pixel data,
then bit packing of the coefficients' data into a coded
bitstream. A JPEG – 2000 standard (JPEG, 2000), is
a practical formalization, focusing on wavelet
transform and EBCOT (embedded block coding
with optimized truncation) bit ordering algorithm.
Other bit ordering algorithms have also been
proposed, most notably SPIHT (set partitioning in
hierarchical trees), described in (Said and Pearlman,
1996). Recently, an alternative to wavelet transform
has been suggested, in the form of contourlet
transform (Do and Vetterli, 2005), which has better
property of representing directional image
information, an important requirement for image
coding applications.
In many applications we expect the image to be
reconstructed from the coded bitstream with errors,
which can result either from the coding system
(lossy compression) or transmission medium
(packet loss or errors). The former is analyzed as
rate-distortion theory, and focuses on relation of
bitstream length to image quality (with respect to
some predefined metric). The latter is studied by
observing distortion introduced by errors in coded
bitstream. While there are methods that improve
resilience of the bitstream, i.e. using error
correcting codes (Kim et al, 2004), or post-process
the image to conceal/remove errors (Kung et al,
2006), the quantitative and qualitative analysis of
coding system errors of both types is the key issue
in design of a compression system.
While the statistical analysis of the contourlet
transform indeed suggests it is better in
representing image information (Po and Do, 2006),
and thus possibly better suited for image coding
systems, the exact gain of using it in place of
wavelet transform is still an open issue. (Belbachir
and Goebel, 2005) present a straightforward
approach to compress images with contourlets, but
provide only brief results with limited error
discussion. (Esakkirajan et al, 2006) give a more
detailed analysis including different filters and
wavelet to contourlet comparisons. Their approach
(multistage vector quantization) is not suitable for
analysis scalability errors; they also don't
investigate error resilience. They report small gain
for contourlet transform. (Eslami and Radha, 2004)
focus on combining contourlets after wavelets with
SPIHT coding. They report better results with their
approach than with wavelets alone. (Liu and Liu,
2006) also focus on combination of wavelets and
contourlets in sophisticated scheme. They report
improved performance of contourlet over wavelet,
37
Nowak S. and Głomb P. (2009).
IMAGE CODING WITH CONTOURLET/WAVELET TRANSFORMS AND SPIHT ALGORITHM - An Experimental Study .
In Proceedings of the First International Conference on Computer Imaging Theory and Applications, pages 37-42
DOI: 10.5220/0001767400370042
Copyright
c
SciTePress

with their scheme providing additional gains. The
results are provided for selected bit rates.
Our experiments were motivated by the need for
more throughout, than reported above, evaluation of
practical difference of coding with wavelets and
contourlets. The objectives were defined as:
compare wavelets and contourlets side by
side, as much as possible;
provide detailed analysis of scalability, in the
form of partial reconstruction of the coded
stream;
provide analysis of bit stream perturbations
(consistent with network errors, i.e. streaming
in wireless network);
use a range of error metrics, for qualitative
evaluation of introduced errors.
Our findings are:
the wavelet-SPIHT method works better when
the near-lossless operations are demanded
(smaller sequences sizes), whereas when a
given level of quality loss is acceptable, the
contourlet method gives better image quality
for smaller sequence size;
it is possible to parameterize the SPIHT algorithm
to obtain images at definite quality level;
when certain level of image quality loss is
accepted, some subsequences (refinement
parts) of the output sequence can be treated as
low-priority data.
This work is organized as follows: second
section presents our approach and experimental
framework, third section presents experiment results,
last section presents conclusions.
2 THE METHOD
We investigate a coding systems consisting of two
elements: image transform and bit coder. For
transform, we use interchangeably wavelet
transform (implemented as standard 9/7 filter bank,
as in (JPEG, 2000)) and contourlet transform
(implemented with surfacelet transform, using (Lu
and Do, 2007)). For bit coding, we use SPIHT
algorithm (Said and Pearlman, 1996). The usage is
motivated by good results reported, but also by
difficulties with extending other algorithms, like
EBCOT, to contourlets (Głomb et al, 2007). The
implementation was done in C++.
We use a number of metrics to measure image
distortion. Mean square error (MSE) and Peak signal
to noise ratio (PSNR) are defined as:
M
SE
k
PSNR
2
10
log10=
(1)
where:
∑∑
==
−
⋅
=
N
i
M
j
jifjif
MN
MSE
11
2'
))],(),(([
1
(2)
k – number of image colors minus 1;
N,M – sizes of image;
f(i,j) – input image;
f
’
(i,j) – output image.
We also use average per pixel error (denoted
PERPX), and measures related to edge degradation.
The latter are included as it has been observed (Al-
Otum, 1998) that edge degradation in video coding
is an important component of human quality
perception. For measurement of the latter, we first
use a Sobel edge operator for reference and distorted
image, then measure MSE and NCC (normalized
cross correlation) of the edge images.
The aim of work was to evaluate the image
quality as a function of decoded sequence size and to
determine the resistance of the output, linear
sequence to errors.
3 EXPERIMENTAL RESULTS
Within the experiments we use the typical set of
images (Baboon, Barbara, Boat, Goldhill, Lena,
Peppers), universally used in digital images studies.
3.1 Image Quality as a Function of the
Decoded Sequence Size
The SPIHT algorithm codes more important
coefficient bits first. While decoding, image quality
increases progressively. Because of this, the graph of
image quality as a function of the size of decoded
sequence is nonlinear.
During experiments the process of decoding
output sequence was being stopped at specific point,
expressed in percent of the whole sequence size. The
single steep was 2[%].
By comparing output images to the original ones,
the qualities of output images were evaluated and
the graph of image quality was obtained. Each graph
expresses the average results of each measurement
method for the whole set of images.
The size of output sequences for contourlet and
wavelet decompositions were different. The sizes for
contourlet method sequences are considerably
larger. We calculated the value γ (3).
IMAGAPP 2009 - International Conference on Imaging Theory and Applications
38
68,2
...
...
==
methwaveletforseqofsizeavrg
methconturletforseqofsizeavrg
γ
(3)
In order to compare both methods we place
contourlet and wavelet methods’ graphs together on
each chart. 100[%] on X axis means 100[%] of
a wavelet sequence and 100/γ = 100/2,68 = 37,3[%]
of a contourlet sequence. Results are presented on
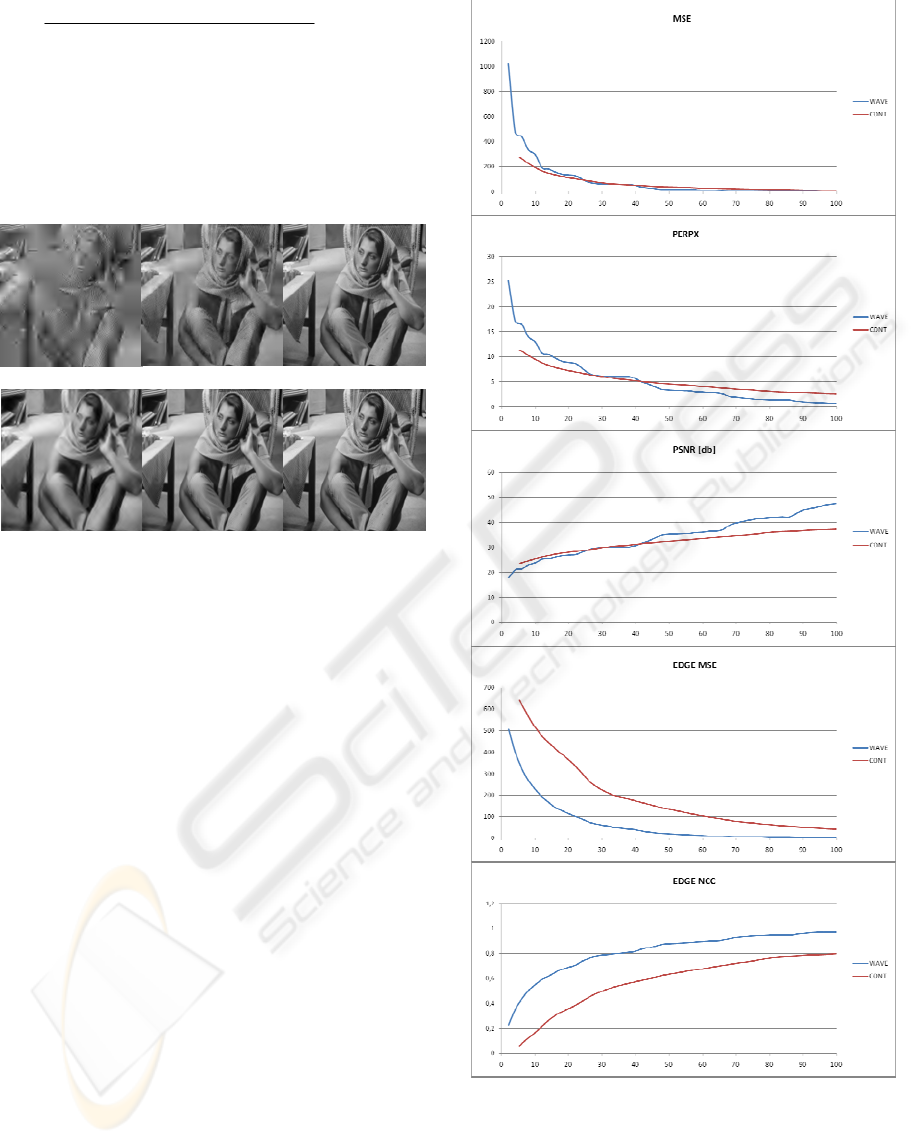
Figure 2. Sample images are presented on Figure 1.
Figure 1: Sample images (Barbara.jpg) for conturlet and
wavelet methods, after decoding 2[%], 20[%], 50[%] of
the output SPIHT sequence.
3.1.1 Discussion
Presented results let us evaluate the methods and
make a preliminary classification.
The wavelet decomposition together with the
SPIHT algorithm generates smaller sizes of
sequences, in compare to the contourlet ones (by
average factor γ). So, in potential application, when
the lossless transmissions are demanded, the wavelet
method seems to be a better way. But in some cases,
when a given level of quality loss is acceptable, the
contourlet method gives better image quality for
smaller sequence size. One can observe that on
Figure 1, where for MSE, PERPX, PSNR graphs the
distinct cross point occurred. It is also evident, while
comparing images presented on Figure 1.
Results can be useful in case of the
parameterization of the SPIHT algorithm. Based on
the results, approximation function of quality from
the length of sequence, can be calculated and
sequences coding images on definite quality can be
obtained. Examples of the approximation functions
(fitting the EDGE NCC metrics) are presented on
Figure 3.
Figure 2: Image quality as a function of the decoded
sequence size for contourlet and wavelet methods.
3.2 Image Quality as a Function of
Distortions
The SPIHT generates two types of data. The first
Barbara.jpg, Wavelet method
2[%] 20[%] 50[%]
Barbara.jpg, Conturlet method
2[%] 20[%] 50[%]
IMAGE CODING WITH CONTOURLET/WAVELET TRANSFORMS AND SPIHT ALGORITHM - An Experimental
Study
39

Figure 3: Approximation functions of the EDGE NCC
metric for contourlet and wavelet methods.
comes from the process of hierarchical tree
creation. The second consists of refinement bits.
The output sequence alternately consists of “tree
creation bits” subsequences and “refinement bits”
subsequences.
Loss or error affected by any bit in “tree creation
bits” subsequence makes the further process of
decoding impossible, because the algorithm loses the
correct path through binary trees. Considering e.g.
network streaming, the “tree creation bits”
subsequences need error protection.
The “refinement bits” subsequences affect only
for single pixels and do not need special protection.
After loss or error affected by single bits or even the
whole subsequences, the process of decoding can be
continued. Occurrences of errors within the
subsequence influences to a little degree on the
image quality.
When considering errors within “refinement bits”
subsequences it is important to mention, that the
original size of each subsequence have to be preserved.
In the opposite case the algorithm also loses the correct
path through subsequent stages. We consider rather
errors then a loss of data.
Introducing distortions to the “refinement bits”
subsequences, the graph of image quality as
a function of simplified model of error level is
obtained. During the experiments the probability of
distortion of individual bits varied from 0[%] (no
distortions) to 100[%] (every bit was distorted, and
as a consequence the “refinement bits” subsequences
changed to the inverted form of the original).
As in the previous experiments, the contourlet
and wavelet methods are compared. The qualities
of output images were evaluated and the graph of
image quality (average results) was obtained. To
compare results in direct way the γ value was used.
Results are presented on Figure 4 and sample
images are presented on Figure 5.
Figure 4: Image quality as a function of distortion
probability of individual bits in “refinement bits”
sequence.
3.2.1 Discussion
Obtained results show that bits within the
“refinement bits” subsequences have little influence
on image quality. The “refinement bits”
subsequences constitute average about 33[%] or the
SPIHT output sequence size for contourlet
decomposition method and about 28[%] for wavelet
decomposition method.
Considering transmission of images via network
using dedicated protocols, when certain level of
image quality loss is accepted, one can treat
IMAGAPP 2009 - International Conference on Imaging Theory and Applications
40

Figure 5: Sample images (Barbara.jpg) for conturlet and
wavelet methods, different probability of distortion of
individual “refinement bits” in sequence.
“refinement bits” subsequences as low-priority data.
In case of a transmission error (individual bits
distortion or even whole block loss) retransmission
of data is not necessary. In certain cases, it is
possible to omit completely the “refinement bits”
subsequences. Only the size of “refinement bits”
subsequence have to be retained.
Replacements for it, the additional, excessive
data can be introduced to the “tree creation bits”
subsequences, which are necessary to follow the
SPIHT algorithm.
4 CONCLUSIONS
The main goal of the work was to compare two
methods of decomposition: contourlet and wavelet
in employment with the SPIHT algorithm and to
investigate their properties. The comparison can be
helpful when new protocols for image transmission
are designed, especially when a network streaming
through noisy environment is considered.
The conclusions are:
The wavelet-SPIHT method generates smaller
sizes (by average factor γ = 2,68) of
sequences, but the contourlet-SPIHT method
gives better image quality for smaller
sequence size (it should be noted that there are
algorithms producing contourlet
decomposition with less redundancy);
It is possible to parameterize the SPIHT
algorithm to obtain sequences coding images
at definite level of quality;
The “refinement bits” subsequences can be
treated as low-priority data. Bits within that
subsequences have little influence on image
quality.
An important observation noted during our
experiments is that while several studies report
contourlet transform to be generally superior to
wavelet transform, we report that the gain is closely
related to image structure. Thus, in general one can
expect a considerable variation of differences
between the transforms depending on image source.
ACKNOWLEDGEMENTS
This work was supported by the Polish Ministry of
Science and Higher Education research project
3 T11C 045 30 “Application of contourlet transform
for coding and transmission stereo-images”.
REFERENCES
Al-Otum, H.M., 1998. "Evaluation of reconstruction
quality in image vector quantization using existing and
new measures", In proc. IEEE Vis. Image Signal
Processing, vol. 145, no. 5, pp. 349-356.
Belbachir, A.N, Goebel, P.M., 2005. "The contourlet
transform for image compression", In Proc. of Physics
in Signal and Image Processing.
Do, M.N. Vetterli, M. 2005. "The contourlet transform: an
efficient directional multiresolution image
representation", IEEE Transactions Image on
Processing, vol. 14, no. 12, pp. 2091-2106.
Esakkirajan, S., Veerakumar, T., Murugan, V.S.,
Sudhakar, R., 2006. "Image compression using
contourlet transform and multistage vector
quantization", ICGST International Journal on
Graphics, Vision and Image Processing (GVIP), vol.
6, no. 1, pp. 19–28.
Eslami, R, Radha, H, 2004. "Wavelet-based contourlet
coding using an SPIHT-like algorithm", In Proc. of
Conference on Information Sciences and Systems, pp.
784–788.
Głomb, P., Puchała, Z., Sochan, A., 2007. "Context
selection for efficient bit modeling of contourlet
Barbara.jpg, Wavelet method
2[%] 20[%] 40[%]
60[%] 80[%] 100[%]
Barbara.jpg, Conturlet method
2[%] 20[%] 40[%]
60[%] 80[%] 100[%]
IMAGE CODING WITH CONTOURLET/WAVELET TRANSFORMS AND SPIHT ALGORITHM - An Experimental
Study
41

transform coefficients", Theoretical and Applied
Informatics, vol. 19, No. 2, pp. 135-146.
JPEG, 2000. International Standard ISO/IEC 15444-1
"Information technology – JPEG 2000 image coding
system: Core coding system".
Kim, J., Mersereau, R.M., Altunbasak, Y., 2004. "A
Multiple-Substream Unequal Error-Protection and
Error-Concealment Algorithm for SPIHT-Coded
Video Bitstreams", IEEE Transactions Image on
Processing, vol. 13, no. 12, pp. 1574.
Kung, W.-Y., Kim, C.-S., Kuo, C.-C.J., 2006. "Spatial and
Temporal Error Concealment Techniques for Video
Transmission Over Noisy Channels", IEEE
Transactions on Circuits and Systems for Video
Technology, vol. 16, no. 7, pp. 789-803.
Liu, F., Liu, Y., 2006. "Multilayered contourlet based
image compression", In Advances in Multimedia
Modeling 2006 (Lecture Notes in Computer Science
vol. 4351), pp. 299-308.
Lu, Y.M., Do, M.N., 2007. "Multidimensional Directional
Filter Banks and Surfacelets", IEEE Transactions on
Image Processing, vol. 16, no. 4, pp. 918-931.
Po, D.D.-Y., Do, M.N., 2006. "Directional multiscale
modeling of images using the contourlet transform",
IEEE Transactions Image on Processing, vol. 15, no.
6, pp. 1610-1620.
Said, A., Pearlman, W.A. 1996. "A New Fast and Efficient
Image Codec Based on Set Partitioning in Hierarchical
Trees", IEEE Transactions on Circuits and Systems
for Video Technology, vol. 6, pp. 243-250.
IMAGAPP 2009 - International Conference on Imaging Theory and Applications
42
