A SOLID TEXTURE DATABASE FOR SEGMENTATION

AND CLASSIFICATION EXPERIMENTS

Ludovic Paulhac, Pascal Makris and Jean-Yves Ramel

Université François Rabelais Tours, Laboratoire Informatique (EA 2101), France

Keywords:

Solid texture database, Image classiﬁcation, Image segmentation, Evaluation.

Abstract:

This paper describes the methods of construction and the main characteristics of a solid texture database freely

available for texture classiﬁcation experiment. Here the purpose is to propose a solid texture database with

many classes of different solid textures to allow an evaluation of properties and performance of analysis meth-

ods. Each images is described by a xml ﬁle made according to a DTD which is available in our web site. Using

this formalism, it is even possible for a researcher to propose his own images or creation methods to complete

this solid texture database. At last we discuss about different ways to exploit the database by reviewing some

evaluation methods used to evaluate performance of classiﬁcation and segmentation algorithms.

1 INTRODUCTION

Texture analysis is an important topic of image anal-

ysis and many researchers have attempted to explain

texture perception (Julesz, 1962). Research in this do-

main can be divided in three types of problems includ-

ing texture classiﬁcation, texture segmentation and

texture synthesis. Existing feature extraction tech-

niques can be divided into four categories (Tuceryan

and Jain, 1998) that is to say statistical (Haralick,

1979; Haralick et al., 1973; Ojala et al., 1996), geo-

metrical (Tuceryan and Jain, 1990), frequential (Mal-

lat, 1989) and model based methods (Chellappa and

Jain, 1993; Mosquera et al., 1992). All these meth-

ods have been mainly developed and experimented

on two-dimensional texture images. Recently, some

of these methods have been investigated to analyse

solid texture. A large number of papers including a

solid texture analysis method refer to medical anal-

ysis (Jafari-Khouzani et al., 2004; Showalter et al.,

2006) except in (Suzuki et al., 2004) which use a solid

texture database based on Perlin’s noise functions.

Currently, no comparison between all these methods

are available because they all work on different types

of images. The purpose of this paper is not to pro-

pose texture synthesis methods to obtain solid texture

as realistic as possible but to propose a solid texture

database with many classes to allow an evaluation of

properties and performance of solid texture analysis

methods. In the section 2 we present the different

methods used to generate the database and properties

of each of them. In section 3, we explain the organi-

zation and structure of our database and then section

4 explain different way to exploit it with a review of

current evaluation methods.

2 SYNTHESIS AND PROPERTIES

OF THE SOLID TEXTURE

DATABASE

Solid textures, sometimes called volumetric textures,

are textures represented in three-dimensional space

and can be considered as a two-dimensional texture

images series or as a texture that can be found in a vol-

umetric data. Volumetric texture is different from 3D

Texture or Volumetric Texturing. 3D Texture (Cuba

and Dana, 2004) refers to the observed 2D texture of a

3D object viewed from a particular angle and with dif-

ferent lighting conditions and Volumetric Texturing

(Neyret, 1995) correspond to the rendering of repet-

itive geometries and reﬂectance into voxels. There

are many two-dimensional databases to compare tex-

ture analysis methods and one of the best known is

the Brodatz database (Brodatz, 1966). In (Kopf et al.,

2007), Johannes Kopf et al construct solid textures

from two-dimensional texture images. Some exam-

ples are available

but currently there are too few im-

http://johanneskopf.de/publications/

solid/textures/index.html

135

Paulhac L., Makris P. and Ramel J. (2009).

A SOLID TEXTURE DATABASE FOR SEGMENTATION AND CLASSIFICATION EXPERIMENTS.

In Proceedings of the Fourth International Conference on Computer Vision Theory and Applications, pages 135-141

DOI: 10.5220/0001768401350141

 SciTePress

ages to make a classiﬁcation experiment.

In (Gool et al., 1985), Van Gool et al describe three

classes of texture with deterministic textures, stochas-

tic textures and observable textures. The ﬁrst category

is characterized by the repetition of a geometrical pat-

tern. This kind of texture can be synthesized using a

pattern of speciﬁc size and direction. To the contrary,

stochastic textures are irregular and no repetitive pat-

tern is identiﬁable. At last observable textures can

be deﬁned as a mix between geometric and stochastic

textures. Patterns are very closed but not identical.

To have a complete and representative database, we

have tried to build synthetic images representative of

all these three classes.

To limit necessary disk space and processing time,

each of the volumetric texture images have a size of

. This size seems sufﬁcient to allow classiﬁcation

experiments. The images have been constructed using

four different methods.

With a ﬁrst method, volumetric textured images are

constructed using two-dimensional texture images

like Brodatz textures, fractal textures etc. Two or

more two-dimensionaltexture images are interpolated

to obtain a three dimensional image (Figure 1). It is

important to know that two-dimensional textures used

to build a three-dimensional image are not exactly

similar. With the interpolation, these textures have a

particular direction and evolve regularly. A good ex-

ample of this kind of texture could be a tree bole. An

interpolated texture can be deﬁned as a set of textured

blocks B

built using two-dimensional textures E:

T,i

= E

+ i

− E

T+1

)

(1)

with M = N/(R − 1) the number of two-dimensional

components in a block, N the depth of the solid tex-

ture, R the number of two-dimensional textured im-

ages used to interpolate, T = {0,...,R − 1} and i =

{0,1,...,M − 1}.

The properties of this kind of texture depends on the

chosen two-dimensional texture and the number of in-

terpolation plans.

A second method consists to use geometric shapes

like sphere, cube, ellipsis, etc. With this method it

is possible to construct deterministic texture. A pat-

tern will be a geometric shape allocated in a given

direction. Moreover, observable texture can be easily

generated for example using many sphere with ran-

dom size and random arrangement. To construct a

gruyere texture, we place randomly sphere or ellipsis

with random sizes in a yellow three-dimensional im-

age. The properties of this type of texture depends on

the number of patterns, the shape of the patterns, the

size of patterns which can be ﬁxed or randomly cho-

(a) Two-dimensional textured

images

(b) Volumetric texture by in-

terpolation

Figure 1: Example of construction of an interpolated solid

texture.

sen, and the color which can also take a random or

ﬁxed value. Figure 2 shows two volumetric textures

generated with this method.

(a) Cube Pattern (b) Sphere Pattern

Figure 2: Example of solid textures with geometric shapes.

The third method allows to synthesize solid texture

using Fourier transformation as presented in (Lewis,

1984). For that, it is necessary to construct a power

spectrum in order to specify frequencies that will be

present in the synthesized texture and their amplitude.

It is so possible to paint it with the respect of the quad-

rant symmetry or using powerspectrum from an exist-

ing texture. For the phase spectrum, we can use ran-

dom value or take it from an existing texture. Then,

we are able to synthesize solid textures with an in-

verse Fourier transform using these two components.

Each example of texture in a given class is not exactly

similar. Indeed, examples in a class are made using

a unique power spectrum and a phase spectrum with

some variations. As describe in (Lewis, 1984), this

texture synthesize method is not intuitive, but allows

to construct rich textures difﬁcult to obtain in the spa-

tial domain.

At last, it is also possible to obtain a fourth category

of three-dimensional images using a mix between

the three previous methods. Instead of generate a

pattern with a color like in the second method, we

can create patterns with a given texture using the

VISAPP 2009 - International Conference on Computer Vision Theory and Applications

136

(a) Power Spectrum 1 (b) Texture build with the

ﬁrst power spectrum

second power spectrum

Figure 3: Example of solid textures build using inverse

Fourier transform.

ﬁrst synthesis method or texture obtained with the

inverse Fourier transform (Figure 4). The textures

so generated contain geometric shapes with a given

texture. Moreover it is possible to insert a texture

outside patterns to obtain a textured background. A

texture like this one is described by the number of

pattern, the shape and the size of patterns, and the

used texture inside and outside patterns.

To complete this database, we apply some trans-

(a) Texture Inside Patterns (b) Texture Inside and Out-

side Patterns

Figure 4: Example of solid textures with texture outside or

inside geometric shapes.

formations on each class of texture with rotations

according x, y and z axis. This is so possible to test if

a texture analysis method is invariant to a given trans-

formation. Moreover, Gaussian noise, Gaussian blur

and sub-sampling are applied to increase variability

in each existing volumetric texture classes (Figure

5). The interest of using these transformations is to

test for example the robustness to noise or blur of an

analysis method and to be able to increase easily the

difﬁculty of the comparison between images of the

database.

Figure 5: [a-c]) Solid textures with random rotation, [d-e]

Two blurry textures, [f-g] Two noisy textures, [h-i] Two sub-

sampled textures.

3 ORGANIZATION OF THE

DATABASE

Our database is now available in free access

and

it is so possible to evaluate volumetric texture anal-

ysis methods with classiﬁcation experiments or with

segmentation problems. The database is organized as

follow: each textured images are allocated accord-

ing to the synthesis method that is to say their are

partitioned in four folders. In each folder of texture

synthesize type, images are assigned according to the

applied distortion: nothing, Gaussian blur, Gaussian

noise, rotation or sub sampling. At last, folders of

distortion contain examples of the different classes of

volumetric textures.

Currently, our database contains 95 different classes.

http://www.rfai.li.univ-tours.fr/fr/ressources/

3Dsynthetic_images_database.html

A SOLID TEXTURE DATABASE FOR SEGMENTATION AND CLASSIFICATION EXPERIMENTS

137

30 of these classes have been built with the interpola-

tion method, 25 with the geometrical shape method,

15 with the inverse Fourier transform and 25 with the

blended method. Each class is composed by 50 exam-

ples : 10 blurry textures, 10 noisy textures, 10 textures

with sub sampling distortion, 10 with random rota-

tions and 10 without any transformation. Each volu-

metric image is corresponding to a set of 64 gray level

BMP images of 64 × 64 pixels stored in a speciﬁc di-

rectory. So it is very easy to implement a program

able to load such three-dimensional images. A viewer

is also available on the web site. We choose to make

volumetric textures of size 64

because it is a sufﬁ-

cient size for experiments and this is a good compro-

mise for disk storage. At last, images for segmenta-

tion experiments (images that contain more than one

texture) have a size of 128

that allows a better degree

of freedom to emplace textures.

For each volumetric images, a xml ﬁle is generated

and contains informations about the image tag. The

root of a xml ﬁle is an image which can contain one or

many solid texture descriptors. Indeed, for a texture

recognition problem the used three-dimensional im-

ages correspond to an unique solid texture, whereas a

three-dimensional image contains more than one vol-

umetric texture for a segmentation problem. A solid

texture is deﬁned by a packaging, a name which cor-

respond to the name of a class, the type of synthesis

used, properties and distortions which have been ap-

plied. A packaging is used because in the case of a

segmentation problem, a volumetric texture is not au-

tomatically deﬁned in a cube. Currently, a texture can

be created according to three different shapes (cube,

sphere, ellipsis), with a given size, a given location

and with a particular orientation. Properties depend

on the type of synthesize method used to make a tex-

ture as describe in section 2. For example, a volumet-

ric texture made with inverse Fourier transform de-

pends on the input power spectrum. In order to utilize

these xml ﬁles we made a DTD ﬁle (appendix) which

is available in our web site.

In this section, we describe the structure of our

database. Each images is described by a xml data

and a DTD specify the formalism. Using this DTD,

it is then possible for a researcher to complete this

database with its proper methods or with an existing

one in order to increase the number of classes and

images. Currently the database contains 95 differ-

ent classes which is enough if we compare with ex-

isting two-dimensional databases. For example Bro-

datz database (Brodatz, 1966), which is a standard

for evaluating texture algorithms, has 112 different

classes.

4 EXPLOITATION OF THE

DATABASE

This part is a description of different ways to exploit

our database. We have seen that two types of im-

ages are available: images containing one solid tex-

ture and images with multiple solid textures. Three-

dimensional images with single volumetric texture

can be used to create a classiﬁcation problem. Here

the purpose is that the tested classiﬁcation algorithms

decide which is the class of a texture. Images with

many solid texture allow to test methods for classi-

ﬁcation (a label is attributed to a voxel) or segmen-

tation. Image segmentation and recognition are two

aspects of the same problem: in the ﬁrst case an im-

age is divided into homogeneous zones delimited by

boundaries whereas classiﬁcation consists in labeling

or indexation of components (image,voxel etc.). A

lot of methods have been proposed for the evaluation

of segmentation and classiﬁcation algorithms (Zhang,

1996). Here we will review some of them to explain

how to evaluate an algorithm with our database.

4.1 Classiﬁcation Evaluation

We have seen that the goal of a classiﬁcation method

is to decide the class of a given image. In general,

a classiﬁcation system can be divided in three step.

The ﬁrst one consist to extract features from the im-

ages. In the case of texture problem, it is used clas-

sical algorithms which have been quickly presented

in our introduction (Haralick et al., 1973; Chellappa

and Jain, 1993; Mallat, 1989; Ojala et al., 1996). The

second one consist in a selection of features. This

step allows to reduce the feature space and to keep

the most signiﬁcant features for an application. In

the last one, feature vectors are used to feed classi-

ﬁcation algorithms like for example neural network,

support vector machine, k-nearest neighbors etc. To

classify images with these algorithms, there are two

important stages: a learning phase which uses a learn-

ing database and a test phase which is applied on a

test database. In the ﬁrst phase, a classiﬁcation al-

gorithm learns features which correspond to the dif-

ferent classes and during the second one, we just test

how the classiﬁcation algorithm tags the different im-

ages. To evaluate classiﬁcation systems and compare

their robustness in a given application, a classical ap-

proach is the confusion matrix which represent the

number of elements c

i, j

from the class i classiﬁed in

the class j. The normalized confusion matrix NCM

can be computed as follow:

NCM

i, j

∑

k=1

i,k

(2)

VISAPP 2009 - International Conference on Computer Vision Theory and Applications

138

with T the number of considered classes.

Using this matrix, it is then possible to compute some

measures like:

the true positive rate,

TPrate

= NCM

i,i

(3)

false positive rate,

FPrate

∑

j=1, j6=i

NCM

i, j

(4)

accuracy,

Accuracy =

∑

i=1

NCM

i,i

(5)

error classiﬁcation rates ECR with for example:

ECR =

∑

i=1

0.5(

∑

j=1, j6=i

NCM

i, j

∑

j=1, j6=i

NCM

j,i

T−1

)

(6)

In this error classiﬁcation rate, we consider two errors

with elements from a given class i falsely classiﬁed as

elements of another class and elements classiﬁed in a

given class j but belonging to an other class i.

In (Martin et al., 2006), Martin et al propose an inter-

esting approach which consists to make a confusion

matrix taking into account the inhomogeneous units

and uncertain of the experts. This method can be in-

teresting in the case of natural images which usually

require more than one expert classiﬁcation.

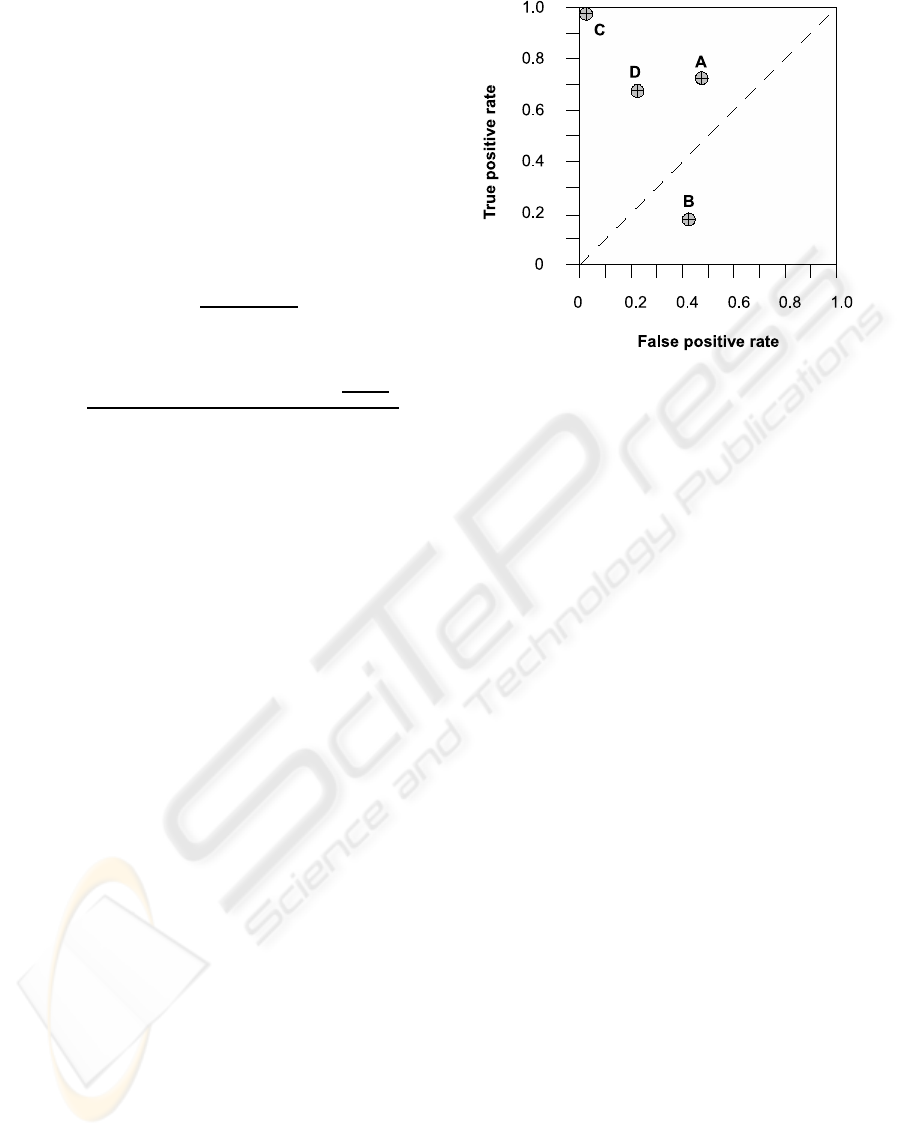
Another way to examine the performance of clas-

siﬁers is to use a receiver operating characteristics

(ROC) graph which is a technique for visualizing and

selecting classiﬁers based on their performance. ROC

graphs are two-dimensional graphs where Y axis rep-

resents TPrate (formula 3) and where FPrate (for-

mula 4) is plotted on the X axis. For a given class, an

ROC graph describes trades off between true positive

and false positive. Then, if T classes are considered,

it is possible to generate T different ROC graphs. For

each classiﬁer, we can compute a (FPrate,TPrate)

pair that allows to compare their performance (Figure

6). The point (0,1) which correspond to C classiﬁer

represents perfect classiﬁcation. For more informa-

tion about ROC analysis, Fawcett in (Fawcett, 2006)

presents a guide for using them in research in order to

promote better evaluation practices.

Their exist several measure to evaluate classiﬁcation

problems. In (Ferri et al., 2008), Ferri et al describe

and study the relationships between the most common

performance measures for classiﬁers. They conclude

about the existence of important similarities between

measures but also signiﬁcant differences between oth-

ers.

Figure 6: Example of an ROC graph.

4.2 Segmentation Evaluation

As explain in (Martin et al., 2006), method like con-

fusion matrix allows only an evaluation of the classi-

ﬁcation approach but does not give an evaluation of

the produced segmentation. Segmentation evaluation

can not be made by visual comparison but using some

metrics. Some methods have been proposed and can

be classiﬁed in two families: supervised evaluation

methods that require access to a ground truth refer-

ence and unsupervised evaluation methods that do not

have an a priori knowledge of the correct segmenta-

tion.

Supervised evaluation methods measure the degree of

similarity between expert and machine segmentation.

The main advantage of this kind of methods is that

they allows to obtain a veryﬁne resolution of the eval-

uation. Nevertheless, generate a ground truth can be

difﬁcult and cost a lot of time. It is not the case with

our database. Indeed segmented images are avail-

able and it is easy to construct them using informa-

tions in xml ﬁles (ﬁgure 7). To evaluate a segmenta-

tion, it is necessary to take into account different pos-

sible errors: under-segmentation where components

are missing, over-segmentation which correspond to

an addition of pixel in a contour, and localisation er-

rors. In (Chabrier et al., 2008), Chabrier et al pro-

pose a comparative study of 14 supervised evalua-

tion criteria according to several degradations (under-

segmentation, over-segmentation etc.). Their conclu-

sion is that the Pratt criterion is the most effective and

allows more discriminated results.

Unsupervised evaluation methods are quantitative

and objective evaluation and require no reference

image. These kind of method are very interesting

A SOLID TEXTURE DATABASE FOR SEGMENTATION AND CLASSIFICATION EXPERIMENTS

139

(a) Original image

(b) Uniform region (c) Corresponding bound-

aries

Figure 7: Example of a three-dimensional image with three

solid textures and its corresponding ground truth.

because for many applications it is sometimes im-

possible or very difﬁcult to provide a reference im-

age. For example generate a ground truth for three-

dimensional ultrasound images is a problem because

of their complexity and the third dimension. A lot of

metrics have been presented and some of them pro-

pose for example to measure intra-region uniformity,

inter-region disparity, the shape etc. In (Zhang et al.,

2008), Zhang et al propose a survey of these unsu-

pervised methods and present experiments to evaluate

them along different situations.

5 CONCLUSIONS

In this paper, we propose a solid texture database for

the evaluation and comparison of volumetric texture

classiﬁcation and segmentation methods. Different

approaches have been used to obtain images with a

wide variety of textures. The ﬁrst method makes solid

textures by interpolating two-dimensional images, the

second method by using geometric shapes like sphere,

ellipsis or cube, the third one by applying the inverse

Fourier transform to a given power spectrum and the

last one by generatingshapes with a particular texture.

Furthermore, different sets of images have been pro-

duced by adding different types of distortions. Two

types of images are available: images with one solid

texture and images with multiple solid textures. Each

of them is described by a xml data and a DTD spec-

ify the formalism. It is then possible for a researcher

to complete this database with other methods. At last,

we explain different ways to exploit our database with

a description of common evaluation methods.

Currently, this database is in free access and it is pos-

sible to test texture analysis methods for classiﬁcation

and segmentation purpose. At last it could be interest-

ing to complete this database and provide some natu-

ral images like three-dimensional medical images.

REFERENCES

Brodatz, P. (1966). Textures: A Photographic Album for

Artists and Designer. Dover Pub.

Chabrier, S., Laurent, H., Rosenberger, C., and Emile,

B. (2008). Comparative study of contour detection

evaluation criteria based on dissimilarity measures.

EURASIP Journal on Image and Video Processing,

2008:13 pages.

Chellappa, R. and Jain, A. K. (1993). Markov Random

Fields Theory and Application. Academic Press.

Cuba, O. and Dana, K. (2004). 3d texture recognition using

bidirectional feature histograms. International jour-

nal of Computer Vision, 59(1):33–60.

Fawcett, T. (2006). An introduction to roc analysis. Pattern

Recognition Letters, 27:861–874.

Ferri, C., Orallo, J. H., and Modroiu, R. (2008). An ex-

perimental comparison of performance measures for

classiﬁcation. Pattern Recognition Letters.

Gool, L. J. V., Dewaele, P., and Oosterlinck, A. (1985). Tex-

ture analysis anno 1983. Computer Vision, Graphics,

and Image Processing, 29(3):336–357.

Haralick, R. M. (1979). Statistical and structural approaches

to textures. Proceedings of the IEEE, 67(5):786–804.

Haralick, R. M., Shanmugam, K., and Dinstein, I. (1973).

Texture features for image classiﬁcation. IEEE Trans-

actions on Systems, Man and Cybernetics, 3(6):610–

621.

Jafari-Khouzani, K., Soltanian-Zadeh, H., Elisevich, K.,

and Patel, S. (2004). Comparison of 2d and 3d wavelet

features for tle lateralization. In Proceedings of the

SPIE, volume 5369.

Julesz, B. (1962). Visual pattern recognition. IEEE Trans-

action on Information Theroy, 8.

Kopf, J., Fu, C.-W., Cohen-Or, D., Deussen, O., Lischinski,

D., and Wong, T.-T. (2007). Solid texture synthesis

from 2d exemplars. In SIGGRAPH ’07: Proceedings

of the 34th International Conference and Exhibition

on Computer Graphics and Interactive Techniques.

Lewis, J.-P. (1984). Texture synthesis for digital painting.

SIGGRAPH Computer Graphics, 18(3):245–252.

Mallat, S. G. (1989). A theory for multiresolution signal de-

composition: the wavelet representation. IEEE trans-

action on Pattern Analysis and Machine Intelligence,

11:674–693.

VISAPP 2009 - International Conference on Computer Vision Theory and Applications

140

Martin, A., Laanaya, H., and Arnold-Bos, A. (2006). Eval-

uation for uncertain image classiﬁcation and segmen-

tation. Pattern Recogn., 39(11):1987–1995.

Mosquera, A., Cabello, D., Carreira, M., and Penedo, M.

(1992). A fractal-based approach to texture segmen-

tation. In ICIPA ’92: Proceedings on the International

Conference on Image Processing and its Application.

Neyret, F. (1995). A general and multiscale model for volu-

metric textures. In Davis, W. A. and Prusinkiewicz,

P., editors, Graphics Interface ’95, pages 83–91.

Canadian Information Processing Society, Canadian

Human-Computer Communications Society. ISBN 0-

9695338-4-5.

Ojala, T., Pietikainen, M., and Harwood, D. (1996). A com-

parative study of texture measures with classiﬁcation

based on feature distributions. Pattern Recognition,

29(1):51–59.

Showalter, C., Clymer, B. D., Richmond, B., and Powell,

K. (2006). Three-dimensional texture analysis of can-

cellous bone cores evaluated at clinical ct resolutions.

Osteoporos International, 17:259–266.

Suzuki, M. T., Yoshitomo, Y., Osawa, N., and Sugimoto, Y.

(2004). Classiﬁcation of solid textures using 3d mask

patterns. In ICSMC ’04: International Conference on

Systems, Man and Cybernetics.

Tuceryan, M. and Jain, A. K. (1990). Texture segmentation

using voronoi polygons. IEEE Transactions On Pat-

tern Analysis And Machine Intelligence, 12:211–216.

Tuceryan, M. and Jain, A. K. (1998). Texture Analysis,

chapter 2.1, pages 207–248. The Handbook of Pat-

tern Recognition and Computer Vision.

Zhang, H., Fritts, J. E., and Goldman, S. A. (2008). Image

segmentation evaluation: A survey of unsupervised

methods. Computer Vision and Image Understanding,

110:260–280.

Zhang, Y. (1996). A survey on evaluation methods for im-

age segmentation. Pattern Recognition, 29(8):1335–

1346.

APPENDIX

In this appendix we present the main components of

our DTD. To obtain the complete DTD, it is possible

to download it using our website.

<!ELEMENT Image3D (Author,(SolidTexture+))>

<!ELEMENT Author (♯ PCDATA)>

<!ELEMENT SolidTexture (Packaging,Name,

SynthesisType,Properties,Distortion)>

————————————————————–

<!ELEMENT Packaging (Type,Size,Location,

Rotation)>

...

————————————————————–

<!ELEMENT Name (♯ PCDATA)>

————————————————————–

<!ELEMENT SynthesisType (♯ PCDATA)>

————————————————————–

<!ELEMENT Properties ((TextureModuleName)|

(Pattern,Size,GrayLevel,PatternTexture)|(Texture2D))>

<!ELEMENT TextureModuleName (♯PCDATA)>

<!ELEMENT Pattern (PatternNumber,

PatternShape)>

...

<!ELEMENT Size (Radius1Min,Radius2Min,

Radius3Min,Radius1Max,Radius2Max,Radius3Max)>

...

<!ELEMENT GrayLevel (GrayLevelMin,

GrayLevelMax)>

...

<!ELEMENT PatternTexture (InnerTexture,

OuterTexture)>

...

<!ELEMENT Texture2D (Name,PlanNumber)>

...

————————————————————–

<!ELEMENT Distortion (GaussianSmooth,

GaussianNoise,SubSampling,Rotation)>

...

————————————————————–

A SOLID TEXTURE DATABASE FOR SEGMENTATION AND CLASSIFICATION EXPERIMENTS

141